Для чего используются графики в экономике
Для чего используются графики в экономике
4.1.1. Что такое Экономика.
Микроэкономика изучает функционирование отдельно взятого предприятия; макроэкономика исследует экономику в целом.
4.1.2. Использование графиков в экономике.
Приведем данные в таблице:
| Цена за кг. яблок (в руб.) | Потребление яблок (в кг. за неделю) |
| 3 | 3 |
| 6 | 2 |
| 9 | 1 |
| 12 | 0,5 |
4.1.3. Производство, развитие и торговля.
4.1.4. Спрос и предложение.
Вы можете поработать с учебной моделю, которая демонстрирует понятие предложения.
4.1.5. Эластичность спроса.
Степень ценовой эластичности или неэластичности спроса измеряется при помощи коэффициента Ed, вычисляемого по формуле:
| Ed = | процентное изменение количества спрашиваемой продукции |
| процентное изменение цены |
Вы можете поработать со специальной учебная моделью, которая демонстрирует эластичность спроса.
Также Вы можете поработать с программой, которая показывает зависимость между выручкой и кривой спроса.
Графики в экономике

В этой статье мы разберем такой математический инструмент как график. И поймем, как он используется в экономике, и для чего.
Помните, что такое декартова система координат? Это две перпендикулярные оси (которые называются системой координат), с помощью которых можно определить точное местонахождение любой точки на плоскости. Каждая точка на такой плоскости имеет две координаты – координату на вертикальной оси и координату на оси горизонтальной. Поэтому в такой системе можно легко задавать соответствие между двумя величинами.
Что дают нам графики? Первое, понять зависимость одно фактора от другого. А понимая зависимости мы можем установить точную взаимосвязь между ними и показать их количественные изменения. Ничего не понятно?!) Опять это научный язык?!) Ну, тогда начнем с примеров! Здесь вы точно все поймете! А если будут вопросы, смело задавайте их в комментариях!
Это простой математический пример графика функции у=х. По вертикальной оси расположена зависимая (функция) величина (у), а по горизонтали независимая (аргумент) величина (х). Какое значение примет независимая величина (х), ей будет соответствовать единственное значение зависимой величины (у). На графике видно, что если взять значении 0,1 на оси абсцисс, то на оси ординат значение принимает 10. Если вести от точки 0,1 до точки 10, то там окажется точка их соприкосновения. Вот это точка и есть точка координат. И имеет она два значения (х; у), где первая координата (х) представляет независимую величину, а вторая (у) зависимую величину. И дальше все просто. Увеличивая значение аргумента, мы получаем единственное соответствующее ему значение функции. Т.е. при х=0,2 мы получаем у=20, и так далее… Эта функция называется прямо пропорциональной. При увеличении одной переменной, растет и другая, при уменьшении аналогично, но в сторону уменьшения.
Теперь разберем это на конкретном примере. На примере спроса в экономике. Возьмем данные цены и объема спроса. И обозначим их на нашем графике соответственно точками.
Итак, на вертикальной оси мы отложили цену, а на горизонтальной спрос. Зависимость спроса от цены называется функцией спроса Qd = f ( P ), где Q – это спрос, а P – цена. Спрос выражается в количестве (кг, штук), цена в денежной единице (рубли, доллары, евро).
На вертикальной оси мы отметили две точки (цены) P 1 и Р2 это две цены. На горизонтальной оси мы отметили также две точки Q 1 и Q 2 – это спрос. Точке P 1 соответствует значение точки Q 1, а точке P 2 соответствует значение точки Q 2. Таким образом, мы пришли к тому, что каждому значению точек на вертикальной оси соответствует единственное значение точек на горизонтальной оси. Но это все математика, скажете вы! И будете правы. А теперь мы перейдем к экономике. Мы применим математические знания о функциях и графиках к экономике. Продемонстрируем это на всем известном явлении в экономике, явлении спроса.
Что показывает нам график? Он показывает, что при цене P 2 люди готовы покупать товар в количестве Q 1. А при цене P 2 люди готовы покупать товар в количестве Q 2. Как мы видим, при цене P 2 спрос на товар больше, чем при цене P 1. И это естественно, чем ниже цена, тем более привлекателен товар для приобретения, и чем выше цена, тем менее он привлекателен. Обозначив эти две точки на графике, и соединив их линией, мы получаем график. Это график в экономике называется графиком спроса. И показывает он зависимость величины спроса от цены. И зависимость это обратно пропорциональная. Растет цена, падает спрос. Падает цена растет спрос. Если брать вместо наших точек конкретные цифры и конкретный спрос на какой-то товар, то мы увидим изменение спроса от цены, но уже в конкретном случае. И чем больше точек мы расположим на графике, тем точнее будет динамика кривой спроса. И тем более детальную картину мы увидим. А линия, соединяющая все точки носит название «кривая спроса».
Джалялов Ремзи, специально для Клуба миллионеров Golden MSN Club®
Электронная библиотека
Графики представляют собой масштабное изображение показателей с помощью геометрических знаков. Благодаря им изучаемый материал становится более доходчивым и понятным. В отличие от табличного материала график позволяет зрительно заметить те закономерности, которые содержит числовая информация. На графике более выразительно прослеживаются тенденции и связи изучаемых показателей.
Рис. 13.1. Сравнение четырех предприятий по уровню производительности труда
В экономическом анализе для графического представления информации в основном используют диаграммы. По своей форме они бывают столбиковыми, линейчатыми, круговыми, кольцевыми, линейными, точечными, цилиндрическими, конусными, пирамидальными, фигурными.
По содержанию различают:
· структурные диаграммы (секторные);
Диаграммы сравнения показывают соотношения разных объектов по какому-либо показателю. Наиболее простыми и наглядными для сравнения величин показателей являются столбиковые и линейчатые диаграммы (рис. 13.1).
Структурные (секторные) диаграммы позволяют выразить состав изучаемых показателей, удельный вес отдельных частей в общей величине показателя. В структурных диаграммах изображение показателя дается в виде разбитых на секторы геометрических фигур (квадратов, кругов, колец), площадь которых берется за 100 или 1. Величина сектора определяется удельным весом части (рис. 13.2). Для отображения одновременно и размера явлений, и их структуры могут использоваться столбиковые и линейчатые диаграммы с накоплением (рис.
Рис. 13.2. Структура экспорта основных видов топлива в 2010 г. по физическому объему
Диаграмма динамики предназначена для изображения изменения явлений за соответствующие промежутки времени. Для этой цели могут использоваться гистограммы, линейные, фигурные графики. Чаще всего используются линейные графики. Динамика на таком графике подается в виде линии, которая характеризует беспрерывность процесса (рис. 13.4).
Линейные графики (графики связи) очень широко используются также при изучении связей между показателями (рис. 13.5).
Графики контроля находят широкое применение при изучении сведений о ходе выполнения плана. В таком случае на графике будут две линии: плановый и фактический уровень показателей за каждый день или другой промежуток времени (рис. 13.6).
Рис. 13.3. Линейная гистограмма структуры
Рис. 13.4. Динамика курса национальной валюты
Рис. 13.5. Влияние стоимости нефти на мировом рынке на сравнительную
эффективность экспорта нефти и переработки нефти внутри страны
Современные компьютерные технологии обработки данных значительно облегчают процесс построения графиков и повышают их качество Задачей аналитика в настоящее время является выбор наиболее наглядной формы графического представления данных.
Рис. 13.6. Выполнение плана отгрузки продукции
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Использование графиков в экономических расчетах
Применение графических построений в экономических расчетах. Основные свойства простейших кривых. Плоскость и прямая в пространстве. Кривые безразличия, потребительского бюджета, производственных возможностей, инвестиционного спроса, Филипса и Лаффера.
| Рубрика | Экономико-математическое моделирование |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 10.01.2012 |
| Размер файла | 202,4 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Линии на плоскости
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению. При этом на функцию F должны быть наложены ограничения так, чтобы, с одной стороны, это уравнение имело бесконечное множество решений и, с другой стороны, чтобы это множество решений не заполняло “куска плоскости”. Важный класс линий составляют те, для которых функция есть многочлен от двух переменных, в этом случае линия, определяемая уравнением, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, cуть прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
. Общее уравнение прямой:
Вектор ортогонален прямой, числа A и B одновременно не равны нулю.
Уравнение принимает вид, если есть точка пересечения прямой с осью.
Нормальное уравнение прямой в координатной форме имеет вид:
Уравнение пучка прямых с центром в точке имеет вид:
Если пучок задается двумя пересекающимися прямыми, то его уравнение имеет вид:
Величина угла между прямыми задается формулой:
Равенство есть необходимое и достаточное условие перпендикулярности прямых.
Для того, чтобы два уравнения
задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:
Уравнения, задают две различные параллельные прямые, если и; прямые пересекаются, если.
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов есть отличные от нуля.
Уравнение окружности с центром в точке и радиусом, равным R:
Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек F1 и F2 (фокусов) есть величина постоянная, равная 2a.
Каноническое (простейшее) уравнение эллипса:
Эллипс, заданный уравнением, симметричен относительно осей координат. Параметры называются полуосями эллипса.
Пусть, тогда фокусы F1 и F2 находятся на оси на расстоянии от начала координат. Отношение называется эксцентриситетом эллипса. Расстояния от точки эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:
Если же, то фокусы находятся на оси,
Если, то эллипс является окружностью с центром в начале координат радиуса.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек F1 и F2 (фокусов) равна по абсолютной величине данному числу 2a.
Каноническое уравнение гиперболы:
Гипербола, у которой, называется равносторонней, ее уравнение, а уравнение асимптот. Гиперболы и называются сопряженными.
Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы имеет два вида:
В обоих случаях и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат.
Парабола y 2 = 2рx имеет фокус и директрису, фокальный радиус-вектор точки на ней.
Парабола имеет фокус и директрису; фокальный радиус-вектор точки параболы равен.
Прямая разбивает плоскость на две полуплоскости. На практике для выяснения того, в какой полуплоскости мы имеем, а в какой, применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой и проверяют, какой знак имеет в этой точке выражение. Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости имеет противоположный знак.
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Плоскость и прямая в пространстве
задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением, которое называется уравнением плоскости.
Вектор ортогональный плоскости, называется нормальным вектором плоскости.
В уравнении коэффициенты одновременно не равны 0. Особые случаи уравнения:
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
1) как линия пересечения двух плоскостей, т.е. системой уравнений:
график кривая экономический
2) двумя своими точками), тогда прямая, через них проходящая, задается уравнениями:
3) точкой е и принадлежащей, и вектором ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения называются каноническими уравнениями прямой.
Вектор называется направляющим вектором прямой.
Параметрические уравнения прямой получим, приравняв каждое из отношений параметру t:
Решая систему как систему линейных уравнений относительно неизвестных, приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой:
От уравнений можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
равносильна системе = x1,; такая прямая перпендикулярна к оси Ох. Система равносильна системе; прямая параллельна оси.
Задача. Довольно часто встает следующая задача. Требуется от общих уравнений прямой перейти к параметрическим, которые в некотором смысле являются более удобными. Рассмотрим, как решить такую задачу.
Для того, чтобы написать параметрические уравнения прямой нужно знать координаты какой-нибудь точки на прямой и координаты направляющего вектора. Как найти координаты точки на прямой, мы уже обсуждали вышеНаправляющий вектор можно найти двумя способами.
Пример 11.4 Прямая задана уравнениями
Требуется написать ее параметрические уравнения.
Теперь, зная точку и направляющий вектор, можно написать параметрические уравнения прямой.
Следующая, часто встречающаяся, задача такая:
Дано уравнение плоскости и уравнения прямой. Требуется найти их точку пересечения.
Так как точка пересечения принадлежит и прямой, и плоскости, то она удовлетворяет и уравнению плоскости, и уравнениям прямой. Поэтому для решения задачи нужно объединить уравнение плоскости и уравнения прямой в одну систему и решить ее.
Решение. Прямая задана каноническими уравнениями. Им соответствует система уравнений:
В результате для нахождения точки пересечения прямой и плоскости получаем систему уравнений
Следующие две задачи связаны с нахождением угла.
Еще одну, более сложную, задачу рассмотрим при конкретных числовых данных.
Решение. Найдем сначала проекцию точки на прямую (рис 2.).
Рис.2. Точки, симметричные относительно прямой
Размещено на Allbest.ru
Подобные документы
Использование методов линейного программирования для целей оптимального распределения ресурсов. Методы математической статистики в экономических расчетах. Прогнозирование экономических показателей методом простого экспоненциального сглаживания.
курсовая работа [976,0 K], добавлен 13.08.2010
Модели распределения доходов. Количественный подход к анализу полезности и спроса. Кривые безразличия, решение задачи об оптимальном выборе потребителя. Функции спроса и коэффициент эластичности. Предельная полезность и предельная норма замещения.
презентация [470,8 K], добавлен 28.04.2013
Модели распределения доходов. Количественный подход к анализу полезности и спроса. Отношение предпочтения и функция полезности. Кривые безразличия, решение задачи оптимального выбора потребителя. Функции спроса, изменение цен и коэффициент эластичности.
курсовая работа [412,7 K], добавлен 11.02.2011
Использование математических методов в сфере управления, в традиционных экономических расчетах при обосновании потребностей в ресурсах, разработке планов и проектов. Основные признаки иерархической системы управления и количественная оценка решений.
контрольная работа [57,0 K], добавлен 21.01.2010
Модели стационарных и нестационарных рядов, их идентификация. Системы эконометрических уравнений, оценка длины периода. Определение и свойства индексов инфляции. Использование потребительской корзины и индексов инфляции в экономических расчетах.
книга [5,0 M], добавлен 19.05.2010
Знакомство с основными видами кривых безразличия и функций предложения. Общая характеристика производственной функции Кобба-Дугласа. Рассмотрение особенностей моделирования покупательского спроса и поведения производителя. Рассмотрение модели Стоуна.
презентация [1,3 M], добавлен 31.10.2016
Целевая функция, экстремальное значение которой нужно найти в условиях экономических возможностей, как показатель эффективности или критерий оптимальности. Оптимальное использование ресурсов и производственных мощностей. Общая идея симплексного метода.
контрольная работа [1,1 M], добавлен 18.05.2015
Как читать графики на бирже
Графики — основа технического анализа при торговле на бирже. Они служат для визуальной оценки тенденций котировок конкретного инструмента, прогноза движения цены и анализа, чьи позиции сильнее — спроса или предложения. О том, как научиться читать графики на бирже, читайте в статье.
Возможности графиков и их комбинаций широко используются во время торговли как уже практикующими инвесторами, так и новичками. Естественно, среди доступных инструментов много тех, которые эффективны только для трейдеров с богатым опытом. Но существуют базовые виды, способные раскрыть информацию об активе без лишних сложностей.
Один из самых востребованных визуальных помощников на биржевом рынке — график движения цен. Выделяют несколько его видов.
Линейные графики. Наиболее простое изображение движения цены, но при этом отражающее только один компонент, которого недостаточно для принятия решений. Бары. Иногда их ещё называют столбиковыми графиками. Информативный визуальный вариант, в котором обозначены главные интересующие показатели — минимальный и максимальный уровень цен за выбранный период времени, цены закрытия и открытия. Японские свечи. Востребованный инструмент, отражающий те же параметры, что и бары, но визуализация у них удобнее. Пункто-цифровой. Другое название — крестики-нолики. Это столбики изменения цены, при этом нолик — падение уровня на заданное количество пунктов, крестик — рост на аналогичное значение. Отчётливо прослеживается направление движения котировки и величина скачка, но при этом нет привязки ко времени. Гистограммы. Не используются отдельно, а дополняют другие графики, показывая объём совершённых торгов. Чем больше высота линий, тем активнее оборот актива на рынке.
Навык чтения графиков — база, необходимая для успешного трейдинга. В техническом анализе наиболее востребованы среди трейдеров линейные, бары и свечные графики. Рассмотрим каждый из них подробнее.
Этот вид графика наиболее простой — по осям времени и цены строится линия, которая отражает величину котировки, закрывающей торговый период. По нему отслеживают общий тренд — растут активы в цене или падают, но принять решение без изучения дополнительной информации нельзя. Оптимальные таймфреймы — от одного дня до квартала.
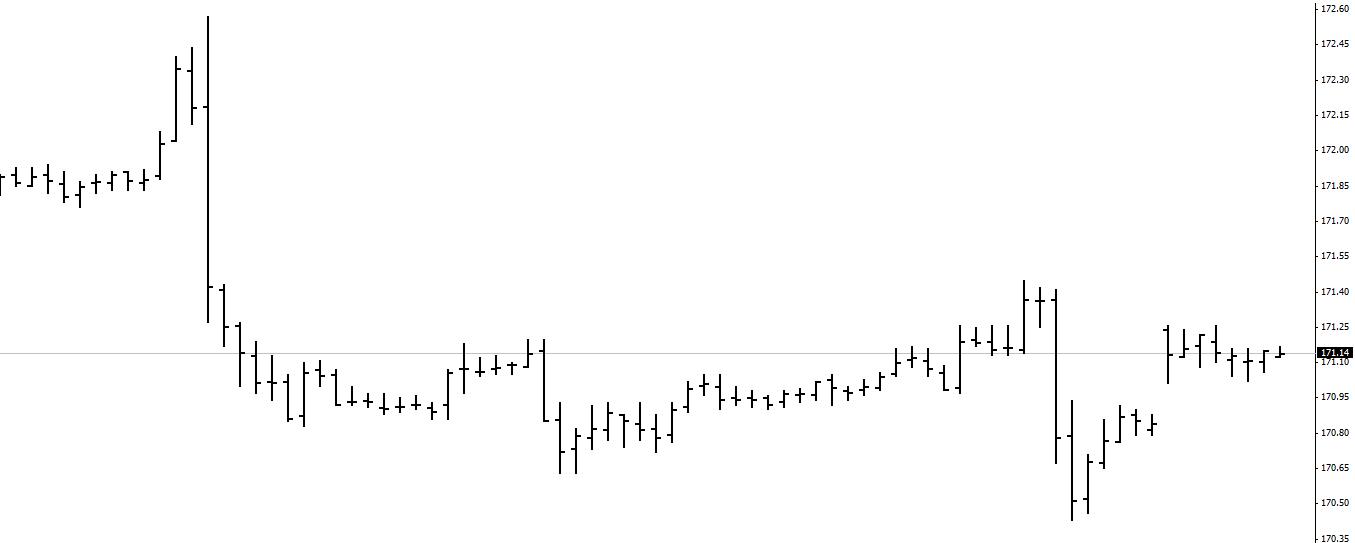
Бары популярны у западных трейдеров. Намного информативнее линейных графиков — посмотреть можно не только цену закрытия, но и открытия, максимальную и минимальную за период торгов.
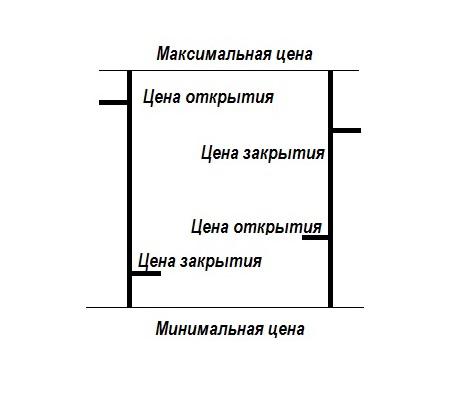
Внешний вид графика — вертикальные столбики с засечками. Границы — это значения минимума и максимума котировки. Засечка слева — цена открытия, засечка справа — цена закрытия. Просмотреть точные цифры можно, наведя курсор мыши на интересующую часть графика.
Каждый столбик — колебания котировки за выбранный таймфрейм. Это может быть пять минут, один час, один день. По окончании очередного периода формируется новая линия. Расположение засечек говорит о направлении движения цены: если левая выше правой, идёт падение, если наоборот — рост.
Такие графики также позволяют понять общую тенденцию и спрогнозировать разворот цены. Например, в ожидании экономических или политических новостей диапазон колебаний котировки уменьшается — столбики становятся короче, рынок замирает. Значимое увеличение длины столбца в сторону минимума или максимума от засечки сигнализирует о возможном развороте движения стоимости в противоположную сторону.
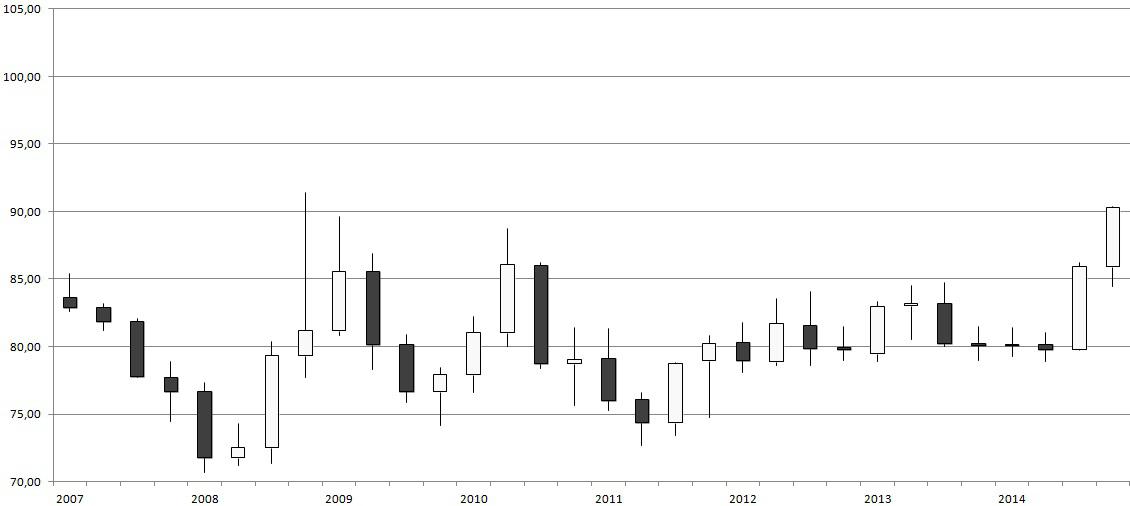
Большинство трейдеров на бирже использует график японские свечи. Он проверен временем — впервые свечные графики стали использовать торговцы при продаже риса ещё в XVII веке. За три сотни лет поклонники появились во всём мире, и их число только растёт.
График состоит из прямоугольников с хвостиками — тела свечи и её тени. Каждый отдельный элемент — это колебания котировки за определённый период времени. Таймфрейм устанавливает пользователь в настройках. Как и в случае с барами, с началом нового промежутка формируется очередная свеча.
Для анализа доступны данные аналогичные барам. Но визуально свечи воспринимаются легче из-за контрастного окрашивания их тел в случае роста и падения цены. В базовом варианте чёрный цвет — стоимость котировки убывает, белый — растёт. Трейдер может выбрать другие оттенки, перейдя в настройки торгового терминала.
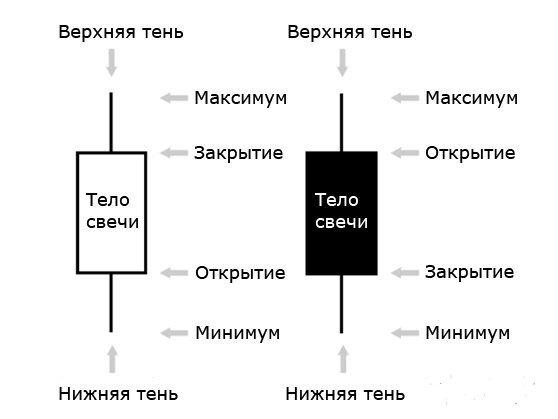
Чтобы разобраться, как читать свечной график на бирже, необходимо познакомиться с каждым элементом. Доступные для анализа параметры имеют собственные обозначения:
open (О) — цена открытия; close © — цена закрытия; low (L) — минимальное значение котировки; high (H) — максимальное значение котировки.
В зависимости от уровня колебаний тело свечи и её тени могут быть разными. Каждая модель носит своё название, например, «молот», «надгробие», «утренняя звезда», и несёт в себе определённый сигнал о ситуации на рынке. Их используют для прогнозирования двух важных состояний торгов:
Чаще всего удлинение тени свечи в сторону минимума характерно для поворота цены в направлении роста, соответственно, увеличение тени в сторону максимума говорит об обратной ситуации.
В любом инструменте есть свои положительные и отрицательные моменты. Предлагаем сравнить основные характеристики базовых графиков в таблице.