Для чего используются графы
Для чего используются графы
Исследовательские работы и проекты
Применение графов в различных областях жизни людей
Глава 2. Возможности применения теории графов в различных областях повседневной жизни
2.1. Применение графов в различных областях жизни людей
Как уже было сказано, графы имеют очень широкое применение: с их помощью выбирают наиболее выгодное расположение зданий, графами представлены схемы метро. Далее представлены некоторые примеры применения графов.
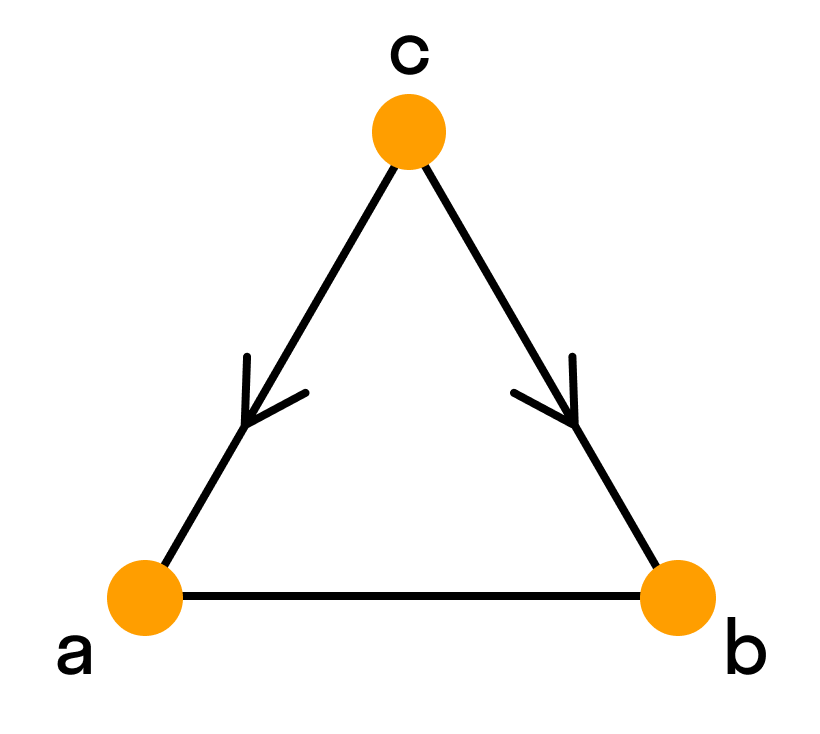
1. Можно составить граф любой позиционной игры: шахмат, шашек, «крестиков – ноликов». 
Здесь позиции станут вершинами, а направленные отрезки между ними будут означать, что одним ходом можно перейти от одной позиции к другой, по направлению стрелки. (приложение 1, рис.1)
Вершинами здесь обозначены тупики, а отрезками – проходы лабиринта. (приложение 1, рис. 2)
3. Генеалогическое древо. 
Граф иерархической системы называется деревом. Отличительной особенностью дерева является то, что между любыми двумя его вершинами существует единственный путь. Дерево не содержит циклов и петель.
Обычно у дерева, представляющего иерархическую систему, выделяется одна главная вершина, которая называется корнем дерева. Каждая вершина дерева (кроме корня) имеет только одного предка – обозначенный ею объект входит в один класс верхнего уровня.
Для каждой пары вершин дерева существует единственный путь, их соединяющий. Этим свойством пользуются при нахождении всех предков, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов. (приложение 1 рис.3).
4. Блок-схема программы 
Графами являются блок – схемы программ для ЭВМ, а так же любые электрические цепи или электрическая сеть.
5. Схема цепей дежурного освещения 
Схема цепей дежурного освещения тепловоза ТЭМ2 тоже представлена в виде графа.
6. Схемы авиалиний 
Схемы авиалиний представлены в виде графов.
Он нарисован тоже в виде графа.
8. Социограммы 
Социограммы (в психологии при исследовании межличностных отношений в группах).
Она тоже представлена с помощью графа.
9. Схема железных дорог 
Схема железных дорог.
Вершины – железнодорожные станции, а рёбра – железнодорожные пути.
10. Созвездия 
Графы есть и на картах звездного неба.
(приложение 1 рис.10).
11. Химия. Теория графов позволяет точно определить и пояснить некоторые основные понятия химии: структуру, конфигурацию, конформацию, квантовомеханическое и статистико-механическое взаимодействия молекул, определять число теоретически возможных изомеров органических соединений, позволяет анализировать некоторые химические превращения, описывать химические реакции, определять некоторые свойства молекул.
12. Математика. Немало поводов для появления графов и в математике. Наиболее очевидный пример – любой многогранник в трёхмерном пространстве.
Так же графы под другими названиями проникли в учебники химии, биологии, географии, где они использованы для наглядного и экономного описания различных схем организаций, логических возможностей, классификаций, в том и только том случае, когда соответствующие круги пересекаются.
13. Физика. Одной из наиболее сложных и утомительных задач для радиолюбителей считается конструирование печатных схем.
Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данного исследования.
Графы и их практическое применение
“ Графы и их практическое применение”.
Ежедневно нам приходится решать различные задачи: математические, экономические, практические, прикладные. Для того чтобы научиться решать задачи, надо разобраться в том, как они устроены, из каких частей ни состоят, каковы инструменты, с помощью которых проводится решение задач. Любая задача представляет собой требование или вопрос, на который надо найти овеет, опираясь и учитывая те условия, которые указаны в задаче. Поэтому, приступая к решению какой-либо задачи, надо внимательнее ее изучить, установить, в чем состоят ее вопросы, требования, каковы условия, исходя из, которых надо решить задачу. Схематическая запись задачи должна быть удобна, компактна, и в то же время, достаточно наглядна. Первой отличительной особенностью схематичной записи задач является широкое использование в ней разного рода обозначения, символов, букв, рисунков, чертежей, схем и т.д. Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики. Графы – замечательные математические объекты, с их помощью можно решать много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применения.
Графы и их практическое применение.
Графы необходимы в использовании во многих областях практической и научной деятельности людей. Например, карты движения метрополитена, маршрутных такси, троллейбусов, автобусов и поездов, генеалогическое древо, карты города, иерархическая структура администрации, таблицы, различные схемы, план дома и график функции. Можно привести много различных примеров, которые объясняют и доказывают, что графы широко распространены в повседневной жизни, и не утратят своей актуальности.
Цель исследования: Исследовать области использования графов и доказать их необходимость в разных сферах жизни людей.
Узнать историю возникновения графов.
Научиться решать задачи с помощью графов.
Познакомиться с видами графов.
(Составить своё родословное).
Объект исследования – графы.
Предмет исследования – практическое использование графов в жизни людей.
Гипотеза исследования – как люди используют графы в своей жизни.
Поисковой метод: изучение научной и публицистической литературы по данному вопросу;
Аналитический метод: анкетирование, сбор материалов и их изучение, составление графиков;
Исследовательский метод: сравнение, сопоставление результатов, анилиз и формулирование выводов
1.1.История возникновения теории графов……………………………………. …5
1.2.Задача о мостах Кенигсберга……………………………………………………5
Графы необходимы в использовании во многих областях практической и научной деятельности людей. Например, карты движения метрополитена, маршрутных такси, троллейбусов, автобусов и поездов, генеалогическое древо, карты города, иерархическая структура администрации, таблицы, различные схемы, план дома и график функции. Можно привести много различных примеров, которые объясняют и доказывают, что графы широко распространены в повседневной жизни, и не утратят своей актуальности.
Цель исследования: Исследовать области использования графов и доказать их необходимость в разных сферах жизни людей.
Узнать историю возникновения графов.
Научиться решать задачи с помощью графов.
Познакомиться с видами графов.
(Составить своё родословное).
Объект исследования – графы.
Предмет исследования – практическое использование графов в жизни людей.
Гипотеза исследования – как люди используют графы в своей жизни.
Поисковой метод: изучение научной и публицистической литературы по данному вопросу;
Аналитический метод: анкетирование, сбор материалов и их изучение, составление графиков;
Исследовательский метод: сравнение, сопоставление результатов, анализ и формулирование выводов.
1.1.История возникновения теории графов.
1.2.Задача о мостах Кенигсберга.
Издавна среди жителей Кёнигсберга (Калининград) была распространена такая загадка: как пройти по всем городским мостам, не проходя ни по одному из них дважды? Многие пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера.
На упрощённой схеме города ( графе ) мостам соответствуют линии (ребра графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа должно быть чётно. Не может существовать граф, который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Если ровно две вершины графа нечётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой из нечётных вершин и завершить его в другой нечетной вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины (то есть все) — следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
В первенстве классов по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводиться по круговой схеме – каждый из участников играет с каждым из остальных только один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной и Еленой; Борис сыграл с Андреем и Галиной; Виктор с Галиной, Дмитрием и Еленой; Галина с Андреем, Борисом и Виктором; Дмитрий с Виктором; Елена с Андреем и Виктором. Сколько игр проведено к настоящему моменту и сколько ещё осталось?
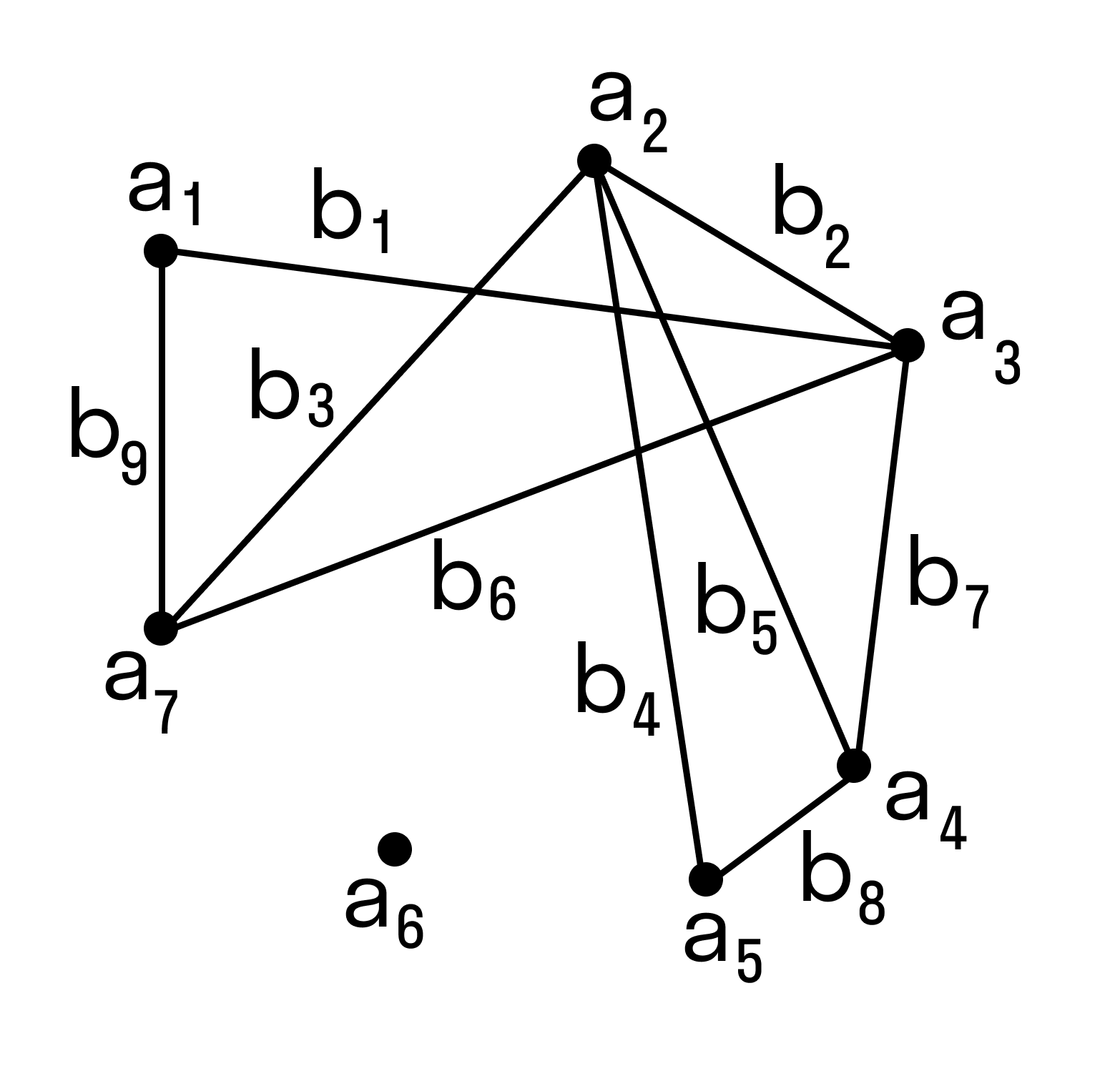
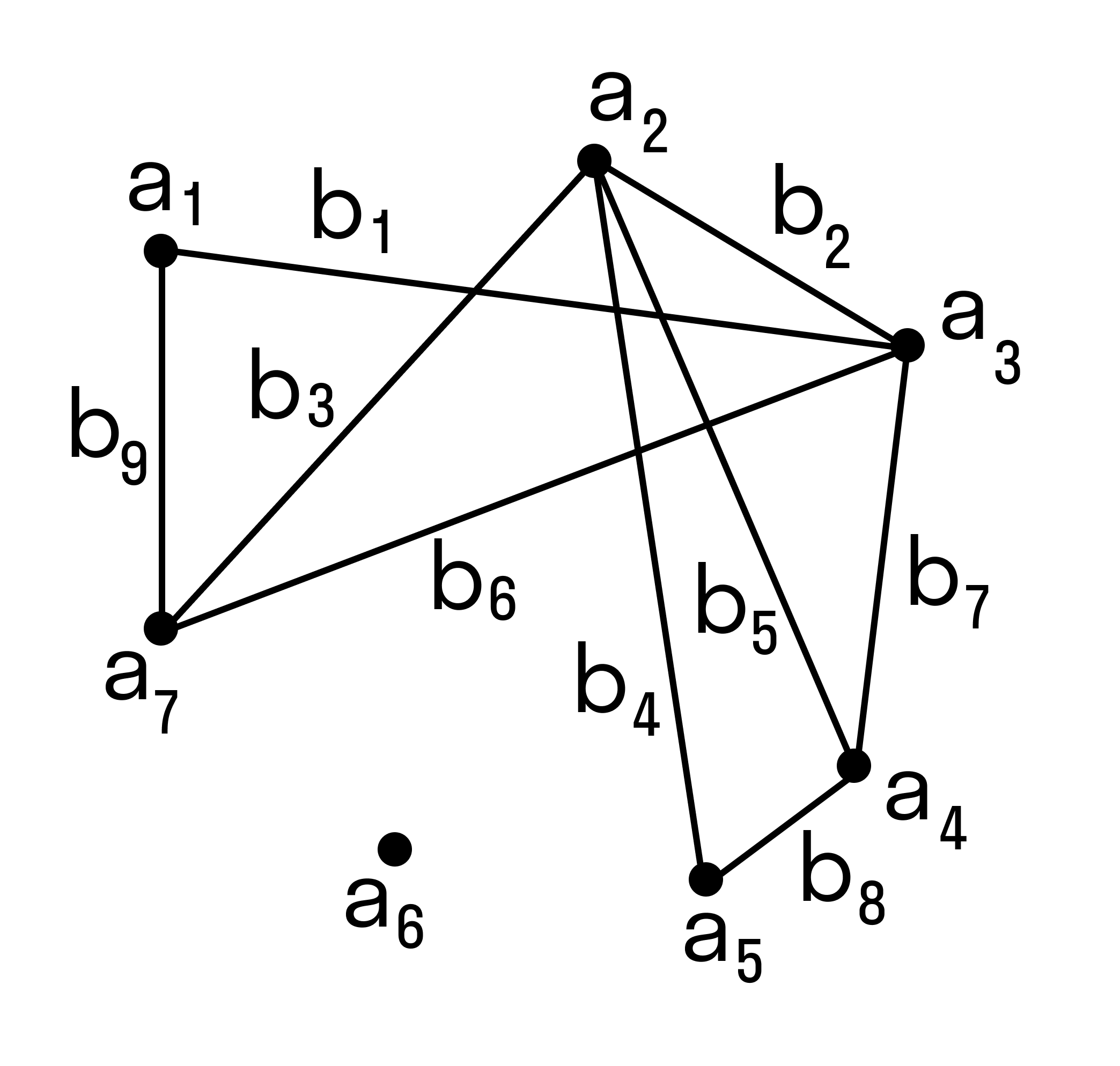
Изобразим данную задачу в виде схемы.
Заметим, что точки пресечения ребер графа не являются его вершинами. Во избежание путаницы вершины графа часто изображают не точками, а маленькими кружочками. Ребра зачастую, оказывается, удобно изображать не прямолинейными отрезками, а криволинейными (дугами).
Вернемся к нашей задаче. Число игр, проведенных к настоящему моменту, равно число ребер, то есть 7. Чтобы найти число игр, которое осталось провести, еще один граф с теми же вершинами, но ребрами будем соединятьтех участников, которые не играли друг с другом.
1.Андрей – Виктор. 5.Борис – Елена.
2.Андрей – Дмитрий. 6.Галина – Дмитрий.
3.Борис – Виктор. 7.Галина – Елена.
4.Борис – Дмитрий. 8.Дмитрий – Елена.
Ребер у этого графа оказалась 8, значит осталось провести 8 игр. При решении текстовых задач необходимые объяснения выполняются в определённой последовательности:
О каком процессе идёт речь?
Какие величины характеризуют этот процесс?
К каким отношениям связаны эти величины?
Сколько различных процессов описываются в задаче?
Есть ли связь между элементами?
Собрание для проведения тайного голосования по важному вопросу избрало четную комиссию, в состав которой вошли: Антонов, Борисов и Ващенко. Члены счетной комиссии должны распределить обязанности: председатель, заместитель, секретарь. Сколькими способами они могут это сделать?
Всего имеется 6 вариантов распределения обязанностей. Чтобы ответить, придется осуществить перебор всех возможных вариантов, или, как чаще говорят, комбинаций. Поэтому подобные задачи называются комбинированными. Просчитывать подобные комбинации в жизни приходится часто. Построим древо возможных вариантов.
Используем кодировку: А – Антонов, Б – Борисова, В – Ващенко; кроме того, порядок расположения букв будет соответствовать распределению функциональных обязанностей: 1 буква – председатель, 2 буква – заместитель, 3 буква – секретарь.
Групповой выбор – раздел теории принятия решений, изучающий концепции и механизмы “справедливого” объединения индивидуальных решений единое
коллективное решение. Различают математическую и психологическую теории группового выбора. В математической теории понятие “справедливый” выбор
определяется с помощью системы аксиом, фиксирующих требований к согласованному решению. В теории группового выбора изучают, как в действительного люди принимают коллективное решение. Рассматривают, в частности, последствия, к которым приводят различные процедуры голосования. Методы теории группового выбора используются для учёта потребительского спроса при планировании производства потребительских товаров, для обработки оценок различными экспертами одного и того же явления и объекта и при согласованном выборе серии взаимосвязей решений.
Дерево – это неориентированный связный граф без циклов. Дерево с n вершинами всегда имеет n ребер. Между любыми двумя вершинами дерева существует единственный маршрут (если его бы не было, нарушилась бы связность, а если бы было два маршрута с одинаковыми концами, то получился бы цикл). Поэтому дерево иногда определяется как минимальный связный граф, то есть граф, в котором удаления любого ребра нарушает связность. Вершина дерева, которая соединена ребром только с одной вершиной, называется висячей вершиной или листом. В любом дереве, содержащем более одной вершины, имеется не менее двух листьев. Ориентированное дерево – это граф с выделенной вершиной (корнем), в котором между корнем и любой вершиной существует единственный путь. При этом возможны два варианта ориентации: либо все пути ориентированы от корней к листьям, либо все пути ориентированы от листьев к корню. Деревья используют в различных математических моделях, связных с информатикой: в теории формальных систем; при описании и проектировании иерархических систем; в задачах планирование; в теории игр где вершины – позиции игры, дуги – ходы, переводящие одну позицию в другую, корень – начальная позиция, листья – заключительная позиция.
Иерархическая структура – это структура системы, части (компоненты) которой связаны отношениями включения или подчинения. Иерархическую структуру имеют предприятия. Аналогично организована административно – территориальная (республика – область – районы – населенный пункт). При этом территории связаны отношениями включения: районы входят в область, а органы управления связаны отношениями подчинения – районы власти подчиняются областным. Армейские соединения (дивизия – полк – батальон – рота – взвод – отделение – солдат) также образуют структуру подобного типа.
Теория графов. Основные понятия и виды графов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Теория графов
В переводе с греческого граф — «пишу», «описываю». В современном мире граф описывает отношения. И наоборот: любое отношение можно описать в виде графа.
Теория графов — обширный раздел дискретной математики, в котором системно изучают свойства графов.
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Давайте на примере.
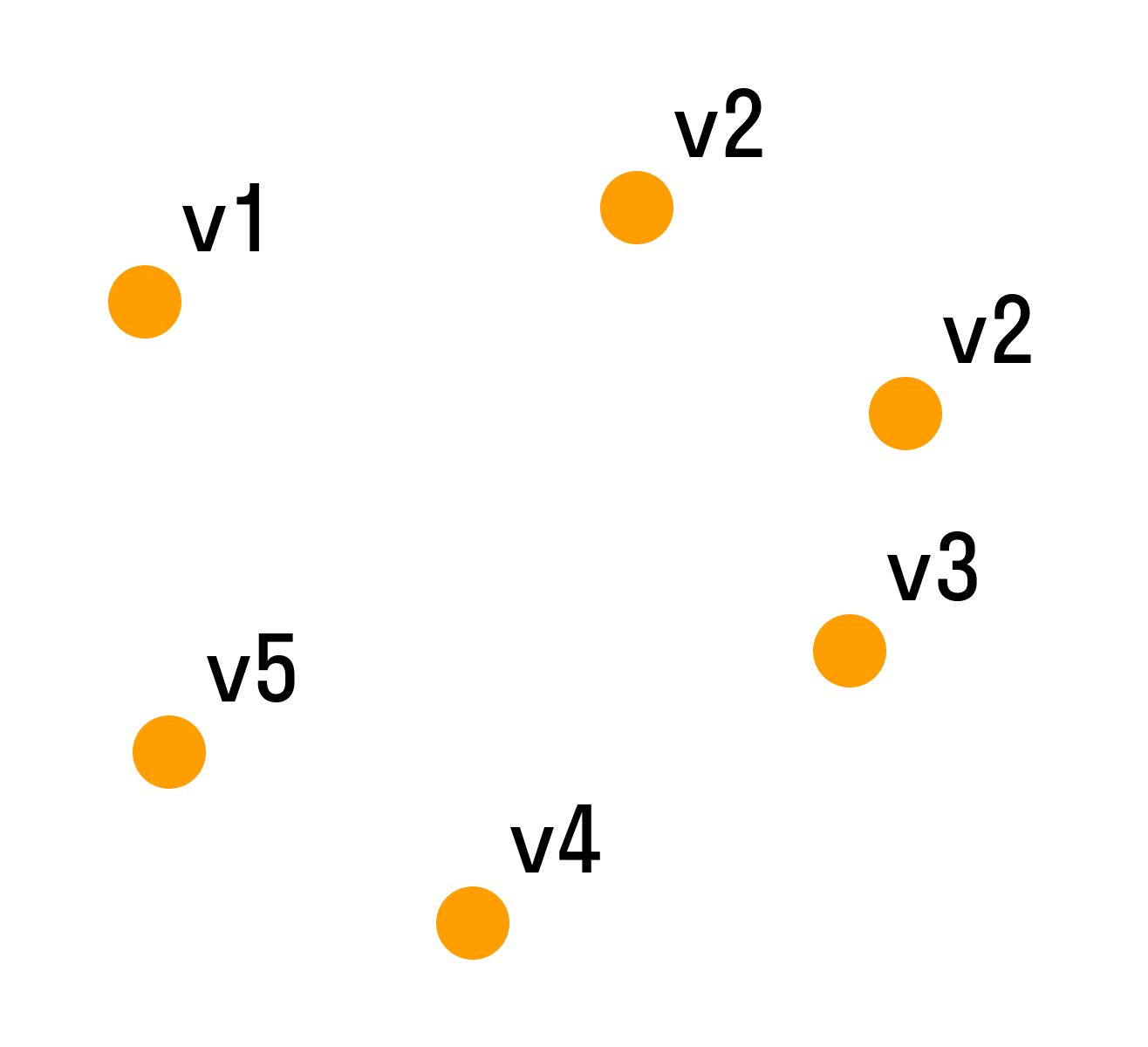
На множестве A зададим отношение знакомства между людьми из этого множества. Строим граф из точек и связок. Связки будут связывать пары людей, знакомых между собой.
Число знакомых у одних людей может отличаться от числа знакомых у других людей, некоторые могут вовсе не быть знакомы (такие элементы будут точками, не соединёнными ни с какой другой). Так получился граф:
В данном случае точки — это вершины графа, а связки — рёбра графа.
Теория графов не учитывает конкретную природу множеств A и B. Существует большое количество разных задач, при решении которых можно временно забыть о содержании множеств и их элементов. Эта специфика не отражается на ходе решения задачи.
Например, вопрос в задаче стоит так: можно ли из точки A добраться до точки E, если двигаться только по соединяющим точки линиям. Когда задача решена, мы получаем решение, верное для любого содержания, которое можно смоделировать в виде графа.
Не удивительно, что теория графов — один из самых востребованных инструментов при создании искусственного интеллекта: ведь искусственный интеллект может обсудить с человеком вопросы отношений, географии или музыки, решения различных задач.
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.
Пусть V — (непустое) множество вершин, элементы v ∈ V — вершины. Граф G = G(V) с множеством вершин V есть некоторое семейство пар вида: e = (a, b), где a, b ∈ V, указывающих, какие вершины остаются соединёнными. Каждая пара e = (a, b) — ребро графа. Множество U — множество ребер e графа. Вершины a и b — концевые точки ребра e.
Широкое применение теории графов в компьютерных науках и информационных технологиях можно объяснить понятием графа как структуры данных. В компьютерных науках и информационных технологиях граф можно описать, как нелинейную структуру данных.
Линейные структуры данных особенны тем, что связывают элементы отношениями по типу «простого соседства». Линейными структурами данных можно назвать массивы, таблицы, списки, очереди, стеки, строки. В нелинейных структурах данных элементы располагаются на различных уровнях иерархии и подразделяются на три вида: исходные, порожденные и подобные.
Основные понятия теории графов
Граф — это геометрическая фигура, которая состоит из точек и линий, которые их соединяют. Точки называют вершинами графа, а линии — ребрами.
Лемма о рукопожатиях
В любом графе сумма степеней всех вершин равна удвоенному числу ребер.
Доказательство леммы о рукопожатиях
Если ребро соединяет две различные вершины графа, то при подсчете суммы степеней вершин мы учтем это ребро дважды.
Если же ребро является петлей — при подсчете суммы степеней вершин мы также учтем его дважды (по определению степени вершины).
Из леммы о рукопожатиях следует: в любом графе число вершин нечетной степени — четно.
Пример 1. В классе 30 человек. Может ли быть так, что у 9 из них есть 3 друга в этом классе, у 11 — 4 друга, а у 10 — 5 друзей? Учесть, что дружбы взаимные.
Если бы это было возможно, то можно было бы нарисовать граф с 30 вершинами, 9 из которых имели бы степень 3, 11 — со степенью 4, 10 — со степенью 5. Однако у такого графа 19 нечетных вершин, что противоречит следствию из леммы о рукопожатиях.
Пример 2. Каждый из 102 учеников одной школы знаком не менее чем с 68 другими. Доказать, что среди них найдутся четверо ребят с одинаковым числом знакомых.
Сначала предположим противоположное. Тогда для каждого числа от 68 до 101 есть не более трех человек с таким числом знакомых. С другой стороны, у нас есть ровно 34 натуральных числа, начиная с 68 и заканчивая 101, а 102 = 34 * 3.
Это значит, что для каждого числа от 68 до 101 есть ровно три человека, имеющих такое число знакомых. Но тогда количество людей, имеющих нечетное число знакомых, нечетно. Противоречие.
Путь и цепь в графе
Путем или цепью в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Циклом называют путь, в котором первая и последняя вершины совпадают.
Путь или цикл называют простым, если ребра в нем не повторяются.
Если в графе любые две вершины соединены путем, то такой граф называется связным.
Можно рассмотреть такое подмножество вершин графа, что каждые две вершины этого подмножества соединены путем, а никакая другая вершина не соединена ни с какой вершиной этого подмножества.
Каждое такое подмножество, вместе со всеми ребрами исходного графа, соединяющими вершины этого подмножества, называется компонентой связности.
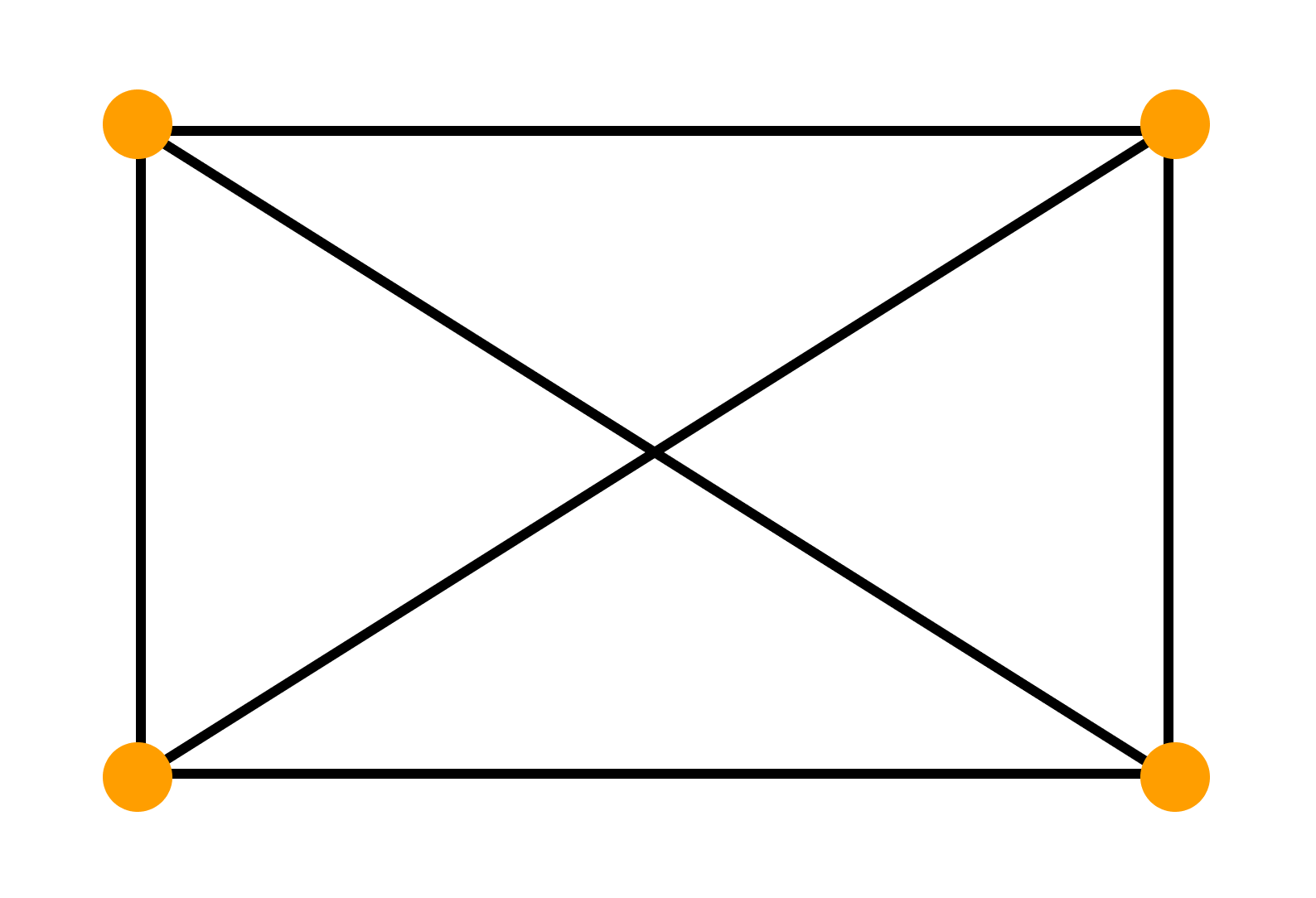
Один и тот же граф можно нарисовать разными способами. Вот, например, два изображения одного и того же графа, которые различаются кривизной:
Два графа называются изоморфными, если у них поровну вершин. При этом вершины каждого графа можно занумеровать числами так, чтобы вершины первого графа были соединены ребром тогда и только тогда, когда соединены ребром соответствующие занумерованные теми же числами вершины второго графа.
Граф H, множество вершин V’ которого является подмножеством вершин V данного графа G и множество рёбер которого является подмножеством рёбер графа G соединяющими вершины из V’ называется подграфом графа G.
Визуализация графовых моделей
Визуализация — это процесс преобразования больших и сложных видов абстрактной информации в интуитивно-понятную визуальную форму. Другими словами, когда мы рисуем то, что нам непонятно — и сразу все встает на свои места.
Графы — и есть помощники в этом деле. Они помогают представить любую информацию, которую можно промоделировать в виде объектов и связей между ними.
Граф можно нарисовать на плоскости или в трехмерном пространстве. Его можно изобразить целиком, частично или иерархически.
Изобразительное соглашение — одно из основных правил, которому должно удовлетворять изображение графа, чтобы быть допустимым. Например, при изображении блок-схемы программы можно использовать соглашение о том, что все вершины должны изображаться прямоугольниками, а дуги — ломаными линиями с вертикальными и горизонтальными звеньями. При этом, конкретный вид соглашения может быть достаточно сложен и включать много деталей.
Виды изобразительных соглашений:
Виды графов
Виды графов можно определять по тому, как их построили или по свойствам вершин или ребер.
Ориентированные и неориентированные графы
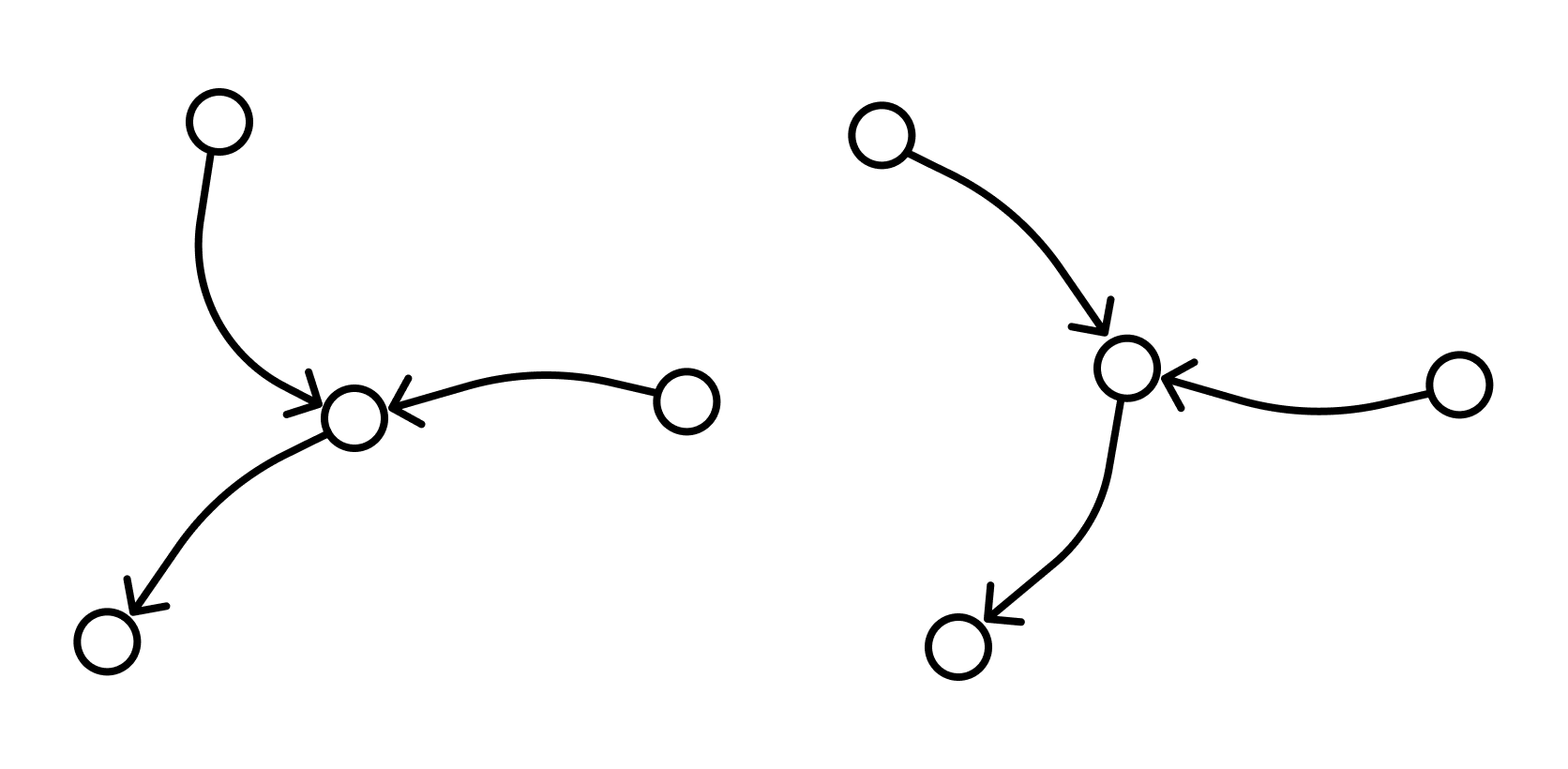
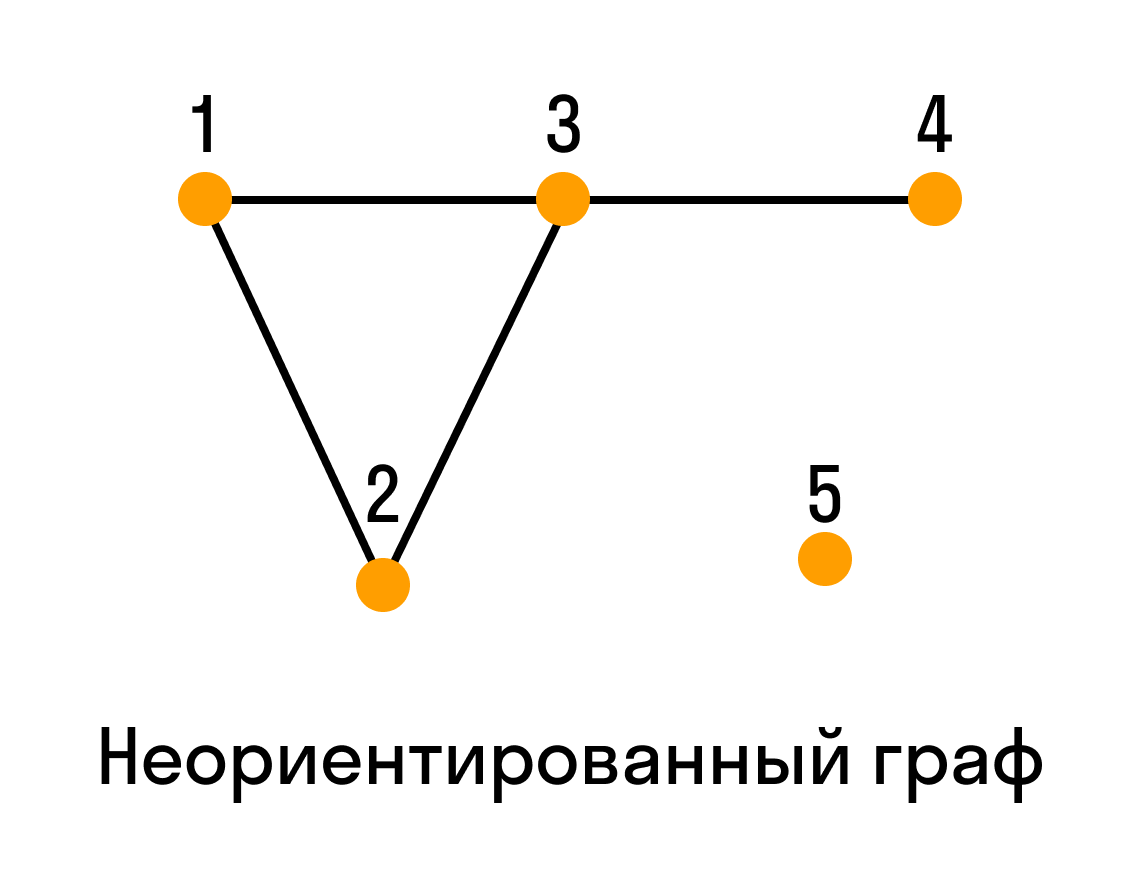
Графы, в которых все ребра являются звеньями, то есть порядок двух концов ребра графа не существенен, называются неориентированными.
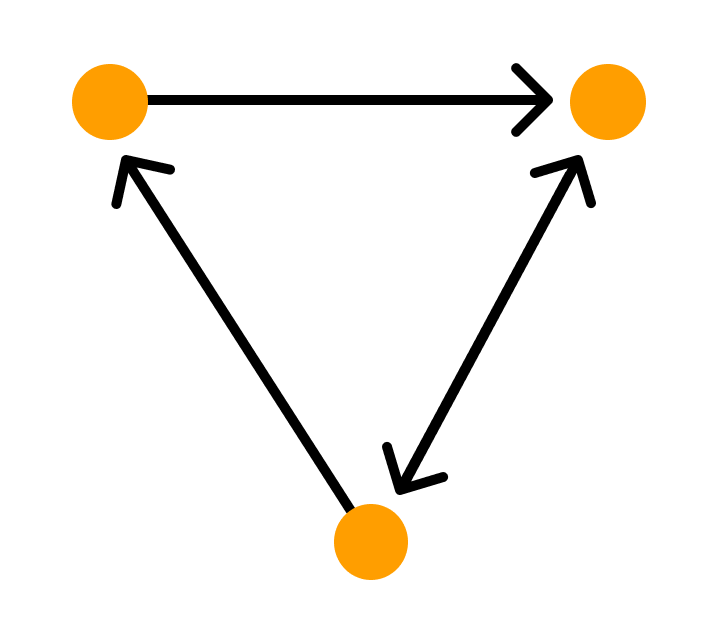
Графы, в которых все ребра являются дугами, то есть порядок двух концов ребра графа существенен, называются ориентированными графами или орграфами.
Неориентированный граф можно представить в виде ориентированного графа, если каждое его звено заменить на две дуги с противоположным направлением.
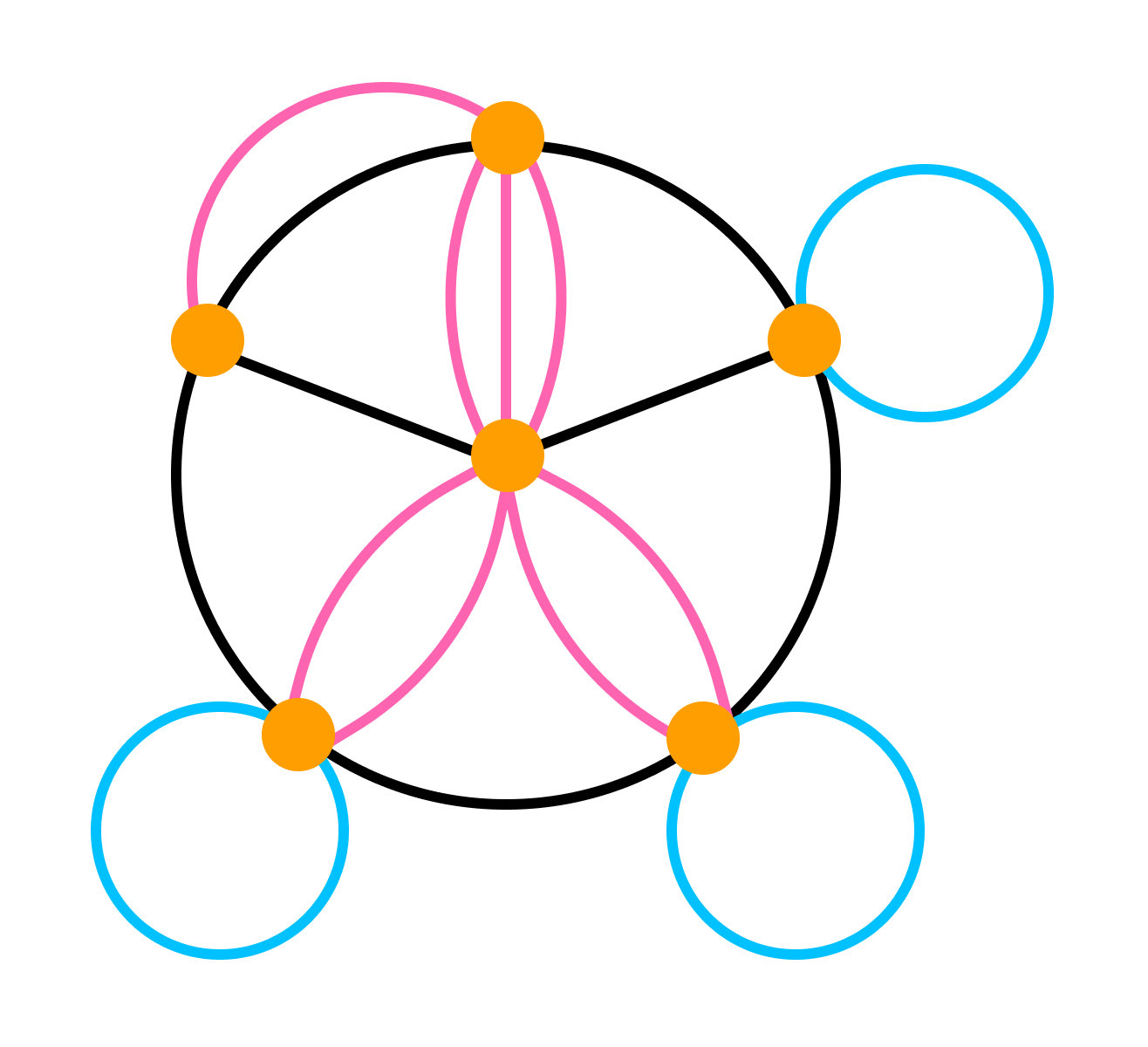
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли — это обстоятельство важно озвучивать и добавлять к основной характеристике графа уточнение «с петлями». Если граф не содержит петель, то добавляют «без петель».
Смешанным называют граф, в котором есть ребра хотя бы двух из упомянутых трех разновидностей (звенья, дуги, петли).
Пустой граф — это тот, что состоит только из голых вершин.
Мультиграфом — такой граф, в котором пары вершин соединены более, чем одним ребром. То есть есть кратные рёбра, но нет петель.
Граф без дуг, то есть неориентированный, без петель и кратных ребер называется обыкновенным.
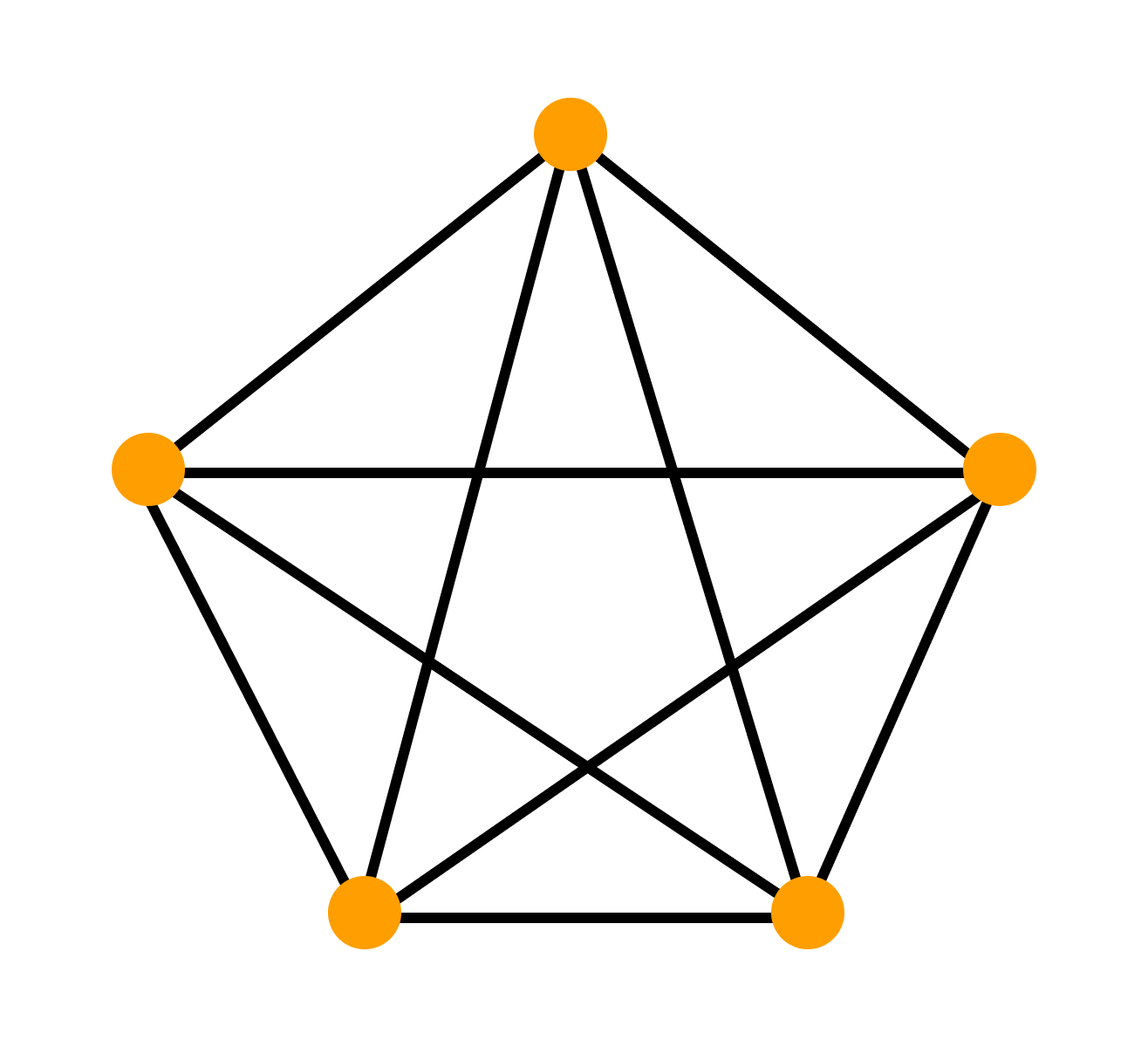
Граф называют полным, если он содержит все возможные для этого типа рёбра при неизменном множестве вершин. Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном.
Двудольный граф
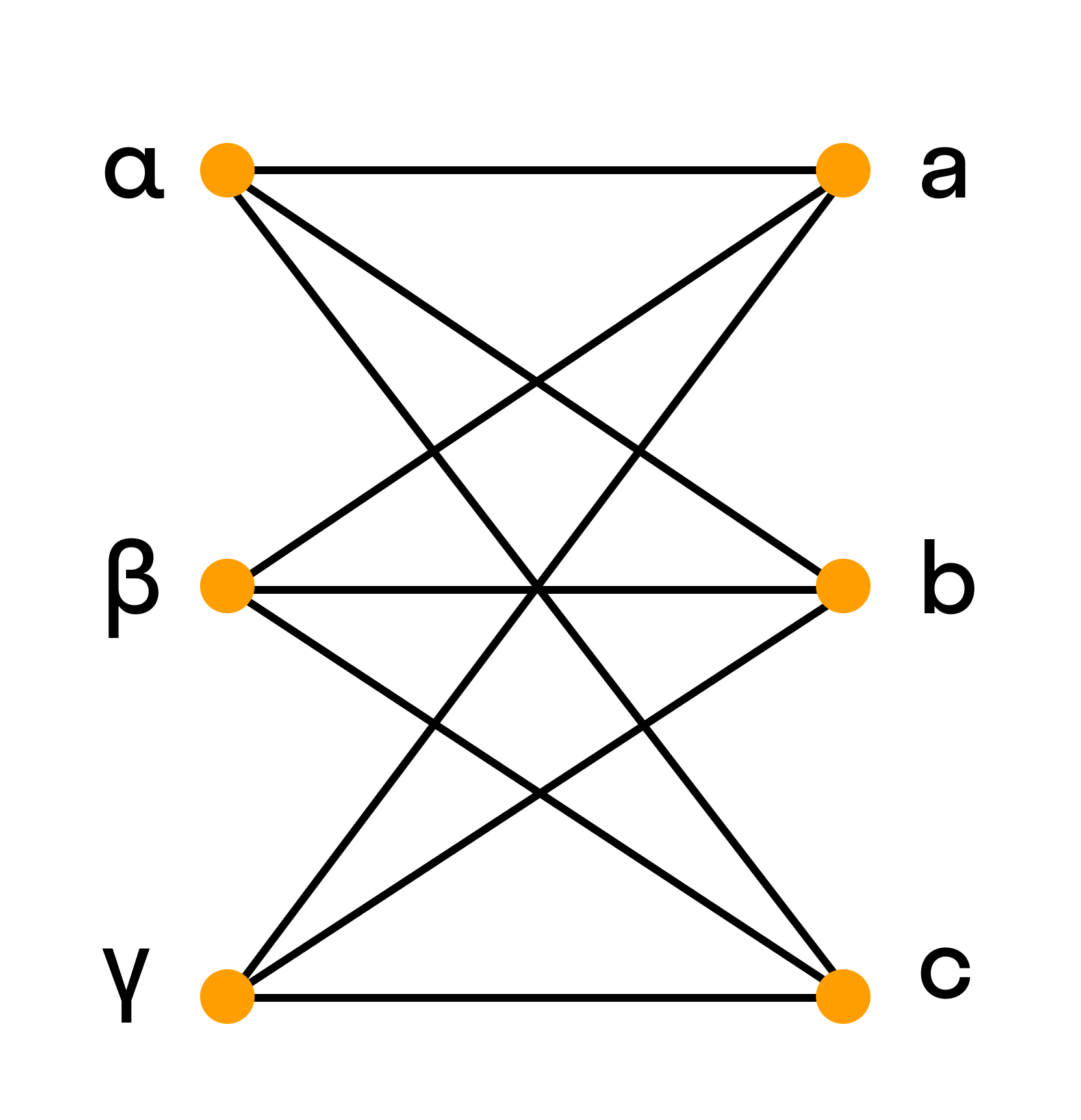
Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.
Например, полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, которые соединяют вершины одного множества с вершинами другого множества.
Эйлеров граф
Эйлеров граф отличен тем, что в нем можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.
Пример. Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом?
Регулярный граф
Регулярным графом называется связный граф, все вершины которого имеют одинаковую степень k.
Число вершин регулярного графа k-й степени не может быть меньше k + 1. У регулярного графа нечётной степени может быть лишь чётное число вершин.
Пример. Построить регулярный граф, в котором самый короткий цикл имеет длину 4.
Чтобы длина цикла соответствовала заданному условию, нужно чтобы число вершин графа было кратно четырем. Если число вершин равно четырём — получится регулярный граф, в котором самый короткий цикл имеет длину 3.
Увеличим число вершин до восьми (следующее кратное четырем число). Соединим вершины ребрами так, чтобы степени вершин были равны трём. Получаем следующий граф, удовлетворяющий условиям задачи:
Гамильтонов граф
Гамильтоновым графом называется граф, содержащий гамильтонов цикл.
Гамильтоновым циклом называется простой цикл, который проходит через все вершины рассматриваемого графа.
Говоря проще, гамильтонов граф — это такой граф, в котором можно обойти все вершины, и каждая вершина при обходе повторяется лишь один раз.
Взвешенный граф
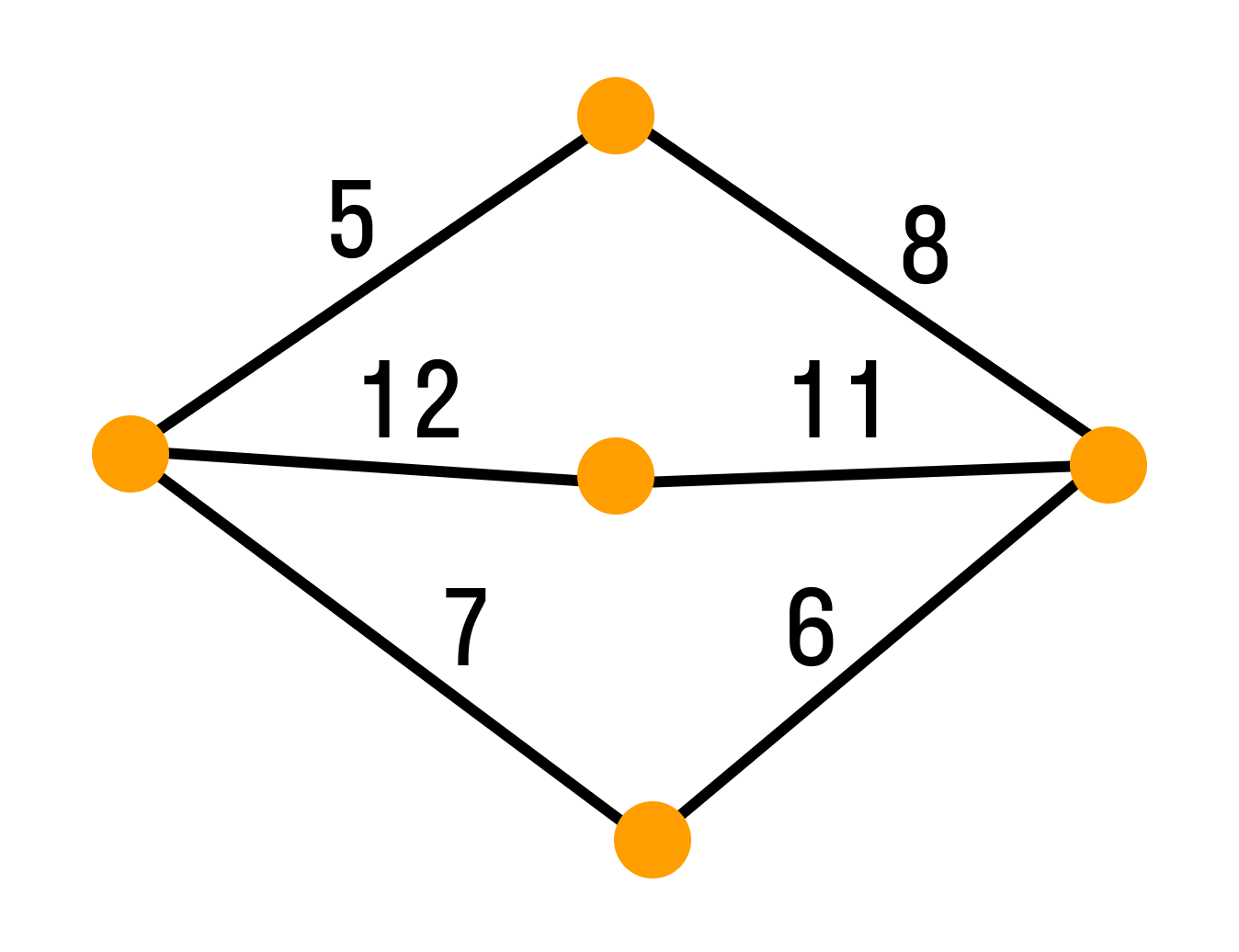
Взвешенным графом называется граф, вершинам и/или ребрам которого присвоены «весы» — обычно некоторые числа. Пример взвешенного графа — транспортная сеть, в которой ребрам присвоены весы: они показывают стоимость перевозки груза по ребру и пропускные способности дуг.
Графы-деревья
Деревом называется связный граф без циклов. Любые две вершины дерева соединены лишь одним маршрутом.
Приведенное соотношение выражает критическое значение числа рёбер дерева, так как, если мы присоединим к дереву ещё одно ребро — будет создан цикл. А если уберем одно ребро, то граф-дерево разделится на две компоненты. Граф, состоящий из компонент дерева, называется лесом.
Определение дерева
Деревом называется связный граф, который не содержит циклов.
Таким образом, в дереве невозможно вернуться в исходную вершину, перемещаясь по ребрам и не проходя по одному ребру два или более раз.
Циклом называется замкнутый путь, который не проходит дважды через одну и ту же вершину.
Простым путем называется путь, в котором никакое ребро не встречается дважды.
Легко проверить, что дерево — это граф, в котором любые две вершины соединены ровно одним простым путем. Если выкинуть любое ребро из дерева, то граф станет несвязным. Поэтому:
Дерево — минимальный по числу рёбер связный граф.
Висячей вершиной называется вершина, из которой выходит ровно одно ребро.
Определения дерева:
Очень часто в дереве выделяется одна вершина, которая называется корнем дерева. Дерево с выделенным корнем называют корневым или подвешенным деревом. Пример: генеалогическое дерево.
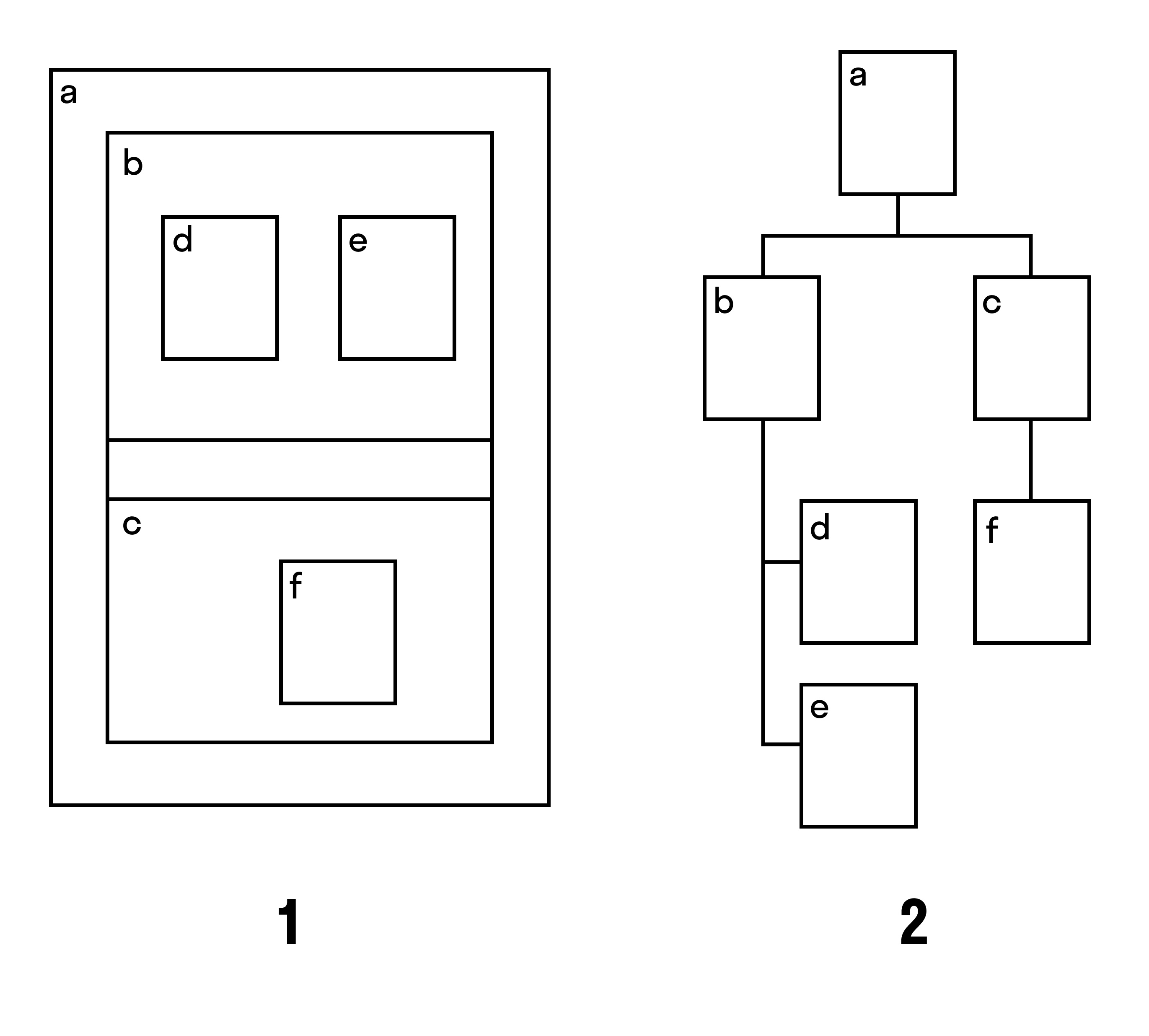
Когда изображают деревья, то часто применяют дополнительные соглашения, эстетические критерии и ограничения.
Например, при соглашении включения (рис. 1) вершины корневого дерева изображают прямоугольниками, а соглашение — опрокидывания (рис. 2) подобно классическому соглашению нисходящего плоского изображения корневого дерева. Вот так могут выглядеть разные изображения одного дерева:
Теоремы дерева и их доказательства
В дереве с более чем одной вершиной есть висячая вершина.
Доказательство первой теоремы:
Пойдем из какой-нибудь вершины по ребрам. Так как в дереве нет циклов, то мы не вернемся в вершину, в которой уже побывали. Если у каждой вершины степень больше 1, то найдется ребро, по которому можно уйти из неё после того, как мы пришли в нее.
Но поскольку количество вершин в дереве конечно, когда-нибудь мы остановимся в некоторой вершине. Противоречие. Значит, когда-нибудь мы дойдём в висячую вершину. Если же начать идти из неё, то мы найдём вторую висячую вершину.
В дереве число вершин на 1 больше числа ребер.
Доказательство второй теоремы:
Докажем по индукции по количеству вершин в дереве n. Если в дерево одна вершина, то факт верен. Предположим, что для всех n