Для чего изучают матрицы
Что такое матрицы, откуда они взялись, и чем они полезны?
Первые упоминания о матрицах или «волшебных квадратах», как их тогда называли, были найдены на территории еще Древнего Китая, однако бум случился намного позже, в середине XVIII века, когда знаменитый математик Габриэль Крамер опубликовал свой труд под названием «Введение в анализ алгебраических кривых», в котором описывался алгоритм решения систем линейных уравнений совершенно новым методом.
Как следствие, в дальнейшем появляются «классический» метод решения Карла Фридриха Гаусса, теорема Гамильтона-Кели, работы Карла Вейерштрасса, Георга Фробениуса и других выдающихся ученых.
Занимательно, что только после всех этих открытий, а именно в 1850 году был непосредственно введен термин матрица, автором которого стал Джеймс Джозеф Сильвестр.
Сегодня термин «матрица» применяется во множестве разных областей: от программирования до кинематографии (здесь должно быть название фильма, о котором вы все подумали).
Матрица в математике – это таблица чисел, состоящая из определенного количества строк (m) и столбцов (n).
Вы встречаетесь с ними каждый день, так как любая числовая информация, занесенная в таблицу, уже в какой-то степени считается матрицей.
Примером могут служить:
● список телефонных номеров;
● различные статистические данные;
● табель успеваемости ученика и многое другое.
Сами матрицы всегда обозначаются прописными латинскими буквами (A, B, C…), а элементы матрицы – строчными (a, b, c…). Индексы обозначают местоположение элемента матрицы в системе, причем первое число – это всегда номер строки, а второе – это всегда номер столбца. Например, а23 находится во второй строке и в третьем столбце, а31 в третьей строке и первом столбце и т.д.
Важно произносить элементы матриц правильно, так а23 будет звучать как «а два три», а не «а двадцать три».
Примеры записи матриц
Для чего нужны матрицы
Теперь выясним, для чего нам так нужны матрицы конкретно в математике?
В качестве примера рассмотрим простейшую систему двух линейных уравнений и решим ее методом сложения, который изучают в школьном курсе.
Оказывается, можно решить эту систему уравнений альтернативным способом, используя матрицы, и называется он метод Крамера.
Вы можете подумать, зачем усложнять решение какими-то матрицами?
В данном случае да, при желании можно эту систему и в уме решить. Но представьте себе систему, состоящую хотя бы из 5 линейных уравнений с пятью неизвестными. А если система состоит из 6, 7 или ещё больше уравнений? Решать её школьным методом, мягко говоря, трудоёмко. Зато применяя тот же метод Крамера, решение будет выглядеть достаточно компактно.
Система с тремя уравнениями
В подтверждение вышесказанного рассмотрим систему уравнений с тремя неизвестными и решим её метод Крамера.
Из этого следует, что матрицы – еще один способ решения систем линейных алгебраических уравнений (СЛАУ).
На основе второго примера убеждаемся в том, что матрицы могут применяться в тех случаях, когда применение школьных методов решения СЛАУ не является рациональным.
На самом деле за прошедшие столетия алгебра матриц изучена более, чем достаточно, и тот факт, что матрицы используются повсеместно однозначно подтверждает необходимость их изучения.
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Матрица, ее история и применение
Разделы: Математика
Матрица, её история и применение
Термин « матрица » имеет много значений. Например, в математике матрицей называется система элементов, имеющая вид прямоугольной таблицы, в программировании матрица – это двумерный массив, в электронике – набор проводников, которые можно замкнуть в точках их пересечений. Покерные фишки также имеют непосредственное отношение к матрице. Фишки для покера изготавливаются из высококачественного композиционного материала, зачастую с металлической сердцевиной. В свою очередь композиционный материал или композит имеет матрицу и включенные в нее армирующие элементы (исключение составляют слоистые композиты).
Матрица в фотографии – это интегральная микросхема (аналоговая или цифро-аналоговая), которая состоит из фотодиодов (светочувствительных элементов). Благодаря светочувствительной матрице происходит преобразование спроецированного на нее оптического изображения в электрический сигнал аналогового типа, а при наличии в составе матрицы АЦП, то преобразование происходит в поток цифровых данных.
Матрица – основной элемент цифровых фотоаппаратов, всех современных видео- и телекамер, фотокамер, встроенных в мобильный телефон и системы видеонаблюдения.
Основное значение термин «матрица» имеет в математике.
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. Так же, волшебные квадраты были известны чуть позднее у арабских математиков, примерно тогда появился принцип сложения матриц. После развития теории определителей в конце 17-го века, Габриэль Крамер начал разрабатывать свою теорию в 18-ом столетии и опубликовал «правило Крамера» в 1751 году. Примерно в этом же промежутке времени появился «метод Гаусса». Теория матриц начала своё существование в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу. Термин «матрица» ввел Джеймс Сильвестр в 1850 г.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Матрицы допускают следующие алгебраические операции:
Матрица – множество чисел, образующих прямоугольную таблицу, которая содержит m – строк и n – столбцов. Для обозначения матрицы используется надпись:
А=
аij, где i – номер строки, j – номер столбца
Далее рассмотрим виды матриц.
С=

Матрица, которая содержит только одну строчку или один столбец называется вектором. В таких матрицах можновыделить вектор-строка и вектор-столбец. Так, матрица K – это вектор-строка, а матрица F – вектор-столбец.
K=

Квадратная матрица, у которой в главной диагонали стоят ненулевые элементы, а все остальные – нули называется диагональной матрицей. Матрица L – диагональная матрица третьего порядка. Если ненулевые элементы равны только единицам, то это единичная матрица, она всегда обозначается буквой Е. В нашем случае матрица Е – тоже единичная матрица третьего порядка.
L= 

Если все элементы матрицы нули, то это нулевая матрица. Например, матрица V – нулевая матрица третьего порядка.
V=
Если в данной матрице поменять строки и столбцы местами, то получится транспонированная матрица данной. Например, дана матрица М, каждую строчку этой матрицы перенесем в соответствующий столбец матрицы, стоящей на рисунке рядом. Вторая матрица – это транспонированная матрица матрицы М.
К середине XIX в. матрицы стали самостоятельными объектами математических исследований. К этому времени были сформулированы правила сложения и умножения матриц. Основную роль в их разработке сыграли работы Гамильтона, Кэли и Сильвестра (J.J.Sylvester, 1814–1897). Современное обозначение матрицы предложил Кэли в 1841 году. Исследования Вейерштрасса (K.Th.W.Weierstrass, 1815–1897) и Фробениуса (F.G.L. Frobenius, 1849–1917) далеко продвинули теорию матриц, обогатив ее новым содержанием.
Но существует ещё особая разновидность матриц, называемая магическим квадратом. Магический квадрат – квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Магический квадрат – древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы и эти знаки известны под названием лошу и равносильны магическому квадрату. В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера изображенный на его знаменитой гравюре Меланхолия 1. Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А.де лаЛубера. Рассмотрим этот метод на примере квадрата 5-го порядка. Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата (как в случае числа 1), продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца. Дойдя до правого края квадрата (число 3), продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки (число 5) или угла (число 15), траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
Где ещё применяются матрицы?
В физике и других прикладных науках матрицы – являются средством записи данных и их преобразования. В программировании – в написании программ. Они еще называются массивами. Широко применение и в технике. Например, любая картинка на экране – это двумерная матрица, элементами которой являются цвета точек.
В психологии понимание термина сходно с данным термином в математике, но взамен математических объектов подразумеваются некие «психологические объекты» – например, тесты.
Кроме того, матрицы имеет широкое применение в экономике, биологии, химии и даже в маркетинге.
Также авторы нашли абстрактную модель – теорию бракосочетаний в первобытном обществе, где с помощью матриц были показаны разрешенные варианты браков для представителей и даже потомков того или иного племени, что явилось свидетельством разнопланового применения матриц.
Теперь подробнее остановимся на некоторых областях применения матриц.
Рассмотрим теорию бракосочетаний, о которой уже упоминалось.
В некоторых первобытных обществах существуют строгие правила относительно того, в каких случаях допустимы браки. Эти правила направлены на предотвращение браков между слишком близкими родственниками.
Эти правила допускают точную математическую формулировку в терминах «p-матриц». Одним из первых изложил эти правила в виде аксиом Андре Вейль.
Правила бракосочетания характеризуются следующими аксиомами:
Из аксиом следует, что нужно задать зависимость между типом родителей и типами сыновей и дочерей.
Для установления отношения родства пользовались следующими обозначениями:
Вот примеры видов отношений:
Данные схемы далее объединяются в большие матрицы, где условные обозначения преобразуются в числа. С помощью таких матриц удобно видеть кровное родство в нескольких поколениях.
Понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют чрезвычайно важное значение для экономистов. Объясняется это тем, что значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме.
С помощью матриц удобно записывать некоторые экономические зависимости.
Например, рассмотрим таблицу распределения ресурсов по отдельным отраслям экономики (усл. ед.):
| Ресурсы | Отрасли экономики | |
| Промышленность | Сельское хозяйство | |
| Электроэнергия | 5,3 | 4,1 |
| Трудовые ресурсы | 2,8 | 2,1 |
| Водные ресурсы | 4,8 | 5,1 |
Данная таблица может быть записана в компактной форме в виде матрицы распределения ресурсов по отраслям:
А=
Далее рассмотрим применение матриц в психологии.
Прогрессивные матрицы Равена– тест на наглядное и в то же время абстрактное мышление по аналогии (тест интеллекта), разработанный англ. психологом Дж. Равеном (1938).
Каждая задача состоит из 2 частей: основного рисунка (какого–либо геометрического узора) с пробелом в правом нижнем углу и набора из 6 или 8 фрагментов, находящихся под основным рисунком. Из этих фрагментов требуется выбрать один, который, будучи поставленным на место пробела, точно подходил бы к рисунку в целом. Прогрессивные матрицы Равена разделяются на 5 серий по 12 матриц в каждой. Благодаря увеличению числа элементов матриц и усложнению принципов из взаимоотношений задачи постепенно усложняются как в пределах одной серии, так и при переходе от серии к серии. Имеется также облегченный вариант прогрессивных матриц Равена, предназначенный для исследования детей и взрослых с нарушениями психической деятельности.
На рисунке показаны примеры таких матриц:



Мы рассмотрели основные области применения матриц. Выяснилось, что данный термин употребляется не только в математике, но и в других науках, таких, как информатика, биология, химия, физика, психология, экономика и т. д. Кроме того, матрицы могут быть практически применимы, например, как это делали в первобытном обществе для определения разрешённых вариантов брака.
МАТРИЦА— (нем., Matrize, от лат. matrix матка). 1) в литейном производстве: медная форма для отливки букв, а также монет. 2) в типографском деле: бумажная форма для отливки стереотипа.
С помощью матриц можно решать системы уравнений, в них удобно представлять какие-либо данные.
Таким образом, мы пришли к выводу, что матрицы широко применялись и применяются до сих пор.
Литература:
Что такое матрицы и что с ними делать?
Впервые сталкиваясь с высшей математикой, студенты приходят в ужас. Новые понятия, методики расчетов, схожие между собой, множество действий вводят учащихся в ступор. Если Вы учитесь на факультете, который по минимуму связан с математикой и физикой, то на разбор одной темы в среднем уходит 3-5- пар (притом 1-2 из них лекции, а остальные – семинары и практикумы).
Первым и, пожалуй, одним из простых понятий, встречающихся в математической науке, является матрица. В нашей статье речь пойдет не о знаменитом одноименном фильме, а о математической единице. Сегодня мы расскажем: что это такое и с чем это «есть», как применять на практике.
Что такое матрица?
Впервые с этим понятием сталкиваются студенты 1-2 курсов независимо от факультета и выбранной специальности. В общем виде матрица представляет собой прямоугольную таблицу с числами, притом каждое из них занимает определенное место и положение, имеет собственное обозначение.
Каждая матрица имеет свое имя. Оно обозначается заглавными буквами латинского алфавита: А, В, С и пр.
У каждой матрицы есть свой размер. Одежду подбирать ей не придется, но вот учитывать это параметр при действиях над матрицей нужно обязательно. Размер матрицы определяется, исходя из количества строк и столбцов, которые обозначают m и n соответственно.
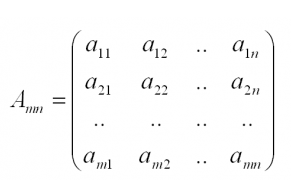
Все числа, образующие таблицу (непосредственно матрицу), называют элементами матрицы. У каждого из них есть свое обозначение с учетом местоположения (строка+столбец). Например, элемент, находящийся в первой строке и первом столбце обозначают а11, а элемент в первой строке и втором столбце – а12.
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Какие действия можно выполнять над матрицами?
Матрицы, как математическая единица, поддаются всем основным действиям: сложение, вычитание, умножение и даже деление. Каждая из операций будет иметь определенный порядок действий и потребует соблюдение конкретных условий.
Особенности сложения и вычитания матриц
Одним из важнейших требований в данном случае является соразмерность матриц. Оно означает, что размер матриц должен быть одинаковым. В противном случае сложить или вычесть один элемент из другого не удастся. При разном количестве элементов произвести необходимые действия не представляется возможным.
Сложение и вычитание соразмерных матриц производится следующим образом: все действия осуществляют над одними и теми же элементами из разных матриц.

Вычитание производится аналогично, поэлементно. Важно отметить, что количество слагаемых (суммируемых или вычитаемых матриц) может быть неограниченно.
Особенности умножения матриц
Умножение необходимо рассматривать в двух вариантах:
Это самый простой вариант развития событий. В данном случае необходимо умножит каждый элемент матрицы на число.
Получить произведение матриц возможно не во всех случаях. Здесь также необходимо соблюдение определенных условий: число столбцов одной матрицы должно быть равнозначным числу строк другой матрицы.
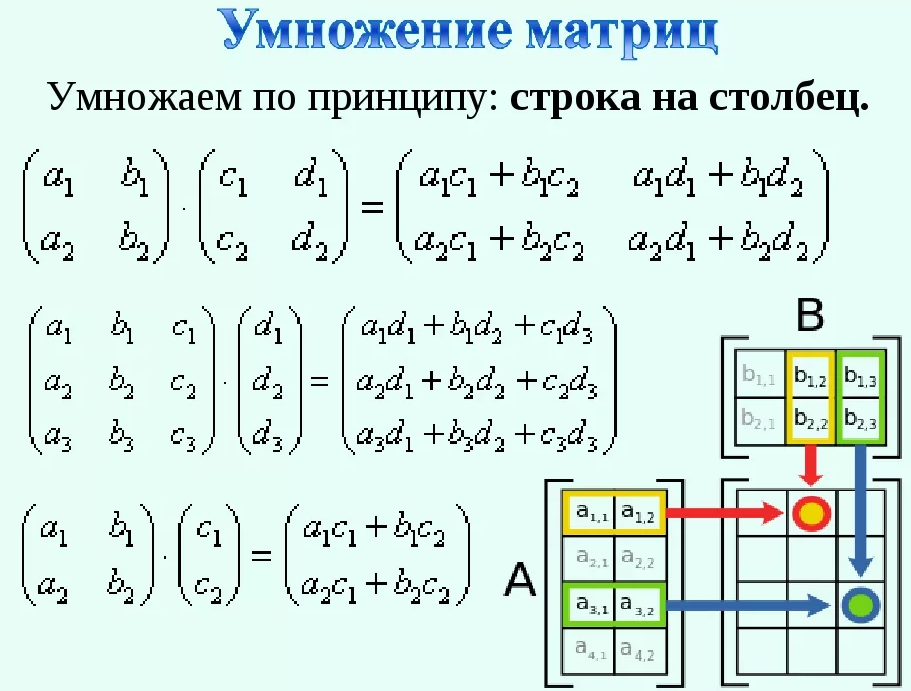
Специфика умножения матриц проявляется в следующем: умножение производится не просто поэлементно, но и с учетом строк и столбцов. Элементы новой матрицы получаются в ходе умножения элементов и суммирования двух произведений. То есть фактически нужно умножать строку на столбец.
Рассмотрим порядок умножения матриц на примере:
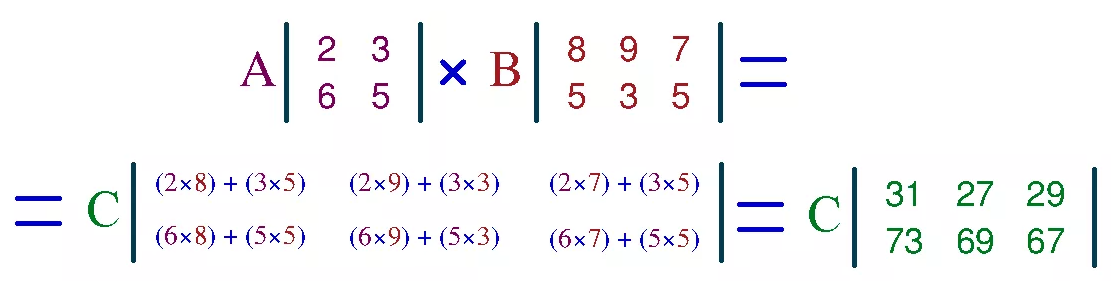
Деление матриц
При делении матриц выделяют новое понятие – обратная матрица, которая обозначается А. Данный критерий действителен только в отношении квадратных матриц (когда число строк равно числу столбцов).

Произведение матрицы А и А даст единичную матрицу Е.
Транспонирование матрицы – это…
У матриц есть одно специфическое действие, когда можно поменять местами строки и столбцы. Такая операция называется транспонированием. Если обычная матрица обозначается А, то транспонированная — А.
Рассмотрим процесс транспонирования на конкретном примере:
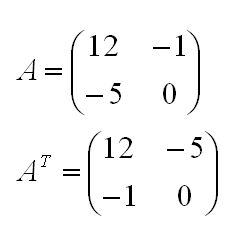
Определитель матрицы – это…
Одним из важнейших элементов матрицы является ее определитель. Данный критерий представляет собой численную характеристику матрицы. Для ее получения нужно, чтобы матрица была квадратной. Расчет определителя производится на основе разности произведений диагоналей: главной и побочной.

Для чего нужны матрицы?
Матрицы успешно используются, как в математике, так и иных науках. В математическом направлении они позволяют просто и быстро решить систему уравнений.
В экономике использование матричных структур целесообразно при решении некоторых задач. При этом важно чтобы вычисление нужного параметра было можно представить в виде таблицы или системы уравнений.
Матрицы также уместны при вычислении в таких науках, как физика, механика, эконометрика и пр. Они упрощают процесс вычисления искомого параметра при грамотной интерпретации известных критериев.
Команда ОЦ DissHelp готова помочь в рении задач и выполнении контрольных, курсовых и дипломных работ для студентов всех направлений обучения с использованием матриц и без них. Наши специалисты грамотно и просто пояснят, как пользоваться ими в науке и жизни, решат любое задание независимо от уровня сложности. Мы гарантируем высокое качество услуг, соблюдение сроков и индивидуальный подход, конфиденциальность данных.
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!

















