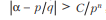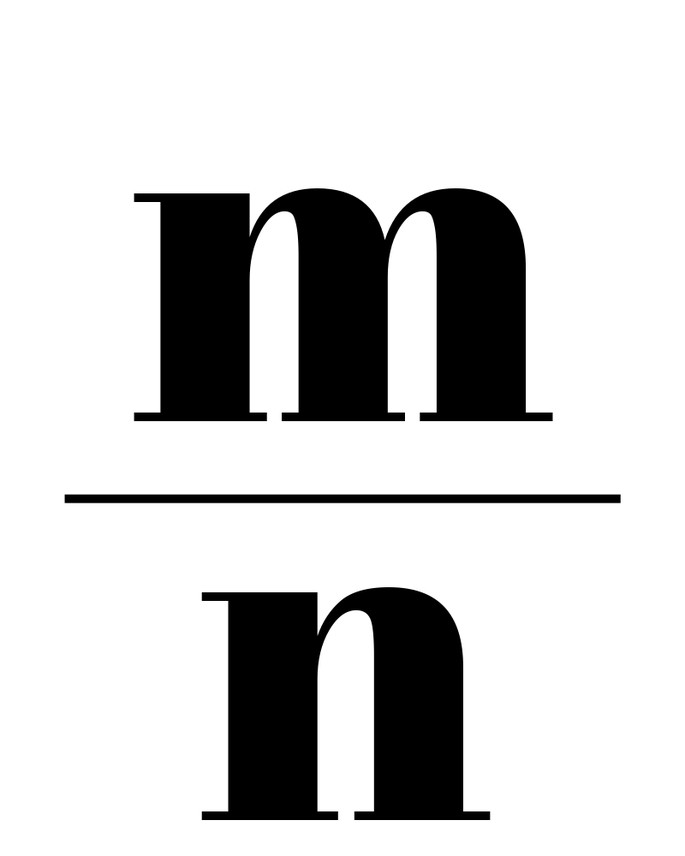Для чего людям понадобились иррациональные числа
Иррациональные числа
Что такое иррациональные числа
Если в ходе решения математической задачи получилась дробь, в которой нельзя полностью разделить числитель на знаменатель, то это иррациональное число.
Существует еще одно условие принадлежности такой дроби к иррациональным величинам. Это отсутствие периодов в наборе цифр после запятой, т.е. нет периодически повторяемой цифровой последовательности.
Иррациональным называется число, которое нельзя представить в виде законченного частного от деления двух целых величин.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С таким множеством сталкивались еще математики древних веков. Для них, например, было понятно, что диагональ квадрата нельзя разделить на длину его стороны и получить при этом не бесконечную дробь. Аналогичным образом характеризуется соотношение постоянной π выбранной окружности к диаметру.
Говоря простыми словами, если в обычной десятичной дроби после запятой обнаруживается бесконечное количество цифр и в них отсутствует повторяемость периодов, то это представитель иррационального множества.
Термин, обозначающий данную категорию цифр, произошел в результате сложение двух частей: ratio, что означает «соотношение» и ir, что означает отрицание. В итоге слово «иррациональный» закрепилось за дробями, не способными дать четкое соотношение.
Например, диагональ квадрата, сторона которого равна 1, не может быть представлена рациональным числом, но она имеет определенное числовое выражение. К таким же случаям можно отнести √5, √7, √10. Именно для выражения таких значений введено множество иррациональных чисел, каждое из которых может быть представлено бесконечной непериодической дробью (в отличие от рационального, которое можно представить периодической десятичной дробью).
Виды, место в общей классификации, как обозначаются
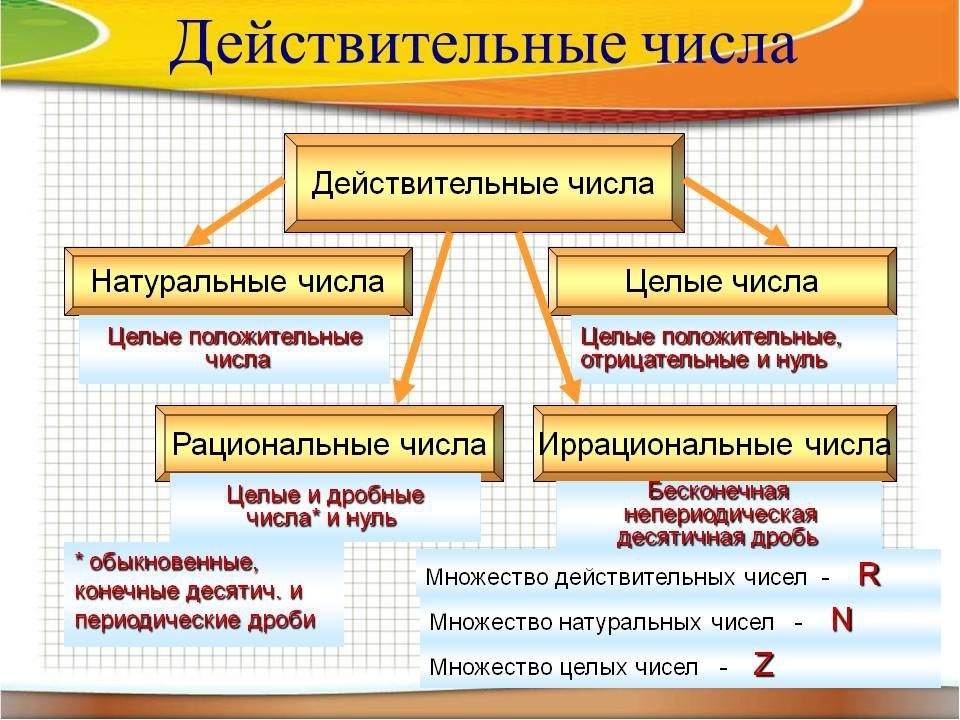
В арифметической классификации иррациональным числам выделено четкое место, наравне с рациональными, которые делятся на целые и дробные.
Для обозначения множества используют букву I. Его математическое выражение выглядит так: I=R-Q.
Алгебраические и трансцендентные
В алгебре те величины, которые могут являться квадратными корнями с целыми коэффициентами из многочленов, относятся ко множеству алгебраических. Те же, которые не могут выступать в этой роли, образуют другое множество — трансцендентных.
Происхождение термина «трансцендентный» объясняется его переводом с латыни: transcendentis — выходящий за границы. Таким образом, это величины, которые находятся за пределами множества чисел, которые могут стать квадратным корнем с целым коэффициентом из различных многочленов.
О необходимости введения такого множества впервые заговорил в 1775 году Леонард Эйлер. Стоит отметить, что во время его деятельности еще не было известно никаких трансцендентных значений.
Вычислить их пример не удавалось математикам и в последующие много лет. Лишь в 1844 году Ж.Луивилль привел всем их пример. Его теореме досталось лидирующее место в теории диофантовых приближений.
Алгебраические числа плохо приближаются рациональными, в частности, если алгебраическое число αn (n — наименьшая степень многочлена P(x) с целыми коэффициентами такого, что P(α)=0), то для любой дроби p/q справедливо выражение:
Где С — константа, зависящая от α.
Все числа типа m/n, где n отлично от нуля, а m и n представлены целыми значениями, являются алгебраическими. Для них справедливо равенство: nx-m=0.
К понятию «алгебраические», кроме рациональных, отнесены иррациональные, для которых характерна формула n √m. При этом m и n представлены целыми числами, а n больше либо равно 2.
При любых действиях с алгебраическими числами (сложение, вычитание, деление либо умножение) результат решения будет алгебраической величиной. Кроме этого, алгебраическими будут корни многочленов, коэффициенты которых также отнесены к этому множеству.
Для чего они используются
В математике использование иррациональных чисел объясняется списком их свойств. Например, возможность точного определения величины, полученной в результате извлечения квадратного корня из 2-х, не всегда нужна. Так, в геометрии измерения длины гипотенузы часто производят приблизительно (1,4, 1,41 и т.д.). Извлечение точного квадратного корня из 2-х понадобится только при работе с абстрактной математической моделью.
Однако такие ситуации в науке существуют. Поэтому существование множества иррациональных чисел оправданно. С помощью них можно высчитать дедекиндово сечение в рациональных числах, у которых отсутствует самое большое в нижнем сегменте и самое малое — в верхнем.
Представители иррациональных значений позволяют уплотнить числовую прямую с нанесенными рациональными значениями, таким образом, что между каждой такой парой можно записать иррациональное.
Бывают случаи, что, складывая два иррациональных значения, получают рациональное.
Например, в результате сложения корня из семи (любой степени) и такого корня из семи, только со знаком минус, получается рациональное число — 0.
Сумма двух положительных иррациональных чисел также может быть рациональным значением. Однако при сложении рационального и иррационального в итоге всегда получается представитель иррациональных. Такое свойство называется отсутствием у множества замкнутости.
Исходя из сказанного, следует сделать вывод, что введение множества иррациональных чисел необходимо для увеличения точности. Например, когда между натуральными числами единицей и двойкой не было промежуточных величин, нужно было ее ввести для расширения диапазона точности.
Как вычислить иррациональное число, действия
Чтобы вычислить иррациональное число проще всего предположить, что оно рациональное и его реально представить в виде дроби p/q, не поддающейся сокращению. В результате преобразующих действий доказывается, что натуральные p и q не являются взаимно простыми. Тогда понятно, что это именно иррациональное значение, а предположение о рациональности взятой дроби ошибочно.
В целом же под понятием «иррациональное» понимается число, записать которое в виде десятичной дроби невозможно. Часть после запятой будет бесконечной:
«золотого сечения» 1,61803398…
При этом степень точности результата зависит от количества знаков, взятых после запятой.
Правда, при описании таких величин чаще используют логарифмы, корни, степени и т.п.
Чтобы в текущий момент определить принадлежность данного числа к категории иррациональных, можно воспользоваться онлайн калькулятором, в котором можно произвести вычисления до оговоренной точности.
Задание: рассчитать рациональность заданных значений.
На калькуляторе нужно задать число в виде правильной дроби (по определению, оно рациональное). Исходя из этого, результативным будет определение иррационального компонента для выражений в виде корней (со степенью n).
Видим, что, имея дело с квадратными и кубическими корнями, извлекаемая величина может быть рациональной.
Буддийский физмат: как гёделевская неполнота и иррациональные числа породили нашу Вселенную
Каждый человек в определенный момент своей жизни начинает задаваться вопросами: «Почему существует Вселенная?», «Что такое время?», «Что было до Большого Взрыва?».
Со мной это произошло несколько лет тому назад. Я стал искать ответы на эти вопросы, пытаясь найти их везде: в научно-популярных книгах по физике, в древнегреческой и древнеиндийской философии, в популярных и эзотерических религиях. В каждом из этих направлений человеческой мысли я не находил окончательной истины, но находил одну из её бесконечных граней.
Наш ум анализирует поток сырых сенсорных данных от органов чувств: он различает разные цвета, звуки, запахи и конструирует из них цельную картину сознания. Именно из-за этих базовых свойств нашего ума: различения базовых частиц восприятия и конструирования из них абстракций, мы видим внешний мир как набор отношений между абстрактными объектами.
Пустота материи, пространства и времени
Если мы рассмотрим любые предметы, которые мы считаем материальными, с точки зрения буддийской доктрины пустоты, то они окажутся иллюзией и «исчезнут». Виктор Пелевин в своём известном романе «Чапаев и Пустота» рассказывал метафорическую историю про Будду, указывавшего на разные предметы своим мизинцем, после чего эти предметы тотчас исчезали.
Наука о пустоте
Вот её определение из Википедии:
Если однажды мы встретимся с представителями внеземных цивилизаций, то можно с уверенностью сказать, что и в их математическом аппарате дважды два будет равно четырем. Конечно, они будут обозначать цифры и операции другими символами, но суть будет та же самая. С помощью математических выражений мы сможем найти и другие сходства с инопланетной наукой: у них ведь будут те же самые, что и у нас, законы физики, химии и частично даже биологии.
Но что, если мы встретимся с существами из вообще другой Вселенной с отличными от наших законами физики? Какие точки соприкосновения с ними мы сможем найти? Очевидно, что единственной общей вещью между нами и иновселянами будет математика. Ведь даже несмотря на отличные от наших законов физики, законы математики в их Вселенной будут такими же как и у нас. Невозможно существование какой-то иной математики. Математика никак не зависит от времени, пространства и любых других свойств той Вселенной, в которой мы существуем. Ведь если подумать, то даже до Большого Взрыва утверждение «дважды два равно четыре» должно было быть верным.
Рассуждая схожим образом, древнегреческий философ Платон пришел к выводу, что математика обладает независимым бытием и существует в неком нематериальном «мире форм». В доказательство своему утверждению Платон приводил правильные многогранники, позже в его честь названные платоновыми телами.

Рождение Вселенной
Мы подошли к самой красивой части «буддийского физмата»: гипотезе рождения Вселенной. Эта часть содержит достаточно много непростой метафизики, но начинается она с единственного постулата: все вещи существуют симметрично относительно друг друга. Я употребляю слово «существует», а не «возникает», потому что возникновение предполагает некий процесс во времени, а в мире абсолютных форм нет времени, оно появляется позже.
Одной из таких структур становятся иррациональные и трансцендентные числа, то есть числа не представимые в виде целочисленной дроби или корня уравнения. Количество цифр после запятой у таких чисел бесконечно. Самым известным трансцендентным числом является число π:
3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989.
Нетривиальные нули дзета-функции Римана (их мнимые части) соответствуют собственным значениям некоторого эрмитового оператора (неограниченного самосопряжённого оператора в гильбертовом пространстве).
Оказалось, что квантовый хаос прекрасно описывается распределением нетривиальных нолей функции Римана:

Британский научно-популярный писатель Джон Дербишир задавался вопросом на этот счёт:
Нетривиальные нули дзета-функции Римана появились при исследовании распределения простых чисел. Собственные значения случайных эрмитовых матриц появились при исследовании поведения систем субатомных частиц, подчиняющихся законам квантовой механики. Скажите, пожалуйста, что вообще может быть общего между простыми числами и поведением субатомных частиц?
Если бы он был знаком с «буддийским физматом», он бы знал ответ! Более того, «буддийский физмат» проливает свет и на то, почему наш мир на микроуровне, изучаемом квантовой механикой, кажется случайным, а на макроуровне абсолютно стабилен. Каждое следующее простое число случайно и невычислимо по точной формуле, но их распределение строго подчинено дзета-функции Римана. А каждая следующая цифра после запятой в иррациональном числе тоже абсолютно случайна: , но их общее количество на большом масштабе абсолютно стабильно: например, в первом миллионе цифр после запятой числа Пи 99959 нулей, 99758 единиц, 100026 двоек, 100229 троек, 100230 четвёрок, 100359 пятёрок, 99548 шестёрок, 99800 семёрок, 99985 восьмёрок и 100106 девяток. Получается, простые и иррациональные числа, прямо как наша Вселенная, строго детерминированы математикой, но кажутся случайными на микромасштабах.
Вывод
Иррациональные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Рациональные числа — это те, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами
Иррациональные числа — определение, свойства и примеры
История открытия
Одни учёные считают, что иррациональные числа были открыты Пифагором. Другие полагают, что существование таких величин было выявлено пифагорейцами в V веке до нашей эры. Третьи выдвигают версию, что открытие принадлежит древним учёным Азии.

Несмотря на то что возникновение нового типа чисел связывают с именем Пифагора, сам великий учёный этих величин не признавал. Математик основывал свои труды на рациональности значений, а потому их иные виды были неприменимы к его теориям. Из-за огромного авторитета учёного иррациональные значения стали использоваться в науке только после его смерти.
Аристотель доказал иррациональность квадратного корня из 2. Теодор из Кирены привёл подобные доказательства в отношении корня из 3, 5 и так далее. Есть версия, что даже термины для соответствующей теории ввёл этот математик. Его ученик Теэтет на основании указанных данных создал общее учение об иррациональности. Полная теория иррациональных количественных значений Эвклид изложил в пятой книге «Начал».
Понятие и характеристика
Огромным прорывом в математической науке стали числа, которые называются иррациональными. Какие-либо ограничения, связанные с целыми величинами или обыкновенными дробями, были сняты. Люди получили возможность открывать и даже изобретать новые количественные значения.
Иррациональным считается вещественное число, не являющееся рациональным. Оно не может быть представлено в виде арифметической дроби n/m, где числитель и знаменатель являются целыми величинами, а n не равно 0. Также подобные значения невозможно точно выразить целой величиной. Это значит, что иррациональные числа всегда выглядят, как бесконечные непериодические десятичные дроби. Для их обозначения применяют радикалы или специальные буквы, например, е, π. Множество чисел обозначается заглавной буквой в полужирном начертании без заливки.
В геометрии оно представляется в качестве отрезка, длина которого несоизмерима с единичной. Об этой несоизмеримости упоминали и древние математики. Они установили, что диагональ квадрата не имеет общей меры с его стороной, что равносильно иррациональности корня из 2.

Не всякая величина из множества значений, не относящихся к рациональным, так известна, как число π. В школьной программе его часто определяют, как 3,14, но истинный показатель π значительно ближе к 3. Следует отметить, что даже известная длинная десятичная дробь является лишь приближённым вариантом, поскольку указанное число нельзя точно установить. Дробь, которую используют для этого, бесконечна, а цифры в ней распределяются без какой-либо закономерности.
Самыми известными примерами таких иррациональных чисел являются:
Математиками составлены специальные таблицы величин, не являющихся рациональными. Но так как множество бесконечно, определить тип значения по данным таблицам довольно сложно.

Зачастую понять, что число иррационально, можно по его соответствию одному из перечисленных признаков:
Но в ряде случаев установить иррациональность значения возможно только посредством доказательства. К примеру, школьникам часто дают задание доказать, что число log3 4 не относится к рациональным.
Отличительные качества
Значения, которые нельзя выразить дробью, существенно отличаются от других чисел. К их уникальным свойствам относятся следующие:

Виды преобразования выражений
Иррациональные выражения содержат операцию извлечения корня. Это особые записи, состоящие из радикалов и знаков алгебраических действий.
Во время преобразования таких выражений нельзя допускать сужения области допустимых значений. С ними разрешается проводить любые из основных тождественных преобразований:
В основе подобного упрощения выражений лежат действия, общие для всех количественных значений. Поэтому в процессе преобразования этих записей необходимо сохранять установленный порядок выполнения действий.
Замена исходной записи
Подкоренное выражение можно заменить тождественно равным, то есть математической записью, значение которой будет равно исходному. Следует учитывать, что равенство должно соблюдаться при любых допустимых значениях переменных, которые входят в состав обоих выражений.
Это утверждение основывается на единственности корня из числа. Иными словами, нет значения, которое, отличаясь от исходной величины, сохраняло бы равенство с нею.
Использование свойств корней
Для упрощения сложных выражений часто применяются свойства корней, к примеру, перемножение их степеней. Делать это необходимо в соответствии со специальными формулами.

Особое внимание при работе следует обращать на отрицательные числа и выражения с переменными. В ряде случаев для применения формул такие значения сначала придётся привести к тождественно равным, которые подойдут для дальнейшего использования свойств корней.
Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом. После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.
Обратным изменением является вынесение множителя из-под радикала. Его используют в случаях, когда степень корня равна степени множителя под радикалом. В таких ситуациях указанный множитель можно извлечь и тем самым упростить выражение.
Изменение дробей
Иррациональные математические записи могут содержать дроби с радикалами в делимом или делителе. С ними разрешается проводить любые действия, относящиеся к основным преобразованиям дробных чисел:

Избавление от иррациональности в знаменателе
Освобождение от иррациональности в знаменателе представляет собой преобразование дроби путём её замены на тождественно равную с делителем, не содержащим корней и степеней. Для этого необходимо последовательно провести два действия:
Переход к степеням
Переход от радикалов к степеням осуществляется на основе равенства, давшего определение степени, которая имеет рациональный показатель. При этом используется следующая формула:

Если же величина под радикалом отрицательная или там находится выражение с переменными, то перед использованием формулы подкоренное значение необходимо преобразовать. Для этого следует применять свойства степеней.
Математические действия
Иррациональные выражения записывают друг за другом с сохранением знаков и лишь после этого складывают или вычитают. Иногда их преобразуют в подобные, то есть имеющие одинаковые подкоренные значения, а затем проводят арифметические действия.
Чтобы найти произведение выражений с одинаковыми радикалами, умножают значения, находящиеся под знаком корня. Полученный результат вносится под корень изначальных выражений.
При делении степени корней делимого и делителя также должны быть равны. Если это условие соблюдено, то первое выражение делится на второе, после чего итог действия записывается под исходный знак радикала.

Правила сравнения
Иногда для решения математических задач необходимо провести сравнение иррациональных значений. При этом необходимо руководствоваться следующими правилами:
Для возведения иррациональной величины в степень необходимо возвести в неё значение под радикалом. Если величина корня равна степени, то в итоге число или выражение выносится из-под корня неизменным, поскольку возникают взаимно сокращающиеся действия.
Если иррациональное выражение находится под корнем, то для его извлечения показатели радикалов умножают. Этот метод позволяет упрощать извлечение корней четвёртой, шестой, восьмой, девятой степени.
Иррациональные числа можно узнать по специальным буквам, используемым для их обозначения, или по написанию в виде десятичных дробей, не имеющих окончания. Выражения этого типа легко отличить по наличию радикала. С подобными значениями проводят те же действия, что и с другими вещественными числами. Их можно умножить, сложить, сравнить и так далее.