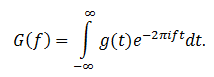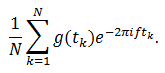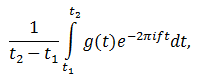Для чего нужен ряд фурье
Простыми словами о преобразовании Фурье
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.

Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).
Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.
Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.
Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:
Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T
Преобразование Фурье: самый подробный разбор
Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.
Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.
Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.
Здесь и пригодится знание преобразования Фурье.
Что такое звук в математическом смысле?
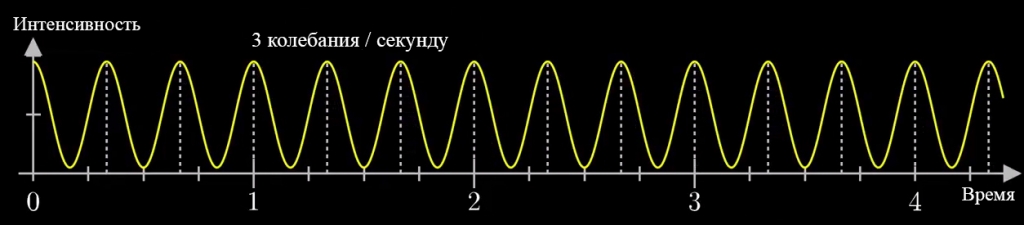
Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.
Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.
Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.
Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.
Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?
Геометрическая интерпретация преобразования Фурье
Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.
В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.
1. Наматываем сигнал
Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.
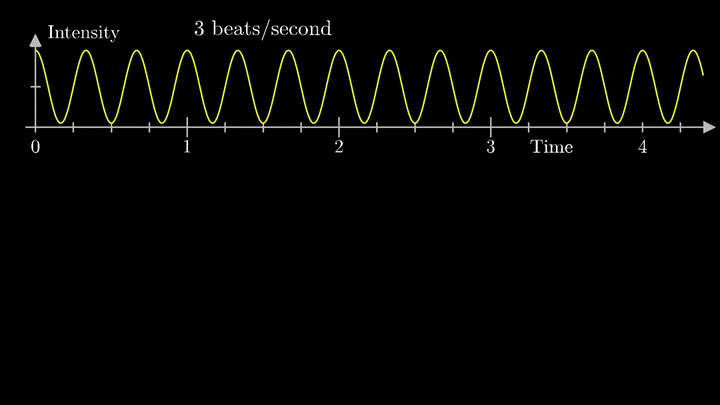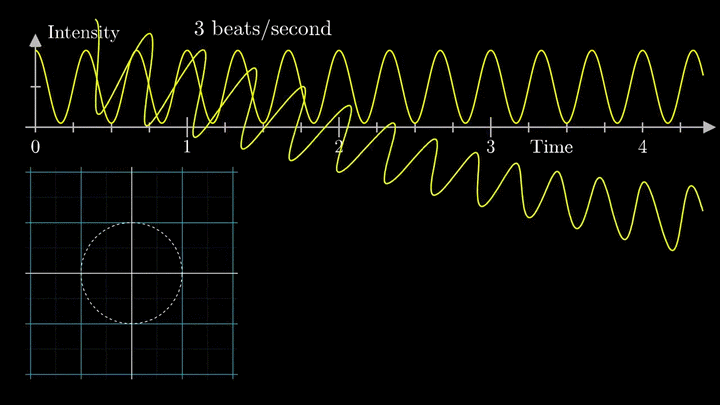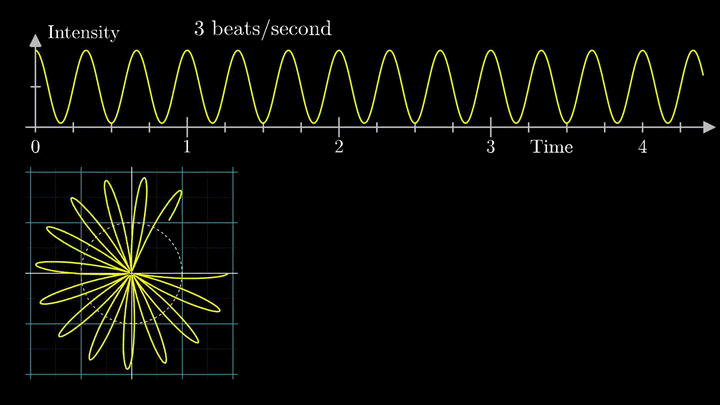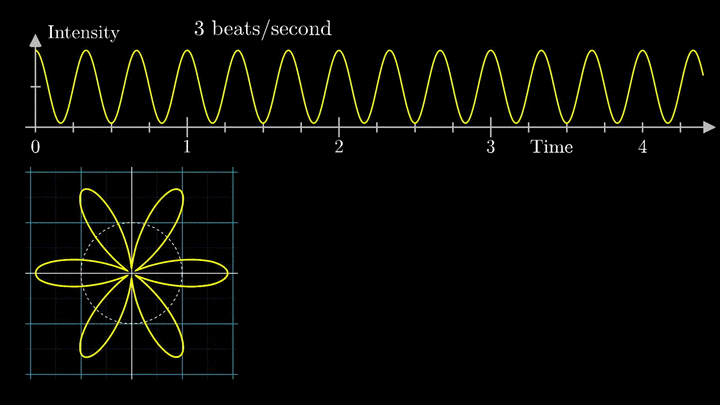
Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения fВ = 0.5 об/с.
Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная «намотка» сливается с началом координат, а при приближении к максимумам – отклоняется.
Пока выглядит не особо информативно, не так ли?
А теперь увеличим частоты намотки.
Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения fВ = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.
2. Ищем центр масс
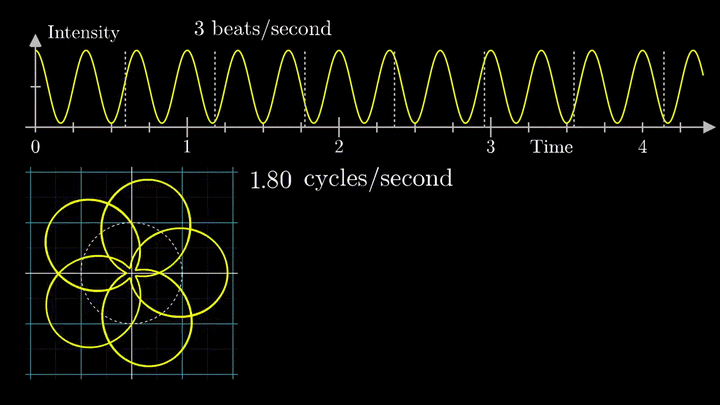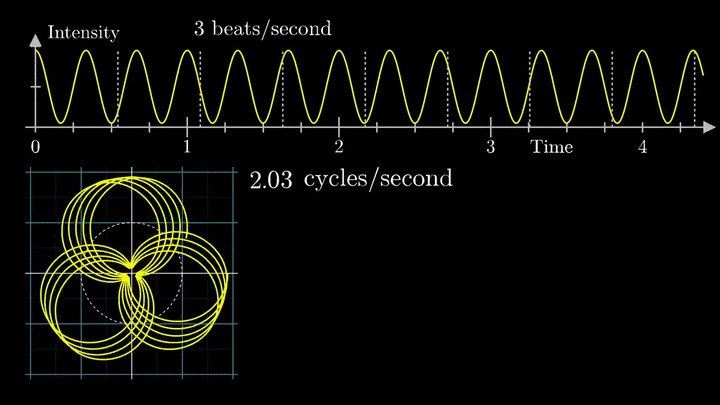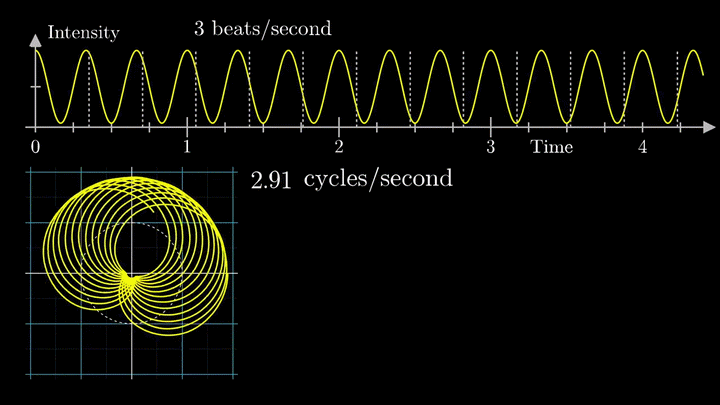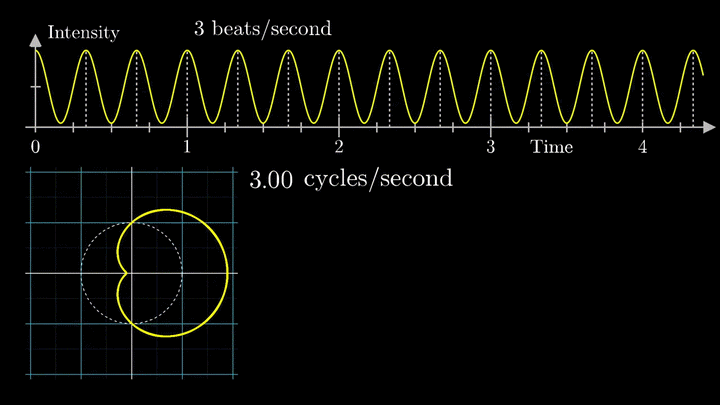
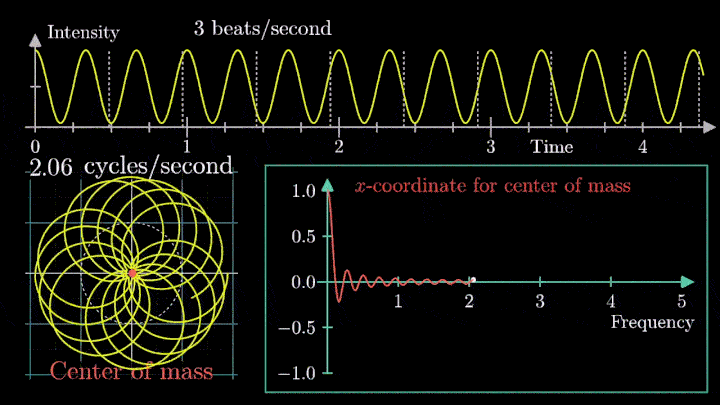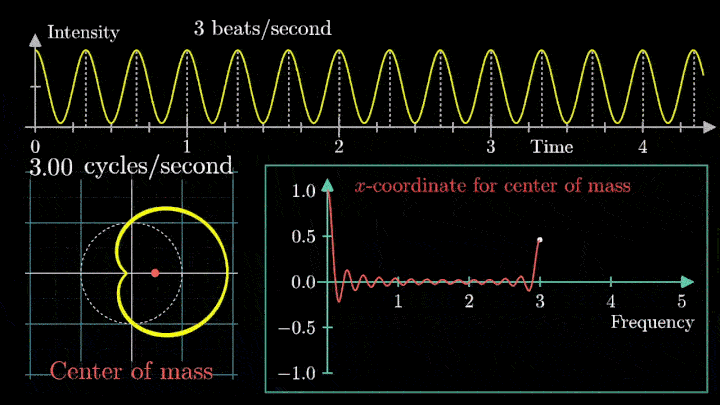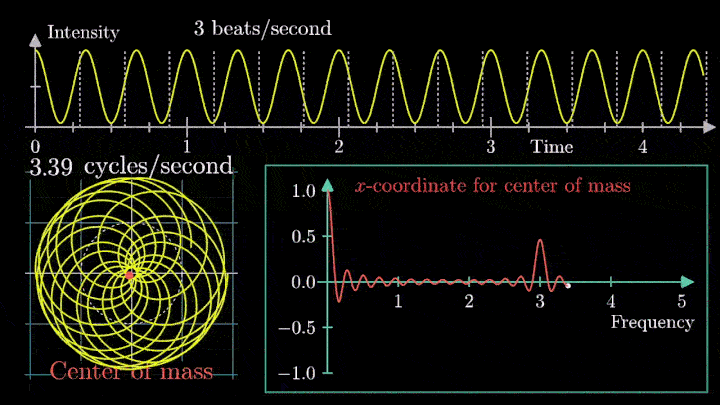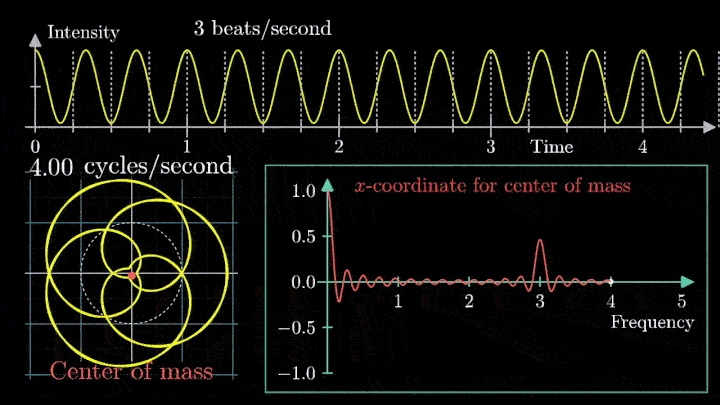
Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).
Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.
Тогда что означает всплеск на низких частотах?
3. Анализируем влияние смещения
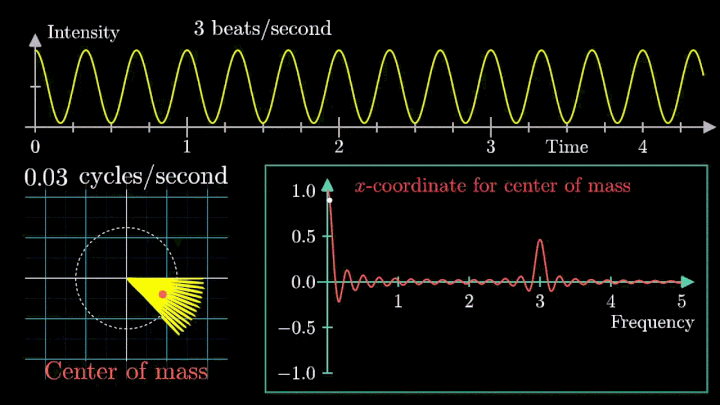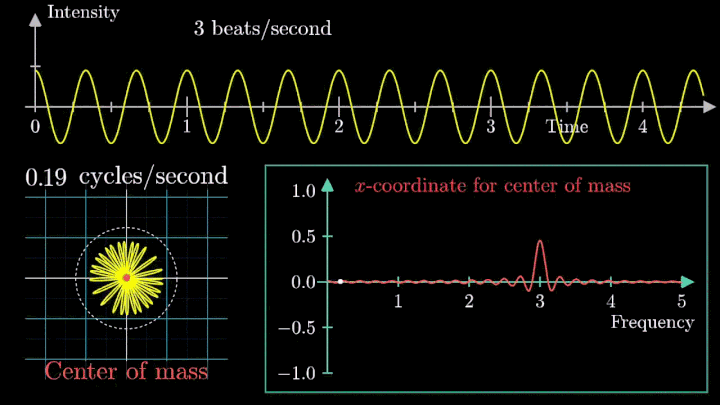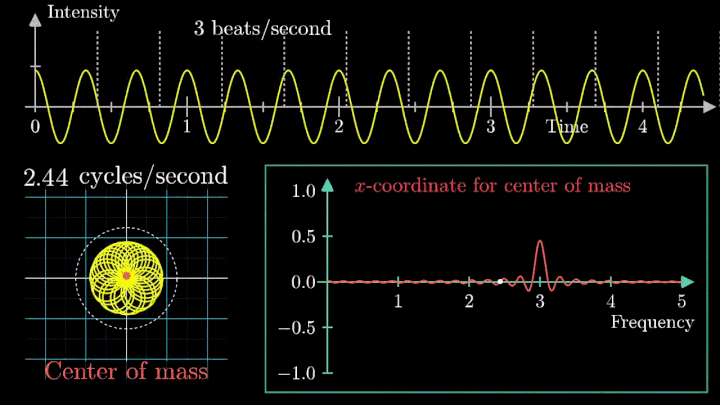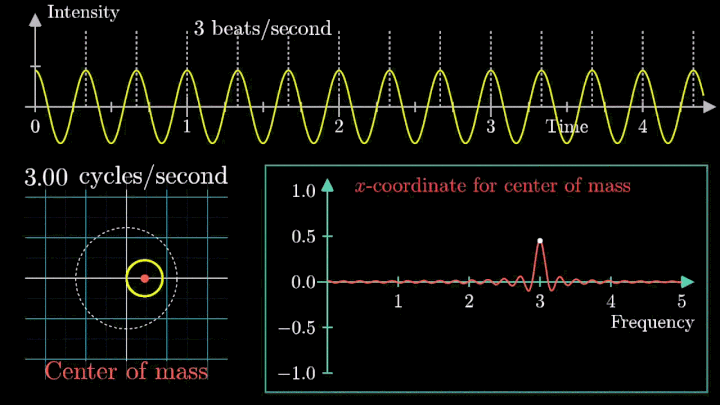
Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.
При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.
Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.
Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.
Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.
Таким образом, на графике остался только один резкий скачок.
Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.
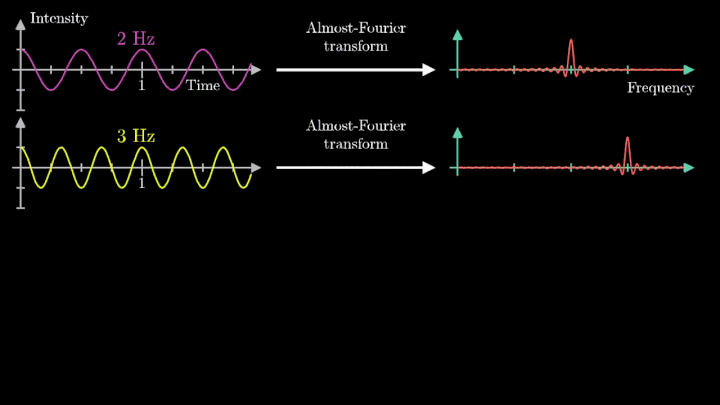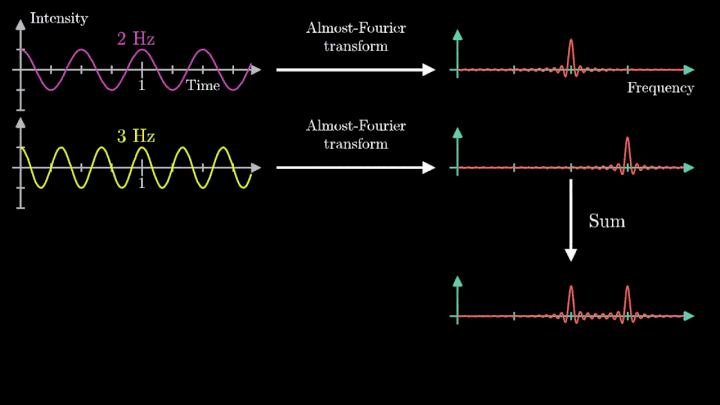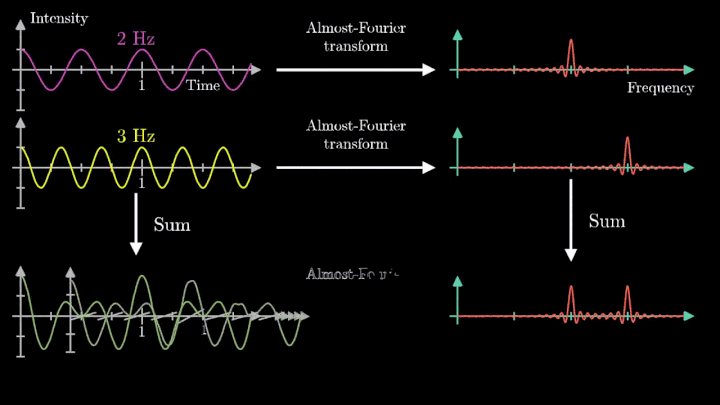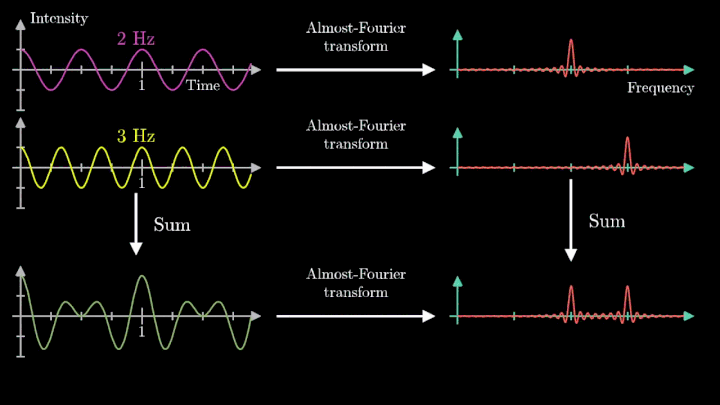
4. Выделяем частоты полигармонического сигнала
Мы наблюдаем два пика в точках fВ = 2 об/с и fВ = 3 об/с, что соответствует частотному составу исходной суммы.
Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.
Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.
Вывод преобразования Фурье
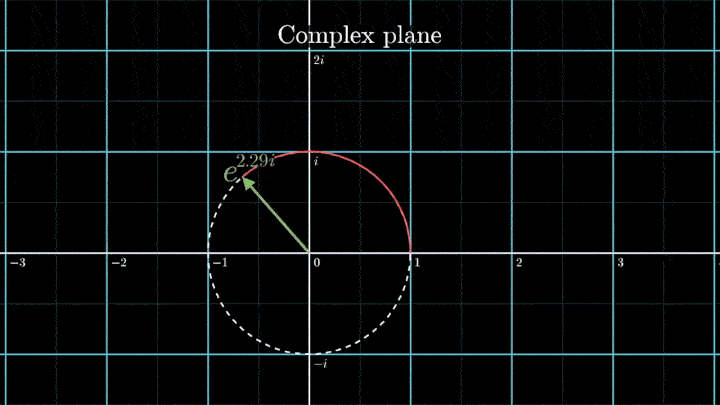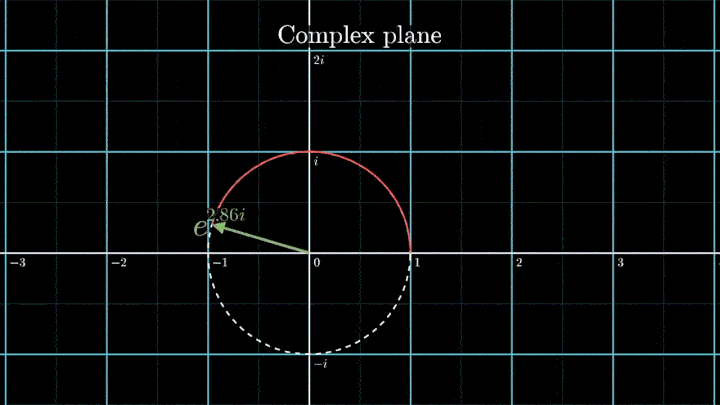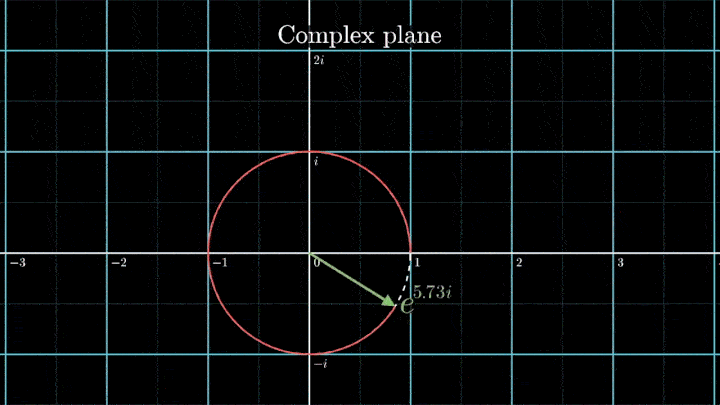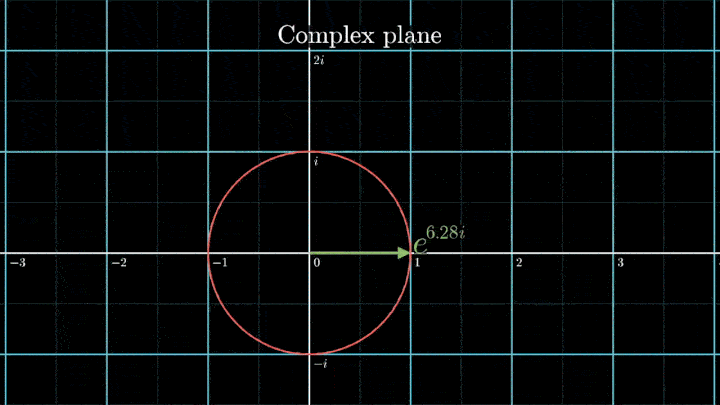
В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:
Геометрически это соотношение означает, что при любом φ точка e iφ на комплексной плоскости лежит на единичной окружности.
Построим радиус-вектор e iφ при разных значениях φ.
При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.
Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:
Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:
где t1 и t2 – границы интервала, на котором рассматривается сигнал.
Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.
Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.
Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.
Применение преобразования Фурье для фильтрации
Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.
При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.
После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.
Курсовая «Ряды Фурье и их применение»
Министерство образования и науки Российской Федерации
федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Оренбургский государственный педагогический университет »
Кафедра математического анализа и методики преподавания математики
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
РЯДЫ ФУРЬЕ И ИХ ПРИМЕНЕНИЕ
Направление подготовки: 050.100.62 педагогическое образование
Профиль подготовки: математика
Форма обучения: очная
Ишматова Айгерим Кайрбековна,
3 курс, 304-М группа
Оглавление
Введение
Разложение функций в ряд Фурье – это математический прием, который можно наблюдать и в природе, если использовать прибор, чувствующий синусоидальные функции.
Данный процесс происходит, когда человек слышит какой-либо звук. Ухо человека устроено таким образом, что может чувствовать отдельные синусоидальные колебания давления воздуха разной частоты, что, в свою очередь, позволяет человеку распознавать речь, слушать музыку.
Ухо человека воспринимает звук не целиком, а через составляющие его ряда Фурье. Струны музыкального инструмента производит звуки, представляющие собой синусоидальные колебания различных частот. Действительность разложения света в ряд Фурье представляет радуга. Зрение человека воспринимает свет через некоторые его составляющие разных частот электромагнитных колебаний.
Преобразованием Фурье является функция, которая описывает фазу и амплитуду синусоид, определенной частоты. Это преобразование используют для решения уравнений, описывающих динамические процессы, которые возникают под действием энергии. Ряды Фурье решают задачу выделения постоянных составляющих в сложных колебательных сигналах, что позволило правильно трактовать полученные данные экспериментов, наблюдений в медицине, химии и астрономии [8].
Открытие данного преобразования принадлежит французскому математику Жан Батисту Жозефу Фурье. В честь, которого впоследствии было и названо рядом Фурье. Первоначально ученый нашел применение своего метода при изучении и объяснении механизмов теплопроводности. Было предположено, что изначальное нерегулярное распределение тепла можно представить в виде простейших синусоид. Для каждой, из которых будет определен температурный минимум, максимум и фаза. Функция, описывающая верхние и нижние пики кривой, фазу каждой гармоники называется преобразованием Фурье от выражения распределения температуры. Автор преобразования предложил способ разложения сложной функции в виде суммы периодических функций косинуса, синуса [2].
Целью курсовой работы является изучение ряда Фурье и актуальности практического применения данного преобразования.
Для достижения поставленной цели были сформулированы следующие задачи:
1) дать понятие тригонометрического ряда Фурье;
2) определить условия разложимости функции в ряд Фурье;
3) рассмотреть разложение в ряд Фурье четных и нечетных функций;
4) рассмотреть разложение в ряд Фурье непериодической функции;
5) раскрыть практическое применение ряда Фурье.
Объект исследования: разложение функций в ряд Фурье.
Предмет исследования: ряды Фурье.
Методы исследования: анализ, синтез, сравнение, аксиоматический метод.
1. Ряды Фурье в действительной области
1.1. Понятие периодической функции
В природе и технике мы часто сталкиваемся с периодическими функциями времени. Процессы, связанные с работой любой машины, любого механизма, процессы и явления, изучаемые в курсе физики, электротехнике дают нам примеры такого рода величин. В настоящее время периодические функции хорошо изучены и широко используются в различных областях техники.
Определение. Число называется периодом функции если для любого из области определения функции числа также принадлежат области определения и
Поэтому, обычно говоря о периоде функции, имеют ввиду наименьшее положительное число, удовлетворяющее равенству (1).
то функции и – периодические функции с периодом 2 Аналогично, в силу равенств
Отметим некоторые свойства периодических функций.
1) Сумма, разность, произведение и частное периодических функций периода Т является периодической функцией того же периода Т.
Так, например, функция – периодическая функция периода
2) Если функция имеет период Т, то функция имеет период .
Действительно, для любого
Например, для функции имеем:
Следовательно, эта функция имеет период и, по предыдущему свойству, такой же период будет иметь функция
Преобразуем последний интеграл:
В частности, если и из (3) следует
1.2. Тригонометрический полином
Это периодическая функция с периодом Имеем:
График синусоидальной функции получается из графика синусоиды следующим образом:
1) растяжением по оси с коэффициентом растяжения ;
2) сжатием графика с коэффициентом сжатия ;
2) Растянем этот график по оси в 2 раза и получим график функции
, изображенный на рисунке 2.
4) Сместим полученный график влево на и получим искомый график, изображенный на рисунке 4.
Сложение гармоник одной частоты (одного периода) дает гармонику той
же частоты. Действительно,
дает более сложную периодическую функцию, чем синусоидальная функция.
Определение. Функция вида
называется тригонометрическим полиномом n -го порядка.
Прибавим к сумме (7) постоянное слагаемое означающее сдвиг начала отсчета. Получим
Но оказалось, что если брать конечное число гармоник, то не всегда удается представить в виде суммы (8). В общем случае такое представление возможно, только если число слагаемых бесконечно, т.е.
Отметим несколько фактов, касающихся сходимости ряда (9).
В дальнейшем будем решать задачу разложения сложного колебания на сумму простых гармоник.
Определение. Представление периодических функций в виде суммы гармоник, называется гармоническим анализом.
1.3. Ортогональность тригонометрической системы функций
Определение . Нормой функции на отрезке называется число
Пример. Рассмотрим систему тригонометрических функций 1,
Ортонормированный система (1.10) не будет, так как
Учитывая последние равенства, получаем, что ортонормированной будет система функций
Заметим, что функции системы (10) ( а также системы (11)) линейно независимы.
Аналогично можно показать, что на система функций
является ортогональной, а система функций
Ортогональную (ортонормированную) систему функций можно считать аналогом ортогонального (ортонормированного) базиса в конечномерном евклидовом пространстве. Как мы позднее убедимся, имеется класс функций, которые являются линейными комбинациями функций ортогональной (ортонормированной) системы, причем слагаемых в линейной комбинации может быть бесконечное число. Линейная комбинация с бесконечным числом слагаемых представляет собой ряд. Использование ряда как функции связано с вопросами сходимости этого ряда.
Рассмотрим разложение функции по тригонометрической системе функций (10).
1.4. Тригонометрический ряд Фурье
Определение. Тригонометрическим рядом Фурье функции на отрезке называется разложение этой функции по тригонометрической системе функций (10), т.е. ряд
Определение. Числа — называются коэффициентами тригонометрического ряда Фурье [2] .
1) Интегрируя почленно ряд (14) будем иметь:
(равенство нулю интегралов показано ранее, при доказательстве ортогональности системы (10)). Отсюда находим
3) Аналогично, умножая ряд (14) на и почленно интегрируя, получим:
Таким образом, получили:
Найти ряд Фурье для функции – значит найти коэффициенты по формулам (15) и записать тригонометрический ряд (14) с этими коэффициентами [2].
1.4.1. Условия разложимости функции в тригонометрический ряд Фурье
Если непрерывная (или кусочно-непрерывная) функция на монотонна или кусочно-монотонна, то в любой внутренней точке она имеет левый и правый предел, т.е. существуют
Теорема (Дирихле) . Пусть функция определена на и удовлетворяет на этом отрезке условиям:
непрерывна или имеет конечное число точек разрыва первого рода (т.е. кусочно-непрерывна);
монотонна или имеет конечное число точек экстремумов (т.е. кусочно-монотонна).
. То есть на границах отрезка функция равна среднему арифметическому левого предела функции в точке и правого предела функции в точке [9].
Условия 1) и 2) теоремы Дирихле называются условиями Дирихле.
1) определены для всех и, следовательно, тригонометрический ряд Фурье определен для всех ;
2) сумма тригонометрического ряда (14) является функцией периодической с периодом ;
3) во всех точках непрерывности функции на отрезке и, следовательно, и в остальных точках непрерывности функции (т.к. обе функции периодические с периодом ).
1.5. Ряд Фурье для четных и нечетных функций
Рассмотрим симметричный интеграл
Следовательно, если четная функция, то (т.е. график четной функции симметричен относительно оси и
Т.е. симметричный интеграл от четной функции равен удвоенному интегралу по половинному промежутку интегрирования, а симметричный интеграл от нечетной функции равен нулю.
Отметим следующие два свойства четных и нечетных функций:
1) произведение четной функции на нечетную есть функция нечетная;
2) произведение двух четных (нечетных) функций есть функция четная.
Следовательно, тригонометрический ряд Фурье на отрезке будет иметь вид
для четной функции:
для нечетной функции:
Ряд (16) не содержит синусов кратных углов, то есть в ряд Фурье четной функции входят только четные функции и свободный член. Ряд (17) не содержит косинусов кратных углов, то есть в ряд Фурье нечетной функции входят только нечетные функции [8].
Определение. Ряды
являются частями полного ряда Фурье и называются неполными тригонометрическими рядами Фурье.
Если функция разлагается в неполный тригонометрический ряд (16) (или (17)), то говорят, что она разлагается в тригонометрический ряд Фурье по косинусам (или по синусам).
1.6. Разложение в ряд Фурье непериодической функции
1.6.1. Разложение в ряд Фурье функций на
Получившуюся в результате замены функцию можно разложить на в ряд Фурье:
Сделаем обратную замену ⇒ Получим
Ряд (18) – ряд Фурье по основной тригонометрической системе функций
Таким образом, получили, что если функция задана на отрезке и удовлетворяет на этом отрезке условиям теоремы Дирихле, то она может быть разложена в тригонометрический ряд Фурье (18) по тригонометрической системе функций (20) [8].
для нечетной функции
1.6.2. Разложение в ряд Фурье функций на
1) Аналогично можно разложить в ряд Фурье функцию, заданную на отрезке
2) Так как разложение функции на отрезке предполагает ее продолжение на отрезок произвольным образом, то и ряд Фурье для функции не будет единственным [3].
1.6.3. Разложение в ряд Фурье функций на
Пусть функция задана на произвольном отрезке длины и удовлетворяет на нем условиям теоремы Дирихле.
Поэтому коэффициенты Фурье для полученного продолжения функции можно найти по формулам
2. Практическое применение рядов Фурье
2.1. Задачи на разложение функций в ряд Фурье и их решение
В тригонометрический ряд Фурье требуется разложить функцию, являющуюся периодическим продолжением заданной на отрезке функции. Для этого необходимо пользоваться алгоритмом разложения периодической функции в ряд Фурье.
Алгоритм разложения периодической функции в ряд Фурье:
1) Построить график заданной функции и ее периодического продолжения;
2) Установить период заданной функции;
3) Определить функция четная, нечетная или общего вида;
4) Проверить выполнимость условий теоремы Дирихле;
5) Составить формальную запись ряда Фурье, порожденного данной функцией;
6) Вычислить коэффициенты Фурье;
7) Записать ряд Фурье для заданной функции, используя коэффициенты ряда Фурье (п.4).
1) Построим график заданной функции и его периодическое продолжение.