Для чего нужен треугольник паскаля
Для чего нужен треугольник паскаля
Треугольник Паскаля
Автор работы награжден дипломом победителя III степени
Познакомиться с таким математическим объектом, как треугольник Паскаля
Пополнить запас научных знаний.
Продолжить знакомство с основными историческими этапами возникновения и развития математической науки, судьбами открытий, именами людей, творивших науку. В первую очередь с биографией ученого Блеза Паскаля.
Самостоятельно попытаться составить данный треугольник.
Рассмотреть свойства треугольника Паскаля.
Определить значимость открытия треугольника Паскаля.
Сформулировать вывод и итоги исследования.
Треугольник Паскаля обладает рядом замечательных свойств, поэтому и носит имя одного из выдающихся людей.
Актуальность данной работы не вызывает сомнения, поскольку обусловлена, с одной стороны большим интересом к теме «Треугольник Паскаля» в современной науке, с другой стороны, её недостаточной разработанностью.
Навыки решения задач с применением треугольника Паскаля помогут в рамках изучения школьного курса математики, при решении олимпиадных задач.
Сбор первоначальных сведений о треугольнике в энциклопедической и учебно-научной литературе.
Построение треугольник Паскаля.
Выявление «волшебных» свойств чисел треугольника.
Изучение возможностей применения треугольника Паскаля.
Формулирование итогов и выводов.
аналитико-статистическая работа со справочной, научно-познавательной и специальной литературой;
1.Биография Блеза Паскаля
Прогресс человечества во многом связан с открытиями, сделанными гениями.
Род Паскалей отличали незаурядные способности, а Блеза одаренность посетила с раннего детства. Этьен Паскаль уделил много внимания развитию умственных способностей сына и уже в 16 лет Блез сочинил труд под названием «Опыт о конических сечениях» в котором содержалась теорема известная, как теорема Паскаля.
Вклад Паскаля в науках очень велик. Вот лишь некоторые из них: заложил основы современной теории вероятностей и математического анализа, сформулировал основной закон гидростатики, написал множество трудов по философии, изобрел шприц, создал гидравлический пресс и вычислительное устройство «Паскалин» (прототип калькулятора), изобрел тачку, придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.
Умер Блез Паскаль 19 августа 1662 года.
2.Определение и основные свойства треугольника Паскаля.
2.1 История треугольника.
Похожий треугольник представлен в качестве иллюстрации в книге китайского математика Яна Хуэя, изданной в 1303 году.
О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.
2.2 Построение треугольника Паскаля.
«Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В то же время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике» (Мартин Гарднер).
Треугольником Паскаля называется бесконечная треугольная таблица, в которой (рис.1):
на вершине и по боковым сторонам стоят единицы,
-каждое из остальных чисел равно сумме двух чисел, стоящих над ним в предшествующей строке.
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. Продолжать треугольник можно бесконечно.
2.3 Основные свойства треугольника Паскаля.
Для любой строки под номером n (n = 0, 1, 2…) верно:
Первое и последнее числа – 1; второе и предпоследнее – n.
Строки треугольника симметричны относительно вертикальной оси треугольника.
Сумма чисел n-й строки треугольника Паскаля равна (рис.2)
Четвертая диагональ – это «фигурные числа» в четырехмерном измерении. Это можно представить только в виртуальном мире. Один шар касается четырех, а те, в свою очередь, десяти…
Каждое число треугольника Паскаля равно сумме чисел предыдущей диагонали, стоящей над этим числом.
В каждой строке сумма чисел на нечётных местах равна сумме чисел на чётных местах.
Если номер строки – простое число, то все числа этой строки, кроме 1, делятся на это число.
Каждое число, уменьшенное на 1, равно сумме всех чисел, заполняющих параллелограмм, ограниченный правыми и левыми диагоналями, на пересечении которых стоит это число.
Бином Ньютона – возведение выражения (a + b) в степень. При возведении в степень получаются коэффициенты, равные числам в треугольнике Паскаля.
Сумма чисел n-й восходящей диагонали, проведенной через строку треугольника с номером n − 1, есть n-е число Фибоначчи (число равно сумме двух предыдущих чисел) (рис.5).
3. Применение треугольника Паскаля.
Где же применяется треугольник Паскаля?
При решении комбинаторных задач.
Треугольник Паскаля используется для решения различных задач в области физики:
принцип минимума потенциальной энергии;
материальные точки и центр тяжести;
центр тяжести системы двух материальных точек;
центр тяжести стержня с многими грузами;
невозможность вечного двигателя.
С появлением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении основ программирования.
Вот далеко не полный перечень свойств чисел треугольника Паскаля и его многочисленных применений.
4. Применение свойств треугольника Паскаля в решении математических задач.
Свойства треугольника Паскаля, наверное, были бы не столь значимы, если бы на их основе нельзя было решать математические задачи. Такие задачи можно встреть в ОГЭ, ЕГЭ и в олимпиадных задачах старшего школьного уровня. Треугольник Паскаля используется при решении комбинаторных задач, для решения различных задач в области физики. С построением вычислительных машин построение треугольника Паскаля стало излюбленной задачкой для начинающих при изучении программирования.
Найдите сумму первых 8 треугольных чисел.
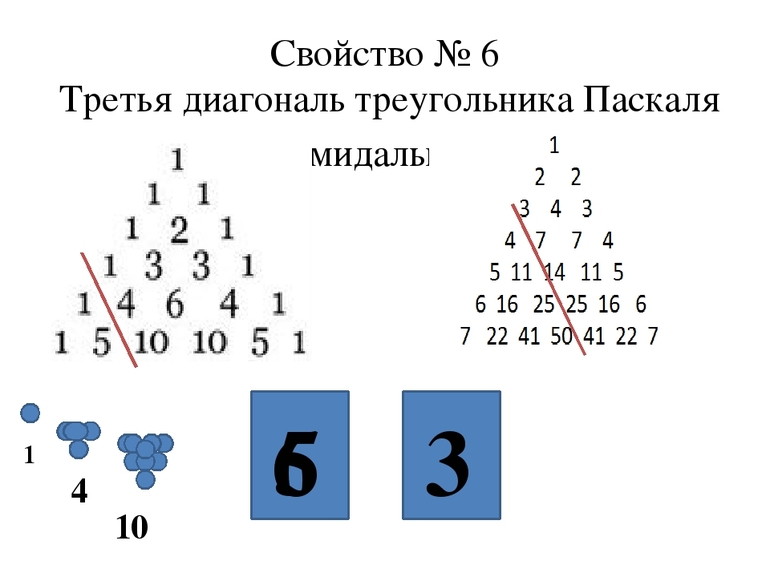
Найдем сумму первых восьми чисел 3 диагонали треугольника Паскаля. (рис.6) Получится 120.
Вася построил из шариков пирамиду. Известно, что на её строительство ушло 286 шариков, сколько «этажей» в Васиной пирамиде?
В данной задаче нам известно, что на строительство пирамиды ушло 286 шариков. Найдем решение с помощью треугольника Паскаля, в котором количество прямоугольников, пересеченных зеленой линией, будет наш ответ. (рис. 7)
В магазине «Теплица» продается 6 различных сортов помидор. Сколькими способами можно выбрать из них 3 сорта помидор?
В данной задаче нам даны различные сорта, поэтому повторений не будет и порядок выбора сортов нам неважен, нам важно количество, а именно 3. Найдем решение с помощью нашего треугольника Паскаля, в котором пересечении 3-й диагонали и 6 строки будет наш ответ (рис.8).
На плоскости даны 11 точек, из которых никакие три не лежат на одной прямой и никакие четыре не лежат на одной окружности. Сколько существует окружностей, каждая из которых проходит через три данные точки
Ответ находится на пересечении 11 ряда и 3 диагонали: Это число – 165 (рис.9).
Ответ: 165 окружностей.
Танк может двигаться по квадратам, видимым на карте, размером 4 на 4 только вправо или вниз. Он стоит в точке А. Из штаба пришло задание прибыть в точку В. Сколько маршрутов передвижения может использовать экипаж?
Решив задачу, мы замечаем, что полученные на «карте» числа образуют треугольник Паскаля. Таким образом, можно сделать вывод, что число в треугольнике Паскаля показывает количество способов передвижения от вершины треугольника до данного числа.
Из пункта А по сети дорог идет группа из человек. На каждом перекрестке, начиная с А, пришедшие туда люди делятся пополам – половина идет по направлению l, половина – по направлению m (рис.11). Сколько человек придет в пункты В, С, D, …, I соответственно?
Количество людей, пришедших в искомые точки соответствует числам n-ой строки. В данном случае, n = 7, следовательно¸ искомое количество людей на каждом перекрестке соответствует 7 строке треугольника Паскаля (рис.12).
Ответ: 1, 7, 21, 35, 35, 21, 7, 1.
В ходе исследования мы убедились, что треугольник Паскаля, несмотря на кажущуюся простоту, действительно обладает рядом замечательных свойств, знание которых будет полезно. Этот треугольник широко используется в математике для решения различных видов задач. Треугольник Паскаля имеет применение не только в математике, но и в физике, информатике.
Изучение темы «Треугольник Паскаля» оказалось очень интересной и необычной. Работа над проектом показала, что математика – это не только точная, но и красивая наука.
Гиндикин, С.Г. Рассказы о физиках и математиках/ С.Г.Гиндикин. – М.: Терра, 2013. – 480с.
Энциклопедия для детей Аванта+: В 57 т. Т. 11. Математика/ под ред. М. Аксёновой, В. Володина, М. Самсоновф – М.: Аванта+, 2003. — 688 с.
Корбалан, Ф. Мир математики: В 40 т. Т.1. Золотое сечение, математический язык красоты/ Пер. с исп. — М.: DeAgostini, 2014. — 164 с.: ил.
Гарднер, М. Математические новеллы. (Mathematics Games) / Пер. с англ. Ю.А.Данилова; под ред. Я.А. Смородинского — М.: Мир, 1974. — 456 с.
Основная формула
Строки треугольника обычно нумеруются, начиная со строки n = 0 в верхней части. Записи в каждой строке целочисленные и нумеруются слева, начиная с k = 0, обычно располагаются в шахматном порядке относительно чисел в соседних строчках. Построить фигуру можно следующим образом:
История открытия
Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».
Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.
Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.
Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.
Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.
На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.
В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).
Отличительные черты
Треугольник Паскаля и его свойства — тема довольно обширная. Главное, в нём содержится множество моделей чисел. Обзор следует начать с простого — ряды:
Диагонали треугольника содержат фигурные числа симплексов. Например:
Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.
Общие свойства
Образец, полученный путём раскраски только нечётных чисел, очень похож на фрактал, называемый треугольником Серпинского. Это сходство становится всё более точным, так как рассматривается больше строк в пределе, когда число рядов приближается к бесконечности, получающийся в результате шаблон представляет собой фигуру, предполагающую фиксированный периметр. В целом числа могут быть окрашены по-разному в зависимости от того, являются ли они кратными 3, 4 и т. д.
В треугольной части сетки количество кратчайших путей от заданного до верхнего угла треугольника является соответствующей записью в паскалевском треугольнике. На треугольной игровой доске Плинко это распределение должно давать вероятности выигрыша различных призов. Если строки треугольника выровнены по левому краю, диагональные полосы суммируются с числами Фибоначчи.
Количество элементов симплексов фигуры можно использовать в качестве справочной таблицы для количества элементов (рёбра и углы) в многогранниках (треугольник, тетраэдр, квадрат и куб).
Шаблон, созданный элементарным клеточным автоматом с использованием правила 60, является в точности паскалевским треугольником с биномиальными коэффициентами, приведёнными по модулю 2. Правило 102 также создаёт этот шаблон, когда завершающие нули опущены. Правило 90 создаёт тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках. Фигура может быть расширена до отрицательных номеров строк.
Секреты треугольника
Конечно, сейчас большинство расчётов для решения задач не в классе можно сделать с помощью онлайн-калькулятора. Как пользоваться треугольником Паскаля и для чего он нужен, обычно рассказывают в школьном курсе математики. Однако его применение может быть гораздо шире, чем принято думать.
Начать следует со скрытых последовательностей. Первые два столбца фигуры не слишком интересны — это только цифры и натуральные числа. Следующий столбец — треугольные числа. Можно думать о них, как о серии точек, необходимых для создания групп треугольников разных размеров.
Точно так же четвёртый столбец — это тетраэдрические числа или треугольные пирамидальные. Как следует из их названия, они представляют собой раскладку точек, необходимых для создания пирамид с треугольными основаниями.
Столбцы строят таким образом, чтобы описывать «симплексы», которые являются просто экстраполяциями идеи тетраэдра в произвольные измерения. Следующий столбец — это 5-симплексные числа, затем 6-симплексные числа и так далее.
Полномочия двойки
Если суммировать каждую строку, получатся степени основания 2 начиная с 2⁰ = 1. Если изобразить это в таблице, то получится следующее:
| 1 | ||||||||||||||
| 1 | + | 1 | = | 2 | ||||||||||
| 1 | + | 2 | + | 1 | = | 4 | ||||||||
| 1 | + | 3 | + | 3 | + | 1 | = | 8 | ||||||
| 1 | + | 4 | + | 6 | + | 4 | + | 1 | = | 16 | ||||
| 1 | + | 5 | + | 10 | + | 10 | + | 5 | + | 1 | = | 32 | ||
| 1 | + | 6 | + | 15 | + | 20 | + | 15 | + | 6 | + | 1 | = | 64 |
Суммирование строк показывает силы базы 2.
Силы одиннадцати
Треугольник также показывает силы основания 11. Всё, что нужно сделать, это сложить числа в каждом ряду вместе. Как показывает исследовательский опыт, этого достаточно только для первых пяти строк. Сложности начинаются, когда записи состоят из двузначных чисел. Например:
| 1 | = | 11° |
| 11 | = | 11¹ |
| 121 | = | 11² |
| 1331 | = | 11³ |
Оказывается, всё, что нужно сделать — перенести десятки на одно число слева.
Совершенные квадраты
Комбинаторные варианты
Чтобы раскрыть скрытую последовательность Фибоначчи, которая на первый взгляд может отсутствовать, нужно суммировать диагонали лево-выровненного паскалевского треугольника. Первые 7 чисел в последовательности Фибоначчи: 1, 1, 2, 3, 5, 8, 13… найдены. Используя исходную ориентацию, следует заштриховать все нечётные числа, и получится изображение, похожее на знаменитый фрактальный треугольник Серпинского.
Возможно, самое интересное соотношение, найденное в треугольнике — это то, как можно использовать его для поиска комбинаторных чисел, поскольку его первые шесть строк написаны с помощью комбинаторной записи. Поэтому, если нужно рассчитать 4, стоит выбрать 2, затем максимально внимательно посмотреть на пятую строку, третью запись (поскольку счёт с нуля), и будет найден ответ.
Действия с биномами
Например, есть бином (x + y), и стоит задача повысить его до степени, такой как 2 или 3. Обычно нужно пройти долгий процесс умножения (x + y)² = (x + y)(x + y) и т. д. Если воспользоваться треугольником, решение будет найдено гораздо быстрее. К примеру, нужно расширить (x + y)³. Поскольку следует повышать (x + y) до третьей степени, то необходимо использовать значения в четвёртом ряду фигуры Паскаля (в качестве коэффициентов расширения). Затем заполнить значения x и y. Получится следующее: 1 x³ + 3 x²y + 3 xy² + 1 y³. Степень каждого члена соответствует степени, до которой возводится (x + y).
Биномиальное распределение описывает распределение вероятностей на основе экспериментов, которые можно разделить на группы с двумя возможными исходами. Самый классический пример этого — бросание монеты. Например, есть задача выбросить «решку» — успех с вероятностью p. Тогда выпадение «орла» является случаем «неудачи» и имеет вероятность дополнения 1 – p.
Глава 10. Треугольник Паскаля
Построение и некоторые свойства треугольника Паскаля
В верхней строчке треугольника располагается одинокая единица. В остальных строках каждое число является суммой двух своих соседей этажом выше — слева и справа. Если какой-то из соседей отсутствует, он считается равным нулю. Треугольник бесконечно простирается вниз; мы приводим лишь восемь верхних строчек: 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 …
Назовём лишь некоторые факты, относящиеся к треугольнику Паскаля.
Треугольник Паскаля и числа Фибоначчи
Треугольники Паскаля и Серпинского
Если раскрасить нечётные числа в треугольнике Паскаля в один цвет, а чётные — в другой, получится такая картина (на рисунке 10.1. «Треугольник Паскаля — Серпинского» указанным образом раскрашены числа в первых 128 строчках):
Похожее изображение можно построить следующим образом. В закрашенном треугольнике перекрасим в другой цвет его серединный треугольник (образованный серединами сторон исходного). Три маленьких треугольника, расположенные по углам большого, останутся закрашенными в прежний цвет. Поступим с каждым из них точно так же, как мы поступили с большим, то есть перекрасим в каждом серединный треугольник. То же самое сделаем с оставшимися треугольниками старого цвета. Если эту процедуру проделывать до бесконечности, на месте исходного треугольника останется двухцветная фигура. Та её часть, которая не перекрашена, называется треугольником Серпинского. Несколько первых этапов построения треугольника Серпинского показаны на рисунке 10.2. «Построение треугольника Серпинского».
Математика, которая мне нравится
Математика для школьников и студентов, обучение и образование
Чудесный треугольник Блеза Паскаля
Все узнают о треугольнике Паскаля в юности. Но, видимо, узнают не все чудеса, которые содержит треугольник. В самом деле, мы до сих пор открываем новые вещи!
Строится треугольник довольно легко: по внешним краям нужно поставить единицы, а каждое число внутри равно сумме двух чисел, которые стоят над ним. Так, третье число в шестой строке равно 


Внимание! На самом деле мы будем говорить, что 

Зная правило сложения, можно продолжать бесконечно: вы можете написать столько строк, сколько позволит ваше терпение.
Первые 10 строк треугольника Паскаля
Паскаль ввел свой треугольник в 1653 г. в Traité du triangle arithmétique как часть задачи исследования вероятностей и для вычислений. Задачи были примерно такие: “Если я хочу выбрать двух человек из четырех данных, сколько существует возможных пар?’’ или “Какова вероятность выпадения фулл-хауса (примеч. в покере три карты одного достоинства и две другого), когда раздается по пять карт из колоды, которая хорошо перемешана?’’ Паскаль и Ферма в основном обсуждали вероятность в письмах, которыми они обменивались в то время. Вы можете увидеть исходный треугольник Паскаля здесь.
Каким образом треугольник связан с вероятностью? Ну, если вы хотите выбрать 






На первый взгляд, кажется довольно непонятным, почему треугольник дает правильный ответ на этот вопрос. Может также показаться странным, что мы должны всегда начинать с нуля, чтобы заставить его работать. Чтобы увидеть, что все это совершенно верно, мы сделаем два замечания.
Во-первых, если у вас есть группа объектов, каким количеством способов вы можете выбрать нуль объектов из них? Есть ровно один способ выбрать нуль объектов, а именно: просто заявив, что вы не берете ни одного из них. Кроме того, у вас есть только один способ выбрать все объекты. И это как раз соответствует единицам на двух концах каждой строки.
Во-вторых, если мы хотим выбрать 






Короче говоря, чтобы получить число способов выбора 





Мы уже знаем, что треугольник полностью определяется расположением единиц по его сторонам и правилом сложения. Так как эти свойства применимы также к ответу на вопрос о количестве вариантов выбора объектов, треугольник должен и здесь давать правильный ответ.
Возможность сделать такие расчеты неоценима во множестве случаев. Поэтому мало удивляет, что Паскаль не был первым. Данные числа были рассмотрены индийскими, китайскими и иранскими математиками в разное время, начиная с момента более чем тысячелетней давности. И, конечно, все узнают треугольник Яна Хуэя, 1303 г.:
Забавно, даже не будучи в состоянии различить числа, вы можете найти опечатку в этом треугольнике, которому больше 700 лет! Подсказка: правило сложения делает треугольник Паскаля симметричным относительно вертикальной прямой, проходящей через его вершину. Если вы посмотрите внимательно, в треугольнике Ян Хуэя эта симметрия в одном месте нарушается.
В треугольнике много чудесного. Где же чудеса? Некоторые из них легко заметить. Если вы сложите числа в 



Несколько более интересным является тот факт, что если вы сложите числа, стоящие в треугольнике по диагоналям, получится последовательность чисел Фибоначчи. А последовательность чисел Фибоначчи сама содержит множество сюрпризов.
Недавно нечто удивительное и новое было обнаружено в треугольнике Паскаля. Как мы видели, если сложить числа, стоящие в строке треугольника, происходит что-то интересное. Этот факт о суммах так же стар, как и сам треугольник. Однако до 2012 г., до Харлана Бразерса, никто не пытался выяснить, что произойдет, если перемножить числа в каждой строке.
Давайте обозначим через 




Т. е. для каждой строки он рассмотрел дробь, числитель которой равен произведению всех чисел в строке, стоящей под ней, и в строке, стоящей над ней, а знаменатель — произведению всех чисел в данной строке в квадрате.
И вот удивительная вещь: когда 






Вот такая симпатичная анимация Ричарда Грина наглядно показывает результат Харлана Бразерса:
Существует еще одно чудо в треугольнике, которое каждый должен знать. Давайте каждое число в треугольнике покрасим в один из двух цветов, в зависимости от того, является оно четным или нечетным. Например, мы могли бы покрасить четные числа белым, а нечетные — синим. Если мы сделаем это для первых 500 строк треугольника, получим вот такую закономерность:
Это известный фрактал, известный как треугольник Серпинского! Это приводит к разного рода вопросам. Число четное или нечетное, если оно при делении на 





Существует забавное приложение, которое позволяет увидеть, что происходит, если менять число, на которое вы делите (также называемое модулем). Полезный совет: когда вы используете приложение, нажмите на маленький символ “плюс’’, чтобы использовать более детальную версию управления. В треугольнике Паскаля есть множество других удивительных вещей. Для начала, если вы заинтересовались этим, подойдет веб-сайт mathforum.org. Ну а более, скажем, эксцентричные, вещи, которые можно найти в треугольнике, имеются здесь.
Комментариев: 7
1 Murad:
Грубые ошибки – абсурды, допущенные предками и нами
2 Корнеев В.Ф.:
А как вам нравится следующий критерий простоты числа:
число тогда и только тогда простое, когда все числа треугольника Паскаля (единицы не в счёт) с номером строки этого числа делятся на это число.
Так 9 не простое число, потому что 84 не делится на 9. А 7 – простое, потому что все числа 7-ой строки делятся на 7.
Twilight_Sun Reply:
Февраль 8th, 2015 at 0:48
Как-то слишком уж очевидно доказывается : )
Корнеев В.Ф. Reply:
Февраль 8th, 2015 at 8:26
3 Murad:
Каждое целое число куб, поэтому10ст.3n = 500 x 10 ст.3(n-1) + 500 x10ст.3(n-1), где 500 x 103(n-1)нечетных и столько же четных. Целые числа начинаются с 1, а их номера с 0.
4 Вадим:
5 Сергей:
См. о треугольнике Паскаля самое впечатляющее и до 1981 года никому неведомое: Абачиев С. К., Стахов А. П. Треугольник Паскаля и спектр арифметик для цифровых информационных технологий.// Интернет-журнал №Науковедение”. – М.: ИГУПиТ, 2012, Вып 4.