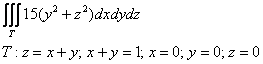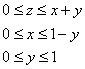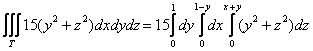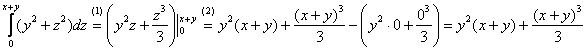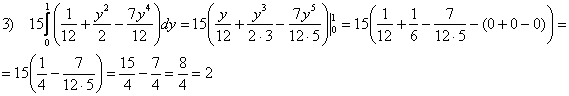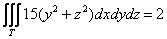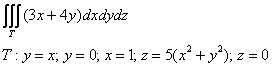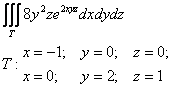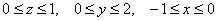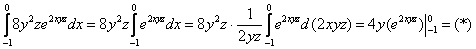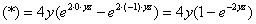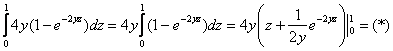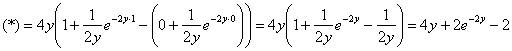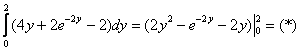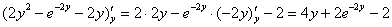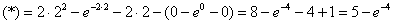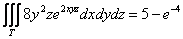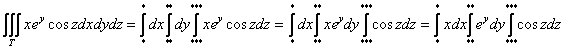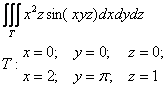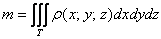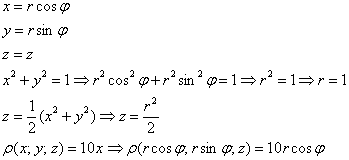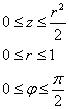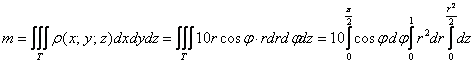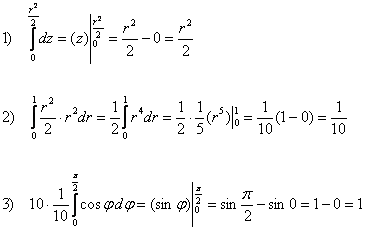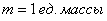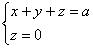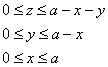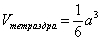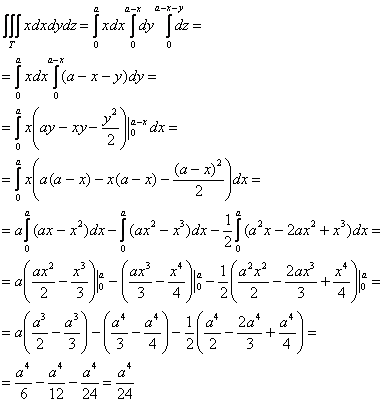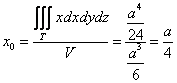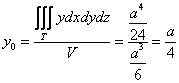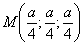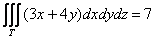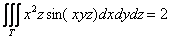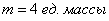Для чего нужен тройной интеграл

18.04.202221.04.2022 admin 0 Comments

Вычисление тройных интегралов: теория и примеры

Понятие тройного интеграла

Записывается тройной интеграл так:

Здесь V – пространственная (трёхмерная) фигура, ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.

Если функция f(M) = f(x, y, z) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом.

Вычисление тройного интеграла путём уменьшения кратности

Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов меньшей кратности.

Мы будем рассматривать только правильные области.

Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:

Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три определённых интеграла.

Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три «вложенных» интеграла можно записать так:

Из этой записи уже однозначно видно, что:

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу

—

последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.

Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла:

Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.

Пример 2. Вычислить тройной интеграл

Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:

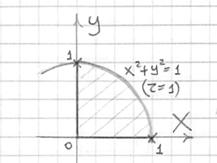
Пример 3. Вычислить тройной интеграл

Сводим данный тройной интеграл к последовательности трёх определённых интегралов:

Ответ: данный тройной интеграл равен 1/8.

Вычислить тройной интеграл самостоятельно, а затем посмотреть решение

Пример 4. Вычислить тройной интеграл

Расстановка пределов интегрирования при переходе к последовательности трёх интегралов

Начнём с примера «пострашнее», чтобы почувствовать «обстановку, приближенную к боевой».

Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:

Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:

Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:

Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:

Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:

Пример 6. Вычислить тройной интеграл

Решение. «Курортный» пример по сравнению с примером 5, так как пределы интегрирования по «игрек» и «зет» определены однозначно. Но придётся разобраться с пределами интегрирования по «иксу». Проекцией области интегрирования на плоскость xOy является трапеция ABCD.

Ответ: данный тройной интеграл равен 43.

Пример 7. Вычислить тройной интеграл

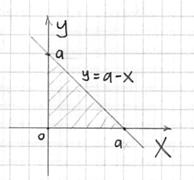
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.

Сведём данный тройной интеграл к последовательности трёх определённых интегралов:

Ответ: данный тройной интеграл равен 2.

Замена переменных в тройном интеграле и цилиндрические координаты

Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:

То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:

Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:

Пример 8. Вычислить тройной интеграл

Ответ: данный тройной интеграл равен π/6.

Тройной интеграл в сферических координатах

Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями

Элемент объёма в сферических координатах выражается следующим образом:

Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:

Пример 9. Вычислить тройной интеграл

Учитывая, что , получаем

Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому

Приложения тройного интеграла

Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:

Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:

Пример 10. Вычислить объём тела, ограниченного поверхностями , , .

Таким образом, записываем тройной интеграл в цилиндрических координатах и вычисляем его:

Источник

Примеры решений произвольных тройных интегралов.
Физические приложения тройного интеграла

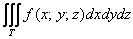
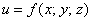
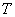
Во 2-й части урока мы отработаем технику решения произвольных тройных интегралов , у которых подынтегральная функция трёх переменных в общем случае отлична от константы и непрерывна в области ; а также познакомимся с физическими приложениями тройного интеграла

Вновь прибывшим посетителям рекомендую начать с 1-й части, где мы рассмотрели основные понятия и задачу нахождения объема тела с помощью тройного интеграла. Остальным же предлагаю немного повторить производные функции трёх переменных, поскольку в примерах данной статьи мы будем использовать обратную операцию – частное интегрирование функции .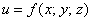

Кроме того, есть ещё один немаловажный момент: если у Вас неважное самочувствие, то прочтение этой странички по возможности лучше отложить. И дело не только в том, что сейчас возрастёт сложность вычислений – у большинства тройных интегралов нет надёжных способов ручной проверки, поэтому к их решению крайне нежелательно приступать в утомлённом состоянии. При пониженном тонусе целесообразно порешать что-нибудь попроще либо просто отдохнуть (я терпелив, подожду =)), чтобы в другой раз со свежей головой продолжить расправу над тройными интегралами:

Вычислить тройной интеграл

На практике тело также обозначают буквой 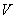, но это не очень хороший вариант, ввиду того, «вэ» «зарезервировано» под обозначение объёма.

Сразу скажу, чего делать НЕ НАДО. Не нужно пользоваться свойствами линейности и представлять интеграл в виде 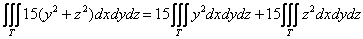. Хотя если очень хочется, то можно. В конце концов, есть и небольшой плюс – запись будет хоть и длинной, но зато менее загромождённой. Но такой подход всё-таки не стандартен.

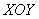
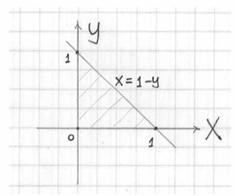
В алгоритме решения новизны будет немного. Сначала нужно разобраться с областью интегрирования. Проекция тела на плоскость представляет собой до боли знакомый треугольник:

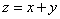
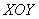
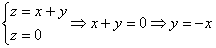
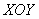
Сверху тело ограничено плоскостью , которая проходит через начало координат. Предварительно, к слову, нужно обязательно проверить (мысленно либо на черновике), не «срезает» ли эта плоскость часть треугольника. Для этого находим её линию пересечения с координатной плоскостью , т.е. решаем простейшую систему: – нет, данная прямая (на чертеже отсутствует) «проходит мимо», и проекция тела на плоскость действительно представляет собой треугольник.

Не сложен здесь и пространственный чертёж: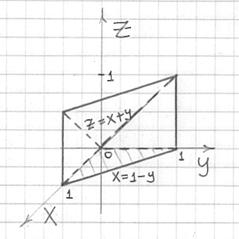

В действительности можно было ограничиться только им, поскольку проекция очень простая. …Ну, или только чертежом проекции, так как тело тоже простое =) Однако совсем ничего не чертить, напоминаю – плохой выбор.

Выберем следующий порядок обхода тела:

И перейдём к повторным интегралам:

Актуализируем следующее элементарное правило:

Когда функция 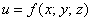интегрируется по какой-либо переменной, то два других аргумента считаются константами. То есть принцип точно такой же, как и при нахождении частных производных от функции трёх переменных, что естественно.

Разбираемся с интегралами:

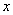
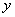
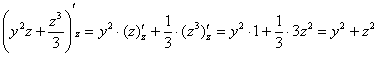
(1) При интегрировании по «зет» и считаются константами. В данном случае присутствует только «игрек», но это не меняет дела. Советую всегда мысленно либо на черновике выполнять проверку. Найдём частную производную по «зет»:
, что и требовалось проверить.

(2) Теперь используем формулу Ньютона-Лейбница: сначала ВМЕСТО «зет» подставляем верхний предел интегрирования 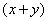, затем – нижний предел (ноль). В результате буквы «зет» остаться не должно!

Сносим трофей в следующий интеграл. По существу, решение свелось к двум переменным и к двойному интегралу:

(1) Используем свойства линейности интеграла, принимая во внимание тот факт, что «игрек» считается константой. Следует отметить, что не возбраняется оставить интеграл единым, раскрыть скобки и привести подобные слагаемые, но это менее рациональный способ (можете попробовать).

(2) Используем метод подведения под знак дифференциала. Если рассуждения воспринимаются совсем тяжело, мысленно замените «игрек» каким-нибудь конкретным числом, например, «пятёркой».

(3) Интегрируем по «икс» и выполняем проверку: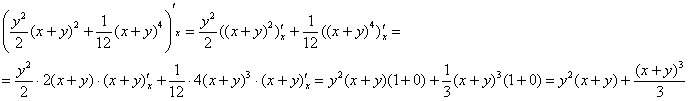

(4) Используем формулу Ньютона-Лейбница. Сначала ВМЕСТО «икс» (переменной, по которой проводилось интегрирование) подставляем 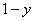, затем – ноль. После подстановок буквы «икс» остаться не должно!

Причёсываем результат и сносим его в последний интеграл, не теряя находящуюся там константу:

Ответ:

Результат безразмерен – просто число и всё.

Следующий пример для самостоятельного решения:

Вычислить тройной интеграл

Примерный образец оформления задачи в конце урока.

До сих пор мы рассматривали два способа решения – это проецирование на плоскость и выбор порядка обхода проекции. Но на самом деле комбинаций больше – тело можно спроецировать на любую из 3 координатных плоскостей и каждую проекцию обойти 2 путями. Таким образом, получается 6 способов решения. И логично предположить, что в общем случае некоторые из них проще, а некоторые – труднее.

Наверняка многие обратили внимание, что в Примере № 13 я выбрал более редкий порядок обхода проекции, хотя ничто не мешало пойти «обычным» путём. Это не случайность.
В результате нахождения интеграла получена сумма , в которой чуть выгоднее считать константой именно «игрек», что при прочих равных условиях (из уравнения прямой одинаково легко выразить ) упрощает решение. А в некоторых задачах выбор порядка интегрирования и вовсе становится ОЧЕНЬ важным:

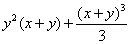
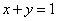
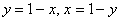
Вычислить тройной интеграл

Решение: область интегрирования ограничена шестью плоскостями и представляет собой прямоугольный параллелепипед: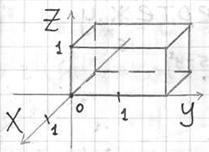

У незамысловатых областей можно не обращать внимания на проекцию и придерживаться следующего правила: обход тела осуществляется в направлениях координатных осей. Пределы интегрирования здесь очевидны

Но вот с порядком обхода не всё так просто. Если выбрать традиционный путь и сначала интегрировать по «зет», то получается неприятный интеграл 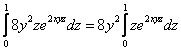, который нужно брать по частям. Аналогичная история, если интегрировать по «игрек»: , тут даже дважды по частям.

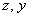
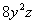
Наиболее выгодным путём является первоочередное интегрирование по «икс», в этом случае переменные , а значит, и множитель считаются константами:

Перед тем, как подставить пределы интегрирования, не помешает проверка:
– получена исходная подынтегральная функция.

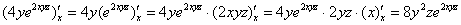
Буква «икс» испарилась, как оно и должно быть.

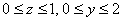
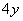
Осталось 2 направления обхода , и следующий интеграл рациональнее взять по «зет» чтобы множитель считался константой:

Промежуточная проверка: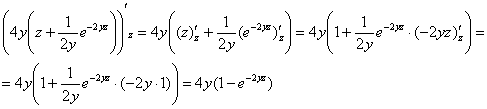

Гуд.

В качестве дополнительного контроля снова смотрим, исчезла ли после подстановки переменная, по которой интегрировали («зет»).

И, наконец, оставшееся направление обхода 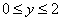и оставшийся интеграл:

Проверка:

При подстановках следует проявлять повышенное внимание, так, например, при подстановке нуля в выражение 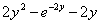второе слагаемое можно машинально счесть за ноль.

На чистовике, конечно же, не нужно всё расписывать так подробно, анализ порядка интегрирования и промежуточные проверки осуществляются мысленно либо на черновике. Решение оформляется стандартно в 3 пункта, но читатели с хорошим уровнем подготовки могут записать его и «одной строкой»:

Ответ:

Наверное, это понятно, но на всякий случай закомментирую: буквенные множители-константы следует перемещать справа налево последовательно и без «перескоков» – до тех пор, пока каждая буква «не встретит свой интеграл». Условный пример:

Аналогичное задание для самостоятельного решения:

Вычислить тройной интеграл

Примерный образец чистового оформления задачи в конце урока.

Чем дальше, тем интереснее:

Физические приложения тройного интеграла

Но сначала разомнёмся физически, тело – в дело =) Пожалуйста, встаньте и найдите какой-нибудь пакет или мешок. Можно коробку. Теперь походим по квартире, ну или по улице и наведём порядок. А именно, наполним тару мусором. …Очень хорошо, молодцы. В результате ваших трудов получено ограниченное тело неоднородной плотности. Как говорится, есть бумажка, а есть жестяная крышка. Воздух, кстати, тоже обладает вполне определённой плотностью. Напоминаю, что физическая плотность – есть отношение массы к объёму, например, 100 грамм на кубический метр.

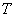
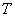
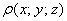
Ставим мешок рядышком и читаем дальше. Рассмотрим неоднородное (переменной плотности) тело . Если известна непрерывная в области функция плотности тела, то его масса равна следующему тройному интегралу:

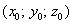
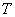
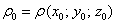
Возможно, не всем понятен смысл функции плотности. Поясняю: если взять произвольную точку , принадлежащую телу , то значение функции будет равно плотности тела в данной точке.

Только не стОит находить функцию 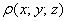для пакета с мусором, иначе шнобелевская премия обеспечена =) …Хотя, с другой стороны нашлись же энтузиасты оценить суммарную площадь поверхности индийских слонов и создать математическую модель пивной пены.

Однако разрядились, и хватит. Разберём несколько тематических задач:

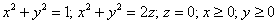
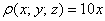
Вычислить массу неоднородного тела, ограниченного поверхностями , если известна функция его плотности .

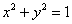
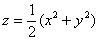
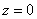
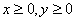
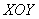
Решение: искомое тело ограничено цилиндром сбоку, эллиптическим параболоидом – сверху и плоскостью – снизу. Дополнительные условия «загоняют нас» в 1-й октант, и проекция тела на плоскость представляет собой соответствующую «четвертинку» единичного круга:

Аналитическим методом уточним высоту, на которой параболоид пересекает цилиндр:
и выполним пространственный чертёж:

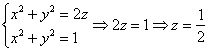
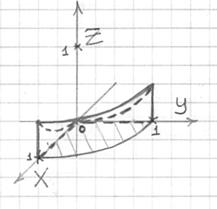
Проекция сразу же наводит на мысль о переходе к цилиндрической системе координат:

Порядок обхода тела очевиден:

Таким образом:

Вычисления элементарны:

Ответ:

Следующий пример для самостоятельного решения:

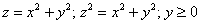
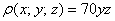
Вычислить массу неоднородного тела, ограниченного поверхностями , если известна функция его плотности .

Краткое решение в конце урока

И старая песня о главном:

Центр тяжести тела

Подобно тому, как задача о вычислении центра тяжести плоской фигуры вычислялась с помощью двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным способом с помощью тройного интеграла.

Что такое центр тяжести тела, довольно удачно объяснил ещё Архимед. Если тело подвесить на нить за центр тяжести, то оно будет сохранять равновесие в любом положении (как бы мы его предварительно ни повернули). В известной степени не реализуемо (таки центр тяжести внутри тела), но зато очень понятно. И вполне в стиле древнегреческого учёного, который просил дать ему точку опоры, чтобы с помощью рычага перевернуть Землю.

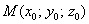
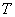
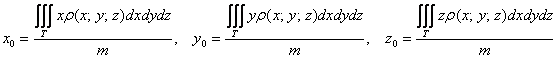
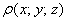
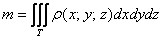
Центр тяжести неоднородного тела рассчитывается по формулам:

, где – функция плотности тела, а – масса тела.

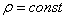
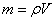
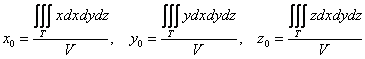
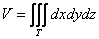
Если тело однородно (золотое, серебряное, платиновое и т.д.), то формулы упрощаются. Так как плотность постоянна, и масса – есть произведение плотности на объём, получаем:
, а объём тела рассчитывается (ещё не забыли? =)) с помощью тройного интеграла .

Для центра тяжести однородного тела справедливы следующие утверждения:

– если у тела есть центр симметрии, то он является центром тяжести (простейший пример – центр шара);

– если у тела существует линия симметрии, то центр тяжести обязательно принадлежит данной линии;

– если у тела есть плоскость симметрии, то центр тяжести непременно лежит в этой плоскости.

Как видите, практически полная аналогия с центром тяжести плоской фигуры.

Ну и, само собой, не могу не порадовать вас заключительной задачей:

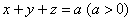
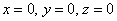
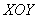
Найти центр тяжести однородного тела, ограниченного поверхностями , . Выполнить чертежи данного тела и его проекции на плоскость .

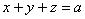
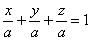
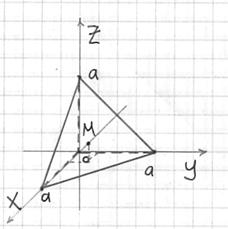
Решение: искомое тело ограничено координатными плоскостями и плоскостью , которую в целях последующего построения удобно представить в отрезках: . Выберем «а» за единицу масштаба и выполним трёхмерный чертёж:

На чертеже уже поставлена готовая точка центра тяжести, однако, пока мы её не знаем.

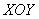
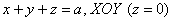
Проекция тела на плоскость очевидна, но, тем не менее, напомню, как её найти аналитически – ведь такие простые случаи встречаются далеко не всегда. Чтобы найти прямую, по которой пересекаются плоскости нужно решить систему:

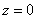
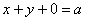
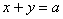
Подставляем значение в 1-е уравнение: и получаем уравнение «плоской» прямой:

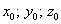
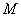
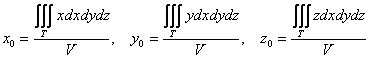
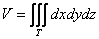
Координаты центра тяжести тела вычислим по формулам
, где – объём тела.

Выберем «классический» порядок обхода:

1) Сначала вычислим объём тела. Его, кстати, можно узнать заранее, пользуясь известной задачей геометрии об объёме тетраэдра. Объём тетраэдра равен 1/6-й объёма прямоугольного параллелепипеда, построенного на его трёх смежных рёбрах. В нашем случае параллелепипед представляет собой куб с ребром «а», и соответственно:

Осталось аккуратно провести чистовые вычисления (желающие могут потренироваться и выполнить их самостоятельно). В примерах с громоздкими преобразованиями рекомендую записывать решение столбиком – меньше шансов запутаться:

2) Вычислим «иксовый» интеграл:

Таким образом, «иксовая» координата центра тяжести:

Ну что же, выглядит правдоподобно, по крайне мере, мы «попали внутрь тела».

Ввиду симметрии тетраэдра две другие координаты должны получиться такими же. Теперь ошибочный ответ практически исключён!

3) Следующая «простыня»:

В результате:

4) И заключительный, более короткий интеграл:

Отмечаем на чертеже найденную точку центра тяжести и её же записываем в
ответ:

Осталось взять мешок с мусором и чувством глубокого морального удовлетворения выбросить его… нет, в окно не надо =)

Что осталось за кадром? В сетку урока не попала редко встречающая на практике сферическая система координат, в которой положение любой точки пространства однозначно определяется одним расстоянием и двумя углами. И до сферических координат у меня таки дошли пальцы в статье Дивергенция векторного поля.

Вы постоянно сетовали на простоту примеров, и поэтому я просто не мог вам не рассказать о криволинейных и поверхностных интегралах, а также основах векторного анализа.

Пример 14: Решение: изобразим проекцию данного тела на плоскость :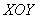

Сверху тело ограничено эллиптическим параболоидом .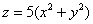
Выберем следующий порядок обхода: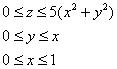

Таким образом: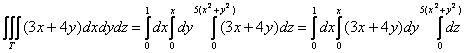

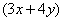
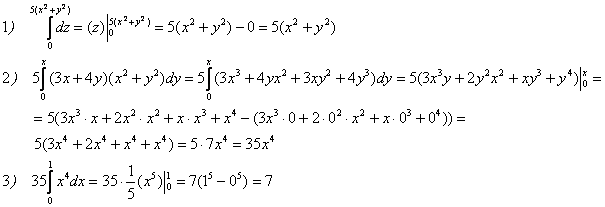
Примечание: в «зетовом» интеграле сумма считается константой, поэтому её удобно сразу вынести в следующий интеграл.

Ответ:

Пример 16: Решение: выполним чертёж: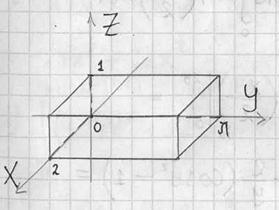

Выберем следующий порядок обхода тела: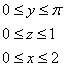

Таким образом: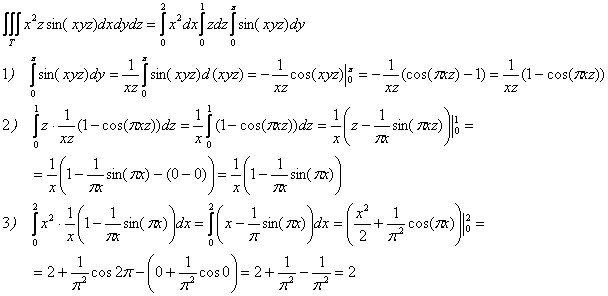

Ответ:

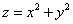
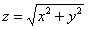
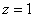
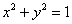
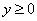
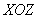
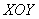
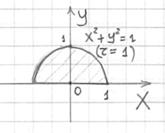
Пример 18: Решение: искомое тело ограничено эллиптическим параболоидом снизу и конической поверхностью – сверху; параболоид и конус пересекаются в плоскости по окружности (выкладки и чертёж – см. в Примере № 9 страницы Тройные интегралы). Поскольку , то речь идёт о правом (относительно плоскости ) полупространстве, и проекцией тела на плоскость является верхний полукруг единичного радиуса:

Массу тела вычислим с помощью тройного интеграла, используя цилиндрическую систему координат: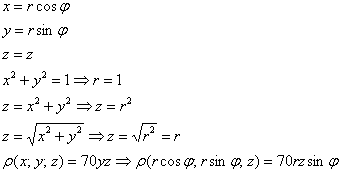

Порядок обхода тела: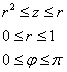

Таким образом:

Ответ: