Для чего нужна дискретная математика
Почему школам важно уделять больше времени изучению дискретной математики
Автор материала приводит аргументы в пользу изучения дискретной математики на этапе школьного образования.
Большинство программ по математике [в США] для средних и старших классов следуют четко прописанной схеме:
Предалгебраические задачи → Алгебра 1 → Геометрия → Алгебра 2 → Тригонометрия/начала матанализа → Матанализ
В некоторых других школах предпочтение отдается более комплексному подходу, в рамках которого элементы алгебры, геометрии и тригонометрии подаются смешанно в течение 3-х или 4-х летнего курса. Однако обоим методикам недостает существенного акцента на дискретную математику и такие ее разделы, как комбинаторика, теория вероятности, теория чисел, теория множеств, логика, алгоритмы и теория графов. Дискретная математика очень мало фигурирует в большинстве «критически важных» промежуточных экзаменов средних и старших классов. Аналогично ситуация обстоит и с приемными экзаменами для вузов и колледжей, таких, как SAT. Из-за этого дискретной математике часто уделяется мало внимания.
Тем не менее эта область знаний в последние годы становится все более и более важным направлением. И на то есть целый ряд причин:
Дискретная математика играет существенную роль в изучении математики в колледжах, вузах и более высоких ступенях.
Дискретная математика наряду с численными методами и общей алгеброй входит в список фундаментальные компонентов математики вузовского уровня. Ученики, получившие солидный объем знаний по дискретной математике перед поступлением в колледж, получают существенное преимущество во время дальнейшей учебы.
Дискретная математика — это математика вычислительных процессов.
Все вычисления современной компьютерной науки практически полностью основаны на дискретной математике, и в частности, комбинаторике и теории графов. Это значит, что для изучения фундаментальных алгоритмов, используемых компьютерными программистами, студентам требуется иметь твердые знания в этих областях. Действительно, для получения диплома в области компьютерных наук в большинстве университетов предусмотрен соответствующий обязательный курс по дискретной математике.
Дискретная математика больше всего приближена к задачам реального мира.
Многие учащиеся часто задаются вопросами о том, где в реальной жизни им может пригодится традиционная высшая математика, то есть алгебра, геометрия, тригонометрия и другие ее направления. Часто, глядя на абстрактную природу этих предметов, они теряют к ним интерес. Дискретная математика, и в частности, комбинаторика и теория вероятности, позволяют ученикам даже уровня средней школы очень быстро прийти к изучению интересных и нетривиальных задач, имеющих прямое отношение к задачам реального мира.
Дискретная математика — популярное направление большинства математических соревнований средней и старшей школы.
Видные математические олимпиады вроде MATHCOUNTS (средняя школа) и American Mathematics Competitions (старшие классы) включают значительное количество заданий по дискретной математике. В более сложных соревнования для старшеклассников, таких, как AIME, количество задач увеличивается еще сильнее. Ученики, не имеющие соответствующей базы знаний будут иметь гораздо меньше шансов на успех в таких соревнованиях. Один известный преподаватель, занимающийся подготовкой учеников к MATHCOUNTS, даже уделяет половину времени подготовке к заданиям по комбинаторике и теории вероятности. Настолько он считает их важными.
Дискретная математика развивает логическое мышление и учит техникам доказательства.
Алгебра часто преподается в виде совокупности формул и алгоритмов, которые ученики должны запомнить. Например, формула корней квадратного уравнения, или решение систем линейных уравнений путем замены. Геометрия часто преподается как серия упражнений, доказывающих теоремы и объясняющих их суть, которые нередко предлагается заучить наизусть. Несмотря на несомненную важность изучения подобного материала, в целом он не очень хорошо способствует развитию творческого математического мышления учеников. В противовес этому, изучающие дискретную математику дети учатся мыслить гибко и творчески уже с самого начала. Количество формул, которые требуется знать наизусть, относительно невелико. В этой области знаний акцент делается скорее на потребность изучить некоторое количество фундаментальных понятий, которые впоследствие можно применять совершенно по-разному.
Дискретная математика — это весело.
Многие студенты, особенно одаренные и мотивированные находят алгебру, геометрию и даже методы матанализа скучными, не вызывающими живого интереса. Что же касается дискретной математики, то в ней такие темы встречаются редко. Когда мы интересуемся у учащихся их любимыми темами, большинство называет комбинаторику или теорию чисел. Самой непопулярной темой при этом оказывается геометрия. Иными словами, большинство студентов находят дискретную математику более интересной, чем алгебра или геометрия.
Исходя из всех этих аргументов, мы настоятельно рекомендуем строить программу так, чтобы после изучения геометрии, школы уделяли некоторое время ознакомлению учеников с элементарными идеями дискретной математики, и в частности, комбинаторики, теории вероятности и теории чисел.
Основы дискретной математики
Привет, хабр. В преддверии старта базового курса «Математика для Data Science» делимся с вами переводом еще одного полезного материала.
Об этой статье
Эта статья содержит лишь малую часть информации по заявленной теме. Рассматривайте ее как вводный курс перед началом всестороннего изучения предмета. Надеюсь, вы найдете в ней полезную информацию. Знание дискретной математики помогает описывать объекты и задачи в информатике, особенно когда дело касается алгоритмов, языков программирования, баз данных и криптографии. В дальнейшем я планирую подробнее раскрыть темы, затронутые в этой статье. Приятного чтения!
ЧТО ТАКОЕ ДИСКРЕТНАЯ МАТЕМАТИКА?
Это область математики, изучающая объекты, которые могут принимать только уникальные отдельные значения.
Мы рассмотрим пять основных разделов в следующем порядке.
ЛОГИКА
Что такое логика?
Это наука о корректных рассуждениях. Мы будем использовать приемы идеализации и формализации. Неформальная логика изучает использование аргументов в естественном языке.
Формальная логика анализирует выводы с чисто формальным содержанием. Примерами формальной логики являются символическая логика и силлогистическая логика (о которой писал Аристотель).
Начнем с азов. Рассмотрим следующее высказывание на естественном языке:
«Если я голоден, я ем».
Пусть «голоден» будет посылкой A, а «ем» — следствием B. Попробуем формализовать:
A => B (то есть из A следует B)
NB. Посылка и следствие являются суждениями.
Логические выражения
Для нас важна форма, а НЕ содержание. Значение будет истинным, если оно соответствует форме.
Например, 10 4 — ИСТИНА.
Логические операции
Суждение P — это утверждение, которое может быть как истинным, так и ложным.
Обозначим истинное значение P единицей (1), а ложное значение P нулем (0).
Существует другое суждение; обозначим истинное значение Q единицей (1), а ложное значение Q нулем (0).
Рассмотрим логические операции с суждениями, значение которых истинно. Они могут сами образовывать истинные значения путем выполнения соответствующих операций над истинными значениями.
Дискретные структуры: матан для айтишников
Посмотришь на любую программу обучения по IT-специальности, и тут же увидишь дисциплину «Дискретная математика» (возможно, под другим названием), обычно для перво- или второкурсников. И её наличие вполне разумно, поскольку дискретная математика и непрерывная математика (представленная на первом курсе институтов с незапамятных времён математическим анализом) — две грани единой Математики, — красивой, могучей науки.
Хотя раньше такого понятия, как «дискретная математика» вовсе не было, это не значит, что не возникало дискретных задач: Абель, Дирихле, Фибоначчи, Эйлер, чьи имена возникают по ходу изучения дискретной математики, — отнюдь не наши современники! Но просто в те времена для выделения самостоятельной ветви математики ещё не сложилось критической массы задач и приёмов, не было видно взаимосвязей между ними. А большое количество плодотворных взаимосвязей между, на первый взгляд, различными понятиями, — то, что математики в своей науке очень ценят.
Ну хорошо, математикам всё математическое интересно. А зачем дискретная математика программисту?
Зачем это айтишнику
Во-первых, многие идеи, которые особенно ярко иллюстрируются на дискретных задачах, неотъемлемы и для информатики. Взять, хотя бы, фундаментальные понятия рекурсии и индукции.
Рекурсия — это, дословно, возврат, обращение к самому себе. Хорошо известные вездесущие числа Фибоначчи проще всего определяются рекурсивно: первые два числа Фибоначчи равны единице, а каждое следующее число равно сумме двух своих предшественников: 1,1,2,3,5,8,… Таким образом, для вычисления очередного числа мы обращаемся к уже рассчитанным числам такого же вида. Трудно представить, как можно изучить функциональное программирование, да и многое из других областей информатики, не освоившись хорошо с рекурсией. Очень близкий процесс к рекурсии — это индукция, способ доказательства математических утверждений, при котором в доказательстве сложных случаев мы опираемся на более простые. Параллели с рекурсией очевидны, и действительно, обычное дело, когда индуктивное доказательство существования какого-то объекта можно переформулировать в описание рекурсивного способа построения этого объекта.
Раз речь зашла о таких фундаментальных вещах, как индукция и рекурсия, не могу не сказать, что многие приёмы, которые очень хорошо видны на примерах из дискретной математики, эффективны в математике в целом. Это не только индукция, но и принцип Дирихле, принцип выбора по среднему значению и другие.
Следующий элемент, без которого информатику нельзя представить — это графы. Простейшие алгоритмы на графах обязательно входят в любой, даже самый вводный, курс по алгоритмам. Скажем, с понятием гамильтонова цикла связана одна из классических задач информатики, задача коммивояжёра.
Ещё одно архиважное умение — считать точно и оценивать приблизительно количества. Например, как вычислить количество раз, которые выполняется операция сравнения в цикле:
Или вот ещё пример. Нужно из списка из 100 товаров выбрать 20, так, чтобы их суммарная стоимость была ровно 2000 рублей («без сдачи»). Это вариант классической задачи о рюкзаке. Допустим, ваш коллега, подумав ночь, предложил решать задачу перебором: перебрать всевозможные наборы из двадцати товаров, и, как только в ходе перебора возникнет нужный набор, выдать его в качестве ответа. Между прочим, характеристика «переборный» далеко не всегда ставит клеймо на алгоритме. Всё зависит от размера входных данных. Так вот, как прикинуть, удастся ли за разумное время решить перебором эту задачу выбора 20 объектов из 100?
Наконец, для современного «дизайнера алгоритмов» обязателен к пониманию и вероятностный метод. Это общий метод, позволяющей решать многие задачи в современной комбинаторике. Очень часто наилучшие решения задач, известные на сегодняшний день, получены именно этим методом. Для практика же овладение этим методом полезно постольку, поскольку вероятностные алгоритмы прочно заняли место в современной информатике. И при анализе работы таких алгоритмов очень помогает интуиция, развитая в ходе изучения вероятностного метода.
Онлайн-курс «Дискретные структуры»
С верой в то, что перечисленные понятия из дискретной математики действительно не помешают любому программисту, а, скорее, помешает их незнание, я читаю соответствующий курс на факультете ФИВТ МФТИ. А недавно у меня появилась возможность сделать онлайн-курс, чем я с радостью воспользовался. Записаться на него можно по ссылке. Главное, чего я пожелаю всем записавшимся: не побоявшись трудностей, пройти курс до самого конца, и получить заслуженное звание Дипломированного Дискретчика. В общем, чтобы MOOC прошёл без мук и обогатил знаниями! Да и собственная корысть у меня тут тоже есть: чем больше онлайн-учеников у меня будет, тем большему я смогу научиться, читая обсуждения и наблюдая статистику решения задач. Ведь учиться учить тоже никогда не поздно!
Какие знания потребуются
Для прохождения первых двух модулей потребуются только школьные знания. Третий модуль потребует знание основ математического анализа на уровне «что такое предел» и «какая из функций x 20 или 2 x растёт быстрее (чему равны производные функций)». Для последних трёх модулей понадобится представление о том, что такое вероятность, условная вероятность, математическое ожидание, дисперсия. Также хорошо бы знать, что такое базис и размерность линейного пространства. Если с вероятностью и линейной алгеброй вы не знакомы, можно записаться заодно на эти вводные курсы. Тогда как раз, к моменту, когда нам потребуются эти знания, они у вас будут.
Post scriptum
Меня можно было бы упрекнуть в конфликте интересов, всё-таки я математик, и, естественно, хочу приобщить к своей секте как можно больше завсегдатаев Хабра. В своё оправдание могу сослаться на этот ответ на Quora. Под большей частью тем, перечисленных в этом ответе, я готов лично подписаться, в онлайн-курс многие из них вошли. Ещё сошлюсь на подборку мнений яндексоидов.
👨🎓️ Нужны ли программисту математика, английский язык, теория алгоритмов и паттерны проектирования?
Ilya Ginsburg
Иногда возникают нюансы. Вам приходится не только писать код, но и формализовать задачу, поставленную заказчиком на манер знаменитого «копать от забора и до обеда». Или ваш код, написанный «на коленке» за пару минут, работает слишком медленно. Или ваша программа выдает исключение, давно описанное на stackoverflow.com, но вы не умеете читать по-английски. Или возникает необходимость сделать рефакторинг кода, а для вас это звучит как «харакири». Как правило, начальству наплевать на то, как вы справитесь с этими проблемами, но справиться вы обязаны – «вы же программист»! За что же вам платят эдакие деньжищи?
Математика
Давным-давно, когда компьютеры были большими, а зарплаты программистов – маленькими, каждый программист был математиком. Помните главного героя «Понедельника начинается в субботу» братьев Стругацких, программиста Сашу Привалова?
— Кристобаль Хозевич, – сказал я. – Я ее все-таки решил. Вы были совершенно правы. Пространство заклинаний действительно можно свернуть по любым четырем переменным…
…Я отдал ему листки, он сел рядом со мною, и мы вместе разобрали задачу с начала и до конца и с наслаждением просмаковали два изящнейших преобразования, одно из которых подсказал мне он, а другое нашел я сам…
– Это мы опубликуем. Это никому не стыдно опубликовать.
Аркадий и Борис Стругацкие, «Понедельник начинается в субботу»
На минуточку: обычный программист (пусть даже заведующий вычислительным центром) знал математику настолько хорошо, чтобы придумать в ней что-то новое, достойное публикации! То есть, фактически был профессиональным математиком. А как же еще? В те времена считалось, что программист должен уметь самостоятельно формализовать задачу, и только потом написать программу для ее решения.
В моем дипломе, полученном на факультете прикладной математики, гордо значится специальность – математик. Хотя все понимали, что нас учат на программистов. Нас научили использовать численные методы для решения сложных задач, которые нельзя решить аналитически – например, уравнения теплопроводности. Пригодилось ли это на практике? Пока нет, но еще может пригодиться. Если говорить о нужности для программиста, всю высшую математику можно разделить на три части:
Дискретная математика
Этот раздел математики изучает конечные структуры и содержит множество различных подразделов. Самый важный подраздел для программистов – это математическая логика, в которую входит обработка привычных каждому программисту логических операций вроде and, or, и not. Например, следующий оператор срабатывает, если верно a, но не b, или, наоборот, верно b, но не a:
Если вы изучали дискретную математику, то сразу поймете, что то же самое можно написать гораздо проще, используя операцию «исключающее ИЛИ», причем код будет не только намного короче, но и станет работать быстрее:
Математическая логика также помогает «инвертировать» логические выражения или упрощать их, что может потребоваться программисту буквально каждый день:
Еще один важнейший раздел дискретной математики для программистов – это теория графов. Если слово «граф» для вас ассоциируется с графом Монте-Кристо, а не со структурой данных, состоящей из вершин и соединяющих их ребер, вы рискуете не только провалиться на любом собеседовании, но еще и опозориться:
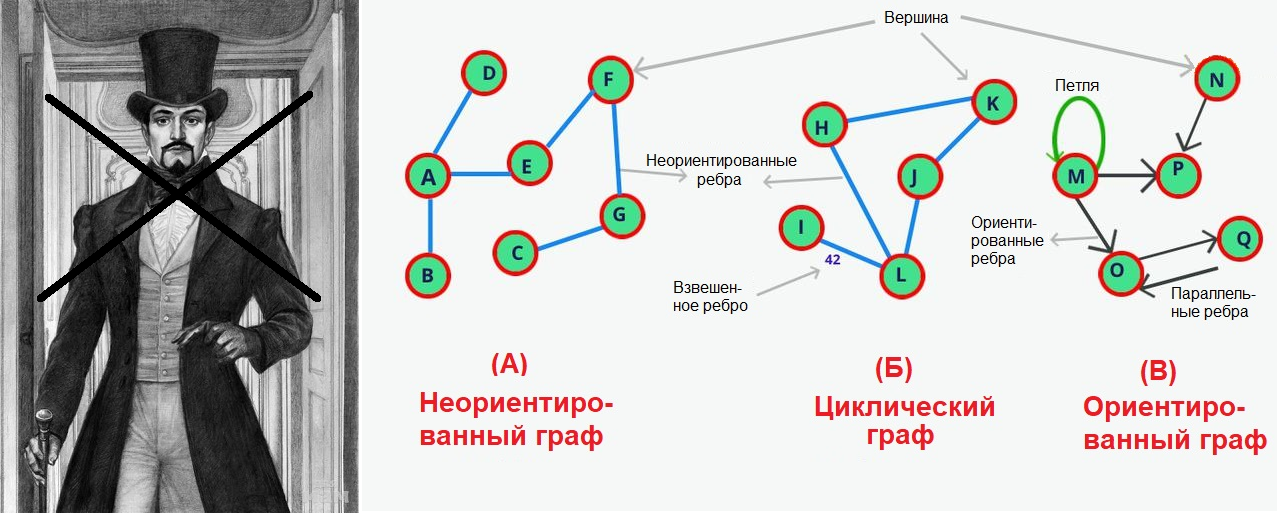
Теория графов имеет огромное значение для программистов, поскольку большинство реально встречающихся на практике сложных задач описываются в терминах графов, и именно в этих терминах описываются алгоритмы решения таких задач. Очень популярным подвидом графа является дерево – это связный граф без циклов. Полное незнание теории графов не позволит вам найти нужные алгоритмы и тем более понять их.
Алгоритмы на графах очень часто применяются в реальной жизни. Моей первой реальной задачей была визуализация проектных связей изделия, и схема этих проектных связей, разумеется, была графом. Эта задача до сих пор актуальна и популярна.
Английский язык
Если вы не умеете быстро и без напряжения читать книги по программированию на английском языке – это значит, что вы просто не сможете постоянно следить за передним краем даже в своей области, не говоря уже о смежных. Конечно, российские издательства выпускают переводы книг по программированию, но к моменту их выхода на Западе уже успевает выйти новое издание. К тому же качество этих переводов настолько плохое, что я предпочитаю читать книги в оригинале, то есть на английском. Зачастую электронные версии самых свежих книг на английском языке появляются задолго до их печати, то есть я могу осваивать новые технологии одновременно со всем миром. К тому же, книг по программированию выходит так много, что далеко не каждая из них вообще будет переведена на русский!
Иногда вам придется и написать абзац-другой – например, задать вопрос на форуме или в отдел технической поддержки. Поскольку писать сочинения вроде «London is the capital of Great Britain» вам едва ли понадобится, это не должно вызвать особых трудностей, если вы уже хорошо умеете читать. Даже если вы сделаете пару ошибок, не страшно – лишь бы вас правильно поняли.
Многие фирмы работают на Запад, и там регулярно проводятся совещания на английском языке. Вот там вам уже понадобятся и разговорные навыки, и аудирование, и даже хорошее произношение. Такие фирмы прямо пишут в своих вакансиях что-то вроде «English – Upper-Intermediate». Высококлассному специалисту с большим опытом должно быть очень обидно упускать такие вакансии только из-за незнания языка.
С другой стороны, многие фирмы устраивают своим сотрудникам бесплатные курсы английского языка. Не упускайте эту возможность! Знание языка – это не излишество, а необходимость. Несмотря на то, что сам код можно писать, не зная даже английского алфавита.
Теория алгоритмов
Теория алгоритмов оценивает не точное количество ресурсов (которое на практике редко можно рассчитать), а характер его зависимости от размеров исходных данных, называемой сложностью. Например, цикл по всем элементам массива имеет вычислительную сложность O(N), где N – количество элементов массива. Это значит, что количество вычислительных операций пропорционально N. Общеизвестно, что сложность быстрой сортировки (в среднем) равна O(N * logN), а сложность бинарного поиска – O(log N). Поиск в хеш-таблице происходит еще быстрее: при правильно подобранных ключах и достаточном размере таблицы его сложность O(1), то есть вообще не зависит от размера входных данных! Этим и обусловлена широкая популярность хеш-таблиц, а также базирующихся на них словарей (dictionary) и множеств (set).
Использование неоптимального алгоритма – это мина замедленного действия, заложенная под ваш продукт. Предположим, что вы взяли на работу новичка, не знающего, что такое бинарный поиск. Как, по-вашему, он будет искать нужный элемент в массиве? Правильно, перебором всего массива – то есть операция, которая даже для миллионов элементов должна занимать несколько секунд, у него займет несколько дней, недель или даже месяцев. Именно поэтому тимлид должен отлично разбираться в теории алгоритмов, чтобы не брать на работу тех, кто не знает даже ее основ, а также помогать своей команде искать и придумывать лучшие алгоритмы.
Теоретически, вы можете писать код, и не зная об алгоритмах, но это будет код школьника-троечника. Причем страшнее всего то, что вы этого даже не почувствуете! Если вам не хватает английского языка – это всегда очевидно: вы не можете понять текст, постоянно лезете в словарь, или, что еще хуже, пользуетесь автоматическим переводчиком. Если вам не хватает математической подготовки – вы, конечно, не сможете обнаружить нехватку самостоятельно, но хотя бы почувствуете, что чего-то не понимаете. А вот люди, ничего не знающие об алгоритмах, не получают никаких «звоночков». Они успешно пишут код, который прекрасно проходит все тесты (поскольку размер данных в тестах обычно невелик), но у пользователя работать не будет.
Поэтому теория алгоритмов программисту действительно необходима, она применяется практически каждый день. При этом не обязательно уметь придумывать новые алгоритмы самостоятельно, но оценивать сложность своих алгоритмов и искать более эффективные алгоритмы для ваших задач точно нужно уметь.
Паттерны проектирования
Пожалуй, впервые важность проектирования была продемонстрирована в книге Ф.Брукса «Мифический человеко-месяц», вышедшей в далеком 1975-м, но она была ориентирована на менеджеров, а не на программистов. В 1994-м Э. Гамма, Р. Хелм, Р. Джонсон и Д. Влиссидес (называемые «бандой четырех», «Gang of Four») опубликовали книгу «Паттерны объектно-ориентированного проектирования», заложившую основы современного подхода к проектированию ПО. В книге описано множество типовых приемов (которые авторы назвали «паттернами»), помогающих улучшить проекты проекты программ, и это стало основным фактором ее популярности. Стало модно задавать вопросы по паттернам проектирования на собеседованиях, и юные соискатели начали заучивать их наизусть. (Я не рассматриваю SOLID, появившийся позднее, поскольку он слабо помогает проектировать – но заучить его для собеседований вам тоже придется).
К сожалению, навыки кодирования и проектирования очень сильно отличаются друг от друга, так что гениальный проектировщик вряд ли окажется еще и супер-кодировщиком (а когда такое все же случается, в мире появляется очередной Линус Торвальдс). Типичный кодировщик – это юноша, очень быстро набирающий код, то есть обдумывающий его еще быстрее. Типичный проектировщик – это человек с большим опытом, который может не набрать ни одной строки кода на протяжении нескольких дней или даже недель. Его задача – придумать наилучшую архитектуру продукта, вот он и думает. Разумеется, кодировщики, ничего не знающие о проектировании, считают проектировщика просто бездельником! Именно поэтому крупные компании не ставят проектировщика в подчинение руководителю команды кодировщиков, а придумывают для него особую должность «архитектора» (software architect).
Отличный пример широко распространенного, но неправильного понимания паттерна проектирования дает паттерн Bridge (Мост). Начнем с правильного примера использования этого паттерна на C# (код взят из документации Microsoft):
Интерфейс IDBConnection реализует Мост между клиентским приложением и базой данных (БД). Цель паттерна – полная изоляция клиента от деталей реализации каждой конкретной БД. Конкретным объектом, реализующим этот интерфейс, может быть любой экземпляр класса, унаследованного от DBConnection (код создает экземпляры SqlConnection, OdbcConnection и OleDbConnection), но клиент никогда не должен узнать, какого именно. Это позволяет разработчикам клиентского приложения сделать его по-настоящему мультиплатформным, а разработчикам Моста – постепенно добавлять поддержку новых БД, которая не заставит разработчиков клиента ничего менять. Важная парадигма: для клиентского приложения оба «берега», соединяемых Мостом, всегда представляют одно и то же (в нашем примере – БД), только на «его» берегу находится абстрактное представление о БД, а на «чужом» – ее конкретная реализация.
Теперь взгляните, какой «пример Моста» приведен на сайте Метанит. Там объект программиста обращается к объекту языка программирования через «мост». Непонятно, зачем изолировать объекты языков программирования от объектов программистов, но проблема даже не в этом. Во-первых, вы не можете заранее предсказать все, что вам потребуется от языков программирования – а это значит, что ваш «мост», скорее всего, через некоторое время придется изменять, тогда как одна из целей настоящего Моста заключается именно в защите клиента от изменений (как вы думаете, будет ли когда-нибудь изменен IDBConnection?). Во-вторых, вы не можете раз и навсегда определить даже вид соотношения между языками и программистами! Кто сказал, что каждый программист знает только один язык? Такие «мосты» только напрасно усложняют проект и не приносят никакой реальной пользы.
А вот пример того же паттерна с сайта Refactoring Guru. Здесь строится «мост» между пультами и управляемыми с их помощью устройствами. Этот пример уже имеет смысл, поскольку управлять с пульта проще, чем кнопками на устройстве (клиенту всегда проще работать с абстрактным интерфейсом Моста, избавляющим его от ненужных деталей реализации), но все-таки он неудачен. Не все команды управления телевизором и радио будут совпадать. Но самое главное – пульт не скрывает от клиента конкретную реализацию: клиент по-прежнему смотрит телевизор, а не пульт, и слушает радио, а не пульт. А мы уже знаем, что основная цель Моста – именно изоляция клиента от конкретной реализации.
Удачи вам в определении того, чего вам не хватает, и успешного устранения этих пробелов!