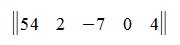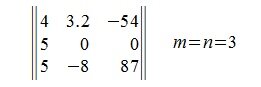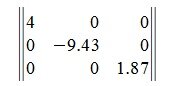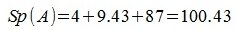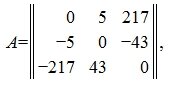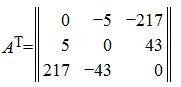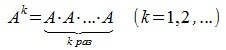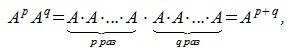Для чего нужна единичная матрица

Единичная матрица

Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Содержание

Определение

Квадратная матрица размера (порядка ), где для всякого , и для всяких , называется единичной матрицей порядка .

Единичную матрицу можно определить как матрицу , у которой , где — символ Кронекера.

Единичная матрица является частным случаем скалярной матрицы.

Обозначение

Единичная матрица размера обычно обозначается и имеет вид:

Так же используется и другое обозначение: .

Если из контекста ясно, какого размера матрица, то нижний индекс (указывающий порядок) опускается: , .

Свойства

Примеры

Единичные матрицы первых порядков имеют вид

Замечание

Если взять две матрицы —: матрицу и единичную — то, приведением матрицы к единичной методом Гаусса, можно добиться одновременного приведения матрицы к матрице .

Литература

См. также

Полезное

Смотреть что такое «Единичная матрица» в других словарях:

единичная матрица — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] единичная матрица Такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу — единицы, а остальные… … Справочник технического переводчика

Единичная матрица — [unit matrix, identity matrix] такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу единицы, а остальные нули, например: Е.м. применяется в процессе обращения матриц, в … Экономико-математический словарь

единичная матрица — vienetinė matrica statusas T sritis fizika atitikmenys: angl. identity matrix; unit matrix vok. Einheitsmatrix, f rus. единичная матрица, f pranc. matrice unité, f; matrice unitaire, f … Fizikos terminų žodynas

Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь

матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика

МАТРИЦА ПЛОТНОСТИ — (статистический оператор), оператор, при помощи к рого можно вычислить ср. значение любой физ. величины в квант. статистич. механике и, в частном случае, в квант. механике. Термин «М. п.» связан с тем, что статистич. оператор задаётся обычно в… … Физическая энциклопедия

Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия

Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия

Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия

Матрица Адамара — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Матрица … Википедия

Источник

От действий над матрицами к пониманию их сути…

Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.

Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.

Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.

Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.

Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.

Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…

Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.

Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?

Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…

Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.

В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.

Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».

Источник

Единичная матрица

Содержание:

Диагональная матрица, все диагональные элементы которой равны единице , называется единичной матрицей и обозначается символом .

Элементы единичной матрицы могут быть представлены с помощью дельта-символа Кронекера:

(2)

Единичная матрица представляет собой квадратную матрицу, элементы которой находятся на главной диагонали, а остальные элементы равны нулю. Обозначается символом Е.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Согласно определению матричного произведения и с учетом свойств дельта-символа,

(3)

для любых допустимых значений индексов , следовательно, АЕ = А.

Умножение матрицы на единичную матрицу дает ту же матрицу.

Примеры с решением

Пример 1

диагональная матрица второго порядка,

диагональная матрица третьего порядка.

Определение Если у диагональной матрицы -го порядка Е все диагональные элементы равны единице, то такая матрица называется единичной матрицей -го порядка.

Возможно вам будут полезны данные страницы:

Пример 2

— единичная матрица третьего порядка.

Определение Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю: В отличие от чисел, где число 0 единственно, нулевых матриц бесконечно много, т. к. каждому размеру матриц соответствует нулевая матрица этого размера.

Нетрудно убедиться, что при умножении единичная матрица играет ту же роль, что и число 1 при умножении чисел: единичная матрица -го порядка перестановочна с любой квадратной матрицей А того же порядка, причем

Чтобы доказать это, введем обозначения: АЕ = F, ЕА = G. Используя правило умножения матриц и определение единичной матрицы

(2.13)

находим, что для всех

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Для чего нужна единичная матрица

Трудно представить себе систему чисел, которая бы не содержала единичный элемент. В частности, именно единица является результатом умножения числа a на ему обратное. Алгебра любых объектов (вещественных или комплексных чисел, векторов и так далее) должна включать в себя единичный элемент. Не является исключением и матричная алгебра, в которой роль единицы играет диагональная матрица, все диагональные элементы которой равны единице.

В качестве определения единичной матрицы могло бы выступать примерно такое.

Матрица E называется единичной, если при умножении на нее любой матрицы A (слева и справа) матрица A остается неизменной: AE = EA = A.

Связано это с тем, что операция умножения определена не для любых матриц и, следовательно, требуется определенное согласование размеров иатриц-сомножителей. В результате под единичной матрицей понимается матрица вышеуказанной структуры, порядок которой выбирается таким, чтобы соответствующее произведение было определено.

Диагональная матрица, все диагональные элементы которой равны единице (), называется единичной матрицей и обозначается символом E.
Элементы единичной матрицы могут быть представлены с помощью дельта-символа Кронекера:

.

(1)

В матричной алгебре матрица E играет ту же роль, что число единица в системе вещественных чисел, а именно – при умножении на единичную матрицу (справа или слева) исходная матрица не изменяется:

Рассмотрим теперь i,j-ый элемент матричного произведения EA, где E – единичная матрица m-го порядка:

Источник

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Матрица столбец

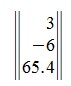
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

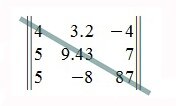
Главная диагональ матрицы

Побочная диагональ матрицы

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

След матрицы

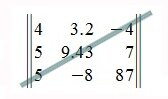
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

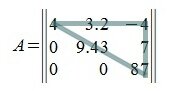
Верхняя треугольная матрица

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

где E-единичная матрица.

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Источник