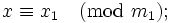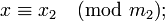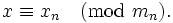Для чего нужна факториальная система счисления
Нетрадиционные системы счисления
Читателям газеты-вкладки “В мир информатики” конечно же известно, что существуют два вида систем счисления: позиционные и непозиционные. А знаете ли вы, что позиционные системы, в свою очередь, можно разделить на традиционные и нетрадиционные?
Напомним основные положения. В позиционной системе счисления количественный эквивалент цифры зависит от ее положения в записи числа. Для таких систем мы фиксируем некоторое основание — целое положительное число
р 
Аналогично и для чисел, записанных в других системах счисления:
10001102 = 1 · 2 6 + 0 · 2 5 + 0 · 2 4 + 0 · 2 3 + 1 · 2 2 + 1 · 2 1 + 0 · 2 0 ;
Последовательность чисел, каждое из которых задает “вес” соответствующих разрядов, и называют базисом системы счисления. Из приведенных примеров видно, что базисы десятичной, двоичной, шестнадцатеричной систем счисления образуют геометрическую прогрессию со знаменателем р, равным 10, 2 и 16 соответственно.
Позиционные системы счисления, в которых цифры являются неотрицательными числами, а базис образуют члены геометрической прогрессии, называют классическими, или традиционными [1].
Если какое-то из перечисленных условий не соблюдается, то речь идет о нетрадиционной системе счисления. В статьях [2–3] рассказывалось, например, о троичной уравновешенной системе счисления с цифрами –1, 0 и 1 (присутствует отрицательное число). А можно ли в качестве базиса выбрать не геометрическую прогрессию, а некоторую последовательность натуральных чисел? Оказывается, да. Такая система, например, применялась для календаря и астрономических наблюдений индейцами племени майя. Они использовали 20-ричную систему счисления за некоторым исключением: р0 = 1, р1 = 20, р2 = 18, р3 = 20, р4 = 20 и т.д. Это было сделано для облегчения расчетов календарного цикла. Например, число 100 в этой системе, равное 1 · 18 · 20 + 0 · 20 + 0 · 1 = 360, есть примерно число дней в нашем, “солнечном”, году. У индейцев 20 дней-кинов образовывали месяц (виналь, или уинал), 18 месяцев-уиналов образовывали год (тун) и так далее:
Виналь = 20 кин = 20 дней.
Тун = 18 виналь = 360 дней = около 1 года.
Катун = 20 тун = 7200 дней = около 20 лет.
Бактун = 20 катун = 144 000 дней = около 400 лет.
Пиктун = 20 бактун = 2 880 000 дней = около 8000 лет.
Калабтун = 20 пиктун = 57 600 000 дней = около 160 000 лет.
Кинчильтун = 20 калабтун = 1?152?000?000 дней =
= около 3 200 000 лет.
Алавтун = 20 кинчильтун = 23 040 000 000 дней =
= около 64 000 000 лет.
Также в качестве примера можно рассмотреть представление времени в виде количества суток, часов, минут и секунд. При этом величина “d дней h часов m минут s секунд” соответствует значению d · 24 · 60 · 60 + + h · 60 · 60 +
+ m · 60 + s секунд.
Рассмотрим еще две нетрадиционные системы счисления.

— где dk — цифра числа (0 

+ 2 · 2! + 0 · 1! = 243220f (буква f в виде индекса говорит о записи числа в факториальной системе).
Фибоначчиева система счисления известна еще более узкому кругу специалистов. Из названия нетрудно догадаться, что она основывается на числах Фибоначчи. В этой системе счисления вес k-го разряда равен k-му числу Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55, … (каждый член, начиная с третьего, равен сумме двух предыдущих). Используемые цифры (алфавит) — только 0 и 1. Следовательно, если запись числа в фибоначчиевой системе имеет вид fn fn–1…f2f1, то этому числу соответствует десятичное значение, равное 
Необходимо отметить, что, хотя для записи числа в этой системе счисления используются только цифры 0 и 1, эту запись нельзя считать двоичным представлением числа.
Задания для самостоятельной работы 2
1. Какие из чисел записаны не по правилам факториальной системы счисления: 42220, 44000, 86633300, 8663320?
2. Определите десятичный эквивалент чисел, записанных
а) в факториальной системе: 502101, 4422310;
б) в фибоначчиевой системе: 10010101, 101010101.
3. Запишите десятичные числа 34502 и 45087012 в факториальной системе счисления.
4. Перечислите первые 14 натуральных чисел в фибоначчиевой системе счисления. Проанализируйте полученные числа и сформулируйте правила перечисления натуральных чисел (правила получения очередного числа) в этой системе.
5. Запишите десятичные числа 30, 125 и 1949 в фибоначчиевой системе счисления.
6. Объясните, какое отношение имеют необычные счеты, показанные на рисунке, к данной статье? Какое десятичное число отложено на правых счетах?
7. На известном вам языке программирования напишите программы перевода десятичного натурального числа N (N 
В заключение ответим на вопрос, который скорее всего возник у читателей: а зачем нужны такие системы счисления? Факториальная система счисления используется, например, специалистами в теории чисел для нумерации перестановок. Системы, аналогичные фибоначчиевой, применяются при кодировании информации. В свое время была даже сделана попытка создания компьютера, основанного на фибоначчиевой системе счисления [1]. Это теоретически и практически интересные системы записи чисел. Изучение особенностей таких систем продолжается и в настоящее время, и у наших читателей есть возможность заняться серьезным исследованием данного вопроса.
1. Андреева Е.В., Босова Л.Л., Фалина И.Н. Математические основы информатики. Элективный курс: Учебное пособие. М.: БИНОМ. Лаборатория знаний, 2005.
2. О троичной системе счисления. / Информатика, № 4/2006.
3. Гашков С.Б. Системы счисления и их применения. / Информатика, № 4/2006.
4. Кузьмищев В.А. Тайна жрецов майя. М.: Молодая гвардия, 1975.
5. Касаткин В.Н. Новое о системах счисления. Киев: Выща школа, 1982.
1 Имеется также вариант фибоначчиевой системы счисления, в которой в записи чисел не допускаются два рядом стоящих нуля. — Прим. ред.
2 Ответы и/или программы (можно не все) присылайте в редакцию. Фамилии всех приславших будут опубликованы, а лучшие ответы мы поощрим. — Ред.
Факториальная система счисления
В факториальной системе счисления основаниями являются последовательность факториалов 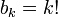

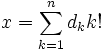
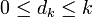
Факториальная система счисления используется при декодировании перестановок списками инверсий: имея номер перестановки, можно воспроизвести её саму следующим образом: число, на единицу меньшее номера (нумерация начинается с нуля) записывается в факториальной системе счисления, при этом коэффициент при числе i! будет обозначать число инверсий для элемента i+1 в том множестве, в котором производятся перестановки (число элементов меньших i+1, но стоящих правее его в искомой перестановке)
Фибоначчиева система счисления
Основная статья: Фибоначчиева система счисления
Фибоначчиева система счисления основывается на числах Фибоначчи. Каждое натуральное число 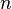
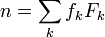
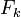
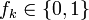
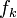
Непозиционные системы счисления
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания.
Биномиальная система счисления
Представление, использующее биномиальные коэффициенты
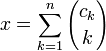
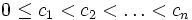
Система остаточных классов (СОК)
Представление числа в системе остаточных классов основано на понятии вычета и китайской теореме об остатках. СОК определяется набором взаимно простых модулей 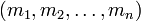
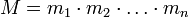

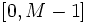
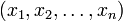
При этом китайская теорема об остатках гарантирует однозначность представления для чисел из отрезка 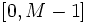
В СОК арифметические операции (сложение, вычитание, умножение, деление) выполняются покомпонентно, если про результат известно, что он является целочисленным и также лежит в 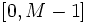
Недостатками СОК является возможность представления только ограниченного количества чисел, а также отсутствие эффективных алгоритмов для сравнения чисел, представленых в СОК. Сравнение обычно осуществляется через перевод аргументов из СОК в смешанную систему счисления по основаниям 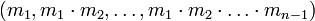
Дата добавления: 2018-05-12 ; просмотров: 3148 ; Мы поможем в написании вашей работы!
Факторная система счисления
Содержание
Определение [ править ]
| Radix | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Место значение | 7! | 6! | 5! | 4! | 3! | 2! | 1! | 0! |
| Поместите значение в десятичную дробь | 5040 | 720 | 120 | 24 | 6 | 2 | 1 | 1 |
| Максимально допустимая цифра | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Например, 463 10 можно преобразовать в факторное представление следующими последовательными делениями:
| 463 ÷ 1 = 463, остаток 0 463 ÷ 2 = 231, остаток 1 231 ÷ 3 = 77, остаток 0 77 ÷ 4 = 19, остаток 1 19 ÷ 5 = 3, остаток 4 3 ÷ 6 = 0, остаток 3 |
Примеры [ править ]
При сортировке по столбцу, в котором справа пропущен 0, факториальные числа в этом столбце соответствуют номерам индексов в неподвижном столбце слева. Маленькие столбцы являются отражением соседних столбцов, и их можно использовать для приведения их в колексикографический порядок. В крайнем правом столбце показаны суммы цифр факториалов ( OEIS : A034968 в порядке по умолчанию в таблицах).
В другом примере, наибольшее число, которое может быть представлено шестью цифрами, будет 543210 ! что равно 719 в десятичной системе :
Факториальная система счисления обеспечивает уникальное представление каждого натурального числа с заданным ограничением используемых «цифр». Ни одно число не может быть представлено более чем одним способом, потому что сумма последовательных факториалов, умноженная на их индекс, всегда равна следующему факториалу за вычетом единицы:
Перестановки [ править ]
| десятичный | факторский | перестановка |
|---|---|---|
| 0 10 | 0: 0: 0 ! | (0,1,2) |
| 1 10 | 0: 1: 0 ! | (0,2,1) |
| 2 10 | 1: 0: 0 ! | (1,0,2) |
| 3 10 | 1: 1: 0 ! | (1,2,0) |
| 4 10 | 2: 0: 0 ! | (2,0,1) |
| 5 10 | 2: 1: 0 ! | (2,1,0) |
В каждом случае вычисление перестановки происходит с использованием крайней левой факторадической цифры (здесь 0, 1 или 2) в качестве первой цифры перестановки, а затем удаления ее из списка вариантов (0, 1 и 2). Думайте об этом новом списке вариантов как об индексированном нулем и используйте каждую последующую фактическую цифру для выбора из оставшихся элементов. Если вторая фактическая цифра равна «0», то первый элемент списка выбирается для второй цифры перестановки и затем удаляется из списка. Точно так же, если вторая фактурная цифра равна «1», вторая выбирается и затем удаляется. Последняя фактическая цифра всегда равна «0», и поскольку список теперь содержит только один элемент, он выбирается как последняя цифра перестановки.
Процесс может стать понятнее на более длинном примере. Допустим, нам нужна 2982-я перестановка чисел от 0 до 6. Число 2982 равно 4: 0: 4: 1: 0: 0: 0 ! Фактически радикально, и это число выбирает цифры (4,0,6,2,1,3,5) по очереди, индексируя убывающий упорядоченный набор цифр и выбирая каждую цифру из набора на каждом шагу:
Естественным индексом для группового прямого произведения двух групп перестановок является конкатенация двух факторадических чисел с двумя нижними индексами «!» S.
Дробные значения [ править ]
При использовании этого метода все рациональные числа имеют завершающее раскрытие, длина которого в «цифрах» меньше или равна знаменателю представленного рационального числа. Это может быть доказано, если учесть, что существует факториал для любого целого числа, и поэтому знаменатель делится на собственный факториал, даже если он не делится на какой-либо меньший факториал.
В следующем наборе примеров пробелы используются для разделения значений разряда, иначе они представлены в десятичном виде. Рациональные числа слева также в десятичном формате:
Есть также небольшое количество констант, которые имеют шаблонное представление с помощью этого метода:
Для чего нужна факториальная система счисления
В рассмотренных выше системах счисления «вес» единицы любого разряда, кроме первого, всегда равнялся»весу» единицы предшествующего разряда, умноженному на постоянное основание системы Р. Можно, однако, привести пример такой системы счисления, в которой смысл понятия «основание системы счисления» заметно отличается от традиционного. Предлагаемая система является следствием расширения нашего представления о роли основания системы счисления. Сущность нового подхода легко представить, если рассмотреть счеты необычной конструкции.
Поскольку каждая косточка на второй проволоке заменяет две косточки, расположенные на первой проволоке, то вес этой косточки равен 2. Каждая косточка третьей проволоки заменяет три косточки второй проволоки, и, следовательно, ее вес в 6 = 3·2·1 раз больше веса косточки на первой проволоке. Из этих разъяснений следует, что косточка, расположенная на n-ой проволоке, имеет вес n!. Вес единиц от разряда к разряду растет, но неравномерно. Это приводит к представлению числа в следующем виде:
Получаем, что N-разрядное число, «списанное со счет», оказывается представленным не в виде суммы степеней основания Р, а в виде суммы факториалов n первых натуральных чисел.
Эту систему счисления относят к нетрадиционным позиционным и называют факториальной системой счисления.
С числами этой системы можно выполнять арифметические действия по правилам, незначительно отличающимся от правил десятичной арифметики.
Как и в других системах счисления, в факториальной системе можно рассматривать дробные числа.
Каких-либо существенных практических применений этой системы, основанных на необычной сущности цифрового и многочленного представления, по-видимому, нет. Рассмотрение этой системы прежде всего полезно как методический подход в расширении представлений о системах счисления и обобщении принципа позиционности.
К нетрадиционным системам счисления относят и фибоначчиеву систему счисления.
Алфавитом этой системы счисления являются цифры 0 и 1. В записи числа в фибоначчиевой системе не могут стоять две единицы подряд.
Заметим, что системы, аналогичные фибоначчиевой, применяются при кодировании чисел. Это практически и теоретически интересные системы записи чисел. Изучение особенностей таких систем продолжается и в настоящее время.
СОДЕРЖАНИЕ
Определение
| Radix | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| Место значение | 7! | 6! | 5! | 4! | 3! | 2! | 1! | 0! |
| Поместите значение в десятичную дробь | 5040 | 720 | 120 | 24 | 6 | 2 | 1 | 1 |
| Наивысшая допустимая цифра | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Например, 463 10 можно преобразовать в факторное представление следующими последовательными делениями:
| 463 ÷ 1 = 463, остаток 0 463 ÷ 2 = 231, остаток 1 231 ÷ 3 = 77, остаток 0 77 ÷ 4 = 19, остаток 1 19 ÷ 5 = 3, остаток 4 3 ÷ 6 = 0, остаток 3 |
Примеры
При сортировке по столбцу, в котором справа пропущен 0, факториальные числа в этом столбце соответствуют номерам индексов в неподвижном столбце слева. Маленькие столбцы являются отражением соседних столбцов, и их можно использовать для приведения их в колексикографическом порядке. В крайнем правом столбце показаны суммы цифр факториалов ( OEIS : A034968 в порядке по умолчанию в таблицах).
В другом примере наибольшее число, которое может быть представлено шестью цифрами, будет 543210 ! что равно 719 в десятичной системе :
Факториальная система счисления обеспечивает уникальное представление каждого натурального числа с заданным ограничением используемых «цифр». Ни одно число не может быть представлено более чем одним способом, потому что сумма последовательных факториалов, умноженная на их индекс, всегда равна следующему факториалу за вычетом единицы:
Перестановки
| десятичный | факторадический | перестановка |
|---|---|---|
| 0 10 | 0: 0: 0 ! | (0,1,2) |
| 1 10 | 0: 1: 0 ! | (0,2,1) |
| 2 10 | 1: 0: 0 ! | (1,0,2) |
| 3 10 | 1: 1: 0 ! | (1,2,0) |
| 4 10 | 2: 0: 0 ! | (2,0,1) |
| 5 10 | 2: 1: 0 ! | (2,1,0) |
В каждом случае вычисление перестановки происходит с использованием крайней левой факторадической цифры (здесь 0, 1 или 2) в качестве первой цифры перестановки, а затем ее удаления из списка вариантов (0, 1 и 2). Думайте об этом новом списке вариантов как о индексированном нулем и используйте каждую последующую факторную цифру для выбора из оставшихся элементов. Если вторая фактическая цифра равна «0», то первый элемент списка выбирается для второй цифры перестановки и затем удаляется из списка. Точно так же, если вторая фактическая цифра равна «1», вторая выбирается и затем удаляется. Последняя фактическая цифра всегда равна «0», и поскольку список теперь содержит только один элемент, он выбирается как последняя цифра перестановки.
Процесс может стать понятнее на более длинном примере. Допустим, нам нужна 2982-я перестановка чисел от 0 до 6. Число 2982 равно 4: 0: 4: 1: 0: 0: 0 ! Фактически радикально, и это число выбирает цифры (4,0,6,2,1,3,5) по очереди, индексируя убывающий упорядоченный набор цифр и выбирая каждую цифру из набора на каждом шагу:
Естественным индексом для группового прямого произведения двух групп перестановок является конкатенация двух факторадических чисел с двумя нижними индексами «!» S.
Дробные значения
При использовании этого метода все рациональные числа имеют завершающее раскрытие, длина которого в «цифрах» меньше или равна знаменателю представленного рационального числа. Это можно доказать, если учесть, что существует факториал для любого целого числа, и поэтому знаменатель делится на собственный факториал, даже если он не делится на какой-либо меньший факториал.
В следующем наборе примеров пробелы используются для разделения значений разряда, иначе они представлены в десятичном виде. Рациональные числа слева также в десятичном формате:
Есть также небольшое количество констант, которые имеют шаблонное представление с помощью этого метода: