Для чего нужна первообразная функции
Первообразная функции и общий вид
Этот урок — первый из серии видео, посвященных интегрированию. В нём мы разберём, что такое первообразная функции, а также изучим элементарные приёмы вычисления этих самых первообразных.
На самом деле здесь нет ничего сложного: по существу всё сводится к понятию производной, с которым вы уже должны знакомы.:)
Сразу отмечу, что, поскольку это самый первый урок в нашей новой теме, сегодня не будет никаких сложных вычислений и формул, но то, что мы изучим сегодня, ляжет в основу гораздо более сложных выкладок и конструкций при вычислении сложных интегралов и площадей.
Кроме того, приступая к изучению интегрирования и интегралов в частности, мы неявно предполагаем, что ученик уже, как минимум, знаком к понятиям производной и имеет хотя бы элементарные навыки их вычисления. Без четкого понимания этого, делать в интегрировании совершенно нечего.
Однако здесь же кроется одна из самых частых и коварных проблем. Дело в том, что, начиная вычислять свои первые первообразные, многие ученики путают их с производными. В результате на экзаменах и самостоятельных работах допускаются глупые и обидные ошибки.
Поэтому сейчас я не буду давать четкого определения первообразной. А взамен предлагаю вам посмотреть, как она считается на простом конкретном примере.
Что такое первообразная и как она считается
Допустим, нам необходимо посчитать следующую производную:
Мы знаем такую формулу:
Считается эта производная элементарно:
Но мы можем записать и так, согласно определению производной:
А теперь внимание: то, что мы только что записали и есть определением первообразной. Но, чтобы записать ее правильно, нужно написать следующее:
Аналогично запишем и такое выражение:
Если мы обобщим это правило, то сможем вывести такую формулу:
Теперь мы можем сформулировать четкое определение.
Первообразной функции называется такая функция, производная которой равна исходной функции.
Вопросы о первообразной функции
Казалось бы, довольно простое и понятное определение. Однако, услышав его, у внимательного ученика сразу возникнет несколько вопросов:
На последний вопрос я отвечу сразу. К сожалению, первообразная, в отличие от производной, считается не всегда. Нет такой универсальной формулы, по которой из любой исходной конструкции мы получим функцию, которая будет равна этой сходной конструкции. А что касается степеней и констант — сейчас мы об этом поговорим.
Решение задач со степенными функциями
Давайте попробуем посчитать такое выражение:
Поэтому мы с уверенностью можем записать следующее:
Эту формулу нужно знать, точно так же, как и производную степенной функции.
Итак, что нам известно на данный момент:
Идем далее. Что нам еще может потребоваться? Конечно же, правило вычисления первообразных от суммы и от разности. Запишем так:
\[f\left( x \right)\to F\left( x \right)\]
\[g\left( x \right)\to G\left( x \right)\]
\[c\cdot f\to c\cdot F\left( c=const \right)\]
А если простейшие функции мы начнем умножать и делить, как тогда посчитать первообразную произведения или частного. К сожалению, аналогии с производной произведения или частного здесь не работают. Какой-либо стандартной формулы не существует. Для некоторых случаев существуют хитрые специальные формулы — с ними мы познакомимся на будущих видеоуроках.
Однако запомните: общей формулы, аналогичной формуле для вычисления производной частного и произведения, не существует.
Решение реальных задач
Задача № 1
Давайте каждую из степенных функций посчитаем отдельно:
Возвращаясь к нашему выражению, мы запишем общую конструкцию:
Задача № 2
Как я уже говорил, первообразные произведений и частного «напролом» не считаются. Однако здесь можно поступить следующим образом:
Мы разбили дробь на сумму двух дробей.
\[F\left( x \right)=1\cdot x+\ln x\]
\[F\left( x \right)=x+\ln x\]
Все эти приемы можно и нужно комбинировать. Степенные выражения можно
Решение выражений со степенью с рациональным показателем
Пример № 1
Посчитаем каждый корень отдельно:
Итого всю нашу конструкцию можно записать следующим образом:
Пример № 2
Следовательно, мы получим:
Итого, собирая все в одно выражение, можно записать:
Пример № 3
Надеюсь, я никого не удивлю, если скажу, что то, что мы только что изучали — это лишь самые простые вычисления первообразных, самые элементарные конструкции. Давайте сейчас рассмотрим чуть более сложные примеры, в которых помимо табличных первообразных еще потребуется вспомнить школьную программу, а именно, формулы сокращенного умножения.
Решение более сложных примеров
Задача № 1
Вспомним формулу квадрата разности:
Давайте перепишем нашу функцию:
\[f\left( x \right)=\left( \sqrt[3]
Первообразную такой функции нам сейчас предстоит найти:
Собираем все в общую конструкцию:
Задача № 2
В этом случае нам нужно раскрыть куб разности. Вспомним:
С учетом этого факта можно записать так:
Давайте немного преобразуем нашу функцию:
Считаем как всегда — по каждому слагаемому отдельно:
Запишем полученную конструкцию:
Задача № 3
Сверху у нас стоит квадрат суммы, давайте его раскроем:
Давайте напишем итоговое решение:
А теперь внимание! Очень важная вещь, с которой связана львиная доля ошибок и недопониманий. Дело в том, что до сих пор считая первообразные с помощью производных, приводя преобразования, мы не задумывались о том, чему равна производная константы. А ведь производная константы равна «нулю». А это означает, что можно записать такие варианты:
Вот это очень важно понимать: если производная функции всегда одна и та же, то первообразных у одной и той же функции бесконечно много. Просто к нашим первообразным мы можем дописывать любые числа-константы и получать новые.
Еще раз переписываем наши конструкции:
Во второй нашей функции мы получим следующую конструкцию:
И вот теперь мы действительно получили то, что от нас требовалось в исходном условии задачи.
Решение задач на нахождение первообразных с заданной точкой
Сейчас, когда мы знаем о константах и об особенностях записи первообразных, вполне логично возникает следующий тип задач, когда из множества всех первообразных требуется найти одну-единственную такую, которая проходила бы через заданную точку. В чем состоит эта задача?
Дело в том, что все первообразные данной функции отличаются лишь тем, что они сдвинуты по вертикали на какое-то число. А это значит, что какую бы точку на координатной плоскости мы не взяли, обязательно пройдет одна первообразная, и, причем, только одна.
Итак, задачи, которые сейчас мы будем решать, сформулированы следующем образом: не просто найти первообразную, зная формулу исходной функции, а выбрать именно такую из них, которая проходит через заданную точку, координаты которой будут даны в условии задачи.
Пример № 1
Для начала просто посчитаем каждое слагаемое:
Теперь подставляем эти выражения в нашу конструкцию:
Давайте запишем то самое решение, которое мы искали:
Пример № 2
В первую очередь необходимо раскрыть квадрат разности по формуле сокращенного умножения:
Исходная конструкция запишется следующим образом:
Осталось отобразить итоговое выражение:
Решение тригонометрических задач
Забегая наперед, хотел бы отметить, что тот прием, который мы сейчас будем использовать для нахождения первообразных от тригонометрических функций, на самом деле, является универсальным приемом для самопроверки.
Задача № 1
Вспомним следующую формулу:
Исходя из этого, мы можем записать:
Перепишем выражение с учетом этого факта:
Задача № 2
Тут будет чуть сложнее. Сейчас увидите, почему.
Вспомним такую формулу:
Чтобы избавится от «минуса», необходимо сделать следующее:
Вот наша конструкция
Итого запишем окончательную конструкцию:
Вот и все, о чем я хотел сегодня вам рассказать. Мы изучили сам термин первообразных, как считать их от элементарных функций, а также как находить первообразную, проходящую через конкретную точку на координатной плоскости.
Надеюсь, этот урок хоть немного поможет вам разобраться в этой сложной теме. В любом случае, именно на первообразных строятся неопределенные и неопределенные интегралы, поэтому считать их совершенно необходимо. На этом у меня все. До новых встреч!
Первообразная функции
Что такое первообразная функции
Первообразная функции представляет собой такую функцию, производная которой соответствует исходной функции.
К примеру, требуется преобразовать производную, которая имеет следующий вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Известна справедливая формула:
Таким образом, можно посчитать заданную производную:
Можно выполнить следующие подробные преобразования для \(x^<2>\)
Исходя из формулировки производной, выражение можно представить и в таком виде:
Таким образом, данная запись является определением первообразной. Для корректной записи следует выполнить следующую операцию:
По аналогии можно записать следующее выражение:
При обобщении этого правила, получится формула:
Выполнив необходимые действия, можно сформулировать определение первообразной.
Основное свойство, сколько первообразных существует для функции
В том случае, когда F(х) представляет собой первообразную функцию f(х), функция F(х) + С, в которой С является произвольной постоянной, также будет первообразной функцией f(х). Таким образом, в математике все первообразные функции f(х) будут записаны в виде F(х) +С. Данное утверждение является основным свойством множества первообразных.
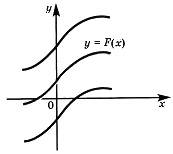
Графически все подобные первообразные данной функции f(х) получают из геометрического графика какой-то одной первообразной с помощью параллельных переносов по порядку вдоль оси Оу.
Первообразная функции и неопределенный интеграл
Неопределенным интегралом от функции f(x) называют выражение F(х)+С, то есть совокупность всех первообразных данной функции f(х).
Обозначение неопределенного интеграла:
Где f(x) представляет собой подынтегральную функцию; f(x) dx —подынтегральное выражение; x представляет собой переменную интегрирования; F(x) является одной из первообразных функции f(x); С является элементарной произвольной постоянной.
Существует несколько характерных для интеграла свойств:
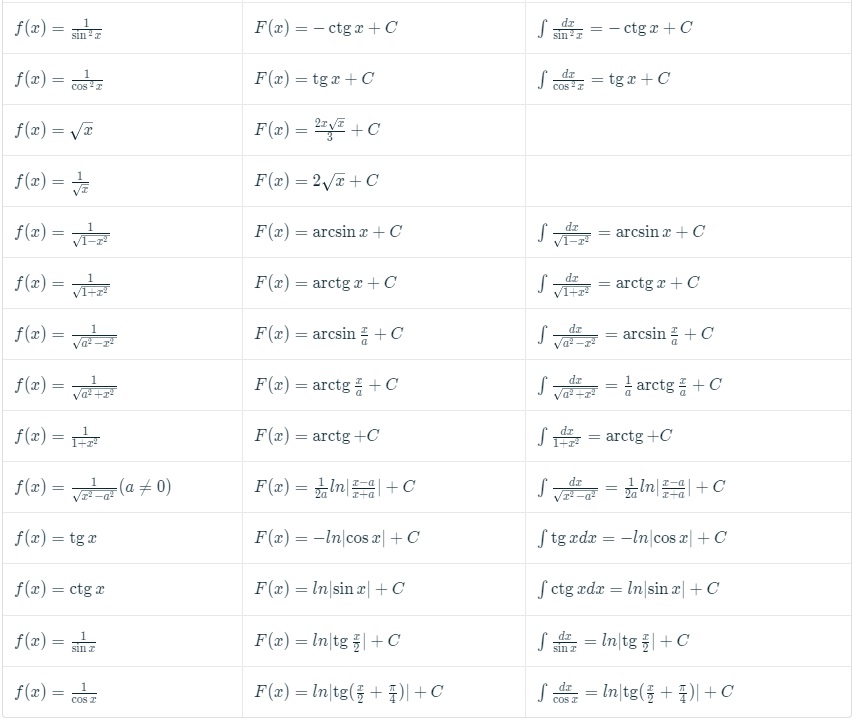
Таблица первообразных с неопределенными интегралами будет иметь следующий вид:
Допустим, что дана функция f(х), F является ее произвольной первообразной. В процессе расчетов можно записать следующее выражение для решения:
Где F(x) представляет собой первообразную для f(x).
Таким образом, интеграл функции f(х) на физическом промежутке (а;b) представляет собой разность первообразных в точках b и а.
Как записать всю совокупность первообразных функций
Элементарная запись выглядит следующим образом:
Где f (x) dx является подынтегральным выражением; f (x) представляет собой подынтегральную функцию; х — это переменная интегрирования; F (x) представляет собой первообразную для функции f (x); С — является некоторой постоянной величиной.
d является знаком дифференциала и обладает двойным назначением:
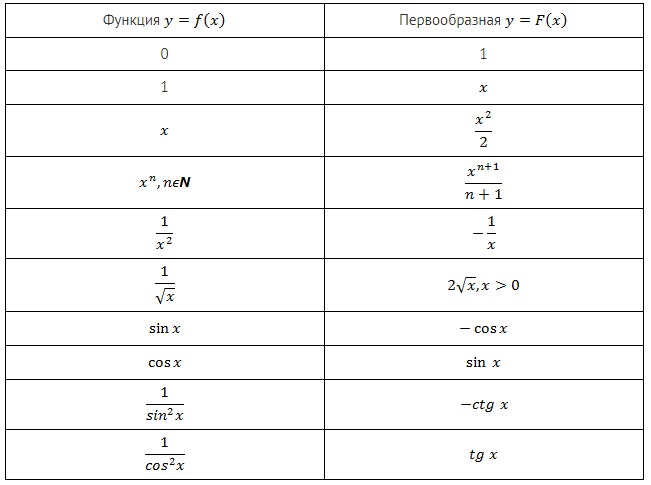
Таблица первообразных и правила их нахождения
В качестве разъяснения можно использовать пример первообразной:
Данная первообразная для функции:
В качестве подтверждения следует представить производную:
К примеру, необходимо решить пару задач:
Нахождение F(х) выполняют двумя способами:
Можно выполнить проверку:
С помощью простых вычислений можно проверить все строчки таблицы. Таким образом, будет выполняться соотношение:
С помощью специальных правил можно отыскать первообразные. Согласно первому правилу, первообразная суммы равна сумме первообразных. Допустим:
F является первообразной для f.
G является первообразной для g.
Необходимо представить доказательство выражения:
F + G является первообразной для f + g.
Второе правило о постоянном множителе. По условиям задачи:
Где F представляет собой первообразную для f; k является константой.
Требуется подтвердить, что:
kF является первообразной для kf.
Доказать данное выражение можно с помощью определения первообразной и по правилу дифференцирования. Таким образом:
Смысл правила заключается в том, что при известной первообразной для f можно получить первообразную для kf с помощью умножения F на k.
Третье правило можно записать таким образом:
если y = F(x) является первообразной для функции y = f(x),
Первообразная
Первообра́зной [1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Так, например, функция 
является первообразной 
. Так как производная константы равна нулю, 
будет иметь бесконечное количество первообразных, таких как 
или 
… и т. д. ; таким образом семейство первообразных функции 
можно обозначить как 
, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:
Если F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.
Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, 
с 
не непрерывна при 
, но имеет первообразную 
с 
.
Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:
Более развёрнутое изложение этих фактов см. в дифференциальной теории Галуа.
Содержание
Свойства первообразной
Техника интегрирования
Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого имеется несколько методов:
Другие определения
Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной 
и выполнения всюду равенства 
, иногда в определении используют обобщения производной.
Первообразная функция и неопределенный интеграл
Первообразная
Определение первообразной функции
Можно прочесть двумя способами:
Правила вычисления первообразных
Запомни!
Любая функция F(x) = х 2 + С, где С — произвольная постоянная, и только такая функция, является первообразной для функции f(x) = 2х.
Связь между графиками функции и ее первообразной:
Неопределенный интеграл
Определение:
Свойства неопределённого интеграла
Таблица первообразных и неопределенных интегралов
Функция
Первообразная
F(x) + C
Неопределенные интегралы
\int f(x) dx = F(x) + C
Формула Ньютона–Лейбница
Пусть f (х) данная функция, F её произвольная первообразная.
То есть, интеграл функции f (x) на интервале [a;b] равен разности первообразных в точках b и a.
Площадь криволинейной трапеции
Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b] функции f, осью Ox и прямыми x = a и x = b.
Площадь криволинейной трапеции находят по формуле Ньютона-Лейбница:
Первообразная
В математическом анализе первоо́бразной (первообра́зной) или примити́вной функцией данной функции f называюых; таких как (x³ / 3) + 0 или (x³ / 3) + 7 или (x³ / 3) − 36 … и т. д. ; таким образом семейство первообразных функции x² можно обозначить как F(x) = (x³ / 3) + C, где C — любое число. Графики таких первообразных смещены вертикально друг относительно друга, и их положение зависит от значения C.
Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:
Благодаря этой связи множество первообразных данной функции f иногда называют общим интегралом или неопределённым интегралом f и записывают в виде интеграла без указания пределов:
Каждая непрерывная функция f имеет первообразную F, которая представляется в виде интеграла от f с переменным верхним пределом:
функция F называется первообразной для функции f на заданном промежутке,если для всех Х из этого промежутка
Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например, f(x) = 2x sin (1/x) — cos(1/x) с f(0) = 0 не непрерывна при x = 0, но имеет первообразную F(x) = x² sin(1/x) с F(0) = 0.
Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:
Свойства первообразной
Техника интегрирования
Нахождение первообразных значительно сложнее, чем нахождение производных. Для этого в нашем распоряжении имеется несколько методов:
Другие определения
Это определение является наиболее распространенным, но встречаются и другие, в которых ослаблены требования существования всюду конечной и выполнения всюду равенства , иногда в определении используют обобщения производной.