Для чего нужна рекурсия
Простыми словами о рекурсии
В программировании рекурсия, или же рекурсивная функция — это такая функция, которая вызывает саму себя.
Рекурсию также можно сравнить с матрёшкой. Первая кукла самая большая, за ней идёт точно такая же кукла, но поменьше. Суть матрёшки состоит в том, что вы можете открывать её и доставать из неё точно такую же куклу, только немного меньше. Такой продолжительный процесс длится до тех пор, пока вы не дойдёте до последней куклы, которая и прервёт цикл. Так выглядит визуальная репрезентация рекурсии.
Не приведёт ли рекурсивная функция к бесконечному циклу?
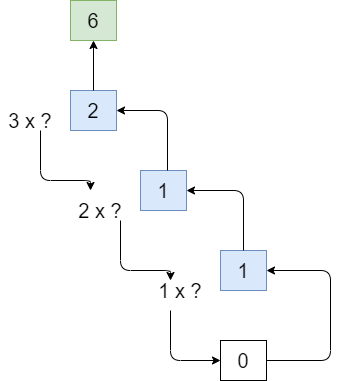
Вот пример кода того, как можно реализовать функцию обратного отсчёта с использованием рекурсии:
Как прервать рекурсию:
Проще говоря, рекурсия делает то же, что и код ниже:
Плюсы и минусы рекурсивных функций
Чтобы правильно описать плюсы и минусы, давайте взглянем на производительность рекурсии.
Плюсы:
Под этим подразумевается, что рекурсии, в сравнении с циклами, тратят меньше времени до завершения функции. Чем меньше строк кода у нас будет, тем быстрее функция будет обрабатывать вызовы внутри себя. Особенно хорошо это проявляется при буферизации данных, что позволяет оптимизировать и ускорить код.
В программировании мемоизация — это метод сохранения результатов выполнения функций для предотвращения повторных вычислений. Это один из способов оптимизации, применяемый для увеличения скорости выполнения программ. — Википедия
И всё же стоит отметить, что рекурсия не всегда выигрывает по скорости по сравнению с циклами.
Многие согласятся, что эта причина очень важна. Рекурсия проста в отладке из-за того, что она не содержит сложных и длинных конструкций.
Минусы:
Рекурсивные функции занимают значительный объём памяти во время своего выполнения. Это означает, что при каждом вызове функции в стек будет добавляться новый элемент, который будет занимать место до тех пор, пока функция не завершит работу, найдя ответ, либо пока не дойдёт до выполнения базового условия функции.
Что такое «стек»?
Стек — это такая структура данных, которая работает по принципу «Last In, First Out» (последним пришёл — первым ушёл). Таким образом, элемент «проталкивается» в стек и добавляется в его конец, а затем «выталкивается» из стека при удалении.
Стоит ли использовать рекурсии вместо обычных циклов?
Оба этих метода одинаково эффективны для решения задач, однако выбор одного из них зависит от типа проблемы, поставленной перед вами.
Рекурсии эффективны тогда, когда вы работаете с данными, которые слишком сложны, чтобы пройтись по ним с помощью обычных циклов. Стоит также не забывать о ценности памяти и уменьшении времени, идущем вкупе с рекурсивной функцией, в которой накопилось слишком много элементов.
Циклы так же эффективны в плане скорости и оптимизации, они занимают меньше памяти в стеке и их легче понять, потому что в теле цикла содержится больше информации о том, что происходит внутри.
Рекурсия вокруг нас: люди, соборы и капуста романеско
Спойлер: рекурсия есть не только в цифровом мире. Встречается она и в реальном. И намного чаще, чем вы думаете, — разная и интересная.
Валентина Палатурян для Skillbox
Про рекурсивные функции я узнала на уроках информатики. Потом долго считала рекурсию всего лишь отвлечённым понятием из программирования, далёким от реальной жизни. Почему-то в школе нам не рассказывают, что на самом деле явление это встречается в природе, науке, искусстве, а рекурсивные алгоритмы применимы даже для решения бытовых задач.
Что такое рекурсия
В программировании рекурсивная функция — это такая функция, которая вызывает себя из себя же самой, но с другими значениями параметров.
Примечание. Функция может вызывать себя и через промежуточные функции. Например, функция А запускает функцию Б, а та снова вызывает А.
Цепочка вызовов не может быть бесконечной, она должна прерваться и выдать ответ. Поэтому должен возникать крайний случай (или несколько), когда функции уже не нужно вызывать себя с другими параметрами (то есть погружаться ещё глубже), а можно сразу вернуть результат.
Звучит и правда сложно, но не пугайтесь — с примером станет понятнее.
Классический пример рекурсивной функции — вычисление факториала, то есть произведения натуральных чисел от 1 до N.
Здесь N=0 — это крайний случай: функция ничего не вызывает и сразу возвращает единицу (по определению, факториал нуля равен единице).
В более широком смысле рекурсией называют описание или изображение предмета, объекта, явления внутри самого себя. Рекурсивный принцип — это принцип самовоспроизведения и одновременно усложнения системы по одному и тому же алгоритму.
Тут-то и выясняется, что и нас, людей, тоже можно считать рекурсивными: ведь в клетке заложена информация обо всём организме, в ДНК записана информация о том, как синтезировать ДНК.
Фулстек-разработчик. Любимый стек: Java + Angular, но в хорошей компании готова писать хоть на языке Ада.
Рекурсия — не то же самое, что бесконечный цикл
Хотя её часто с ним путают. Понять разницу проще всего на примере. Предположим, ваш начальник издал приказ:
Это не рекурсия. Просто в ситуации, когда начальник не прав, мы попадём в бесконечный цикл вызовов.
Но можно внести небольшое изменение и получить рекурсию:
Приказ стал рекурсивным, потому что в одной из веток вызывает сам себя.
На обед у нас салат «Рекурсивный»: помидоры, огурцы, салат.
Рекурсию можно увидеть
И это очень красиво. Рекурсивные изображения, они же фрактальные паттерны или просто фракталы, — это рисунки или предметы, которые подобны сами себе: состоят из уменьшенных копий себя.
Подобным же образом выстроены кровеносные сосуды и нервы в организме животных. Свойствами фракталов обладают снежинки, а ещё — удивительная капуста романеско. Вот она на картинке ниже — ну разве не красавица? 😀
В архитектуре рекурсия встречается в облике готических соборов.
В этом соборе XIII века задействован один из характерных для готики приёмов: его окна украшены тонкими ажурными перегородками. Их основной узор — стрельчатая арка с кругом внутри, круг поддерживается двумя арками меньшего размера.
А вот рекурсивная версия того же узора — Собор Линкольна.
Здесь окно тоже выполнено в форме остроконечной арки с вписанным в неё кругом, а круг лежит на двух других арках. Вот только внутри каждой из этих арок — снова круг и две ещё меньших арки, а внутри них — ещё по одному кругу на двух меньших арках.
Другой пример архитектурной рекурсии — собор Святого Петра в Ватикане.
Джордж Херси, американский писатель и журналист, сравнивал его с китайскими шкатулками с секретом. По его словам, архитектурный комплекс состоит из одной макроцеркви, четырёх наборов того, что журналист назвал макси-церквями, 16 мини-церквей и 32 микроцерквей. А мог бы просто сказать, что собор рекурсивный.
В изобразительном искусстве рекурсия тоже отметилась — взять хотя бы «Триптих Стефанески» Джотто. На его центральной панели изображён кардинал Стефанески, которой держит в руках этот же триптих (на котором тоже изображён триптих и так далее).
А вот пример посвежее — литография «Рисующие руки» нидерландского художника XX века Маурица Эшера:
Чтобы увидеть рекурсию, необязательно идти в картинную галерею — просто посмотрите на герб России. Двуглавый орёл держит в правой лапе скипетр, который увенчан двуглавым орлом, а тот тоже держит скипетр, который… 🙂 В общем — вот:
Рекурсию можно услышать
В музыке есть композиции, которые тоже можно назвать рекурсивными. Американский физик и писатель Дуглас Хофштадтер в своей книге «Гёдель, Эшер, Бах: эта бесконечная гирлянда» рассказывает о рекурсии, приводя в пример джигу из «Французской сюиты №5» Баха.
В первой её части трижды повторяется мелодический переход из тональности соль мажор в ре минор: мелодия как бы вызывает сама себя, погружаясь всё глубже. А во второй части, наоборот, трижды поднимается от ре к соль.
Программисту это может напомнить вычисление факториала числа 3: функция трижды вызывает саму себя, затем трижды возвращается с промежуточными результатами вычислений, а затем — с итоговым.
В лингвистике рекурсией называют способность языка порождать вложенные предложения и конструкции. Например, предложение «Саша читает статью про рекурсию» можно достроить до «Лена смотрит, как Саша читает статью про рекурсию». А его, в свою очередь, превратить в «Ленин друг Петя не одобряет, что Лена смотрит, как Саша читает статью про рекурсию».
Принято считать, что рекурсия свойственна любому человеческому языку (сомнения пока есть только насчёт языка пираха, на котором разговаривают в бразильской части бассейна Амазонки), а распознавать и понимать её — едва ли не врождённая способность людей.
Чтобы доказать это, немецкие учёные даже ставили эксперименты на пятимесячных младенцах. Они измеряли активность головного мозга с помощью ЭЭГ — и сравнивали реакцию малышей на вложенные языковые конструкции, правильные и неправильные. Так как дети были настолько малы, что речь ещё не понимали, вместо слов им проигрывали последовательности звуков разной частоты. Причём частоты звука для связанных слов во вложенных конструкциях совпадали.
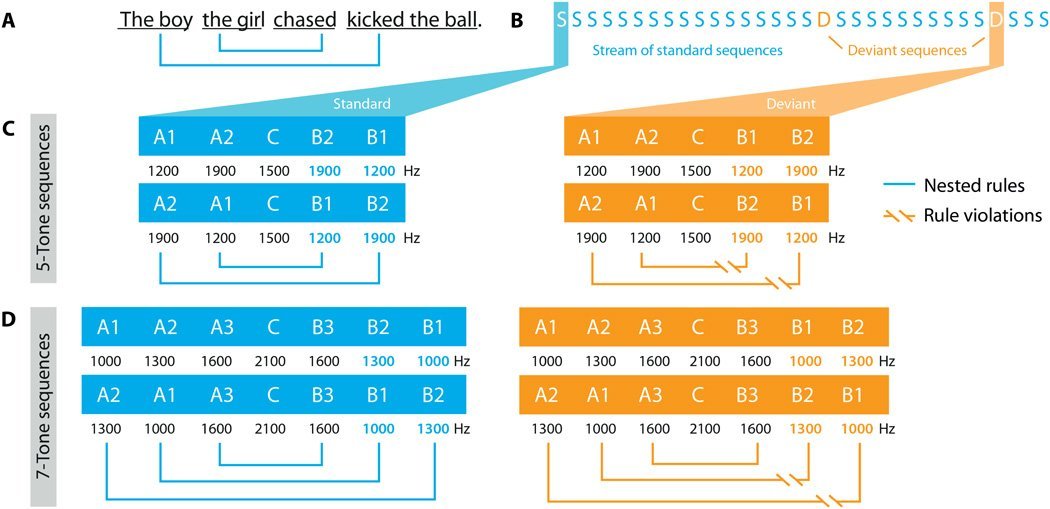
В предложении «Мальчик, за которым гналась девочка, пнул мяч» две связанные конструкции: 1) «мальчик пнул» и 2) «девочка гналась». Их обозначили звуками частотой 1900 и 1200 Герц и разделили коротким звуком в 1500 Герц. Слева — корректные, а справа — некорректные языковые паттерны. Кроме пятитоновых, проигрывались и семитоновые вложенные последовательности.
Научные подробности ищите в оригинальной публикации. Нам важнее выводы: эксперименты показали, что даже мозгу младенцев неправильные конструкции определённо не понравились.
Конечно, выборка (38 участников) слишком мала, чтобы распространять результаты на всё человечество, но теория интересная.
Рекурсивные алгоритмы легко смоделировать с помощью подручных средств
Возьмите, например, матрёшку. Все вложенные в неё куклы подобны кукле-шкатулке, кроме наименьшей, которая представляет собой базовый случай. То есть матрёшка — твёрдое воплощение рекурсии.
А если задаться целью поставить синюю точку на самой маленькой кукле, то можно буквально на пальцах реализовать рекурсивный алгоритм:
А вот алгоритм, для исполнения которого не нужны дополнительные предметы. Представьте, что вы сидите в последнем ряду длинного зала и хотите узнать, сколько всего в нём рядов. Конечно, можно встать и пересчитать их, но вам лень, а ещё вы уже знаете про рекурсию.
Так что вы спрашиваете соседа спереди, сколько перед ним рядов. Если он называет какое-то число, вы прибавляете к нему ещё два (один ряд — для соседа и один — тот, в котором сами сидите) и получаете ответ, а иначе — предлагаете этому самому соседу применить ваш гениальный алгоритм уже к его соседу спереди.
Если все участники процесса будут настроены доброжелательно, то в итоге очередь отвечать дойдёт до первого ряда и вам обратно по цепочке вернут результат — полученный с помощью рекурсивного алгоритма, между прочим. То есть:
И минутка предметного юмора
— Помнишь, Антоха желание проиграл? Так вот, я ему загадал, чтобы он два дня на все предметы, с которыми что-то сделал, клеил стикер с названием этого действия.
— И что, он на каждый новый стикер клеил другой с надписью «наклеил»?
Подытожим
Рекурсивные предметы и явления окружают нас повсюду. Рекурсию можно увидеть, услышать, потрогать руками. Рекурсия — это просто. Чтобы понять её, не обязательно разбираться с фракталами или фугами Баха. Объяснить рекурсию можно даже пятилетнему ребёнку. Просто прочтите ему стишок Андрея Усачёва:
Шёл по улице жучок
На груди блестел значок,
Нарисован был жучок,
И на нём висел значок,
Был ещё один жучок…
Что глядел я целый час
Был ли у жучка значок?
Был ли на значке жучок?
Тональность — музыкальный термин. Определяется тоникой (опорная, главная нота музыкального произведения) и типом лада (мажор или минор).
ЭЭГ — электроэнцефалограмма, регистрирует электрические сигналы клеток головного мозга.
Рекурсия. Беглый взгляд
Ниже речь пойдёт о старушке рекурсии, которую неплохо бы представлять, понимать и применять.
Примечание: Данная небольшая статья написана для беглого ознакомления с рекурсией, некоторыми примерами её применения и опасностями.
Определение
Для начала стоит сказать, что рекурсия относится не только к программированию. Рекурсия — это общее понятие, которое может быть присуще чему угодно и встречаться в повседневной жизни, но больше всего она распространена в информатике и математике. Для программистов же умение применять рекурсию — большой плюс в коллекцию полезных навыков.
Самая большая глупость — это делать то же самое и надеяться на другой результат.
Под рекурсией понимают процесс повторения элементов самоподобным образом. Объект обладает рекурсией, если он является частью самого себя.
Частным случаем рекурсии является хвостовая рекурсия. Если любой рекурсивный вызов является последней операцией перед возвратом из функции, то это оно.
Некоторые примеры
Рекурсию надо бы понять, а определение для этого подходит хуже, чем наглядные примеры. Для лучшего понимания, конечно, всё же следует прочитать определение, посмотреть на пример, снова прочитать определение и снова посмотреть на пример… Повторять, пока не придёт осознание.
Отличный пример вы можете найти тут.
Самое известное программисту применение рекурсии — задачи на вычисление чисел Фибоначчи или факториала. Давайте покажем, как это реализовать на языке C:
Тут же стоит отметить, что декларативная парадигма, в частности парадигма логического программирования, намного лучше позволяет понять рекурсию, так как там это обычное дело.
Fork-бомба
Примечание: Рекурсивное создание процессов крайне быстро (из-за экспоненциального роста их количества) заполняет таблицу процессов, что достаточно опасно для системы.
Reboot кнопкой после такого делать немного не приятно.
Для математика первой ассоциацией, скорее всего, будет фрактал. Фракталы прекрасны и приятно для глаза показывают свойства самоподобия.
Самые известные фракталы:
Ну и в повседневной жизни классическим примером являются два зеркала, поставленных друг напротив друга.
Углубимся глубже
Проста ли рекурсия? Однозначно нет. На вид кажется, что всё просто, однако рекурсия таит в себе опасности (А иногда она просто не понятна).
Вернёмся к примеру с вычислением чисел Фибоначчи. Сразу заметим, что возвращаемым результатом функции является вызов этой же функции, а если быть точнее, то сумма результатов вызова двух функций (именно поэтому рекурсия не хвостовая). Становится понятно, что второй вызов не произойдёт, пока не завершится первый (в котором также будет вызов двух функций). Тут же пытливый ум заметит, что из рекурсивной функции должен существовать «нормальный» выход, без самовызова, иначе мы познакомимся с переполнением стека вызовов — это один из ключевых моментов, который стоит держать в голове при работе с функциями вызывающими сами себя.
Заметим, что дерево вызовов получится большим, но максимальное количество вызовов в стеке будет заметно меньше (N-1 при N > 2, соответственно).
Рекурсивные алгоритмы довольно-таки часто встречаются при работе с деревьями, сортировками и задачами на графах. Так что, чтобы лучше вникнуть нужна практика и для этого не плохо подходит вышеупомянутое (в частности, бинарные или общие деревья. Их реализация не так сложна, а опыт работы с рекурсией получится не плохой).
Помимо этого хотелось бы упомянуть Ханойские башни, которые также отлично подойдут для ознакомления с рекурсивными задачами. На Хабре также был отличный разбор этой игры.
Для полноты картины обязательно надо упомянуть о борьбе с рекурсией.
Повышается производительность. Но это не значит, что с ней просто необходимо бороться, ведь применение рекурсии очевиднее, проще и приятнее, чем итерационные варианты.
Под силу ли побороть любую рекурсию?
Однозначно да. Любой рекурсивный алгоритм можно переписать без использования рекурсии, а хвостовую рекурсию же очень легко перевести на итерацию (чем и занимаются некоторые компиляторы для оптимизации). Это также относится и к итерационным алгоритмам.
Самый известный способ — это использование стека. Здесь подробнее, для интересующихся.
Заключение
Спасибо за прочтение статьи. Надеюсь, что большинство не знакомых с рекурсией получили базовое представление о ней, а от знающих людей, конечно, хочется услышать дополнения и замечания в комментариях. Не бойтесь рекурсии и не переполняйте стек!
UPD: Добавлен корректный пример хвостовой рекурсии.
Что такое рекурсия
Это дом, который построил Джек.
Рекурсия — важный элемент в математике и программировании. С её помощью можно упаковывать большие и сложные конструкции в маленькие и простые, а потом разворачивать обратно, когда нужно. Давайте выясним, как она устроена.
Дом, который построил Джек
Чтобы было понятнее, что такое рекурсия, возьмём стихотворение Самуила Маршака «Дом, который построил Джек»:
Вот дом,
Который построил Джек.
А это пшеница,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
А это весёлая птица-синица,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
Вот кот,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
Вот пёс без хвоста,
Который за шиворот треплет кота,
Который пугает и ловит синицу,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек. …
Смотрите, что в нём интересного: каждая часть стихотворения состоит из нового начала и точного повторения того, что уже было до этого. Сначала у нас был только дом, который построил Джек — это нулевой уровень рекурсии, или вложенности.
Вот дом,
Который построил Джек.
Обозначим его за [0] и дальше будем увеличивать это число для каждого уровня. Следите за уровнями.
А это пшеница,
Которая в тёмном чулане хранится [0]
Чтобы получить полноценное продолжение, нам нужно взять предыдущий уровень и подставить его сюда:
А это пшеница,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
А это весёлая птица-синица,
Которая часто ворует пшеницу,
[1]
Если мы будем разворачивать стих, то на первом проходе получим такое:
А это весёлая птица-синица,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
[0]
А на втором у нас уже появится полноценный стих:
А это весёлая птица-синица,
Которая часто ворует пшеницу,
Которая в тёмном чулане хранится
В доме,
Который построил Джек.
👉 Общее правило такое: когда есть рекурсия, её последовательно разворачивают на каждом шаге, пока не дойдут до нулевого уровня. Как только дошли — всё готово, рекурсия сделала своё дело. До этого момента она вызывает сама себя с новыми параметрами.
Рекурсия в программировании
Допустим, нам нужно посчитать сумму всех чисел от 1 до какого-то числа. Можно это сделать в цикле, а можно сделать универсальную функцию с рекурсией. Ей будет достаточно указать на входе число, до которого нужно всё посчитать, а она сама сделает всё остальное.
Сначала запишем это на JavaScript, а потом разберёмся с тем, как работает эта магия:
Затем мы организуем нулевой уровень — тот, где рекурсия начинается: if (x == 1)
А дальше идёт самое интересное — если мы не дошли до единицы, то мы берём значение x и складываем его с результатом этой же функции, но от предыдущего значения. Если мы, например, считаем rec(10), то эта команда сделает так:
Попробуйте сами вставить код в консоль и посмотрите на результат.
Особенности рекурсии
Так как рекурсия — это программа, которая вызывает саму себя, то при неправильном подходе рекурсия может использовать очень много памяти и машинных ресурсов. Чем глубже уровень рекурсии — тем больше ресурсов ей нужно.
Иногда программист увлекается рекурсией и забывает прописать выход из неё. В результате рекурсия бесконечно углубляется саму в себя, забирает в себя все ресурсы и программа падает. Говорят, что так образуются чёрные дыры, в которых всё исчезает.
Бывают моменты, когда рекурсия — это единственный способ выполнить нужную задачу. Например, при парсинге HTML-кода или для построения дерева зависимостей.
Что дальше
Теперь, когда мы достаточно знаем про рекурсию, то сможем сделать интересный новый проект. Например, чтобы наша программа сама решала судоку любой степени сложности или рисовала классные лабиринты.
Простыми словами о рекурсии
Dec 19, 2020 · 4 min read
В программировании рекурсия, или же рекурсивная функция — это такая функция, которая вызывает саму себя.
Рекурсию также можно сравнить с матрёшкой. Первая кукла самая большая, за ней идёт точно такая же кукла, но поменьше. Суть матрёшки состоит в том, что вы можете открывать её и доставать из неё точно такую же куклу, только немного меньше. Такой продолжительный процесс длится до тех пор, пока вы не дойдёте до последней куклы, которая и прервёт цикл. Так выглядит визуальная репрезентация рекурсии.
Не приведёт ли рекурсивная функция к бесконечному циклу?
Вот пример кода того, как можно реализовать функцию обратного отсчёта с использованием рекурсии:
Как прервать рекурсию:
Проще говоря, рекурсия делает то же, что и код ниже:
Плюсы и минусы рекурсивных функций
Чтобы правильно описать плюсы и минусы, давайте взглянем на производительность рекурсии.
Плюсы:
Под этим подразумевается, что рекурсии, в сравнении с циклами, тратят меньше времени до завершения функции. Чем меньше строк кода у нас будет, тем быстрее функция будет обрабатывать вызовы внутри себя. Особенно хорошо это проявляется при буферизации данных, что позволяет оптимизировать и ускорить код.
В программировании мемоизация — это метод сохранения результатов выполнения функций для предотвращения повторных вычислений. Это один из способов оптимизации, применяемый для увеличения скорости выполнения программ. — Википедия
И всё же стоит отметить, что рекурсия не всегда выигрывает по скорости по сравнению с циклами.
Многие согласятся, что эта причина очень важна. Рекурсия проста в отладке из-за того, что она не содержит сложных и длинных конструкций.
Минусы:
Рекурсивные функции занимают значительный объём памяти во время своего выполнения. Это означает, что при каждом вызове функции в стек будет добавляться новый элемент, который будет занимать место до тех пор, пока функция не завершит работу, найдя ответ, либо пока не дойдёт до выполнения базового условия функции.
Что такое «стек»?
Стек — это такая структура данных, которая работает по принципу «Last In, First Out» (последним пришёл — первым ушёл). Таким образом, элемент «проталкивается» в стек и добавляется в его конец, а затем «выталкивается» из стека при удалении.
Стоит ли использовать рекурсии вместо обычных циклов?
Оба этих метода одинаково эффективны для решения задач, однако выбор одного из них зависит от типа проблемы, поставленной перед вами.
Рекурсии эффективны тогда, когда вы работаете с данными, которые слишком сложны, чтобы пройтись по ним с помощью обычных циклов. Стоит также не забывать о ценности памяти и уменьшении времени, идущем вкупе с рекурсивной функцией, в которой накопилось слишком много элементов.
Циклы так же эффективны в плане скорости и оптимизации, они занимают меньше памяти в стеке и их легче понять, потому что в теле цикла содержится больше информации о том, что происходит внутри.