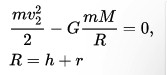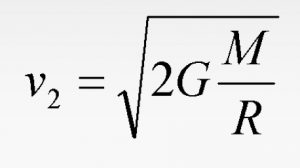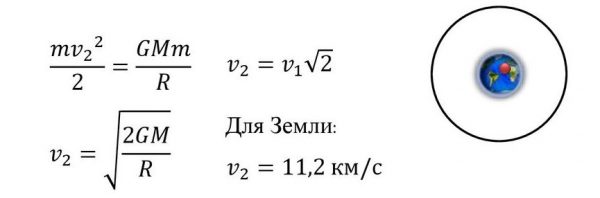Для чего нужна вторая космическая скорость
Вторая космическая скорость
Из школьного курса физики мы помним, что первая космическая скорость Земли – это показатель, которого необходимо достичь, чтобы объект мог выйти на эллиптическую орбиту вращения вокруг планеты. Это же, собственно, касается и любого массивного космического тела. В свою очередь, вторая космическая скорость – это предел, необходимый для того, чтобы полностью покинуть гравитационное поле планеты.
Вторая космическая скорость зависит от ряда параметров и для каждого космического объекта – отличается. Давайте рассмотрим, по какому принципу она вычисляется, и разберем примеры для крупных планет Солнечной Системы, Солнца и Луны.
Как рассчитать вторую космическую скорость
Вторая космическая скорость зависит от массы и радиуса небесного тела. Условно можно себе представить, что для ее расчета можно пойти от обратного решения задачи. То есть, вычислить скорость с какой объект будет падать на планету из космоса. По модулю это и будет вторая космическая скорость.
Итак, учитывая закон сохранение кинетической и потенциальной энергий при движении тел, можно вывести такую формулу в падающем объекте на небесное тело:
Где m – масса стартующего объекта, М – масса небесного тела, R – сумма радиуса планеты и высоты расположение объекта над поверхностью, G – гравитационная постоянная, V – искомая вторая космическая скорость. Таким образом, из формулы можно вычислить V:
Это и будет решение нашей задачи со знанием всего двух параметров – радиуса небесного тела и его массы.
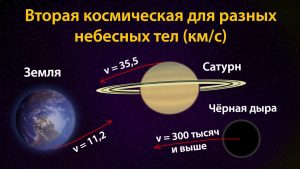
Вторая скорость для разных небесных тел
Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.
Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.
Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.
Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с.
Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.
Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.
Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.

Похожие статьи
Понравилась запись? Расскажи о ней друзьям!
Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
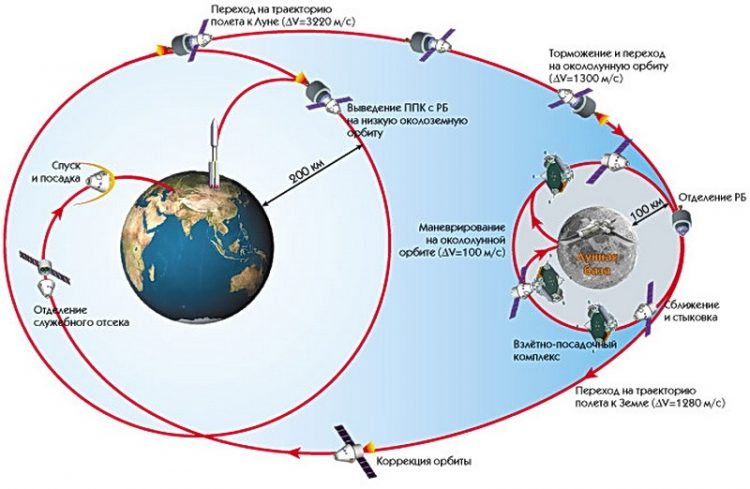
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
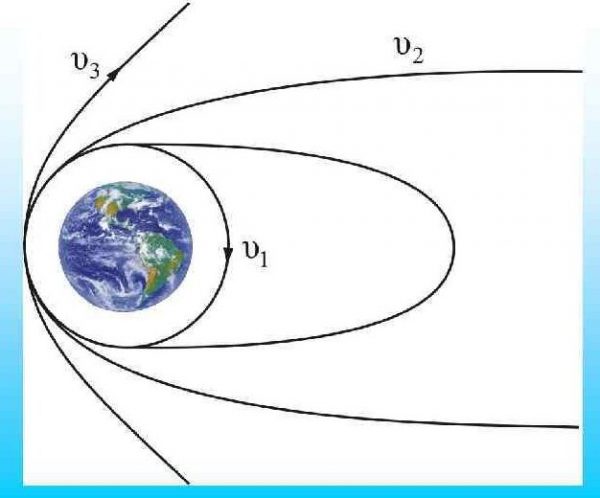
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
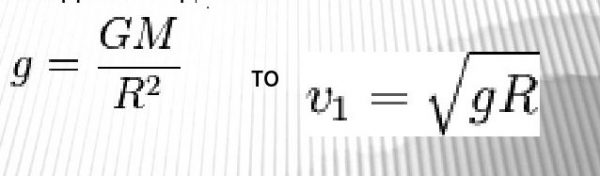
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
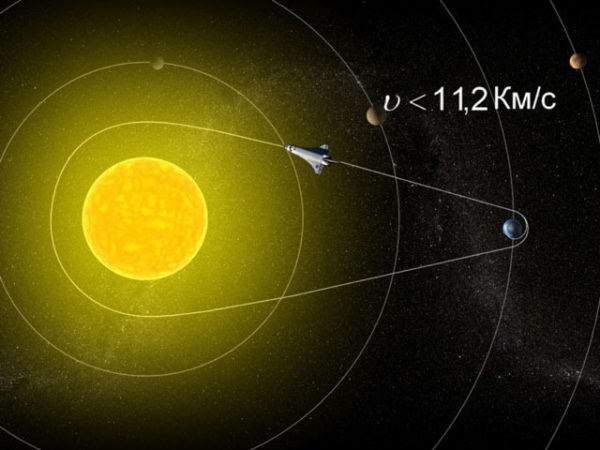
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Вторая космическая скорость
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания круговой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по дуге параболы относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой; если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.
Содержание
Вычисление
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v2 — вторая космическая скорость.
Решая это уравнение относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):
Вторая космическая скорость для различных объектов
См. также
Примечания
Ссылки
 Небесная механика Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Полезное
Смотреть что такое «Вторая космическая скорость» в других словарях:
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Параболическая скорость … Большой Энциклопедический словарь
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см … Большая политехническая энциклопедия
вторая космическая скорость — см. Параболическая скорость. * * * ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ, см. Параболическая скорость (см. ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ) … Энциклопедический словарь
Вторая космическая скорость — минимальная скорость v2, необходимая для того, чтобы космический летательный аппарат вышел из сферы гравитационного действия Земли и стал искусственным спутником Солнца. Выражается формулой: Вторая космическая скорость, где G гравитационная… … Астрономический словарь
вторая космическая скорость — antrasis kosminis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. escape cosmic velocity; second cosmic velocity vok. Entweichgeschwindigkeit, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
вторая космическая скорость — antrasis kosminis greitis statusas T sritis fizika atitikmenys: angl. escape cosmic velocity; second cosmic velocity vok. Entweichgeschwindigkeit, f; Entweichungsgeschwindigkeit, f; zweite kosmische Geschwindigkeit, f rus. вторая космическая… … Fizikos terminų žodynas
Вторая космическая скорость — наименьшая скорость (начальная), которую нужно сообщить телу у поверхности Земли, чтобы оно, преодолев действие земного притяжения, навсегда покинуло Землю. В. к. с. равна примерно 11,2 км/сек. Тело, обладающее В. к. с., движется по… … Большая советская энциклопедия
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Параболическая скорость … Естествознание. Энциклопедический словарь
ВТОРАЯ КОСМИЧЕСКАЯ СКОРОСТЬ — см. Космические скорости … Большой энциклопедический политехнический словарь
Космическая скорость — (первая v1, вторая v2, третья v3 и четвёртая v4) это мин … Википедия
Вторая космическая скорость
Из Википедии — свободной энциклопедии
Втора́я косми́ческая ско́рость (параболи́ческая ско́рость, ско́рость освобожде́ния, ско́рость убега́ния) — наименьшая скорость, которую необходимо придать стартующему с поверхности небесного тела объекту (например, космическому аппарату), масса которого пренебрежимо мала по сравнению с массой небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела и покидания замкнутой орбиты вокруг него. Предполагается, что после приобретения телом этой скорости оно более не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Параболической вторая космическая скорость называется потому, что тела, имеющие при старте скорость, в точности равную второй космической, движутся по параболе относительно небесного тела. Однако, если энергии телу придано чуть больше, его траектория перестает быть параболой и становится гиперболой. Если чуть меньше, то она превращается в эллипс. В общем случае все они являются коническими сечениями.
Если тело запущено вертикально вверх со второй космической и более высокой скоростью, оно никогда не остановится и не начнёт падать обратно.
Эту же скорость приобретает у поверхности небесного тела любое космическое тело, которое на бесконечно большом расстоянии покоилось, а затем стало падать.
Впервые вторая космическая скорость была достигнута коcмическим аппаратом Луна-1 (СССР) 2 января 1959 года.
Космические скорости
«Поехали!»
В 1957 году работа советских учёных, конструкторов, инженеров, рабочих, во главе с Сергеем Павловичем Королёвым, увенчалась блестящей победой: 4 октября они вывели на орбиту первый в истории искусственный спутник Земли. А 12 апреля 1961 года отправили в первый космический полёт человека — Юрия Алексеевича Гагарина. На весь мир прозвучало знаменитое гагаринское «Поехали!», и человечество вступило в космическую эру.
Космическая тематика стремительно вошла в моду. Естественно, появились новые темы и понятия — ракеты, скафандры, невесомость, первая космическая скорость, вторая космическая скорость. Все мальчишки нашего поколения в мечтах примеряли скафандр космонавта. О невесомости мы поговорим в другой раз, а пока рассмотрим космические скорости.
Что известно о космических скоростях простым людям
На телевидении есть передача, в которой весёлый молодой человек бегает по улицам и задаёт прохожим разные вопросы. За правильный ответ он вручает 1000 рублей. Однажды он задал такой вопрос: «Какую скорость надо развить, чтобы оторваться от Земли?» Первый встречный ответить не смог, и ведущий буквально клещами вытащил из второго ответ, который был признан правильным: «Вторую космическую».
Увы, молодой человек ошибся. Вернее, ошибся не он, а редакторы, придумывающие вопросы и ответы к ним. Точно так, как и редакторы, считают почти все, кто хоть отдалённо слышал про существование первой и второй космических скоростей.
На самом деле, чтобы оторваться от Земли, подходит любая скорость. Уже когда ребёнок подпрыгивает, он отрывается от Земли. Пусть ненадолго, но отрывается. И вообще, до Луны или до другого космического объекта можно добраться с любой скоростью. Для этого надо немного разогнаться, а потом поддерживать силу тяги двигателя, равную силе земного притяжения, и вы будете «бороздить просторы Вселенной» с постоянной скоростью. Более того, если представить, что какой-то чудак сумел построить лестницу до Луны, то вы сможете подняться туда просто пешком. Примерно так, как вы поднимаетесь к себе домой на третий этаж, только гораздо дольше.
А как же космические скорости? Космические скорости подразумевают, что ракета, достигнув их, дальше летит к намеченной цели по инерции, с неработающим двигателем. Это только в мультфильмах про космические путешествия показывают летящие ракеты с работающим двигателем. Но это исключительно для создания иллюзии движения.
Если же в реальных условиях двигатель у ракеты будет работать постоянно, то даже для полёта на Луну потребуется такое количество топлива, что его ни одна ракета не осилит.
Постреляем
Первая космическая скорость
Первая космическая скорость — это скорость, с которой надо горизонтально запустить объект, чтобы он стал вращаться вокруг Земли по круговой орбите.
Чем больше высота, с которой мы запускаем объект, тем меньше эта скорость. Например, Международная космическая станция летает на высоте 400 км со скоростью 7,6 км/с, а Луна — на расстоянии 384 500 км от Земли со скоростью 1 км/с. «Нулевой» высоте соответствует скорость 7,9 км/с, что обычно и называют первой космической скоростью.
Точно так же Земля вращается вокруг Солнца почти по круговой орбите со скоростью ≈ 30 км/с. Это и есть первая космическая скорость относительно Солнца на таком расстоянии от него.
Если скорость спутника чуть больше первой космической для его высоты, его орбита будет эллипсом. Все спутники вокруг Земли и планеты вокруг Солнца движутся именно по эллипсам. И орбиты комет — тоже эллипсы, только очень вытянутые, так что кометы улетают по ним «в даль тёмную», лишь изредка возвращаясь к Солнцу «погреть бока».
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Вторая космическая скорость
Вторая космическая скорость — наименьшая скорость, которую необходимо придать космическому аппарату для преодоления притяжения планеты и покидания замкнутой орбиты вокруг неё.
Предполагается, что аппарат не вернётся на планету, улетит в бесконечность. На самом деле тело, имеющее около Земли такую скорость, покинет её окрестности и станет спутником Солнца. Вторая космическая скорость в \(\sqrt <2>≈ 1<,>4\) раза больше первой космической.
Третья космическая скорость
Третья космическая скорость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть притяжение не только Земли, но и Солнца, и покинуть пределы Солнечной системы.
Космические достижения
Первый искусственный спутник Земли был шариком диаметром 58 см и передавал только звуковой сигнал «бип-бип-бип». Но первая космическая скорость была достигнута! А всего через год, 2 января 1959 года, космический аппарат «Луна-1» полетел, естественно к Луне, со второй космической скоростью.
Пока с наибольшей скоростью 16,26 км/с покидала Землю автоматическая межпланетная станция «Новые горизонты», запущенная в США 19 января 2006 года. Относительно Солнца её скорость составляла 45 км/с — благодаря тому, что запускалась она в сторону движения Земли по орбите.
Конические сечения
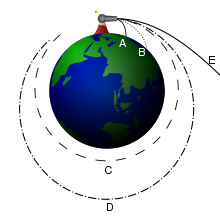
Вернёмся к движению тела вокруг одного источника притяжения, например Солнца. Если тело запустить с первой космической перпендикулярно направлению на Солнце, оно полетит по окружности. Если запустить его в любом направлении, только не на само Солнце, со скоростью меньше второй космической, орбита будет эллипсом. При запуске со второй космической получится парабола. Если запустить с ещё большей скоростью, получится гипербола.
Эти кривые можно увидеть, пересекая конус плоскостью. Если ось конуса перпендикулярна плоскости, в пересечении получится окружность. Будем постепенно менять угол наклона плоскости к оси конуса. Линия пересечения превращается в эллипс, причём чем больше угол наклона, тем более вытянутым получается этот эллипс. Продолжим наклонять секущую плоскость до тех пор, пока она не станет параллельной одной из касательных плоскостей конуса. В этот момент линия пересечения — парабола. Наклоним ещё — получится гипербола.
Художник Мария Усеинова
1 Подробнее об этом читайте в «Квантике» №11 за 2016 год, с. 2–5.