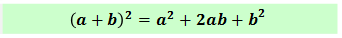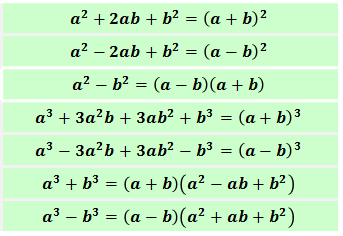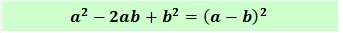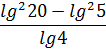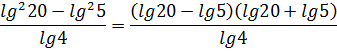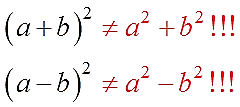Для чего нужны формулы

Математические формулы – жизнь среди чисел

Решение задачи зависит от правильного подхода и умения применять знания.

Математические формулы – это плод многолетних трудов массы ученых, современным же людям остается найти в массе комбинаций ту самую, единственно подходящую.

Математика – наука, которая кажется незаметной, но она сопровождает нас всю сознательную жизнь. С числами и формулами нас знакомят в школе, а жизнь находит применение базовым знаниям.

Не каждый человек имеет способности к математике, но нормативы и контрольные, экзамены и тестирования приходится сдавать практически всем. Сложные и простые задачи приходится решать ежедневно, тем более студентам и школьникам. Решение дается не всегда просто, ведь строгие педагоги спешат дать знания и проверить степень усвоения материала.

Математические формулы – простой ключ к решению задач

Обширная и интересная наука все развивается, усложняясь и представляя новые решения старых вопросов. Ученые веками изучали закономерности и выводили формулы, доказывали теоремы и рассуждали о смысле аксиомы. Огромные труды, многовековые познания современные студенты должны освоить в короткий промежуток времени. Это невозможно.

Все осознают, что объять необъятные познания в области науки невозможно, поэтому курс математики и подразделов данной науки дает лишь поверхностное понимание законов и правил, лишь самые востребованные знания.

С первого класса и до конца жизни человек изучает формулы по математике, иногда даже не осознавая того. Их настолько много, что запомнить весь массив не удастся никогда. На выручку идут специальные сборники, классифицированные по различным характеристикам, в которых также нужно уметь ориентироваться. Применение правильной формулы дает простое решение задачи.

Как найти ключ к решению?

Еще раз следует отметить, что формул много, поэтому справочная информация выручит в трудный момент. Математические формулы разделяются соответственно разделам обширной науки, и состоят из определенного количества параметров, зная часть из которых, можно найти решение.

Умение оперировать познаниями в математике необходимо, поэтому мы собрали самые часто используемыеформулы для вас, ссылки на которые есть в разделе Полезные материалы для изучения математики.

Применение математических формул

Математику невозможно вычленить из смежных наук – физики, информатики и т.п. Применение формул иногда настолько неожиданно, что трудно поверить, что этот результат возможен лишь благодаря «скучной» науке под названием «математика».

Математические формулы в процессе эволюции своего назначения претерпевали изменения, и связано это было с изменением понимания назначения самих формул. Числа давно уже перестали быть просто числами, а стали делиться на элиту в виде простых чисел, и на все остальные цифры. Когда любое число стало возможным представить в виде двух простых, а их, в свою очередь, представить кодированными символами, то и методы действий над ними тоже немного изменились. Не секрет, что каждый человек, работающий в сфере чисел, имеет свои наработки и взгляды на алгебраические формулировки. Суть в том, что как раз из этого и возникают предпосылки к возникновению новых формул и трактовок к их пониманию. Как бы ни были нам в прошлом дики массивы чисел, сейчас это норма, и массивы массивов только помогают в развитии других аспектов математических формул, например, в криптографии.

Студенческие годы пройдут, и экзамены будет устраивать сама жизнь. Научитесь оперировать исходными данными и применять формулы. Эти навыки позволят успешно развивать свою жизнь, правильно распоряжаясь своими ресурсами.

Источник

Исследовательская работа по математике на тему «Для чего нужны математические формулы»

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Муниципальное бюджетное образовательное учреждение «Школа №1»

Для чего нужны математические формулы

(Или, как вычислив площадь и объем кабинета, определить соответствие учебного кабинета санитарным правилам и нормам)

Работу выполнили: Кудряшов Эльман, Шумилов Роман ученики 5Б класса

Руководитель: Маслова М.Б.,

учитель информатики и математики

Оглавление

Математика представляет собой собрание выводов, которые могут быть применены к чему угодно.

Введение

Изучая математику, мы познакомились с геометрическими фигурами «прямоугольник» и «параллелепипед». Мы обратили внимание, что учебные кабинеты имеют форму параллелепипеда, а стены, пол и потолок – это прямоугольники. Как математические формулы могут пригодиться нам в жизни? Для чего они могут быть использованы?

На эти вопросы помогут нам ответить санитарные правила и нормы, а математические формулы помогут рассчитать размеры и объемы учебных кабинетов, в которых мы занимаемся.

Очень часто можно слышать, что математика скучная наука и некоторые ученики, говорят, что в жизни формулы математики не пригодятся. Это первое заблуждение, которое мы хотим опровергнуть. А, во-вторых, соблюдение санитарных и гигиенических норм позволит сохранить здоровье учащихся.

Эти два момента очень важны, потому что понимание того, для чего нужны формулы повысит интерес к математике, знание санитарных норм поможет сохранить здоровье.

Объектом исследования являются учебные помещения.

Формулы площади прямоугольника и объема параллелепипеда. Классные кабинеты № 16, 26, 28.

Исследовать соответствие учебных кабинетов СанПиНам, используя математические формулы.

Изучить учебную литературу по данной теме.

Провести измерение учебных кабинетов №№ 16, 26, 28 и вычислить их объем и площадь.

Вычислить объем и площадь, которые приходятся на 1 учащегося в каждом из кабинетов.

Используя измерения и простейшие математические вычисления, определить температуру и влажность воздуха в кабинетах.

Определить соответствуют ли размеры нашего класса нормам СанПиН.

Мы предполагаем, что, используя формулы для вычисления объёма прямоугольного параллелепипеда и площади прямоугольника, можно узнать, соответствуют ли размеры нашего класса нормам СанПиН.

— Изучение учебной литературы и СанПиН.

Глава 1. Общие сведения

1.1 Описание формул площади прямоугольника и объема прямоугольного параллелепипеда.

Как можно измерить площадь фигуры?

Измерить площадь фигуры – значит подсчитать, сколько единичных квадратов в ней помещается.

1.2 Основные положения санитарных правил и норм (СанПиН)

Глава 2. Измерение и вычисление основных параметров учебных кабинетов

В нашем классе обучаются 24 человека. Для исследований были выбраны кабинеты №16, №26, №28, в которых наш класс занимается чаще всего. Измерения кабинетов выполнялись с помощью рулетки.

Вычисление площади учебных кабинетов и расчет количества см 2 на 1 учащегося:

S – площадь пола кабинета

Количество см 2 на 1 учащегося =

Таблица вычисления площадей

Вычисление объема учебных кабинетов и расчет количества см 3 на 1 учащегося:

Количество см 3 на 1 учащегося =

Таблица объемов учебных кабинетов

Измерение температуры воздуха в кабинетах и расчет влажности.

Температура в помещении измеряется с помощью обычного ртутного термометра и записывается. Затем головку термометра необходимо плотно обернуть мокрой марлей или ватой и спустя 10 минут еще раз измерять температуру. Далее из температуры “сухого” термометра вычитаем температуру “мокрого”, а по разнице температур с помощью специальной (психометрической) таблицы определяем влажность воздуха в помещении.

Таблица температуры и влажности воздуха в учебных кабинетах

Заключение

Наше исследование показало, что любые, даже самые простые, математические формулы могут пригодиться в повседневной жизни человека.

Полученные результаты показали, что при небольшом недостатке площади на 1 учащегося в кабинетах № 26 S =20175 см 2 /уч. и № 28 S =20060 см 2 /уч. при норме 25000 см 2 /уч., объем помещений полностью удовлетворяет и даже превосходит требуемые нормы.

Температура и влажность воздуха в помещениях меняется в течение дня. Температура изменяется не значительно на 1-2 градуса, максимальное изменение в 5 градусов. Такие колебания температуры вызваны тем, что в каждом из кабинетов проходит разное количество уроков в день, чем больше уроков, тем выше колебания температуры. Регулярное проветривание кабинетов во время перемен позволит снизить колебание температуры. Надо отметить, что в кабинете № 28 утренняя температура ниже нормы на 2 0 С, но в течение дня она повышается до нормы.

Влажность воздуха так же изменяется в течение дня. К 14-00 влажность воздуха превышает норму на 10%-15%. Это связано с тем, что занятия заканчиваются, начинается активное проветривание и уборка помещений.

В целом, можно сделать вывод, что, не смотря на то, что наша школа была основана в 1898 г. и возраст основного здания, в кабинетах которого проводились исследования, более 100 лет, санитарные условия комфортны для учеников и не опасны для их здоровья.

Литература

1. Математика. 5 класс: учебник для учащихся общеобразовательных организаций/ А.Г.Мерзляк, В.Б. Полонский, М.С. Якир. – М.: Вентана-Граф, 2015г.

2. Постановление Главного государственного санитарного врача РФ от 29.12.2010 N 189 (ред. от 24.11.2015) «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (Зарегистрировано в Минюсте России 03.03.2011 № 19993), Документ предоставлен КонсультантПлюс, www.consultant.ru. Дата сохранения: 10.01.2016

3. Касьянов, В.А. Физика. 10 класс: Учебик. Для общеобразовательных учреждений. – 5-е изд., дораб. – Дрофа, 2003.

4. Шамшина Е.А., Гуреева Е.М. Интегрированный урок «Влажность воздуха» (физик и литератор)//www.openclass.ru/io/10/shamshina//Интернет и образование Июль, Том 2009, №10.

Источник

Что такое формулы и как их понимать?

Изначально, формулы были придуманы математиками для того, чтобы описать простые физические явления. Например формула скорости: скорость = путь/время. Эта формула говорит о том, что если двигаться с одинаковой скоростью, то за определенное время мы пройдем определенное расстояние. То есть она показывает связь между двумя изменяющимися величинами: путь и время. Если же одно и то же расстояние два человека пройдут с разной скоростью, то они потратят на это разное время, и первым финиширует тот, кто шел с большей скоростью.

Таким образом, формулы нужны для более короткой записи (математическими символами или буквами) взаимосвязей между некоторыми величинами (смотрите пример в статье).

Решение заданий с формулами обычно подразумевает нахождение какой-либо величины, зная остальные величины входящие в формулу.

Закон Ома выражается формулой: U = I•R, где U – напряжение в Вольтах, I – сила тока в Амперах, R – сопротивление в Омах. Зная, что сила тока равна 2 А, а сопротивление равно 10 Ом, найдите напряжение.

Все, что требуется в данном задании – подставить вместо букв их значения и посчитать. U = 2 • 10 = 20 В.

Встречаются задания и посложнее. Например:

Площадь четырехугольника находится по формуле: S = 1/2 d₁d₂ Sinα. Где d₁ и d₂ – диагонали четырехугольника, α – угол между ними. Вычислите Sinα. S = 21, d₁ = 7, d₂ = 15.

Для начала нужно выразить величину, которую нужно найти (то есть, чтобы эту величину и остальные величины разделял знак равно). Для этого нужно избавиться от лишних величин, стоящих возле Sinα.

Разделим обе части на 1/2 d₁d_2. В результате получим: = Sinα.

Теперь осталось подставить числа и посчитать: Sinα = = 0,4.

Первым действием разделим обе части на G, чтобы масса была отделена от других величин знаком равно.

F : G = m

F : = m

F • = m

= m

Теперь подставляем численные значения и находим наконец-то массу:

= m

Таким образом происходит решение задач на расчет по формулам.

Источник

Формулы сокращённого умножения

Формулы сокращённого умножения необходимы во всех разделах математики. От элементарной до высшей. Они применяются практически везде — в упрощении выражений, решении уравнений и неравенств, сокращении дробей, вычислении пределов, решении интегралов — список можно продолжать ещё долго…

Следовательно, нужно основательно разобраться с этими формулами. Понять, откуда они берутся, зачем они нужны, как их применять на практике и, самое главное, как их запомнить. А запомнить всё-таки придётся, да…

Квадрат суммы, квадрат разности, разность квадратов, куб суммы, куб разности, сумма кубов, разность кубов — что за звери?

Итак, вот они, формулы сокращённого умножения:

Эти семь формул — полный джентльменский набор. Последние две формулы (сумма и разность кубов) записаны не так как в большинстве учебников, а наоборот — справа налево. Это не просто так.) Любая формула в математике работает в обоих направлениях — как туда, так и обратно. Именно такая запись наиболее наглядно показывает, откуда берутся формулы сокращённого умножения.

Они берутся из… умножения. Вот ведь удивил, да?) Что ж, смотрите сами. Берём, например, самую первую формулу по списку:

Вот и все дела. Самое обычное перемножение скобок и приведение подобных. Именно так и получаются все формулы сокращённого умножения. Сокращённое умножение — потому, что в самих формулах нет раскрытия скобок и приведения подобных. Эти промежуточные действия сокращены. Сразу дан готовый результат. Пользуйтесь на здоровье!

Эти формулы надо знать наизусть. Без знания первых трёх формул, с квадратами, даже не мечтайте о тройке! Без всех остальных (с кубами) — о четвёрке и выше. Нет-нет, бросаться зубрить весь этот список прямо сейчас мы не будем.) Об этом позже. Пока просто знакомимся.)

Зачем нужны формулы сокращённого умножения?

Полезная вещь первая — самая очевидная. Это быстрое (т.е. сокращённое) умножение многих алгебраических выражений без промежуточных выкладок. Меньше выкладок — меньше и ошибок. Но это не самая главная полезная вещь! А вот вторая.

Сравним два равенства:

Для математики эти два равенства абсолютно одинаковы. А вот для нас с вами — не совсем. Возьмём первую запись, слева направо:

Это самое обычное умножение скобок, не более того. Никаких принципиально новых возможностей. А теперь возьмём второй вариант того же равенства, справа налево:

А вот такая запись резко повышает уровень вашей математической культуры! Почему? Потому, что такая запись формулы, справа налево, — это разложение на множители! А разложение на множители — процедура поважнее простого умножения, да…) Сомневаетесь? Не надо. В соответствующей теме подробно расскажу.)

И такое разложение на множители имеет место быть во всех формулах сокращённого умножения! Почему? Давайте внимательно посмотрим на наш список. В левой части каждой формулы мы увидим перемножение скобок:

Стало быть, левая часть каждой формулы разложена на множители, а вот правая часть — нет. Список, что приведён выше, — это, действительно, всего лишь сокращённое умножение. Но! Стоит только поменять местами левую и правую части каждой из формул, как тот же самый список становится формулами разложения на множители!

Для полного понимания перепишу этот список ещё разок, но справа налево. Вот так:

Такая обратная запись формул сокращённого умножения идеально подходит для разложения на множители многочленов, для сокращения алгебраических дробей и для решения самых разнообразных примеров. Но есть существенная проблема. Как их запомнить?

Запоминаем формулы сокращённого умножения! Секретные приёмы…

С выражениями (a+b) 3 и (a—b) 3 всё то же самое — куб суммы и куб разности соответственно.

Надеюсь, что названия сумма кубов и разность кубов у вас уже не вызовут недоумения?

А вот теперь начинается самое сложное — запоминание самих формул, со всеми этими выражениями. К сожалению, здесь тот самый случай, когда без механической памяти не обойтись. Это огорчает.

Однако здесь у нас с вами тайные знания! Эти знания помогут вам побыстрее сориентироваться во всех этих скобках, плюсах/минусах, квадратах/кубах, сведя механическую зубрёжку к минимуму. Читаем дальше и вникаем.

Итак, начинаем с квадрата суммы:

Просто медитировать, сверля формулу взглядом, будет недостаточно. Для лучшего запоминания настоятельно рекомендую выучить (да-да, именно выучить!) словесную формулировку:

Квадрат суммы двух выражений равен квадрату первого выражения ПЛЮС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.

Эта мантра реально облегчает жизнь во многих разделах школьной математики! Да и в институте, при работе со всякими там пределами да интегралами, тоже. Ещё не раз вспомните эту формулировку добрым словом!)

Если вы запомнили квадрат суммы, то дальше будет проще. Можно включать логику и здравый смысл. Переходим к квадрату разности:

Сравните с квадратом суммы! Нашли отличие? Да! Перед удвоенным произведением появился минус. Ведь должен же он где-то появиться?! Перед a 2 и b 2 он появиться никак не может, ибо любое число в квадрате есть число положительное. Остаётся только серединка.) Для понимания рекомендую просто перемножить скобки сами на себя да привести подобные. И тогда у вас пропадут все вопросы.

В словесной расшифровке:

Квадрат разности двух выражений равен квадрату первого выражения МИНУС удвоенное произведение первого выражения на второе ПЛЮС квадрат второго выражения.

Эта формула обычно и так легко запоминается. Единственное, можно случайно влепить в скобки два плюса или два минуса. Но тогда это уже будут квадрат суммы и квадрат разности. А это — совсем другие формулы…

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.

Переходим к следующей группе формул — к сумме и разности кубов:

Приём для запоминания здесь следующий. В первых скобках (маленьких) знак совпадает со знаком в исходном выражении: плюс-плюс, минус-минус. А вот во вторых (больших) скобках — меняется на противоположный. Причём меняется не перед квадратами, а снова посерединке! Квадраты a 2 и b 2 — положительные!

Кстати, посмотрите внимательнее на большие скобки в каждой из формул и сравните с формулами квадрата суммы и квадрата разности!

Нашли отличия? Да! В кубах не хватает двойки посерёдке. Именно по этой причине выражения в больших скобках

часто называют неполным квадратом суммы/разности.

А теперь можно и шаблонные словесные формулировки из учебников привести:

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Остаётся последняя парочка — куб суммы и куб разности:

Эти две формулы встречаются в заданиях пореже предыдущих пяти, но знать их тоже не помешает, да. Претендуете на пятёрку? Тогда читаем дальше!

Итак, как запомнить куб суммы? Во-первых, все знаки в формуле — плюсы! Оно и естественно. Ведь мы же перемножаем только положительные выражения, так с какого перепугу минусам-то взяться? Первое и последнее слагаемые — чистые кубы первого и второго выражений. А вот по центру — утроенные произведения.

Но и это ещё не всё! Смотрите-ка, какая интересная штука: сумма степеней a и b в каждом из слагаемых всегда равна трём! Например:

Такой порядок хорошо помогает не запутаться.)

Если вы уловили принцип запоминания куба суммы, то куб разности запомнится без проблем. Всё то же самое, только минусы надо правильно расставить. А это очень легко сообразить! Какая переменная у нас с минусом? Правильно, переменная b! Следовательно, в слагаемых, где b стоит в первой степени и в кубе — будет минус. Ибо любой минус в нечётной степени всегда даёт минус. А вот минус в квадрате (b 2 ) даст плюс. И все дела.)

Разумеется, изложенные выше советы — это не жёсткие правила математики. Это просто практические приёмы, помогающие более быстрому и комфортному запоминанию. Чисто для себя. Куда уж лучше, чем механическая зубрёжка, правда?)

Но, как ни крути, самый надёжный способ запомнить эти формулы — решать побольше примеров. Тогда весь этот перечень запомнится очень быстро. Сам собой, можно сказать.

Ну что, потренируемся?)

Примеры на формулы сокращённого умножения.

Начнём с самого простого — с прямого применения формул. Для разминки.)

Преобразовать в многочлен:

Сразу видим квадрат скобок. А в скобках — сумму. Значит, работаем по самой первой формуле, вот этой:

Идём дальше: «Плюс удвоенное произведение первого выражения на второе…». Удвоенное — это умножение на двойку. Первое выражение — это 5x, второе — это 4y. Продолжаем:

Практически всё. Осталось «причесать» удвоенное произведение (перемножить 2∙5∙4) и получим окончательный ответ:

Это было разминочное задание. А теперь примерчик посерьёзнее.

Разложить на множители:

Что, внушает? Опять смотрим на наш список. Но не на тот, что в начале урока (для умножения), а на второй, для разложения на множители. Вот на этот:

Тут, разумеется, нашего выражения нет. Ну и что? Здесь важно понимать, что под буквами a и b может скрываться всё что угодно — и числа, и другие буквы, и более сложные выражения. Поэтому смотрим на список и ищем похожую формулу. И зацепкой будут степени переменной.

В нашем выражении есть x 2 и просто x. Ясное дело, отбрасываем все формулы с кубами — у нас их явно нет. Далее выкидываем из рассмотрения формулу разности квадратов: там нет переменных в первой степени, только квадраты. А у нас — есть.

Остаются первые две формулы — квадрат суммы или квадрат разности. Уже проще, не так ли? Осталось сообразить, что в формуле квадрата суммы — только плюсы. А в нашем выражении в серединке стоит минус. Стало быть, похожая формула — это квадрат разности.

Но не факт, что квадрат разности сработает, совсем не факт… Наша задача — убедиться, что предложенное выражение 4x 2 –20x+25 точно соответствует квадрату разности. Только тогда у нас появится возможность записать и правую часть равенства (т.е. разложение на множители).

Для удобства я перепишу формулу и исходное выражение прямо одно под другим:

Всё? Можно записывать разложение? Пока нет.

Нужна последняя, контрольная проверка по выражению 20х. Надо убедиться, что наши 20х точно соответствуют удвоенному произведению 2ab.

Итак, затаив дыхание составляем удвоенное произведение первого и второго выражений:

Ура! Совпало! Значит, наше выражение — это действительно квадрат разности 2х и 5. Вот теперь можно со спокойной душой записывать ответ:

Идея ясна? Сначала ищем в списке похожую формулу, а затем сверяем с ней выражение, предложенное в задании, на полное соответствие. Если повезло и всё совпало, то записываем ответ. Если не повезло, то, значит, раскладывать надо как-то иначе.

Это были самые простые примеры, для младшеньких. А теперь переместимся в старшие классы, с их синусами да логарифмами. Да-да, старшеньким формулы сокращённого умножения тоже бывают нужны!

Например, такое задание:

Вся мощь тригонометрии слабо помогает в этом примере. Только алгебра седьмого класса и спасает, да…

Конечно, это выражение сильно смахивает на квадрат разности. Вот и пробуем применить эту формулу к нашему выражению! Что будет скрываться под буквами a и b? Конечно же, cos 2 x и sin 2 x. Удвоенное произведение, ясен перец, будет 2cos 2 x∙sin 2 x, как, собственно, в нашем выражении и записано. Смело сворачиваем нашего монстра в квадрат разности по формуле:

А вот теперь и тригонометрия в игру вступает! Что у нас в скобочках? У нас в скобочках косинус двойного угла!

Пример не подарок, прямо скажем… Логарифмические формулы явно не катят, да и сами логарифмы ровно не считаются… Проверим на алгебру? Числитель явно намекает на применение формулы разности квадратов.

В роли a и b у нас логарифмы. Ну и что? Это формулу никак не портит, ибо законы алгебры работают во всей математике. Смело заменяем числитель дроби на произведение скобок и пишем:

А вот теперь и логарифмические формулы заработали! В первых скобках (разность) получается lg4, который и сокращается благополучно со знаменателем. А во вторых скобках (сумма) будет lg100. Что по свойствам логарифмов есть 2.

Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда ученик глубоко погружён в синусы/косинусы да логарифмы, разложение на множители просто не приходит в голову…

Посему практический совет:

Проверяем замороченные примеры на алгебру седьмого класса! В частности, на формулы сокращённого умножения.

О типичном ляпе, который сразу же показывает блистательное отсутствие хоть какого-то понимания. Ляп настолько часто встречается, что хочется заявить громко:

И запомните это крепко-накрепко!

Формулы — штука жёсткая! Раз требуют удвоенного произведения 2ab, помимо чистых квадратов, значит спорить бессмысленно. Напишете такое на контрольной — будьте готовы получить заслуженную двойку! Такого не прощают. Вот так.

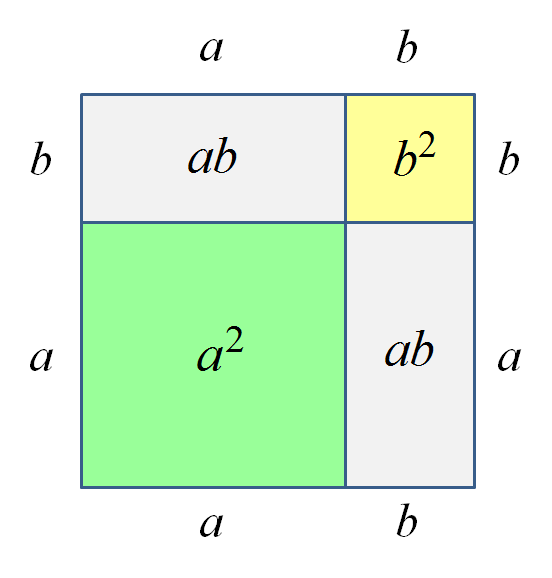
Наглядный пример на добрую память с квадратом суммы. Всё-таки картинки иногда проливают свет на очень многие волнующие вопросы. Нарисуем в тетрадке квадрат со стороной a+b. Можно по клеточкам. Допустим, для конкретики, a — это 4 клетки, a b — это 2 клетки.

Упражнение для интересующихся: аналогичным образом доказать геометрически (т.е. через квадраты и прямоугольники) две другие формулы сокращённого умножения с квадратами — квадрат разности и разность квадратов. Попробуйте! Интересно.)

1. Преобразовать в многочлен стандартного вида:

Источник