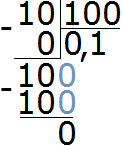Для чего нужны проценты в математике

Проценты

Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных таблицах вавилонян содержатся задачи на расчет процентов. До нас дошли составленные вавилонянами таблицы процентов, которые позволяли быстро определить сумму процентных денег.

Были известны проценты и в Индии. Индийские математики вычисляли проценты, применив так называемое тройное правило, т. е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов.

Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.

В средние века в Европе в связи с широким развитием торговли особо много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет фирмы.

Впервые опубликовал таблицы для расчета процентов в 1584 году Симон Стевин – инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий в том числе – особой записи десятичных дробей.

Употребление термина «процент» в России начинается с XVIII в. Это понятие впервые ввел Пётр I. Но считается, что подобные вычисления начали применяться в Смутное время, как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек.

Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область их применения расширилась.

Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буквы t в наклонную черту произошел современный символ для обозначения процента.

Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошел в результате нелепой опечатки, совершенной наборщиком. В 1685 году в Париже была опубликована книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.

Источник

Проценты

Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.

Что такое процент?

В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например, от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% = = 0,01

Как найти процент?

Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.

Например, найти 2% от 10 см.

А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.

Итак, делим число 10 на знаменатель дроби

Получили 0,1. Теперь 0,1 умножаем на числитель дроби

Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:

Значит 2% от 10 см составляют 2 мм.

Пример 2. Найти 50% от 300 рублей.

Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.

Итак, делим 300 рублей на 100

Теперь полученный результат умножаем на 50

Значит 50% от 300 рублей составляет 150 рублей.

Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.

В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.

Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?

Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32

Ответ: 384 костюмов нового фасона выпустила фабрика.

Второй способ нахождения процента

Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.

Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.

Запись 50% заменяет собой запись , а если перевести эти в десятичную дробь, то мы получим 0,5

Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5

Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %

Нахождения числа по его проценту

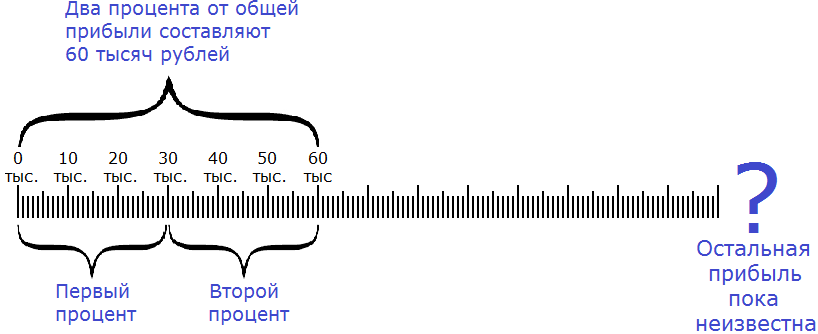
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Источник

Как решать задачи с процентами

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

40 : 0,16 = 40 · 100 : 16 = 250

Ответ: 250 задач собрано в этом учебнике.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

Ответ: в классе 40% девочек.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

А можно воспользоваться формулой:

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?

Как решаем: можно найти 12% от 110:

Прибавить к исходному числу:

110 + 13,2 = 123,2 рубля.

Или можно воспользоваться формулой, тогда:

110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.

Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

А можно воспользоваться формулой:

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Как решаем: можно найти 25% от 100:

Вычесть из исходного числа 100 − 25 = 75 человек.

Или можно воспользоваться формулой, тогда:

100 · (1 − 25 : 100) = 75/p>

Ответ: 75 выпускников в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а · (1 + у · х : 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?

Как решаем: подставим в формулу данные из условий задачи.

70 000 · (1 + 12 · 8 : 100) = 137 200

Ответ: 137 200 рублей вернет Мария через год.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?

Как решаем: просто подставим в формулу данные из условий задачи:

10000 · (1 + 10 : 100)3 = 13 310

Ответ: 13 310 рублей снимет Антон через год.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

После двух понижений изменение цены составит:

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Источник

Проектная работа «Зачем нужны проценты?». 9-й класс

Класс: 9

Автор:
Матвеева Ксения Олеговна,
9 класс

Возрастная группа: молодые исследователи.

Направление работы: естественные науки и современный мир.

Актуальность

Оглянитесь вокруг. Нас всюду окружают проценты. (Приложение 1)

Проценты» затрагивает финансовую, экономическую, демографическую и другие сферы нашей жизни. Я считаю, что умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни постоянно. Изучение процента продиктовано самой жизнью.

Приведу несколько примеров.

Когда в магазине бывают скидки, они измеряются в процентах. Стоимость товаров может снижаться, например, на 15, 20, 50%.

Также используются проценты в торговле и кулинарии (например, 9%-ный столовый уксус, сметана с жирностью 20%, 5%-ный творог, молоко 1,5% жирности).

В фармакологии, например, встречается 2%-ный раствор перекиси водорода, детские капли в нос 0,05%.

В повседневной жизни можно прочитать или услышать, например, что в выборах приняли участие 57% избирателей или успеваемость в классе 85 %; материал содержит 100% хлопка или пряжа для вязания состоит из 50% шерсти и 50 % акрила; банк начисляет 7% годовых, а рейтинг победителя хит-парада равен 75%.

Даже на дороге можно встретить знак с обозначением процентов. Так, например, этот знак обозначает подъем дороги с уклоном в 12%.

Проценты связывают между собой многие точные и естественные науки, быт и производство.

Процентные вычисления можно встретить как в математике, так и в химии (при приготовлении растворов и решении задач), географии, физике.

Проценты встречаются в банковской сфере (для расчета кредитной ставки), бухгалтерских расчетах, в статистике, науке и технике.

Поэтому, я считаю, что выбранная мною тема в настоящее время очень актуальна.

Своими исследованиями я хочу доказать одноклассникам, что знание математики и правильность процентных вычислений необходимы для применения их в дальнейшей жизни.

Цель проекта: Выяснить, где и как проценты применяются в нашей жизни. Расширить знания о применении процентных вычислений в задачах и в разных сферах жизни человека.

Задачи проекта:

План работы над проектом

Подбор и изучение литературы из различных источников по теме «Проценты в нашей жизни»

Подбор интересных фактов, задач, связанных с применением процентов

Практическая работа.
Проведение опроса среди одноклассников с целью изучения фактов из их жизни и построения диаграмм

Систематизация изученного материала и подготовка презентации

Выступление перед одноклассниками (с целью расширения их математического кругозора)

1. История возникновения процентов

Интересна история возникновения процентов. Слово процент произошло от латинского слова «pro centum», что буквально означает «За сотню» или «Со ста». Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник за каждую сотню.

Долгое время под процентами понимали чистую прибыль или убыток на каждые сто рублей. Они применялись только в торговых и денежных сделках. От римлян проценты перешли к другим народам Европы.

В Европе в средние века расширилась торговля и, следовательно, особое внимание обращалось на умение вычислять проценты. Тогда приходилось рассчитывать не только проценты, но и проценты с процентов (сложные проценты). Часто конторы и предприятия для облегчения расчетов разрабатывали особые таблицы вычисления процентов. Эти таблицы держались в тайне, составляли коммерческий секрет фирмы. Впервые таблицы были опубликованы в 1584 году Симоном Стевином. Фламандский ученый, военный инженер Симон Стевин не был по профессии математиком, но его трудолюбие и талант позволили ему занять достойное место среди выдающихся европейских математиков. Он первым в Европе открыл десятичные дроби. Симон Стевин опубликовал таблицу для вычисления сложных процентов, которая использовалась в торгово-финансовых операциях.

Затем область их применения процентов расширилась, проценты стали встречаться в хозяйственных и финансовых расчетах, статистике, науке, технике.

В разные времена процент обозначался разными символами:

XV век

XVII век

XVIII век

Интересно происхождение символа %.

Знак «%» происходит, как полагают, от итальянского слова cento(сто), которое в процентных расчётах часто писалось сокращённо cto. Отсюда путём дальнейшего упрощения буквы t в наклонную черту произошёл современный символ для обозначения процента.

2. Типы задач на проценты

Процент – это сотая часть числа (величины) 1% = 0,01.

1) Нахождение процентов от числа.

Чтобы найти процент от числа, следует:

1. Проценты записать десятичной дробью.
2. Число умножить на эту десятичную дробь.

Задача 1: В магазине «у Севы» ликвидационная распродажа товара. Весь товар можно приобрести со скидкой 50%. Сколько будут стоить джинсы, начальная цена которых 1950 руб.? Ответ: 975 руб.

2) Нахождение числа по его процентам.

Чтобы найти число по его процентам, следует:
1. Проценты записать десятичной дробью.
2. Число разделить на эту десятичную дробь.

Задача 2. Василич израсходовал 7 метров изоленты. И у него оставалось 30% от всей длины. Сколько метров изоленты было у Василича изначально?

Ответ: изначально было 10 м изоленты.

3) Нахождение процентного отношения чисел.

Чтобы узнать, сколько процентов одно число составляет от второго, следует:
1. Первое число разделить на второе.
2. Результат умножить на 100%.

Задача 3: Завод должен был за месяц изготовить 1 200 изделий, а изготовил 2 300 изделий. На сколько процентов завод перевыполнил план?

1 200 изделий — это план завода, или 100% плана.
1) Сколько изделий изготовил завод сверх плана?
2 300 — 1 200 = 1 100 (изд.)
2) Сколько процентов от плана составят сверхплановые изделия?
1 100 от 1 200 значит, 1 100 : 1 200 * 100 = 91,7 (%).

Увеличение на р%

Чтобы увеличить положительное число а на р%, следует: умножить число а на коэффициент увеличения к = (1+0,01р) а₁=а (1+0,01р)

Задача 4: Цена на яблоки выросла на 30%. Какова цена яблок после повышения, если первоначальная цена 60 рублей?

к = 1 + 0,01 ·30 = 1,3
60 · 1,3 = 78 рублей

Уменьшение на р%

Чтобы уменьшить положительное число а на р%, следует:

умножить число а на коэффициент уменьшения к = (1- 0,01·р)

Задача 5: Цена на путевку в санаторий снизилась на 10%. Сколько стоит путевка, если ее первоначальная цена 18 000 рублей?

Решение: к = 1 – 0,01·10 = 0,9; 18000 · 0,9 = 16200 рублей

Ответ: 16 200 рублей.

3. Разные сферы жизни человека в задачах на проценты

3.1 В экономической сфере

Задача 6. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?

Стоимость поездки составляет:

4∙198 + 12 ∙ (1 – 0,5) ∙ 198 = 10 ∙ 198 = 1980 рублей

Задача 7. Какая сумма (в рублях) будет проставлена в кассовом чеке, если стоимость товара 520 р., и покупатель оплачивает его по дисконтной карте с 5%-ной скидкой?

Таким образом, итоговая цена со скидкой равна: 520–26= 494 рубля.

Задача 8. Поступивший в продажу в апреле мобильный телефон стоил 4000 рублей. В сентябре он стал стоить 2560 рублей. На сколько процентов снизилась цена на мобильный телефон в период с апреля по сентябрь?

Цену на телефон снизили на 4000 − 2560 = 1440 рублей. Разделим 1440 на 4000: 1440 : 4000 = 0,36.

Значит, цену снизили на 36%.

Задача 9. Туристическая фирма организует трехдневные автобусные экскурсии. Стоимость экскурсии для одного человека составляет 3500 р. Группам предоставляются скидки: группе от 3 до 10 человек — 5%, группе более 10 человек — 10%. Сколько заплатит за экскурсию группа из 8 человек?

Стоимость экскурсии для 8 человек без учёта скидки составляет 3500 · 8 = 28 000 руб. Группе состоящей из 8 человек предоставляется скидка 5%: 28 000 · 0,05 = 1400 руб. Таким образом стоимость экскурсии составит 28 000 − 1400 = 26 600 рублей

Ответ: 26 600 рублей

Задача 10. Государству принадлежит 60% акций предприятия, остальные акции принадлежат частным лицам. Общая прибыль предприятия после уплаты налогов за год составила 40 млн. р. Какая сумма в рублях из этой прибыли должна пойти на выплату частным акционерам?

Один процент от 40 млн равен: 40 000 000 : 100 = 400 000 рублей

На выплату частным акционерам пошло: 40 000 000 ∙ 40 = 16 000 000 рублей

Ответ: 16 000 000 рублей

Задача 11. На предприятии работало 240 сотрудников. После модернизации производства их число сократилось до 192. На сколько процентов сократилось число сотрудников предприятия?

Количество сотрудников после модернизации сократилось на 240 − 192 = 48 человек.

Значит, число сотрудников сократилось на % (48 : 240) ∙100 = 20 %

3.2. В демографической сфере

Задача 12: В 2002 г. в нашем посёлке Ревда было 10 368 жителей, а в 2016 г. их стало 7822 жителя. На сколько процентов уменьшилось число жителей поселка?

Количество жителей уменьшилось на 10368 – 7822 = 2546 (чел). Значит, число жителей уменьшилось на 2546/10368 ∙ 100 = 24,55 %

3.3. В финансовой сфере

Задача 13: Городской бюджет составляет 45 млн. р., а расходы на одну из его статей составили 12,5%. Сколько рублей потрачено на эту статью бюджета?

45000000 ∙ (12,5 : 100) = 45000000 ∙ 0,125 = 5 625 000 рублей

Ответ: 5625000 рублей.

3.4. В химии: Задачи на смеси и сплавы

Задача 18: Имеется кусок сплава меди с оловом общей массой 12 кг, содержащей 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?

12 ∙ 0,45 = 5,4 (кг) меди в первом сплаве
5,4 кг – 40%
12 + x кг – 100%
12 + x = (5,4 ∙ 1000) : 40%
12 + x = 13,5
x = 13,5 – 12 = 1,5 кг

Задача 19. Сколько воды надо добавить к 0,6 литрам воды, которая содержит 40% поваренной соли, чтобы получить раствор этой соли?

0,6 ∙ 0,4 = 0,24 л
0,24 л – 12%
x л – 100%
x = (0,24 ∙ 100) : 12 = 2 л
2 –0,6 = 1,4 л

3.5. В биологии

Задача 20. Виноград содержит 75% воды, а полученный из него изюм содержит воды. Сколько изюма получится из 320 кг винограда?

Поскольку в свежем винограде 75% воды, то его масса без воды (масса сухого вещества) составляет 100 – 75 = 25% = 0,25
320 ∙ 0,25 = 80 кг (сухого вещества)

Поскольку в изюме 20% составляет вода, то эта же масса 80 кг без воды составляет 100% – 20% 80% = 0,8

4. Проценты в наглядном представлении информации

4.1 А вот, что я узнала от родителей

Так выглядит примерное распределение семейного бюджета среднестатистической семьи при доходе 46 400 рублей из 3-х человек на месяц (на конец 2018 года):

Источник