Для чего определяется доверительный интервал

Способы расчета доверительного интервала

Часто оценщику приходится анализировать рынок недвижимости того сегмента, в котором располагается объект оценки. Если рынок развит, проанализировать всю совокупность представленных объектов бывает сложно, поэтому для анализа используется выборка объектов. Не всегда эта выборка получается однородной, иногда требуется очистить ее от экстремумов – слишком высоких или слишком низких предложений рынка. Для этой цели применяется доверительный интервал. Цель данного исследования – провести сравнительный анализ двух способов расчета доверительного интервала и выбрать оптимальный вариант расчета при работе с разными выборками в системе estimatica.pro.

Способы расчета доверительного интервала

Доверительный интервал – вычисленный на основе выборки интервал значений признака, который с известной вероятностью содержит оцениваемый параметр генеральной совокупности.

Смысл вычисления доверительного интервала заключается в построении по данным выборки такого интервала, чтобы можно было утверждать с заданной вероятностью, что значение оцениваемого параметра находится в этом интервале. Другими словами, доверительный интервал с определенной вероятностью содержит неизвестное значение оцениваемой величины. Чем шире интервал, тем выше неточность.

Существуют разные методы определения доверительного интервала. В этой статье рассмотрим 2 способа:

Этапы сравнительного анализа разных способов расчета ДИ:

1. формируем выборку данных;

2. обрабатываем ее статистическими методами: рассчитываем среднее значение, медиану, дисперсию и т.д.;

3. рассчитываем доверительный интервал двумя способами;

4. анализируем очищенные выборки и полученные доверительные интервалы.

Этап 1. Выборка данных

Выборка сформирована с помощью системы estimatica.pro. В выборку вошло 91 предложение о продаже 1 комнатных квартир в 3-ем ценовом поясе с типом планировки «Хрущевка».

Таблица 1. Исходная выборка

Источник

Доверительные интервалы

Определение

Доверительные интервалы (англ. Confidence Intervals) одним из типов интервальных оценок используемых в статистике, которые рассчитываются для заданного уровня значимости. Они позволяют сделать утверждение, что истинное значение неизвестного статистического параметра генеральной совокупности находится в полученном диапазоне значений с вероятностью, которая задана выбранным уровнем статистической значимости.

Нормальное распределение

Когда известна вариация (σ 2 ) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.

Формула

Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула

где X – математическое ожидание выборки, α – уровень статистической значимости, Z_α/2 – Z-оценка для уровня статистической значимости α/2, σ – среднеквадратическое отклонение генеральной совокупности, n – количество наблюдений в выборке. При этом, σ/√ n является стандартной ошибкой.

Таким образом, доверительный интервал для уровня статистической значимости α можно записать в виде

Пример

Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Z_α/2=1,96. В этом случае нижняя и верхняя граница доверительного интервала составят

А сам доверительный интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.

Методы сужения доверительного интервала

Допустим, что диапазон [11,864; 18,136] является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.

Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Z_α/2=1,64. В этом случае нижняя и верхняя граница интервала составят

А сам доверительный интервал может быть записан в виде

В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон [12,376; 17,624].

Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов

Сам доверительный интервал станет иметь следующий вид

Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.

Построение доверительного интервала при распределении отличном от нормального

В случае если среднеквадратичное отклонение генеральной совокупности не известно или распределение отлично от нормального, для построения доверительного интервала используется t-распределение. Это методика является более консервативной, что выражается в более широких доверительных интервалах, по сравнению с методикой, базирующейся на Z-оценке.

Формула

Для расчета нижнего и верхнего предела доверительного интервала на основании t-распределения применяются следующие формулы

где X – математическое ожидание выборки, α – уровень статистической значимости, t_α – t-критерий Стьюдента для уровня статистической значимости α и количества степеней свободы (n-1), σ – среднеквадратическое отклонение выборки, n – количество наблюдений в выборке.

Сам доверительный интервал может быть записан в следующем виде

Распределение Стьюдента или t-распределение зависит только от одного параметра – количества степеней свободы, которое равно количеству индивидуальных значений признака (количество наблюдений в выборке). Значение t-критерия Стьюдента для заданного количества степеней свободы (n) и уровня статистической значимости α можно узнать из справочных таблиц.

Пример

Предположим, что размер выборки составляет 25 индивидуальных значений, математическое ожидание выборки равно 50, а среднеквадратическое отклонение выборки равно 28. Необходимо построить доверительный интервал для уровня статистической значимости α=5%.

В нашем случае количество степеней свободы равно 24 (25-1), следовательно соответствующее табличное значение t-критерия Стьюдента для уровня статистической значимости α=5% составляет 2,064. Следовательно, нижняя и верхняя граница доверительного интервала составят

А сам интервал может быть записан в виде

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [38,442; 61,558].

Использование t-распределения позволяет сузить доверительный интервал либо за счет снижения статистической значимости, либо за счет увеличения размера выборки.

Снизив статистическую значимость с 95% до 90% в условиях нашего примера мы получим соответствующее табличное значение t-критерия Стьюдента 1,711.

В этом случае мы можем утверждать, что с вероятностью 90% математическое ожидание генеральной совокупности окажется в диапазоне [40,418; 59,582].

Если мы не хотим снижать статистическую значимость, то единственной альтернативой будет увеличение объема выборки. Допустим, что он составляет 64 индивидуальных наблюдения, а не 25 как в первоначальном условии примера. Табличное значение t-критерия Стьюдента для 63 степеней свободы (64-1) и уровня статистической значимости α=5% составляет 1,998.

Это дает нам возможность утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности окажется в диапазоне [43,007; 56,993].

Выборки большого объема

К выборкам большого объема относятся выборки из генеральной совокупности данных, количество индивидуальных наблюдений в которых превышает 100. Статистические исследования показали, что выборки большего объема имеют тенденцию быть нормально распределенными, даже если распределение генеральной совокупности отличается от нормального. Кроме того, для таких выборок применение z-оценки и t-распределения дают примерно одинаковые результаты при построении доверительных интервалов. Таким образом, для выборок большого объема допускается применение z-оценки для нормального распределения вместо t-распределения.

Подведем итоги

В таблице собраны рекомендации по выбору методики построения доверительных интервалов для различных ситуаций.

Источник

Доверительные интервалы

Общий обзор

Взяв выборку из популяции, мы получим точечную оценку интересующего нас параметра и вычислим стандартную ошибку для того, чтобы указать точность оценки.

Однако, для большинства случаев стандартная ошибка как такова не приемлема. Гораздо полезнее объединить эту меру точности с интервальной оценкой для параметра популяции.

Это можно сделать, используя знания о теоретическом распределении вероятности выборочной статистики (параметра) для того, чтобы вычислить доверительный интервал (CI – Confidence Interval, ДИ – Доверительный интервал) для параметра.

Вообще, доверительный интервал расширяет оценки в обе стороны некоторой величиной, кратной стандартной ошибке (данного параметра); два значения (доверительные границы), определяющие интервал, обычно отделяют запятой и заключают в скобки.

Доверительный интервал для среднего

Использование нормального распределения

Выборочное среднее имеет нормальное распределение, если объем выборки большой, поэтому можно применить знания о нормальном распределении при рассмотрении выборочного среднего.

В частности, 95% распределения выборочных средних находится в пределах 1,96 стандартных отклонений (SD) среднего популяции.

Когда у нас есть только одна выборка, мы называем это стандартной ошибкой среднего (SEM) и вычисляем 95% доверительного интервала для среднего следующим образом:

Если повторить этот эксперимент несколько раз, то интервал будет содержать истинное среднее популяции в 95% случаев.

Обычно это доверительный интервал как, например, интервал значений, в пределах которого с доверительной вероятностью 95% находится истинное среднее популяции (генеральное среднее).

Хотя это не вполне строго (среднее в популяции есть фиксированное значение и поэтому не может иметь вероятность, отнесённую к нему) таким образом интерпретировать доверительный интервал, но концептуально это удобнее для понимания.

Использование t-распределения

Можно использовать нормальное распределение, если знать значение дисперсии в популяции. Кроме того, когда объем выборки небольшой, выборочное среднее отвечает нормальному распределению, если данные, лежащие в основе популяции, распределены нормально.

Если данные, лежащие в основе популяции, распределены ненормально и/или неизвестна генеральная дисперсия (дисперсия в популяции), выборочное среднее подчиняется t-распределению Стьюдента.

Вычисляем 95% доверительный интервал для генерального среднего в популяции следующим образом:

где — процентная точка (процентиль) t-распределения Стьюдента с (n-1) степенями свободы, которая даёт двухстороннюю вероятность 0,05.

Вообще, она обеспечивает более широкий интервал, чем при использовании нормального распределения, поскольку учитывает дополнительную неопределенность, которую вводят, оценивая стандартное отклонение популяции и/или из-за небольшого объёма выборки.

Когда объём выборки большой (порядка 100 и более), разница между двумя распределениями (t-Стьюдента и нормальным) незначительна. Тем не менее всегда используют t-распределение при вычислении доверительных интервалов, даже если объем выборки большой.

Обычно указывают 95% ДИ. Можно вычислить другие доверительные интервалы, например 99% ДИ для среднего.

Вместо произведения стандартной ошибки и табличного значения t-распределения, которое соответствует двусторонней вероятности 0,05, умножают её (стандартную ошибку) на значение, которое соответствует двусторонней вероятности 0,01. Это более широкий доверительный интервал, чем в случае 95%, поскольку он отражает увеличенное доверие к тому, что интервал действительно включает среднее популяции.

Доверительный интервал для пропорции

Выборочное распределение пропорций имеет биномиальное распределение. Однако если объём выборки n разумно большой, тогда выборочное распределение пропорции приблизительно нормально со средним .

Оцениваем выборочным отношением p=r/n (где r– количество индивидуумов в выборке с интересующими нас характерными особенностями), и стандартная ошибка оценивается:

95% доверительный интервал для пропорции оценивается:

Если объём выборки небольшой (обычно когда np или n(1-p) меньше 5), тогда необходимо использовать биномиальное распределение для того, чтобы вычислить точные доверительные интервалы.

Заметьте, что если p выражается в процентах, то (1-p) заменяют на (100-p).

Интерпретация доверительных интервалов

При интерпретации доверительного интервала нас интересуют следующие вопросы:

Насколько широк доверительный интервал?

Широкий доверительный интервал указывает на то, что оценка неточна; узкий указывает на точную оценку.

Ширина доверительного интервала зависит от размера стандартной ошибки, которая, в свою очередь, зависит от объёма выборки и при рассмотрении числовой переменной от изменчивости данных дают более широкие доверительные интервалы, чем исследования многочисленного набора данных немногих переменных.

Включает ли ДИ какие-либо значения, представляющие особенный интерес?

Можно проверить, ложится ли вероятное значение для параметра популяции в пределы доверительного интервала. Если да, то результаты согласуются с этим вероятным значением. Если нет, тогда маловероятно (для 95% доверительного интервала шанс почти 5%), что параметр имеет это значение.

Источник

Доверительный интервал

Опубликовано 15.06.2021 · Обновлено 16.06.2021

Что такое Доверительный интервал?

Ключевые моменты

Понимание доверительного интервала

Статистики используют доверительные интервалы для измерения неопределенности переменной выборки. Например, исследователь случайным образом выбирает разные образцы из одной и той же совокупности и вычисляет доверительный интервал для каждой выборки, чтобы увидеть, как она может представлять истинное значение переменной совокупности. Все полученные наборы данных разные; некоторые интервалы включают параметр истинной популяции, а другие нет.

Краткая справка

Доверительный интервал и доверительный уровень взаимосвязаны, но не одно и то же.

Расчет доверительного интервала

Предположим, группа исследователей изучает рост баскетболистов средней школы. Исследователи выбирают случайную выборку из населения и устанавливают средний рост в 74 дюйма.

Среднее значение в 74 дюйма – это точечная оценка среднего значения для населения. Точечная оценка сама по себе имеет ограниченную полезность, потому что она не выявляет неопределенности, связанной с оценкой; у вас нет четкого представления о том, насколько далеко это среднее значение выборки в 74 дюйма может быть от среднего значения генеральной совокупности. Чего не хватает, так это степени неопределенности в этом единственном образце.

Доверительные интервалы предоставляют больше информации, чем точечные оценки. Установив 95% доверительный интервал с использованием среднего и стандартного отклонения по выборке и предположив нормальное распределение, представленное колоколообразной кривой, исследователи пришли к верхней и нижней границе, которая содержит истинное среднее значение в 95% случаев.

Предположим, что интервал составляет от 72 до 76 дюймов. Если исследователи возьмут 100 случайных выборок из популяции баскетболистов средней школы в целом, среднее значение должно быть от 72 до 76 дюймов в 95 из этих выборок.

Примеры доверительного интервала

Если исследователи хотят еще большей уверенности, они могут расширить интервал до 99% уверенности. Это неизменно приводит к более широкому диапазону, поскольку освобождает место для большего числа выборочных средних. Если они установят 99% доверительный интервал как от 70 до 78 дюймов, они могут ожидать, что 99 из 100 оцененных образцов будут содержать среднее значение между этими числами.

С другой стороны, уровень достоверности 90% означает, что мы ожидаем, что 90% интервальных оценок будут включать параметр генеральной совокупности и т. Д.

Особые соображения

Самое большое заблуждение относительно доверительных интервалов заключается в том, что они представляют собой процент данных из данной выборки, который попадает между верхней и нижней границами.

Источник

Доверительный интервал. Азбука медицинской статистики. Глава III

Константин Кравчик доходчиво объясняет, что такое доверительный интервал в медицинских исследованиях и как его использовать

«Катрен-Стиль» продолжает публикацию цикла Константина Кравчика о медицинской статистике. В двух предыдущих статьях автор касался объяснения таких понятий, как размер выборки, генеральная совокупность, статистическая гипотеза и классификацию шкал.

Математик-аналитик. Специалист в области статистических исследований в медицине и гуманитарных науках

Очень часто в статьях по клиническим исследованиям можно встретить загадочное словосочетание: «доверительный интервал» (95 % ДИ или 95 % CI — confidence interval). Например, в статье может быть написано: «Для оценки значимости различий использовали t-критерий Стьюдента с расчетом 95 % доверительного интервала».

Какого же значение «95 % доверительного интервала» и зачем его рассчитывать?

Что такое доверительный интервал? — Это диапазон, в котором находятся истинные средние значения в генеральной совокупности. А что, бывают «неистинные» средние значения? В каком‑то смысле да, бывают. В прошлой статье мы объясняли, что невозможно измерить интересующий параметр во всей генеральной совокупности, поэтому исследователи довольствуются ограниченной выборкой. В этой выборке (например, по массе тела) есть одно среднее значение (определенный вес), по которому мы и судим о среднем значении во всей генеральной совокупности. Однако едва ли средний вес в выборке (особенно небольшой) совпадет со средним весом в генеральной совокупности. Поэтому более правильно рассчитывать и пользоваться диапазоном средних значений генеральной совокупности.

Например, представим, что 95 % доверительный интервал (95 % ДИ) по гемоглобину составляет от 110 до 122 г/л. Это означает, что с вероятностью 95 % истинное среднее значение по гемоглобину в генеральной совокупности будет находиться в пределах от 110 до 122 г/л. Иными словами, мы не знаем средний показатель гемоглобина в генеральной совокупности, но можем с 95 %-й вероятностью указать диапазон значений для этого признака.

Доверительный интервал особенно уместен для разницы в средних значениях между группами или, как это называют, в размере эффекта.

Допустим, мы сравнивали эффективность двух препаратов железа: давно присутствующего на рынке и только что зарегистрированного. После курса терапии оценили концентрацию гемоглобина в исследуемых группах пациентов, и статистическая программа нам посчитала, что разность между средними значениями двух групп с вероятностью 95 % находится в диапазоне от 1,72 до 14,36 г/л (табл. 1).

Табл. 1. Критерий для независимых выборок
(сравниваются группы по уровню гемоглобина)

Трактовать это следует так: у части пациентов генеральной совокупности, которая принимает новый препарат, гемоглобин будет выше в среднем на 1,72–14,36 г/л, чем у тех, кто принимал уже известный препарат.

Иными словами, в генеральной совокупности разность в средних значениях по гемоглобину у групп с 95 %-й вероятностью находится в этих пределах. Судить, много это или мало, будет уже исследователь. Смысл всего этого в том, что мы работаем не с одним средним значением, а с диапазоном значений, следовательно, мы более достоверно оцениваем разницу по параметру между группами.

В статистических пакетах, на усмотрение исследователя, можно самостоятельно сужать или расширять границы доверительного интервала. Снижая вероятности доверительного интервала, мы сужаем диапазон средних. Например, при 90 % ДИ диапазон средних (или разницы средних) будет уже, чем при 95 %.

И наоборот, увеличение вероятности до 99 % расширяет диапазон значений. При сравнении групп нижняя граница ДИ может пересечь нулевую отметку. Например, если мы расширили границы доверительного интервала до 99 %, то границы интервала расположились от –1 до 16 г/л. Это означает, что в генеральной совокупности есть группы, различие средних между которыми по изучаемому признаку равняется 0 (М=0).

Почему рекомендуется смотреть на доверительный интервал? Для большей наглядности обратимся к рисунку.

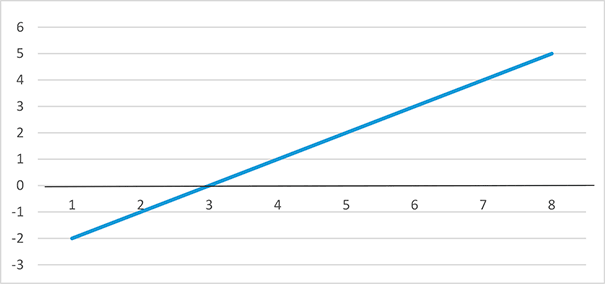
95% доверительный интервал разницы по гемоглобину, (г/л)

На рисунке в виде линии изображен 95 % доверительный интервал разницы средних значений по гемоглобину между двумя группами. Линия проходит нулевую отметку, следовательно, имеет место разница между средними значениями, равная нулю, что подтверждает нулевую гипотезу о том, что группы не различаются. Диапазон разницы между группами лежит от –2 до 5 г/л, Это означает, что гемоглобин может как снизиться на 2 г/л, так и повыситься на 5 г/л.

Доверительный интервал — очень важный показатель. Благодаря ему можно посмотреть, были ли различия в группах действительно за счет разности средних или за счет большой выборки, т. к. при большой выборке шансы найти различия больше, чем при малой.

На практике это может выглядеть так. Мы взяли выборку в 1000 человек, измерили уровень гемоглобина и обнаружили, что доверительный интервал разницы средних лежит от 1,2 до 1,5 г/л. Уровень статистической значимости при этом p 23062 просмотров

Нашли ошибку? Выделите текст и нажмите Ctrl+Enter.

Источник