Для чего применяется теорема штейнера
Теорема Штейнера или теорема параллельных осей для вычисления момента инерции
При математическом описании вращательного движения важно знать момент инерции системы относительно оси. В общем случае процедура нахождения этой величины предполагает реализацию процесса интегрирования. Облегчить вычисления позволяет так называемая теорема Штейнера. Рассмотрим ее подробнее в статье.
Что такое момент инерции?
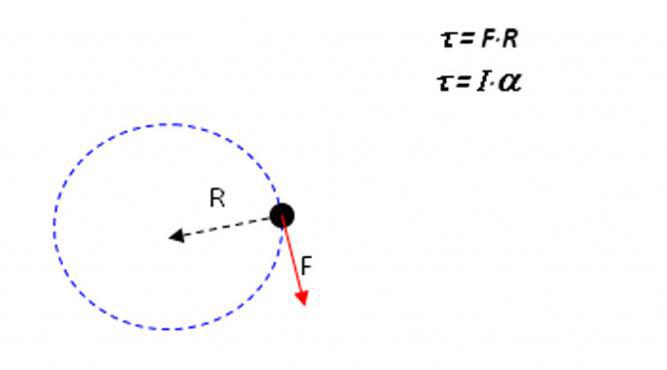
До того как привести формулировку теоремы Штейнера, следует разобраться с самим понятием момента инерции. Допустим, имеется некоторое тело определенной массы и произвольной формы. Этим телом может быть, как материальная точка, так и любой двумерный и трехмерный объект (стержень, цилиндр, шар и т.д.). Если рассматриваемый объект совершает круговое движение вокруг некоторой оси с постоянным угловым ускорением α, тогда можно записать следующее уравнение:

Момент инерции и теорема Штейнера
Известный швейцарский математик, Якоб Штейнер, доказал теорему о параллельных осях и моменте инерции, которая теперь носит его фамилию. Эта теорема постулирует, что момент инерции для абсолютно любого твердого тела произвольной геометрии относительно некоторой оси вращения равен сумме момента инерции относительно оси, которая пересекает центр масс тела и параллельна первой, и произведения массы тела на квадрат дистанции между этими осями. Математически эта формулировка записывается так:
Теорема позволяет, зная величину IO, рассчитать любой другой момент IZ относительно оси, которая параллельна O.
Доказательство теоремы
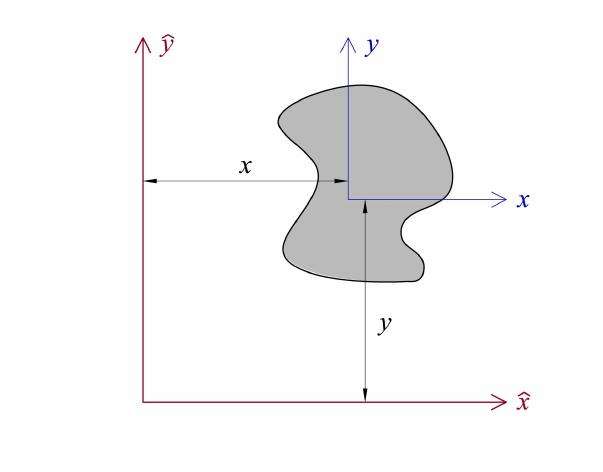
Формулу теоремы Штейнера можно легко получить самостоятельно. Для этого рассмотрим произвольное тело на плоскости xy. Пусть начало координат проходит через центр масс этого тела. Рассчитаем момент инерции IO которая проходит через начало координат перпендикулярно плоскости xy. Поскольку расстояние до любой точки тела выражается формулой r = √ (x2 + y2), тогда получаем интеграл:
IO = ∫m (r2*dm) = ∫m ( (x2+y2) *dm)
Теперь переместим параллельно ось вдоль оси x на расстояние l, например, в положительном направлении, тогда расчет для новой оси момента инерции будет выглядеть следующим образом:
Раскроем полный квадрат в скобках и разделим подынтегральные суммы, получим:
IZ = ∫m ( (x2+l2+2*x*l+y2)*dm) = ∫m ( (x2+y2)*dm) + 2*l*∫m (x*dm) + l2*∫mdm
Первое из этих слагаемых является величиной IO, третье слагаемое, после проведения интегрирования, дает член l2*m, а вот второе слагаемое равно нулю. Обнуление указанного интеграла связано с тем, что он берется от произведения иксов на элементы массы dm, что в среднем дает ноль, так как центр масс находится в начале координат. В итоге, получается формула теоремы Штейнера.
Рассмотренный случай на плоскости можно обобщить на объемное тело.
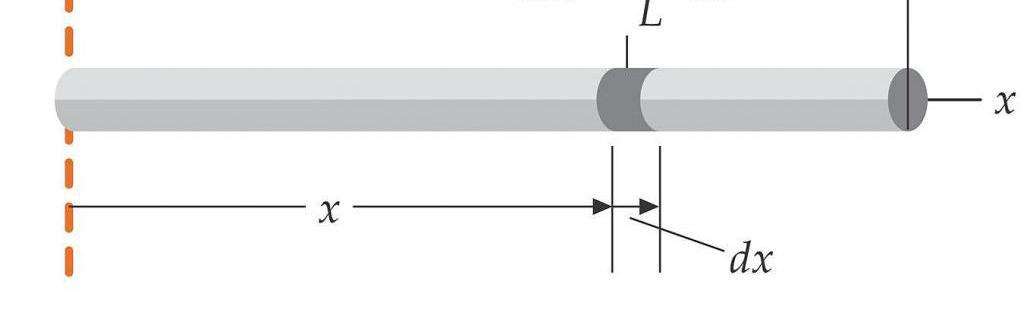
Проверка формулы Штейнера на примере стержня
Приведем простой пример, на котором продемонстрируем, как пользоваться рассмотренной теоремой.
Известно, что для стержня длиной L и массой m момент инерции IO (ось проходит через центр масс) равен m*L2/12, а момент IZ (ось проходит через конец стержня) равен m*L2/3. Проверим эти данные, воспользовавшись теоремой Штейнера. Поскольку расстояние между двумя осями равно L/2, тогда получаем момент IZ:
IZ = IO + m*(L/2)2 = m*L2/12 + m*L2/4 = 4*m*L2/12 = m*L2/3
То есть мы проверили формулу Штейнера и получили такое же значение для IZ, что и в источнике.
Аналогичные вычисления можно проводить и для других тел (цилиндра, шара, диска), получая при этом необходимые моменты инерции, и не производя интегрирования.
Момент инерции и перпендикулярные оси
Рассмотренная теорема касается параллельных осей. Для полноты информации полезно также привести теорему для перпендикулярных осей. Она формулируется так: для плоского объекта произвольной формы момент инерции относительно перпендикулярной ему оси будет равен сумме двух моментов инерции относительно двух взаимно перпендикулярных и лежащих в плоскости объекта осей, при этом все три оси должны проходить через одну точку. Математически это записывается так:
Существенное отличие этой теоремы от теоремы Штейнера заключается в том, что она применима только к плоским (двумерным) твердым объектам. Тем не менее на практике ее достаточно широко используют, мысленно разрезая тело на отдельные слои, а затем, складывая полученные моменты инерции.
Момент инерции для чайников: определение, формулы, примеры решения задач
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Теорема Штейнера: объяснение, приложения, упражнения
Содержание:
В Теорема Штейнера, также известный как теорема о параллельных осях, позволяет оценить момент инерции вытянутого тела вокруг оси, параллельной другой оси, проходящей через центр масс объекта.
Он был открыт швейцарским математиком Якобом Штайнером (1796–1863) и утверждает следующее: пусть яСМ момент инерции объекта относительно оси, проходящей через его центр масс CM и Iz момент инерции относительно другой параллельной ей оси.
Зная расстояние D, разделяющее обе оси, и массу M рассматриваемого тела, момент инерции относительно неизвестной оси равен:
Приложения
Поскольку объект способен вращаться вокруг множества осей, а в таблицах обычно указывается только момент инерции относительно оси, проходящей через центроид, теорема Штейнера упрощает расчет, когда необходимо вращать тела по осям. которые не соответствуют этому.
Например, дверь обычно вращается не вокруг оси, проходящей через ее центр масс, а вокруг боковой оси, к которой примыкают петли.
Зная момент инерции, можно вычислить кинетическую энергию, связанную с вращением вокруг указанной оси. да K кинетическая энергия, я момент инерции вокруг рассматриваемой оси и ω угловой скорости, выполняется следующее:
Доказательство теоремы Штейнера
Момент инерции протяженного объекта определяется как:
кудадм бесконечно малая часть массы и р это расстояние между дм и ось вращения z. На рисунке 2 эта ось проходит через центр масс CM, но он может быть любым.
Вокруг другой осиz ’, момент инерции равен:
Теперь согласно треугольнику, образованному векторами D, р Y р ‘ (см. рисунок 2 справа) есть векторная сумма:
р + р ‘ = D → р ‘ = D – р
Три вектора лежат в плоскости объекта, который может бытьху. Начало системы координат (0,0) выбирается в CM, чтобы облегчить последующие вычисления.
Таким образом, квадрат модуля вектора р ‘ это:
Теперь эта развертка подставляется в интеграл момента инерции Izа также используется определение плотности dm = ρ.dV:
С другой стороны, третий и четвертый интегралы имеют значение 0, так как по определению они составляют позицию CM, которая была выбрана в качестве начала системы координат (0,0).
Решенные упражнения
-Решенное упражнение 1
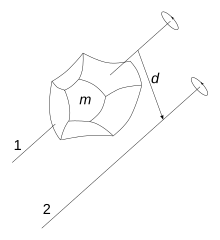
Прямоугольная дверь на рисунке 1 имеет массу 23 кг, ширину 1,30 и высоту 2,10 м. Определите момент инерции двери по отношению к оси, проходящей через петли, при условии, что дверь тонкая и однородная.
Решение
Из таблицы моментов инерции для прямоугольной пластины массы M и размеров к Y б, момент инерции относительно оси, проходящей через его центр масс, равен: IСМ = (1/ 12)M(к 2 + б 2 ).
Предполагается однородный вентиль (приблизительное значение, поскольку вентиль на рисунке, вероятно, не является таким). В таком случае центр масс проходит через его геометрический центр. На рисунке 3 проведена ось, проходящая через центр масс и параллельная оси, проходящей через шарниры.
яСМ = (1/12) x 23 кг x (1,30 2 +2.10 2 ) м 2 = 11,7 кг / м 2
Применяя теорему Штейнера для зеленой оси вращения:
Я = ЯСМ + MD 2 = 11,7 кг / м 2 + 23 кг x 0,652 м 2 = 21,4 кг.
-Решенное упражнение 2
Найдите момент инерции однородного тонкого стержня при его вращении вокруг оси, проходящей через один из его концов, см. Рисунок. Он больше или меньше момента инерции при вращении вокруг своего центра? Зачем?
Решение
Согласно таблице моментов инерции момент инерции яСМ тонкого тестового прутка M и длина L это:яСМ = (1/12) мл 2
И теорема Штейнера утверждает, что когда он вращается вокруг оси, проходящей через один конец D = L / 2, он остается:
Я = ЯСМ + MD 2 = (1/12) мл 2 + M (L / 2) 2 = (1/3) мл 2
Он больше, но не просто вдвое, а в 4 раза больше, так как другая половина стержня (не заштрихованная на рисунке) вращается, описывая больший радиус.
Ссылки
Нормальность (химия): из чего состоит и примеры
Дерматиломания: характеристики, данные и методы лечения
Теорема Штейнера
Теорема также используются для определения геометрических моментов по инерции из пучка поперечных сечений.
Оглавление
Приложение к моментам инерции
При применении теоремы Штейнера необходимо соблюдать две вещи:
Приложение к геометрическим моментам инерции
Если центр тяжести поперечного сечения тела не находится в начале системы координат, момент инерции его площади можно вычислить с помощью теоремы Штейнера:
J у ¯ у ¯ знак равно J у у + z ¯ С. 2 ⋅ А. <\ displaystyle J _ <<\ bar ^ <2>\ cdot A> 
^ <2>\ cdot A> 
\ cdot <\ bar \ cdot A>
Эти формулы можно использовать для разделения сложных (например, тавровых балок ) на простые тела (например, прямоугольники), момент инерции которых уже известен.
В этом случае применяется, например, следующее: J у <\ displaystyle J_
Обобщение на тензоры инерции
Поэтому также применяется
В результате сдвига может случиться так, что оси новой системы координат больше не совпадают с главными осями инерции из-за новой точки.
Вывод
Расширение списков в скобках
Теорема Штейнера
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
Док-во теоремы Штейнера
Поместим начало координат в центр инерции,
т.е.
Из определения ц.инерции следует:
Описание слайда:
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
ВЫСОКОЧАСТОТНЫЕ ЭЛЕКТРИЧЕСКИЕ ПОЛЯ И ТОКИ
ПОКАЗАТЕЛИ ЭФФЕКТИВНОСТИ ИСПОЛЬЗОВАНИЯ МАТЕРИАЛЬНЫХ РЕСУРСОВ
Job interview
ПРОБЛЕМА И МЕТОДЫ ЕЕ РЕШЕНИЯ
8 ways of SUCCESS
Електромагнітні коливання
Warehousing
Кровь и лимфа
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5340776 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Комиссия РАН призвала отозвать проект новых правил русского языка
Время чтения: 2 минуты
Минпросвещения предлагает закрыть пляжи детских лагерей для посторонних лиц
Время чтения: 1 минута
В России отцы охотнее дают деньги детям на карманные расходы, чем матери
Время чтения: 2 минуты
В Псковской области ввели обязательную вакцинацию для студентов
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.