Для чего служит тоннелирование дуг
Квантовое туннелирование элементарных частиц и сверхсветовые перемещения
Экспериментально подтверждается, что элементарная частица должна превысить скорость света, если квантовомеханическим образом «туннелирует» через стену.
Едва только были открыты радикальные уравнения квантовой механики, физики обнаружили один из страннейших феноменов, допускаемых этой теорией.
«Квантовое туннелирование» демонстрирует, сколь глубоко отличаются элементарные частицы, например, электроны, от макроскопических объектов. Например, бросьте мяч о стену – и он отскочит. Дайте ему скатиться на дно ложбинки, и он останется там. Но частица в первом случае может случайно проскочить сквозь стену. У частицы есть шанс «проскользнуть через гору и выкатиться из ложбинки», как написали в журнале Nature двое физиков в 1928 году, в одной из самых ранних характеристик квантового туннелирования.
Физики быстро обнаружили, что способность частиц туннелировать сквозь барьеры позволяет разрешить многие тайны. Эта способность объясняет и различные химические связи, и радиоактивный распад, и термоядерный синтез в недрах Солнца, где ядрам водорода удается преодолеть взаимное отталкивание и слиться – в результате чего возникает солнечный свет.
Но физиков одолело любопытство, сначала умеренное, а потом по-настоящему болезненное. Сколько же времени требуется частице, чтобы туннелировать сквозь барьер?
Проблема заключалась в том, что ответ получался бессмысленным.
Только в 1962 году инженер Томас Хартман из «Texas Instruments» написал статью, в которой открыто принимал шокирующие выводы, проистекавшие из математики.
Хартман обнаружил, что по принципу действия барьер напоминает короткое замыкание. Когда частица туннелирует, она тратит на перемещение меньше времени, чем если бы барьер отсутствовал. Еще поразительнее оказалось вот что: он рассчитал, что при утолщении барьера практически не увеличивается время, нужное частице, чтобы через него туннелировать. Таким образом, при наличии достаточно толстого барьера частица могла бы перескочить с одной его стороны на другую быстрее, чем свет преодолел бы то же расстояние в вакууме.
Короче говоря, квантовое туннелирование открывает возможность для сверхсветовых перемещений, которые, казалось бы, в физике не допускаются.
“Настоящие поводы для беспокойства появились только после открытия эффекта Хартмана,” – сказал Стейнберг.
Эта дискуссия закручивалась десятилетиями, отчасти потому, что вопрос о времени туннелирования затрагивает один из наиболее загадочных аспектов квантовой механики. «Отчасти он касается общей проблемы, которая позволила бы понять, что такое время, и как время измеряется в квантовой механике, и что это значит,” сказал Илай Поллак, физик-теоретик из Института Вейцмана в Израиле. Со временем физики вывели не менее 10 альтернативных математических выражений, описывающих туннелирование во времени, и каждое из них отражает свой взгляд на процесс туннелирования. Ни один из этих вариантов не позволил решить проблему.
Но сегодня вопрос о том, как соотносится туннелирование и время, вновь обретает актуальность, благодаря серии виртуозных экспериментов, позволивших точно измерить время туннелирования в лаборатории.
Эфраим Стейнберг, физик из университета Торонто. Занимается проблемой времени туннелирования уже не одно десятилетие.
Измерительный опыт, получивший наиболее высокую оценку на настоящий момент, был описан в одной из публикаций в июльском номере журнала Nature. Группа Стейнберга из университета Торонто воспользовалась методом под названием «часы Лармора», чтобы оценить, как атомы рубидия туннелируют через лазерное поле, в котором действуют силы отталкивания.
“Часы Лармора – наилучший и наиболее понятный способ измерить время туннелирования, и это был первый эксперимент, в рамках которого это время удалось очень хорошо измерить,” сказал Игорь Литвинюк, физик из университета Гриффита в Австралии, описавший иную попытку такого измерения времени туннелирования и также опубликовавший статью в журнале Nature.
Луис Манзони, физик-теоретик из Конкордия-Колледж, штат Миннесота, также находит убедительными измерения с применением часов Лармора. «Они в самом деле измеряют время туннелирования,” – говорит он.
Последние эксперименты вновь привлекают внимание к нерешенной проблеме. С момента публикации статьи Хартмана минуло шесть десятилетий, и независимо от того, как тщательно физики переопределяли время туннелирования или с какой точностью измеряли его в лаборатории, неизменно обнаруживалось, что при квантовом туннелировании проявляется эффект Хартмана. Представляется, что туннелирование является неисправимо, непоколебимо сверхсветовым процессом.
Литвинюк предлагает задуматься, “как это возможно, чтобы [туннелирующая частица] двигалась быстрее света?” и отмечает, что “это была чистая теория, пока не были выполнены измерения.”
Сколько времени?
Время туннелирования сложно зафиксировать, как и понять, что такое реальность.
В макроскопических масштабах время, затрачиваемое объектом для перехода из точки A в точку B, можно узнать, просто разделив расстояние на скорость объекта. Но в квантовой теории невозможно одновременно точно знать расстояние и скорость.
В квантовой теории у частицы есть целый спектр возможных местоположений и скоростей. Определенные варианты из всех этих возможностей в момент измерения словно кристаллизуются. Как именно это происходит – один из глубочайших вопросов.
Чтобы понять эту проблему в контексте туннелирования, начертим колоколообразную кривую, соответствующую всем возможным местоположениям частицы. Такая кривая, называемая «волновым пакетом», центрирована по позиции А. Теперь изобразим перемещение волнового пакета по направлению к барьеру, он при этом будет выглядеть как цунами (или как солитон? – прим. пер.). Уравнения квантовой механики описывают, как волновой пакет раздваивается при столкновении с препятствием. Большая часть пакета отражается и направляется обратно к А. Но меньший пик вероятности проскальзывает сквозь барьер и продолжает движение к B. Следовательно, существует шанс, что детектор зарегистрирует частицу в B.
Но, когда частица прибудет в B, что можно будет сказать о ее пути, или о том, как долго она находилась в барьере? Прежде, чем она внезапно появилась B, эта частица представляла собой двухчастную вероятностную волну, одна ее часть была отражена, а вторая просочилась. Волна одновременно преодолела барьер и не преодолела. В таком случае смысл «времени туннелирования» становится неясен.
Но, все-таки, невозможно отрицать, что любая частица, которая вышла из A и оказалась в B, обязательно проходит через барьер, и в какой-то момент взаимодействует с барьером. Вопрос – в какой именно момент?
Но в случае с туннелированием никаких часов внутри частицы не установлено. Как же отслеживать изменения, происходящие с ней? Физики нашли множество «прокси» для туннелирования времени.
Туннелирование и время
Хартман (а до него Лерой Арчибальд Макколл в 1932 году) избрали простейший подход, позволяющий оценить, сколько времени уходит на туннелирование. Хартман рассчитал разницу между временем наиболее вероятного прибытия частицы из точки A в точку B в вакууме по сравнению с аналогичным временем, затрачиваемым, когда частица преодолевает барьер. Для этого он учел, как барьер сдвигает пиковую позицию на колоколообразной кривой передаваемого волнового пакета.
Но с этим подходом есть проблема, и она связана с тем престранным допущением, будто барьер ускоряет частицы. Мы попросту не можем сравнить исходный и конечный пик волнового пакета частицы. Отмеряя на часах разницу между наиболее вероятным временем отправления частицы (когда пик ее колоколообразной кривой находится в точке A) и ее наиболее вероятным временем прибытия (когда пик достигает точки B), мы не узнаем, сколько времени летела конкретная частица, поскольку частица, зафиксированная в B, не обязательно отправилась из A. На момент изначального вероятностного распределения она была везде и нигде, и могла быть, например, в переднем хвосте распределения, который расположен сравнительно близко к барьеру. В таком случае у нее будет шанс быстро достичь B.
Поскольку точные траектории частиц узнать невозможно, исследователи стали искать более вероятностный подход. Рассмотрели тот факт, что, если частица попадает в барьер, то в каждый момент времени существует некоторая вероятность, что частица находится внутри барьера (и вероятность, что она вне барьера). Затем физики суммируют вероятности для каждого мгновения и выводят среднее время туннелирования.
По поводу того, как измерять вероятности, в конце 1960-х были изобретены различные мысленные эксперименты, в которых «часы» можно прикреплять к самим частицам. Если часы каждой частицы «тикают», только пока она находится внутри барьера, и мы снимем показания с часов множества переданных частиц, то у нас получится разброс различных значений времени. Однако, среднее значение будет соответствовать времени туннелирования.
Встраиваемые часы
Хотя физики занимались оценкой времени туннелирования с 1980-х, сверхточные измерения стали быстро развиваться сравнительно недавно – в лаборатории Урсулы Келлер в Швейцарской высшей технической школе, Цюрих. Команда Урсулы Келлер смогла измерить время туннелирования при помощи так называемых атточасов. В атточасах Келлер электрон из атома гелия попадает в барьер, который вращается на месте, подобно стрелке часов. Электроны туннелируют чаще всего, когда барьер находится в определенной ориентации – допустим, по атточасам это полдень. Затем, когда электроны появляются из барьера, их отбрасывает в направлении, зависящем от положения барьера в тот момент. Чтобы оценить время туннелирования, команда Келлер измеряла угловую разницу между полуднем, на который приходилось большинство актов туннелирования, и углом, под которым улетали большинство исходящих электронов. Так удалось измерить разницу в 50 аттосекунд, то есть, миллиардных миллиардных долей секунды.
Затем, в работе, о которой было сообщено в 2019 году, группа Литвинюка смогла улучшить эксперимент Келлер с атточасами, взяв вместо гелия более простые атомы водорода. Они измерили даже более краткие промежутки времени, не более двух аттосекунд — это позволяет предположить, что туннелирование происходит почти мгновенно.
Но некоторые эксперты пришли к выводу, что атточасы – не слишком подходящий прибор для измерения времени туннелирования. Манзони, опубликовавший анализ таких измерений, указал, что этот подход ущербен в том же отношении, что и определение времени туннелирования по Хартману. Задним числом можно сказать, что у электронов, практически мгновенно туннелировавших сквозь барьер, была фора.
Тем временем Стейнберг, Рамос и их торонтские коллеги Дэвид Спирингс и Изабель Расико провели эксперимент, оказавшийся более убедительным.
Этот альтернативный подход опирается на факт, что многим частицам присуще магнитное свойство, которое называется «спин». Спин можно сравнить со стрелкой, которая может указывать только вверх или вниз. Но до измерения она может указывать куда угодно. Как открыл в 1897 году ирландский физик Джозеф Лармор, угол спина характеризуется вращением или «прецессией», когда частица находится в магнитном поле. Команда из Торонто смогла уподобить такую прецессию ходу часовых стрелок, и полученное устройство назвали «часами Лармора».
В качестве барьера исследователи воспользовались лазерным лучом и пропустили сквозь него магнитное поле. Затем подготовили атомы рубидия, чьи спины были ориентированы в определенном направлении, и дали этим атомам пройти сквозь барьер. Далее измерили спины атомов, вышедших с другой стороны. Если измерить спин отдельного атома, то всегда получаешь неинформативный результат «вверх» или «вниз». Но, если повторять измерение снова и снова, то совокупные измерения покажут, какую прецессию претерпели спины, пока атомы находились в барьере – следовательно, сколько времени они там провели.
Исследователи сообщили, что атом рубидия остается внутри барьера в среднем на протяжении 0,61 миллисекунд, что согласуется с теми показаниями часов Лармора, что были теоретически спрогнозированы в 1980-е. Чтобы проделать этот путь в вакууме, атомам потребовалось бы больше времени. Следовательно, эти расчеты показывают: если сделать достаточно толстый барьер, то такое ускорение позволит атомам туннелировать сквозь него быстрее скорости света.
Тайна, а не парадокс
Исследователи подчеркивают, что сверхсветовое туннелирование допустимо, коль скоро не допускает сверхсветовой передачи сигналов. По принципу оно похоже на «жуткое дальнодействие», изрядно беспокоившее Эйнштейна. Феномен «жуткого дальнодействия» связан с феноменом квантовой запутанности между сильно удаленными частицами, так, что акт измерения одной частицы мгновенно сказывается на состоянии обеих. Такая мгновенная связь между двумя частицами не вызывает парадоксов, поскольку с ее помощью частицы не могут обмениваться информацией друг с другом.
В статье, опубликованной в New Journal of Physics, Поллак и двое его коллег высказываются, что сверхсветовое туннелирование не допускает сверхсветового обмена сигналами по статистическим причинам: пусть даже туннелирование сквозь исключительно толстый барьер происходит очень быстро, крайне низка вероятность, что туннелирование сквозь такой барьер вообще произойдет. Поэтому адресату всегда целесообразнее отправлять сигнал в вакууме.
Почему же не послать тучи частиц сквозь очень-очень толстый барьер, надеясь, что хотя бы одна преодолеет его со сверхсветовой скорости. Не будет ли достаточно всего одной частицы, чтобы передать ваше сообщение и сломать физику? Стейнберг, согласный со статистической трактовкой такой ситуации, настаивает, что единственной туннелировавшей частицы не хватит, чтобы передать информацию. У сигнала должна быть структура и детализация, а любой детализированный сигнал быстрее дойдет до адресата в эфире, нежели через ненадежный барьер.
Поллак считает, что эти вопросы требуют дальнейшего изучения. «Я думаю, что эксперименты Стейнберга подстегнут развитие теории. Куда она нас приведет – не знаю».
Размышления будут сопровождаться новыми экспериментами, у Стейнберга их целый список. Локализуя магнитное поле в разных областях барьера, Стейнберг и его коллеги рассчитывают проверить «не только длительность времени, которое проводит частица внутри барьера, но и где именно она проводит это время». Согласно теоретическим расчетам, большую часть времени атомы рубидия проводят на входе в барьер и на выходе из него, а в середине почти не задерживаются. Рамос отмечает, что «это удивительно и совершенно не поддается объяснению».
Зондируя множество частиц и усредняя, что именно с ними происходит, исследователи все детальнее изображают, что происходит «внутри горы», о чем пионеры квантовой механики даже не могли подумать более века назад. С точки зрения Стейнберга, эти разработки подсказывают: несмотря на все странности, характерные для квантовой механики, «если знать, где в итоге оказалась частица, можно подробнее определить, что с ней происходило до этого».
Тоннелирование стрелок
Тоннелирование стрелок. Вновь внесенные граничные стрелки на диаграмме декомпозиции нижнего уровня изображаются в квадратных скобках и автоматически не появляются на диаграмме верхнего уровня «Неразрешенная (unresolved) стрелка» (рис.35).
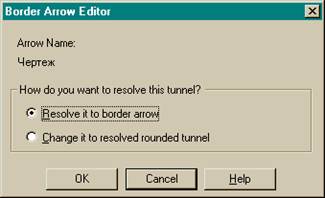
Для их «перетаскивания» наверх нужно сначала выбрать кнопку на палитре инструментов щелкнуть по квадратным скобкам граничной стрелки. Появляется диалог Border Arrow Editor. (рис. 36).
Тоннелирование может быть применено для изображения малозначимых стрелок. Если на какой-либо диаграмме нижнего уровня необходимо изобразить малозначимые данные или объекты, которые не обрабатываются или не используются работами на текущем уровне, то их необходимо направить на вышестоящий уровень (на родительскую диаграмму). Если эти данные не используются на родительской диаграмме, их нужно направить еще выше, и т.д. В результате малозначимая стрелка будет изображена на всех уровнях и затруднит чтение всех диаграмм, на которых она присутствует.
Выходом является тоннелирование стрелки на самом нижнем уровне. Такое тоннелирование называется «не-в-родитсльской-диаграмме».
Для чего служит тоннелирование дуг
BPwin и Erwin. CASE-средства для разработки информационных систем
Сергей Владимирович Маклаков
Книга состоит из шести глав и приложения.
Первая глава посвящена изложению основ методологии функционального моделирования и построению моделей IDEFO, IDEF3 и DFD с помощью PLATINUM BPwin.
Во второй главе излагаются принципы построения модели данных и генерации кода серверной и клиентской части приложения с помощью PLATINUM ERwin.
В третьей главе рассматривается интеграция модели данных и функциональной модели с помощью встроенной функциональности BPwin и ERwin.
В четвертой главе описываются методы коллективной работы над большими проектами и специализированный репозиторий PLATINUM ModelMart, предназначенный для хранения, документирования, слияния, интеграции и сравнения моделей, созданных в BPwin и ERwin.
Пятая глава посвящена языку объектного проектирования UML, построению объектной модели с помощью Rational Rose и технологии связывания объектной модели с моделью данных ERwin.
В шестой главе рассматривается техника создания качественных отчетов по моделям процессов и данных с помощью специализированного генератора отчетов PLATINUM RPTwin.
Приложение содержит список макросов ERwin.
Автор приносит благодарность фирме «Интерфейс Ltd.» и лично Б.Н.Гайфуллину за постоянную поддержку и возможность использования лицензионных программных средств.
Особую признательность автор выражает своей жене Елене за помощь в оформлении рукописи.
А. Реализацию проектов по созданию ИС принято разбивать на стадии анализа (прежде чем создавать ИС, необходимо понять и описать бизнес-логику предметной области), проектирования (необходимо определить модули и архитектуру будущей системы), непосредственного кодирования, тестирования и сопровождения. Известно, что исправление ошибок, допущенных на предыдущей стадии, обходится примерно в 10 раз дороже, чем на текущей, откуда следует, что наиболее критическими являются первые стадии проекта. Поэтому крайне важно иметь эффективные средства автоматизации ранних этапов реализации проекта.
В. Проект по созданию сложной ИС невозможно реализовать в одиночку. Коллективная работа существенно отличается от индивидуальной, поэтому при реализации крупных проектов необходимо иметь средства координации и управления коллективом разработчиков.
С. Жизненный цикл создания сложной ИС сопоставим с ожидаемым временем ее эксплуатации. Другими словами, в современных условиях компании перестраивают свои бизнес-процессы примерно раз в два года, столько же требуется (если работать в традиционной технологии) для создания ИС. Может оказаться, что к моменту сдачи ИС она уже никому не нужна, поскольку компания, ее заказавшая, вынуждена перейти на новую технологию работы. Следовательно, для создания ИС жизненно необходим инструмент, значительно (в несколько раз) уменьшающий время разработки ИС.
На современном рынке средств разработки ИС достаточно много систем, в той или иной степени удовлетворяющих перечисленным требованиям. В настоящей книге рассматривается вполне конкретная технология разработки, основывающаяся на решениях фирмы PLATINUM technology (http://www.platinum.com), которая является, по мнению автора, одной из лучших на сегодняшний день по критерию стоимость/эффективность.
Рассматриваемые в книге CASE-средства ERwin и BPwin были разработаны фирмой Logic Works. После слияния в 1998 году Logic Works с PLATINUM technology они выпускаются под логотипом PLATINUM technology.
Рис. 1. Общая схема взаимодействия инструментальных средств PLATINUM technology и Rational Software
Для чего служит тоннелирование дуг
Существуют следующие типы тоннелирования:
(1) Стрелка, помещенная в тоннель там, где она присоединяется к блоку, означает, что данные, выраженные этой стрелкой, не обязательны на следующем уровне декомпозиции.
(2) Стрелка, помещаемая в тоннель на свободном конце означает, что выраженные ею данные отсутствуют на родительской диаграмме.
Вновь внесенная граничная стрелка на диаграмме декомпозиции нижнего уровня изображается в квадратных скобках [ ] и автоматически не появляется на диаграмме верхнего уровня. Такая стрелка называется неразрешенной (unresolved).
Для миграции такой стрелки на диаграмму верхнего уровня необходимо в окне Border Arrow Editor выбрать опцию Resolve it border arrow. Для тоннелирования необходимо выбрать опцию Change it to resolved rounded tunnel. В этом случае стрелка не попадет на другую диаграмму.
Если на диаграмме нижнего уровня необходимо изобразить малозначимые объекты, то изображающие их стрелки можно поместить в тоннель на самом нижнем уровне.
49. Создайте граничную стрелку выхода Маркетинговые материалы, блока Продажи и маркетинг (см. 18-22).
50. Созданная граничная стрелка автоматически не попадает на диаграмму верхнего уровня и имеет квадратные скобки [ ].
51. Выполните мигрирование стрелки на верхний уровень: выберите квадратные скобки [ ] на неразрешенной стрелке, МП, выберите Arrow Tunnel, выберите Resolve it to Border Arrow, нажмите ОК.
52. Результат должен быть, как на рисунке Б (приложение 2).
Какой инструмент необходимо выбрать, чтобы с его помощью произвести декомпозицию блока?
ЛАБОРАТОРНАЯ РАБОТА № 2
Декомпозиция контекстной диаграммы
С помощью этой лабораторной работы Вы сможете:
· освоить правила построения дуг и тоннелирования стрелок.
Теоретические сведения
Декомпозиция
& После создания контекстной диаграммы, которая представляет собой описание контекста моделируемой системы, проводится функциональная декомпозиция – система разбивается на подсистемы и каждая подсистема описывается в том же синтаксисе, что и система в целом. Затем каждая подсистема разбивается на более мелкие и так до достижения нужного уровня подробности. В результате такого разбиения, каждый фрагмент системы изображается на отдельной диаграмме декомпозиции. Диаграмма декомпозиции предназначена для детализации работы.
При декомпозиции процесса все стрелки, входящие или исходящие из него, должны быть перенесены на диаграмму нижнего уровня и использованы при ее построении. При этом запрещены всякие новые стрелки, выходящие за пределы новой диаграммы, кроме специальных, так называемых «тоннелированных» стрелок.
Создание диаграммы А0
Диаграмма верхнего уровня создается путем декомпозиции основной функции контекстной диаграммы. На диаграмме декомпозиции функции нумеруются автоматически слева направо. Номер функции показывается в правом нижнем углу. В левом верхнем исчезает небольшая диагональная черта, которая показывает, что данная функция была декомпозирована.
Практическое задание
Задание 10. Детализация процесса «Изготовление мебели».
Откройте файл Lab1.bp1, сохраненный на предыдущем уроке.
Следующим шагом является детализация контекстного процесса с помощью диаграммы верхнего уровня. Эта диаграмма содержит в себе четыре процесса:
1) Процесс 1.1 – ПЕРЕРАБОТКА СЫРЬЯ.
2) Процесс 1.2 – ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ.
3) Процесс 1.3 – СБОРКА ИЗДЕЛИЯ.
4) Процесс 1.4 – КОНТРОЛЬ КАЧЕСТВА.
Произведите детализацию процесса «Изготовление мебели», задав нужное количество новых блоков. Для этого:
1. Щелкните по блоку «Изготовление мебели» и выберите инструмент 
.
2. В диалоговом окне введите число, на которое будет произведена декомпозиция – 4.
3. Укажите тип диаграммы IDEF0 (рис. 2.1.) и нажмите OK.
Рис. 2.1. Диалоговое окно декомпозиции блока
4. Укажите названия новых блоков («Переработка сырья», «Изготовление деталей», «Сборка изделия», «Контроль качества»).
При декомпозиции функции входящие в нее и исходящие из нее дуги автоматически появляются на диаграмме декомпозиции (миграция дуг), но при этом не касаются блоков. Такие стрелки называются несвязанными и воспринимаются в BPwin как синтаксическая ошибка (см. рис.2.2.).
Рис. 2.2. Декомпозиция верхнего уровня
Определим входные и выходные потоки для новых процессов.
Процесс 1.1. ПЕРЕРАБОТКА СЫРЬЯ:
2) Вход – ОТБРАКОВАННЫЕ ИЗДЕЛИЯ.
3) Выход – ЗАГОТОВКИ.
Произведем процесс связывания мигрирующих дуг:
5. Выберите инструмент 
рисования дуг.
6. Щелкните мышью по наконечнику входного потока СЫРЬЁ.
7. Щелкните по входной стороне блока ПЕРЕРАБОТКА СЫРЬЯ.
Вход – ОТБРАКОВАННЫЕ ИЗДЕЛИЯ построим немного позже.
Для построения выходного потока ЗАГОТОВКИ выполните действия:
8. Выберите инструмент рисования дуг.
9. Щелкните левой кнопкой мышки по выходной стороне блока ПЕРЕРАБОТКА СЫРЬЯ.
10. Затем щелкните по входной стороне блока ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ.
11. Выберите инструмент 
текст, в контекстном меню – команду Name,укажите название дугиЗАГОТОВКИ.
12. Проверьте себя (рис. 2.3.).
Рис. 2.3. Фрагмент диаграммы
Задание 11. Детализация процесса «Изготовление мебели».
1. Самостоятельно выполните детализацию процессов:
Процесс 1.2. ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ:
2) Выход – ГОТОВЫЕ ДЕТАЛИ.
Процесс 1.3. СБОРКА ИЗДЕЛИЯ:
1) Вход – ГОТОВЫЕ ДЕТАЛИ.
2) Выход – СОБРАННОЕ ИЗДЕЛИЕ.
Процесс 1.4. КОНТРОЛЬ КАЧЕСТВА:
1) Вход – СОБРАННОЕ ИЗДЕЛИЕ.
2) Выход – ГОТОВОЕ ИЗДЕЛИЕ.
4) Выход – ПРОИЗВОДСТВЕННЫЕ ОТХОДЫ
После того, как эта работа будет проделана, пригласите преподавателя и продемонстрируйте ему результат.
Задание 12. Смена направления дуги.
На Выходе БРАК не выходит за границу модели, а возвращается в процесс ПЕРЕРАБОТКА СЫРЬЯ:
1. Удалите дуги ОТБРАКОВАННЫЕ ИЗДЕЛИЯ и БРАК.
2. Выберите инструмент рисование дуг.
3. Щелкните левой кнопкой мыши на Выходе блока КОНТРОЛЬ КАЧЕСТВА.
4. Щелкните левой кнопкой на Входе блока ПЕРЕРАБОТКА СЫРЬЯ.
5. Назовите новую дугу – БРАК (рис. 2.4.).
Рис. 2.4. Процесс декомпозиции
Задание 13. Построение ответвлений дуг.
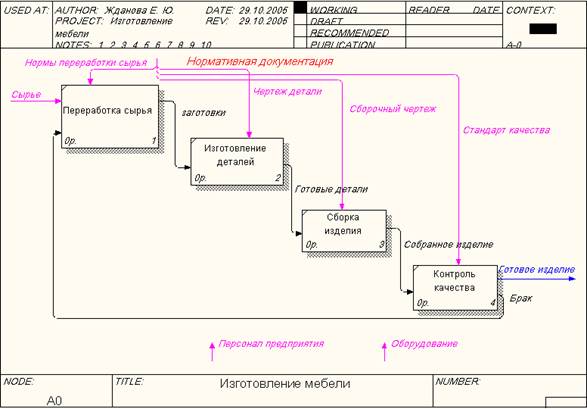
Переработка сырья, изготовление деталей, сборка изделия, контроль качества осуществляются согласно Нормативным документам, поэтому у управляющей стрелки НОРМАТИВНАЯ ДОКУМЕНТАЦИЯ появятся ответвления: НОРМЫ ПЕРЕРАБОТКИ СЫРЬЯ, ЧЕРТЕЖ ДЕТАЛИ, СБОРОЧНЫЙ ЧЕРТЕЖ, СТАНДАРТ КАЧЕСТВА.
1. Выберите инструмент рисование дуг.
2. Щелкните мышью по наконечнику входного потока НОРМАТИВНАЯ ДОКУМЕНТАЦИЯ.
3. Щелкните по входной стороне блока ПЕРЕРАБОТКА СЫРЬЯ.
4. Самостоятельно выполните ответвления дуги НОРМАТИВНАЯ ДОКУМЕНТАЦИЯ на блоки ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ, СБОРКА ИЗДЕЛИЯ, КОНТРОЛЬ КАЧЕСТВА.
5. Проверьте себя(рис. 2.5.).
Рис. 2.5. Ответвления дуги НОРМАТИВНАЯ ДОКУМЕНТАЦИЯ
Задание 14. Построение дуг Персонал предприятия, Оборудование.
Дуги ПЕРСОНАЛ ПРЕДПРИЯТИЯ и ОБОРУДОВАНИЕ для всех процессов будут одинаковые.
1. Самостоятельно соедините каждую дугу с каждым блоком, укажите ее имя.
2. Проверьте себя (рис. 2.6.).
Рис. 2.6. Построение дуг ПЕРСОНАЛ ПРЕДПРИЯТИЯ и ОБОРУДОВАНИЕ
После того, как эта работа будет проделана, пригласите преподавателя и продемонстрируйте ему результат.
Задание 15. «Тоннелирование» стрелок.
1. В Процессе 1.2. ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ постройте новую граничную дугу, которой обозначьте Выход – ПРОИЗВОДСТВЕННЫЕ ОТХОДЫ.
Вновь внесенные граничные дуги на диаграмме декомпозиции нижнего уровня изображаются в квадратных скобках и автоматически не появляются на диаграмме верхнего уровня.
Для их «перетаскивания» наверх нужно:
2. Выбрать инструмент 
редактирования.
3. Кликнуть правой кнопкой мыши по квадратным скобкам.
4. Выбрать в контекстном меню пункт Arrow Tunnel.
5. В появившемся диалоге Border Arrow Editor (рис. 2.7.) щелкнуть по кнопке Resolve it to border arrow для миграции стрелки на диаграмму верхнего уровня или по кнопке Change it to resovled rounded tunnel для «тоннелирования» дуги.
Рис. 2.7. Диалог Border Arrow Editor
Тоннельная дуга изображается с круглыми скобками на конце и не попадет на другую диаграмму (рис. 2.8.). Такое тоннелирование может быть применено для изображения малозначимых стрелок.
Рис. 2.8. Граничная дуга
6. Отправьте созданную дугу «Производственные отходы» в тоннель.
Задание 16. Создание обратной связи по управлению.
Качество изделия может быть повышено путем непосредственного регулирования процессами изготовления деталей и сборки мебели в зависимости от результата (выхода) работы КОНТРОЛЬ КАЧЕСТВА.
Обратная связь по управлению свидетельствует об эффективности бизнес-процесса и создается следующим образом:
1. Выберите инструмент рисование дуг.
2. Щелкните мышью по выходу КОНТРОЛЬ КАЧЕСТВА.
3. Щелкните по управлению блоков ИЗГОТОВЛЕНИЕ ДЕТАЛЕЙ, СБОРКА ИЗДЕЛИЯ.
4. Выберите инструмент 
текст.
5. Назовите обратную связь РЕКОМЕНДАЦИИ.
После выполнения работы у вас должна получиться следующая диаграмма (рис. 2.9.):
Рис. 2.9. Диаграмма декомпозиции блока ИЗГОТОВЛЕНИЕ МЕБЕЛИ
Задание 17. Сохранение полученной диаграммы.
1. В меню Fileвыберите Save as.
2. Укажите путь к своей папке и имя файла Lab2.bp1.
После того, как эта работа будет проделана, пригласите преподавателя и продемонстрируйте ему результат.
Контрольные вопросы
Тестовое задание
1. В каком порядке надо располагать блоки на диаграмме детализации:
b) обязательно справа налево;
c) в соответствии с уровнем сложности последующей детализации;
d) в соответствии с их доминированием;
e) все ответы правильные.
2. Для чего предназначена диаграмма детализации процесса:
a) для обозначения тоннелированных дуг;
b) для описания контекста моделируемой системы;
c) для детализации работы;
d) все ответы правильные.
3. Как создается диаграмма верхнего уровня:
a) путем декомпозиции одной из функций контекстной диаграммы;
b) путем декомпозиции основной функции контекстной диаграммы;
c) путем декомпозиции диаграмм нижнего уровня;
d) путем декомпозиции одной из функций на диаграмме верхнего уровня;
e) правильного ответа нет.
Какой инструмент необходимо выбрать, чтобы с его помощью произвести декомпозицию блока?
a) 
;
b) 
;
c) 
;
d) 
;
e) 
.