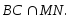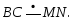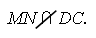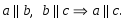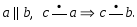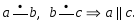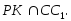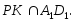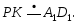Для доказательства параллельности двух прямых достаточно утверждать что они
Пожалуйста, решите как можно быстрее! СРОЧНО! Заранее спасибо!
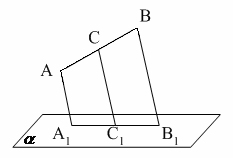
1.Точки А, В, С и D не лежат в одной плоскости. Тогда прямые АВ и СD…
1)пересекающиеся; 2)параллельные; 3)скрещивающиеся.
2.Какое утверждение о прямых верное?
3.Для доказательства параллельности двух прямых достаточно утверждать, что они…
1)не пересекаются; 2)перпендикулярны некоторой прямой; 3)не пересекаются и лежат в одной плоскости.
4.Какое утверждение верное?
1)a∥b, b∥c⇒a∥c.2)a∥b, c∸a ⇒ c∸b.3)a∸b, b∸c ⇒ a∥c.
5.Точка F ∉ в плоскости параллелограмма АВСD, М – середина DF, N – середина BF. Тогда прямые АМ и СN…
1)скрещиваются; 2)пересекаются; 3)параллельны.
6.Прямая а∥α. Тогда неверно, что…
1)прямая а ∥ любой прямой, в плоскости α;
2)прямая а не ∩ ни одну прямую, в плоскости α;
3)существует прямая, в плоскости α, ∥ прямой а.
7.Какое утверждение неверное?
1)если плоскость проходит через данную прямую, ∥ другой плоскости, и ∩ эту плоскость, то линия ∩плоскостей ∥данной прямой.
2)если прямая ∥ двум ∩ плоскостям, то она ∥ их линии пересечения.
3)прямые, ∥одной плоскости, ∥.
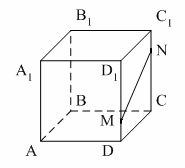
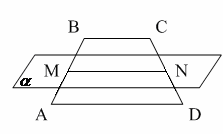
8.Средняя линия MN трапеции АВСD с основаниями ВС и AD лежит в плоскости α. Вершина А ∉ данной плоскости. Тогда прямая ВС…
1) плоскости α;2) ∩ плоскость α;3) ∥ плоскости α.
9.Точка М ∉а. Тогда неверно, что через точку М можно провести…
1)только одну прямую, не ∩ прямую а;
2)только одну прямую, ∥ прямой а;
3)бесконечно много прямых, не ∩ прямую а.
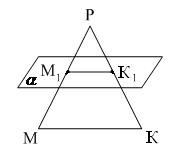
10.Дан Δ МКР. Плоскость, ∥ прямой МК, ∩ МР в точке М1, РК – в точке К1. МК = 18 см, МР: М1Р = 12:5. Тогда длина отрезка М1К1 равна…
Тест по геометрии
тест по теме: «Взаимное расположение прямых в пространстве. Параллельность прямых, прямой и плоскости»
Сегодня в математике при оценивании результатов по геометрии в школе часто применяют тестирование. Применяя тестирование в преподавании, предоставляется возможность глубоко оценить уровень усвоения материала по данной теме. Тест состоит из 2 уровней: с выбором ответа и решение задач.
Содержимое разработки
тест по теме: «Взаимное расположение прямых
в пространстве. Параллельность прямых,
прямой и плоскости»
1. Точки A, B, С и D не лежат в одной плоскости. Тогда прямые AB и CD…
2. Какое утверждение о прямых верное?
1) 
2) 
3) 
3. Для доказательства параллельности двух прямых достаточно утверждать, что они…
2) перпендикулярны некоторой прямой;
3) не пересекаются и лежат в одной плоскости.
4. Какое утверждение неверное?
1) 
2) 
3) 
5. Точка F не лежит в плоскости параллелограмма ABCD, M – середина DF, N – середина BF. Тогда прямые AM и CN…
6. Прямая а параллельна плоскости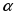 
. Тогда неверно, что…
1) прямая а параллельна любой прямой, лежащей в плоскости ;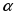
2) прямая а не пересекает ни одну прямую, лежащую в плоскости ;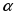
3) существует прямая, лежащая в плоскости 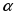, параллельная прямой а.
7. Какое утверждение неверное?
1) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2) Если прямая параллельна двум пересекающимся плоскостям, то она параллельна их линии пересечения.
3) Прямые параллельные одной плоскости параллельны
8. Средняя линия MN трапеции ABCD лежит в плоскости 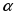. Вершина А не принадлежит данной плоскости. Тогда прямая BC…
1) лежит в плоскости ;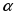
2) пересекает плоскость ;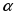
3) параллельна плоскости .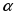
9. Точка M не лежит на прямой а. Тогда неверно, что через точку M можно провести…
1) только одну прямую, не пересекающую прямую а;
2) только одну прямую, параллельную прямой а;
3) бесконечно много прямых, не пересекающих прямую а.
1. Дан треугольник MKP. Плоскость, параллельная прямой MK пересекает MP в точке M1, PK – в точке K1. MK = 18 см, MP : M1P = 12 : 5. Тогда длина отрезка M1K1 равна…
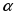
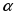
2. Через концы отрезка АВ, не пересекающего плоскость , и точку С – середину этого отрезка, проведены параллельные прямые, пересекающие плоскость в точках А1, В1 и С1 соответственно. АА1 = 6 см, СС1 = 9 см. Тогда длина отрезка ВВ1 равна…
3. Плоскость, параллельная основаниям трапеции ABCD, пересекает стороны AD и CD в точках M и N соответственно. CN = ND. AD = 6 см, ВС = 4 см. Тогда длина отрезка MN равна…
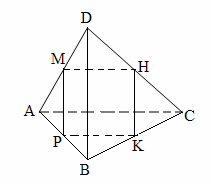
4. M, H, P – середины соответственно сторон AD, DC, AB. KH || (ABD). AC = 8 см, BD = 10 см. Периметр четырёхугольника MHKP равен…
тест по теме: «Взаимное расположение прямых
в пространстве. Параллельность прямых,
прямой и плоскости»
2. Нельзя провести плоскости через две прямые, если они…
3. Какое утверждение о прямых неверное?
1) 
2) 
3) 
4. Точка D не лежит в плоскости треугольника АВС, K – середина DC. Тогда прямые AD и BK…
5. Какое утверждение верное?
1) Две прямые называются параллельными, если они не имеют общих точек.
2) Две прямые, параллельные третье прямой, параллельны.
3) Две прямые, перпендикулярные третьей прямой, параллельные.
Тогда прямые AB и CD…
7. Какое утверждение верное?
1) Если она из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
2) Если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая параллельна данной плоскости.
3) Если две прямые параллельны данной плоскости, то они параллельны.
8. Точки M и N соответственно середины сторон AB и BC треугольника АВС. Прямая MN лежит в плоскости 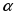. Точка В не принадлежит данной плоскости. Тогда прямая АС…
1) лежит в плоскости ;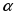
2) пересекает плоскость ;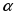
3) параллельна плоскости .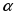
9. Какое утверждение неверное?
1) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
2) Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в этой плоскости.
3) Если прямая параллельна плоскости, то она не пересекает ни одну прямую, лежащую в этой плоскости.
1. Дан треугольник ВСЕ. Плоскость, параллельная СЕ, пересекает ВЕ в точке Е1, ВС – в точке С1. ВС = 28 см, С1Е1 : СЕ = 3 : 8. Тогда длина отрезка ВС1 равна…
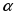
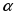
2. Через концы отрезка АВ, не пересекающего плоскость , и точку С – середину этого отрезка, проведены параллельные прямые, пересекающие плоскость в точках А1, В1 и С1 соответственно.
Тогда длина отрезка ВВ1 равна…
3. Плоскость, параллельная основаниям AD и ВС трапеции ABCD, пересекает стороны АВ и CD в точках M и N соответственно. AM = MB. AD = 10 см, ВС = 6 см. Тогда длина отрезка MN равна…
4. M, H, K – середины соответственно сторон AD, DC, CB.
AC = 10 см, BD = 8 см. Периметр четырёхугольника MHKP равен…
тест по стереометрии
тест
1) Через любые три точки проходит плоскость, и притом только одна.
2) Через две пересекающиеся прямые проходит плоскость, и притом только одна.
3) Через две параллельные прямые проходит плоскость, и притом только одна.
2. Две различные плоскости не могут иметь…
3) три общих точки, не лежащие на одной прямой.
1) 
2) 
3) 
4. Через прямые m и k можно провести более одной плоскости. Тогда прямые m и k …
1) хотя бы одну плоскость;
2) только одну плоскость;
3) не более одной плоскости.
6. Точки A, B, С и D не лежат в одной плоскости. Тогда прямые AB и CD…
7. Для доказательства параллельности двух прямых достаточно утверждать, что они…
2) перпендикулярны некоторой прямой;
3) не пересекаются и лежат в одной плоскости.
1) 
2) 
3) 
9. Точка F не лежит в плоскости параллелограмма ABCD, M – середина DF, N – середина BF. Тогда прямые AM и CN…
1) прямая а параллельна любой прямой, лежащей в плоскости 
;
2) прямая а не пересекает ни одну прямую, лежащую в плоскости 
;
3) существует прямая, лежащая в плоскости , параллельная прямой а.
1) Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2) Если прямая параллельна двум пересекающимся плоскостям, то она параллельна их линии пересечения.
3) Прямые параллельные одной плоскости параллельны.
12. Средняя линия MN трапеции ABCD лежит в плоскости 
. Вершина А не принадлежит данной плоскости. Тогда прямая BC…
1) лежит в плоскости 
;
2) пересекает плоскость 
;
3) параллельна плоскости 
.
13. Точка M не лежит на прямой а. Тогда неверно, что через точку M можно провести…
1) только одну прямую, не пересекающую прямую а;
2) только одну прямую, параллельную прямой а;
3) бесконечно много прямых, не пересекающих прямую а.
1) Если одна из двух прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
2) Если две прямые перпендикулярны к третьей прямой, то они параллельны.
3) Если две прямые перпендикулярны к плоскости, то они параллельны.
1) перпендикулярна плоскости 
;
2) параллельна плоскости ;
3) лежит в плоскости.
17. 
Тогда прямые a и b не могут быть…
18. Прямая перпендикулярна плоскости круга, если она перпендикулярна двум…
19. Линейным углом двугранного угла нельзя назвать угол, возникающий при пересечении двугранного угла плоскостью, перпендикулярной…
1) ребру двугранного угла;
2) одной из граней двугранного угла;
3) граням двугранного угла.
1) Не может ребро двугранного угла быть не перпендикулярным плоскости его линейного угла.
2) Не могут две плоскости, перпендикулярные к одной плоскости, быть непараллельными.
3) Не могут две плоскости, перпендикулярные к одной прямой, быть непараллельными.
1) 
2) 
3) 
22. Какое утверждение неверное?
1) Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
2) Если плоскости перпендикулярны, то линия их пересечения перпендикулярна любой прямой, лежащей в одной из данных плоскостей.
3) Плоскость, перпендикулярная линии пересечения двух данных плоскостей, перпендикулярна к каждой из этих плоскостей.
23. Не может плоскость быть не перпендикулярной данной плоскости, если она проходит через прямую…
1) параллельную данной плоскости;
2) перпендикулярную данной плоскости;
3) не перпендикулярную данной плоскости.
24. Количество двугранных углов параллелепипеда равно …
25. 
26. 
Прямые CD и CF не будут перпендикулярными, если ABCD будет…
27. 
Прямые DM и ВС будут перпендикулярными, если АM будет…
тест
1) любые три точки лежат в одной плоскости;
2) любые четыре точки не лежат в одной плоскости;
3) через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна.
1) 
2) 
3) 
1) пересекает две стороны треугольника;
2) проходит через одну из вершин треугольника;
3) содержит одну из сторон треугольника.
7. Сколько общих точек, не лежащих на одной прямой, не могут иметь две различные плоскости?
1) хотя бы одну из данных прямых;
2) только одну из данных прямых;
3) две данные прямые.
1) не лежат на одной прямой;
2) лежат на одной прямой;
7. Нельзя провести плоскости через две прямые, если они…
8. Точка D не лежит в плоскости треугольника АВС, K – середина DC. Тогда прямые AD и BK…
1) Две прямые называются параллельными, если они не имеют общих точек.
2) Две прямые, параллельные третье прямой, параллельны.
3) Две прямые, перпендикулярные третьей прямой, параллельные.
10. Какое утверждение верно е?
1) Если она из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
2) Если одна из двух параллельных прямых параллельна данной плоскости, то и другая прямая параллельна данной плоскости.
3) Если две прямые параллельны данной плоскости, то они параллельны.
11. Точки M и N соответственно середины сторон AB и BC треугольника АВС. Прямая MN лежит в плоскости 
. Точка В не принадлежит данной плоскости. Тогда прямая АС…
1) лежит в плоскости 
;
2) пересекает плоскость 
;
3) параллельна плоскости .
12. Какое утверждение неверное?
1) Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
2) Если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в этой плоскости.
3) Если прямая параллельна плоскости, то она не пересекает ни одну прямую, лежащую в этой плоскости.
13. Прямая называется перпендикулярной к плоскости, если она перпендикулярна…
1) к одной прямой, лежащей в плоскости;
2) к двум прямым, лежащим в плоскости;
3) к любой прямой, лежащей в плоскости.
14. 
Тогда прямые a и b не могут быть…
15. Диагональ АС квадрата ABCD перпендикулярна некоторой плоскости 
1) перпендикулярна плоскости ;
2) параллельна плоскости ;
3) лежит в плоскости .
16. 
Прямые b и с не могут быть…
1) Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
2) Через точку, не лежащую на данной прямой, можно построить только одну плоскость, перпендикулярную данной прямой.
3) Через точку, не лежащую на данной прямой, можно построить только одну прямую, перпендикулярную данной прямой.
18. 
Тогда 
– это линейный угол двугранного угла между плоскостями 
и 
, если…
1) 
2) 
3) 
19. Какое утверждение верное?
1) Не может ребро двугранного угла быть не перпендикулярным любой прямой, лежащей в плоскости его линейного угла.
2) Не могут быть две плоскости, перпендикулярные третьей, непараллельными.
3) Не могут быть две плоскости, перпендикулярные одной плоскости, непараллельными.
20. Какое утверждение верное?
1) 
2) 
3) 
21. Какое утверждение верное?
1) 
2) 
3) 
22. Какое утверждение верное?
1) Нельзя через точку пространства провести три плоскости, каждые две из которых взаимно перпендикулярны.
2) Не существует прямой, пересекающей две данные скрещивающиеся прямые и перпендикулярной каждой из них.
3) Не может плоскость быть не перпендикулярной данной плоскости, если она проходит через прямую, перпендикулярную данной плоскости.
23. Количество двугранных углов тетраэдра равно…
24. 
Прямые АС и FO не будут перпендикулярными, если ABCD будет…
1) точка пересечения высот;
2) центр описанной около 
окружности;
3) центр вписанной в 
окружности.
27. АМ=АК