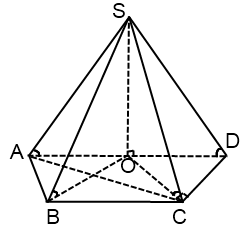
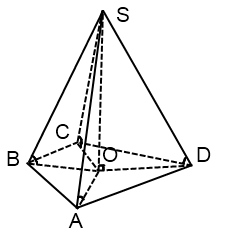
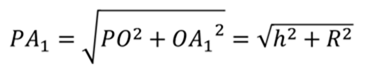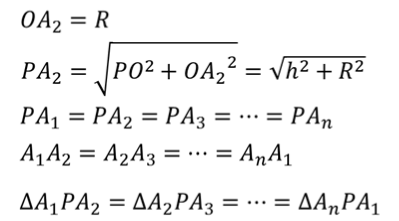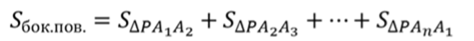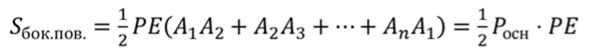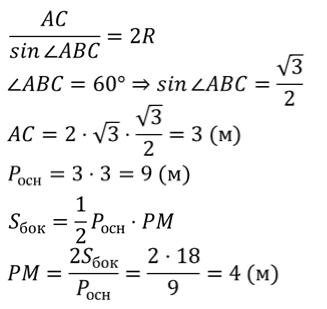Доказать что боковые ребра правильной пирамиды равны

Пирамида. Правильная пирамида

Урок 27. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Пирамида. Правильная пирамида»

С пирамидой мы с вами знакомились в курсе геометрии базовой школы. Давайте вспомним, какой многогранник мы назвали пирамидой и основные элементы пирамиды.

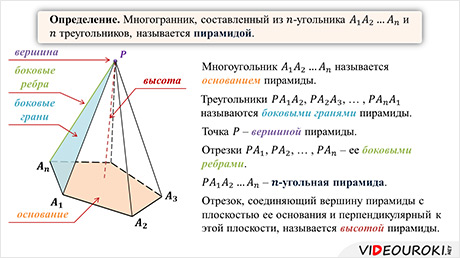
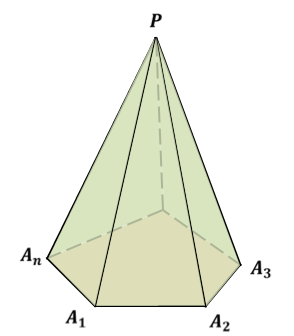
Итак, рассмотрим многоугольник A₁A₂…A_n и точку P, не лежащую в плоскости этого многоугольника. Соединим точку ПЭ отрезками с вершинами многоугольника. В итоге получим n треугольников: PA₁A₂, PA₂A₃, …, PA_nA₁. Многогранник, составленный из n-угольника A₁A₂…A_n и этих n треугольников, называется пирамидой.

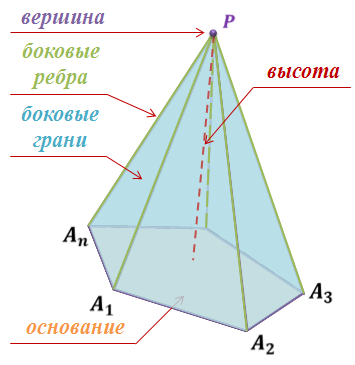
Многоугольник A₁A₂…A_n называется основанием пирамиды. Треугольники PA₁A₂, PA₂A₃, …, PA_nA₁ называются боковыми гранями пирамиды. Точка P – вершиной пирамиды, а отрезки PA₁, PA₂,…, PA_n – ее боковыми ребрами.

Пирамиду с вершиной P и основанием A₁A₂…A_n называют n-угольной пирамидой и обозначают так: PA₁A₂…A_n.

Отрезок, соединяющий вершину пирамиды с плоскостью ее основания и перпендикулярный к этой плоскости, называется высотой пирамиды.

Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней. А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.

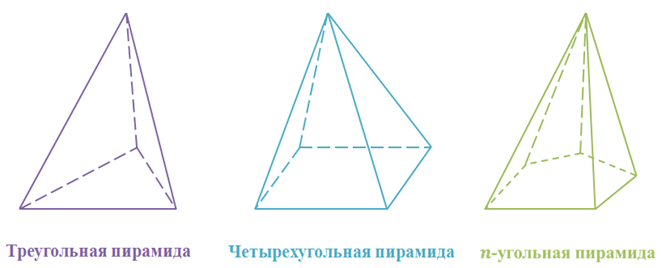
Пирамида в зависимости от того какой многоугольник лежит в основании имеет свое название. Если в основании лежит треугольник, то пирамида называется треугольной. Если четырехугольник – то четырехугольной пирамидой. А если n-угольник, то n-угольной пирамидой.

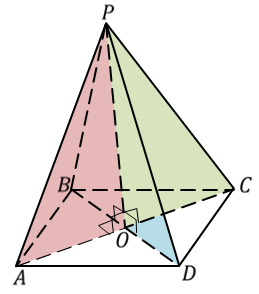
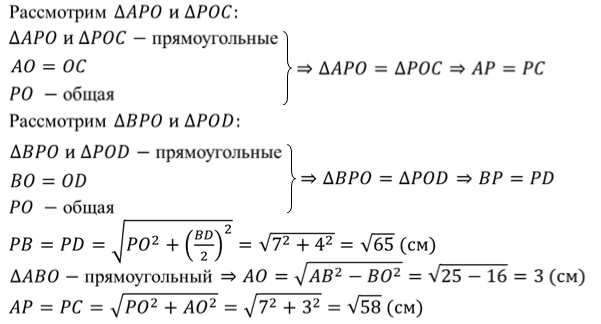
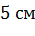
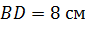
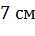
Задача. Основанием пирамиды является ромб, сторона которого равна , а одна из диагоналей равна . Найти длину боковых ребер пирамиды, если высота пирамиды проходит через точку пересечения диагоналей основания и равна .

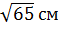
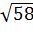
Ответ. , см.

Давайте дадим определение правильной пирамиды.

Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.

На сегодняшнем уроке мы подробно рассмотрим правильные пирамиды.

Сейчас давайте попробуем доказать одно из свойств правильной пирамиды. А именно докажем, что все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

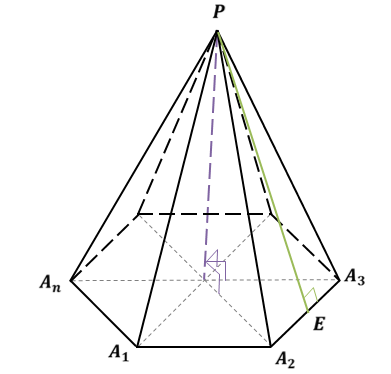
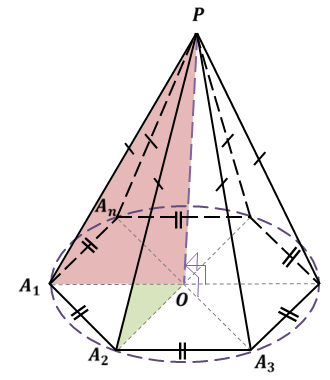
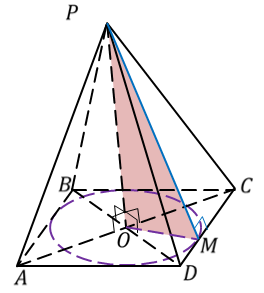
Рассмотрим правильную пирамиду PA₁A₂…A_n. Сначала докажем, что все боковые ребра этой пирамиды равны. Проведем высоту пирамиды.

Поскольку основанием правильной пирамиды является правильный многоугольник, значит, вокруг основания правильной пирамиды можно описать окружность. Тогда каждое боковое ребро пирамиды есть ничто иное, как гипотенуза прямоугольного треугольника, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности. Например, если рассмотреть треугольник OPA₁, то OP равно h, OA₁ равно R.

Таким образом, мы доказали, что боковые ребра правильной пирамиды равны. А значит, боковые грани правильной пирамиды – это равнобедренные треугольники. Поскольку в основании лежит правильный многоугольник, значит, основания боковых граней равны между собой. То есть боковые грани равны между собой по трем сторонам.

Что и требовалось доказать.

Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной пирамиды.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Запишем формулу для вычисления площади боковой поверхности правильной пирамиды.

Мы уже доказали, что боковые грани правильной пирамиды – равные равнобедренные треугольники. Высоты этих треугольников равны апофеме пирамиды. Тогда площадь боковой грани находится по формуле .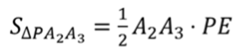

Подставим эти площади в формулу площади боковой поверхности. Вынесем половину апофемы за скобки, тогда в скобках получим периметр основания.

Что и требовалось доказать.

Решим несколько задач.

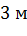
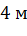
Задача. Радиус окружности, вписанной в основание правильной четырехугольной пирамиды, равен , высота пирамиды равна . Найти площадь боковой поверхности пирамиды.

Решим еще одну задачу.

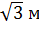
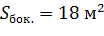
Задача. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен . . Найти длину апофемы.

Подведем итоги урока.

Сегодня на уроке мы вспомнили, какая фигура называется пирамидой. Какие пирамиды называются правильными. Познакомились со свойствами правильных пирамид. Решили несколько задач.

Источник

Узнать ещё

Знание — сила. Познавательная информация

Пирамиды, в которых все боковые ребра равны

Рассмотрим свойства пирамид, в которых все боковые ребра равны, с соответствующими чертежами.

Если все боковые ребра пирамиды равны между собой, то вершина пирамиды проецируется в центр описанной около основания окружности.

Прямоугольные треугольники, образованные высотой пирамиды, боковыми ребрами и их проекциями (равными радиусу описанной окружности), равны. Поэтому также

— все боковые ребра пирамиды образуют с плоскостью основания равные углы;

— все углы, которые боковые ребра образуют с высотой пирамиды, равны.

Решение задач на пирамиду, в которой все боковые ребра равны (либо все боковые ребра образуют равные углы с основанием пирамиды или с высотой пирамиды) начинается с чертежа.

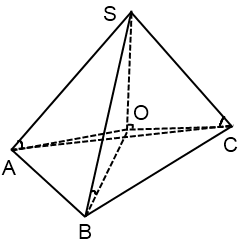
Если основание пирамиды — треугольник.

Центр окружности, описанной около остроугольного треугольника, лежит внутри треугольника.

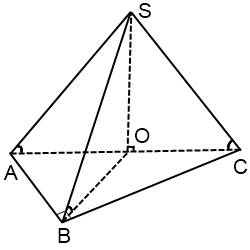
Центр окружности, описанной около тупоугольного треугольника, лежит вне треугольника.

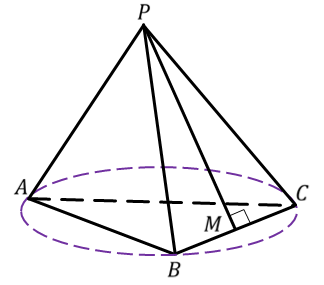
На рисунке тупой угол — это угол B.

Радиус окружности, описанной около произвольного остроугольного либо тупоугольного треугольника ABC, можно найти по следствию из теоремы синусов:

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Радиус описанной около основания окружности в этом случае равен

Отсюда для данного треугольника ABC с прямым углом B

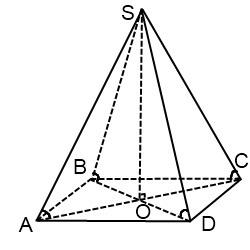
Если основание пирамиды — параллелограмм

Из всех параллелограммов описать окружность можем только около прямоугольника (квадрат — его частный случай). Поэтому, если в задаче сказано, что пирамиде все боковые ребра равны, либо все боковые ребра одинаково наклонены к плоскости основания, либо все боковые ребра образуют с высотой пирамиды равные углы, а в основании — параллелограмм, то это может быть только прямоугольник (квадрат).

Центр описанной около прямоугольника окружности — точка пересечения его диагоналей. Соответственно, радиус R равен половине диагонали прямоугольника.

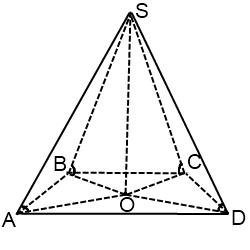
Из всех трапеций описать окружность можно только около равнобочной трапеции.

Радиус описанной окружности ищем как радиус окружности, описанной около одного из треугольников ABC или ACD по одной из формул, приведенных выше.

Если диагональ трапеции перпендикулярна боковой стороне

боковые ребра пирамиды равны

В этом случае центр описанной около трапеции окружности лежит на середине большего основания, а высота пирамиды лежит в боковой грани, содержащей это большее основание.

Радиус R в этом случае — половина гипотенузы прямоугольного треугольника ACD.

Если основание пирамиды — произвольный четырехугольник

Радиус описанной около основания окружности находим как радиус окружности, описанной около одного из треугольников основания: ABC, BCD, ACD или ABD.

Поскольку описать около четырехугольника окружность можно только тогда, когда сумма его противолежащих углов равна 180 градусов, то

Источник

Презентация к уроку

I. Домашнее задание каждый ученик получает на заранее отпечатанных листочках.

Теория: по учебнику п.14.2, стр.110-111,2)и 3 задачи:

II. Устная работа по готовым чертежам. (Каждый ребёнок получает лист А-4 с чертежами треугольной пирамиды).

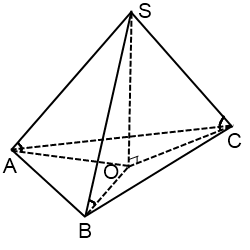
2.1. Докажем 3 (прямые) теоремы. Дано: МАВС треугольная пирамида, МО – высота пирамиды.

1. Ученики доказывают “ простую” теорему из одного условия и одного заключения

2. Используют признак равенства прямоугольных треугольников по катету и гипотенузе

3. Делают вывод: из того что АО = ВО =СО, следует О – центр окружности, описанной около основания.

4.Учитель уточняет формулировки данного обстоятельства “основание пирамиды совпадает с центром окружности, описанной около основания” или “ вершина пирамиды проектируется в центр окружности, описанной около основания.

(к рис.2,3). Заменить условие теоремы, сохранить её заключение. Опираясь на признаки равенства прямоугольных треугольников, ученики приходят к выводу о том, что можно потребовать равенство углов между боковыми рёбрами и плоскостью основания или равенство углов между боковыми рёбрами и высотой пирамиды.

Рисунок 1

Рисунок 2

Рисунок 31)Боковые рёбра равны

Доказать: АО = ВО = СО2)…(углы между боковыми рёбрами и плоскостью основания равны)

Доказать: АО = ВО = СО3) …(углы между боковыми ребрами и высотой пирамиды равны)

2.2. Сформулируем обратные утверждения. Верны ли эти утверждения?

Ученики, используя признаки равенства прямоугольных треугольников, доказывают обратные утверждения. Дано: МАВС треугольная пирамида, МО – высота пирамиды, О – центр окружности, описанной около основания, АО=ВО=СО.

Рисунок 4

Рисунок 5

Рисунок 6Доказать: боковые рёбра равны АМ=ВМ =СМДоказать: углы между боковыми рёбрами и плоскостью основания равныДоказать: углы между боковыми ребрами и высотой пирамиды равны

2.3. Формулировка теоремы для n-угольной пирамиды.

Постановка проблемы: справедливо ли данное утверждение для n-угольной пирамиды? Ученикам предлагается доказать три прямых утверждения по аналогии.

Теорема. В n-угольной пирамиде с равными боковыми рёбрами основание высоты совпадает с центром окружности, описанной около основания; высота составляет равные углы с боковыми ребрами; боковые ребра составляют равные углы с плоскостью основания.

2.4. Работа после доказательства теоремы (взгляд назад).

В – Боковые рёбра пирамиды составляют с плоскостью основания равные углы

С – Боковые рёбра пирамиды составляют с высотой пирамиды равные углы

М – Основание пирамиды совпадает с центром окружности, описанной около основанияУчитывая все 6 простых теорем, ученики подводятся к выводу

А, А, А

В, В, В ,

М, М ,М

С, С, С

2. Учитель показывает утверждении А( В, С,М), ученик формулирует 3 простые теоремы.

III. Формулировка темы урока. (Свойства пирамиды с равными боковыми ребрами).

Какая же тема сегодняшнего урока? (Любое из утверждений А, В, С, М может быть принято за тему урока).

IV. Составление алгоритма

Алгоритм решения двух шаговых задач.

1. Наличие в условии задачи одного из условий (А,В,С,). Из этих условий вытекает М.

2. Решить основание (найти радиус окружности, описанной около основания).

3. Решить прямоугольный треугольник, например, МОА.1. Составление алгоритма.

2. Актуализация знаний:

а) центр окружности, описанной около основания – точка пересечения серединных перпендикуляров к сторонам треугольника;

б) расположение центра описанной окружности в остроугольном, тупоугольном, прямоугольном треугольниках;

в) формула S = .

V. Применение свойств пирамиды с равными боковыми ребрами к решению задач.

Найти высоту пирамиды.

Рисунок 81.Каждый ученик получает лист с условиями задач для решения

2. Стереометрический чертёж не делаем.

Решение. Работаем по алгоритму:

Наличие условия “ В”

Рисунок 9Решение. Работаем по алгоритму:

1. Наличие условия “А”.

Рисунок 10Решение. Работаем по алгоритму:

1. Наличие условия “ С”

О – вне треугольника,

АО – серединный перпендикуляр к ВС, треугольник АОС равносторонний, АВ =,

R = .

3.Строим треугольник АМО, МО = = 6 Ответ: 6

VI. Итог урока подвести при решении задач:

1. В основании пирамиды лежит трапеция, боковые рёбра равны. Определить вид трапеции (равнобедренная).

2. В основании пирамиды лежит параллелограмм, углы между боковыми рёбрами и плоскостью основания равны. Определить вид параллелограмма( прямоугольник).

3. В основании пирамиды лежит ромб. Углы между боковыми рёбрами и высотой пирамиды равны. Найти углы ромба. (90 о ).

Источник

Пирамида

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Виды пирамид

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Источник