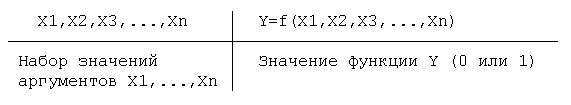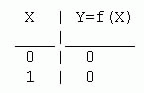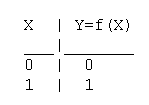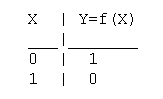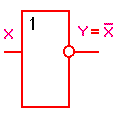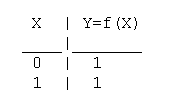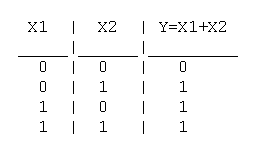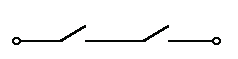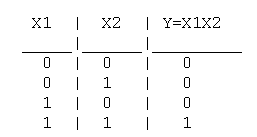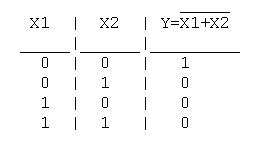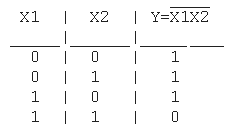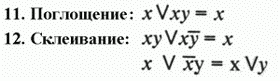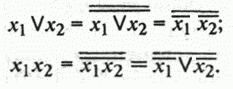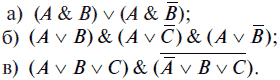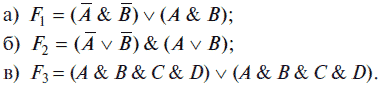Доказать что число логических функций двух логических переменных равно 16
Логические функции от двух переменных



Таблицы истинности
Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.
Истинность или ложность сложных высказываний, образованных в результате выполнения логических операций над простыми высказываниями, не зависит от смыслового содержания исходных высказываний и определяется только их значениями (истинностью или ложностью).
Определим количество различных логических функций с заданным числом переменных п. Логическая функция на каждом наборе переменных принимает значение 0 или 1.
Следовательно, отличающихся друг от друга функций может быть ровно столько, сколько существует различных комбинаций из m = 2 n нулей и единиц.
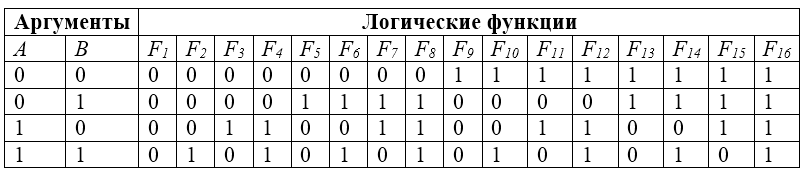
Пусть п = 2. Существует 16 различных логических функций от двух переменных. Рассмотрим их подробно:
| Аргу-менты | Функции | ||||||||||||||||
| X1 | X2 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 |
F3 — отрицательные импликации X1 и X2.
F4 — функция, повторяющая переменная X1.
F7 — строгая дизъюнкция или отрицание эквивалентности
(неравнозначность) переменных X1 и X2. Значение этой функции получается поразрядным сложением двоичных переменных X1 и X2 по модулю 2, то есть без учета переноса в старший разряд.
F9 — отрицание дизъюнкции (функция ИЛИ-НЕ); эта функция называется также функцией Пирса («стрелка» Пирс).
F11 — отрицание переменной X2.
F15 — отрицание конъюнкции (функция И-НЕ); эта функция называется также функцией Шеффера («штрих» Шеффера).
С увеличением числа аргументов количество логических функций резко возрастает. Так, при п = 3 их будет уже 256. Но изучать их все нет никакой необходимости. Дело в том, что функция любого количества переменных может быть выражена через функции только двух переменных. Делается это с помощью приема суперпозиции, состоящего в том, что, во-первых, на место переменных подставляются функции, во-вторых, переменные меняются местами.
Минимальное количество функций двух переменных, через которое можно выразить все другие логические функции, называетсяфункционально полным набором логических функций.
Вот несколько примеров функционально полных наборов:
1) F2 и F11; 2) F13 и F8; 3) F9 и F15.
При желании всю алгебру логики можно свести к одной функции. Но чаще всего логические функции записываются в виде логического выражения через инверсию, конъюнкцию и дизъюнкцию.
Введенные пять логических операций дают возможность из простых высказываний строить сложные. Всякое сложное высказывание принимает значение 1 или 0 в зависимости от значения простых высказываний, из которых оно построено.
Таблицу, показывающую, какие значения принимает сложное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называюттаблицей истинности сложного высказывания. Сложные высказывания часто называютформулами логики высказываний.Для любой формулы алгебры логики достаточно просто построить таблицу истинности.
Доказать что число логических функций двух логических переменных равно 16
Логические элементы и логические функции.
Элементы математической логики.
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.
таблицей, которая называется таблицей истинности.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
Таблица истинности функции повторения имеет вид:
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
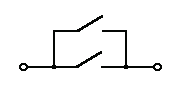
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Таблица истинности логического ИЛИ имеет вид:
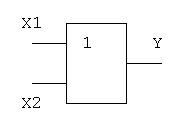
Логический элемент ИЛИ обозначается на схемах следующим образом:
2. Логическое И (логическое умножение, конъюнкция, схема совпаде-
Таблица истинности логического И имеет вид:
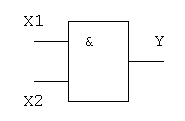
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
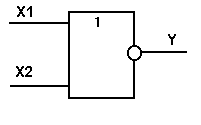
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом :
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)
Таблица истинности функции И-НЕ имеет вид:
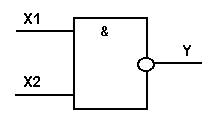
Логический элемент И-НЕ обозначается на схемах следующим образом:
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2). Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
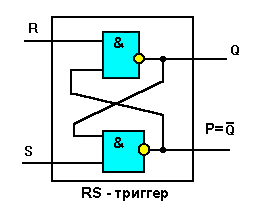
формации. К триггерам относятся устойства, имеющие два устойчивых
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
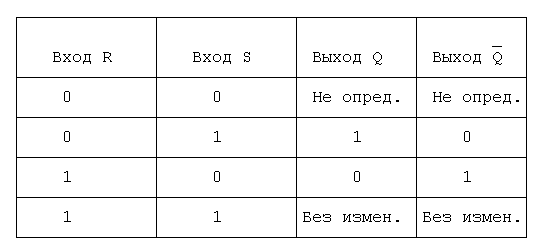
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
В обычном (исходном) состоянии на входы триггера поданы 1. Для
записи информации на вход R подан 0. Для сброса информации и под-
готовки к приёму новой информации на вход S подается 0 и триггер
вернётся в исходное состояние.
Поскольку один триггер запоминает 1 бит информации, то для запо-
минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб
(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо-
собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
формальные математические методы.
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):
Кроме того, применяются ещё три соотношения:
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи
на свойства умножения, поэтому её часто называют логическим умно-
жением. Из законов 6 и 8 следует, что используя отрицание, дизъ-
юнкцию можно выразить через конъюнкцию, и наоборот:
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио-
нально полными или базисными.
1. Что такое логическая функция и логический элемент?
2. Что такое таблица истинности и сколько в ней строк?
3. Какие функции одной переменной Вы знаете? Какая из них являет-
4. Как зависит число функций от числа переменных?
5. Что такое конъюнкция и дизъюнкция? Как они реализуются?
6. Что такое функция стрелка Пирса? Какова её таблица истинности?
7. Что такое функция штрих Шеффера? Какова её таблица истинности?
8. Что такое базисная функция и какие базисы Вы знаете?
9. Что такое логика? Какие два подхода существуют в логике?
10. Как доказывается истинность или ложность высказываний? Приве-
дите примеры из практики.
11. Что такое булева алгебра?
12. Какие законы булевой алгебры Вы знаете? Где они применяются?
13. Что такое триггер? Как работает RS-триггер?
14. Сколько надо триггеров, чтобы запомнить 1 Мб информации?
Логические переменные и логические функции
Вы будете перенаправлены на Автор24
Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции.
Логическая функция может быть задана аналитическим (при помощи формул) или табличным способом.
Логическая функция, представленная с помощью инверсии, дизъюнкции и конъюнкции называется нормальной.
Рисунок 1. Логические функции двух переменных
Готовые работы на аналогичную тему
Среди перечисленных выше шестнадцати логических функций от двух переменных можно выделить такие логические функции, с помощью которых выражаются другие логические функции. Операция замены одной логической функции на другую в алгебре логики (булевой алгебре) называется операцией суперпозиции или метод суперпозиции.
Функцию Шеффера методом суперпозиции можно выразить при помощи функций отрицания и дизъюнкции, используя закон Де Моргана:
Наиболее широко в качестве базовых функций используют три логических функции: конъюнкцию, дизъюнкцию и отрицание. В приведенном примере логическая функция Шеффера выражена через базовые функции и представлена в нормальной форме.
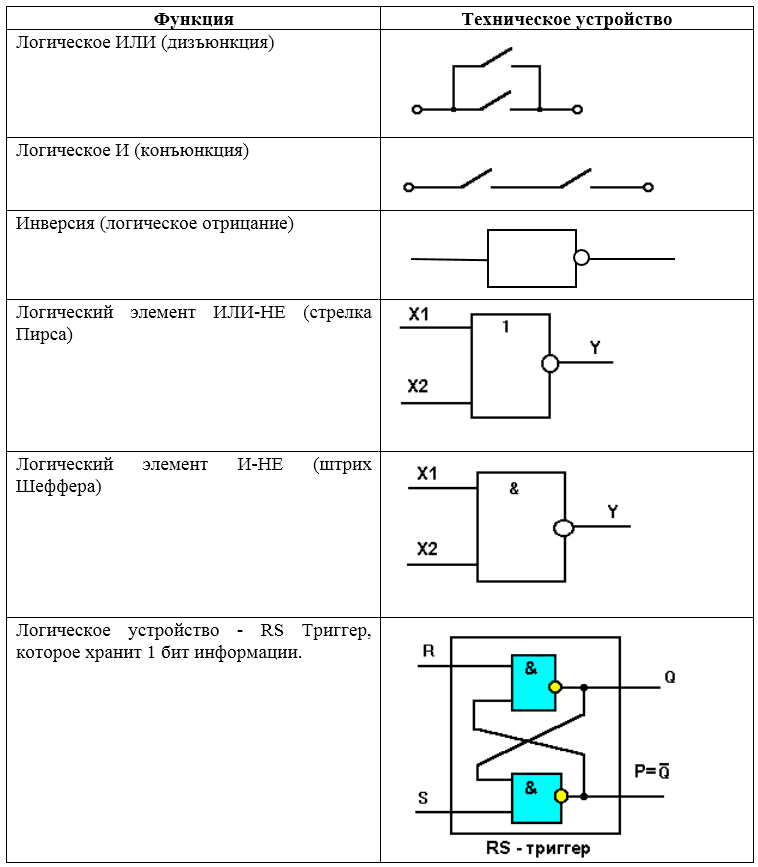
Каждой базовой функции соответствует техническое устройство, реализующее эту логическую функцию.
Рисунок 2. Соответствие базовой функции и технического устройства
Наборы И-НЕ и ИЛИ-НЕ являются функционально полными или базисными наборами.
При помощи набора базовых функций и соответствующих им технических устройств, которые реализуют эти логические функции, создаются любые логические устройства или системы.
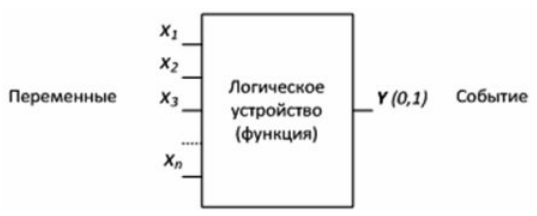
Логическое устройство имеет сколь угодное количество входов и только один выход (См. рис.3).
Рисунок 3. Схематичное представление логического устройства
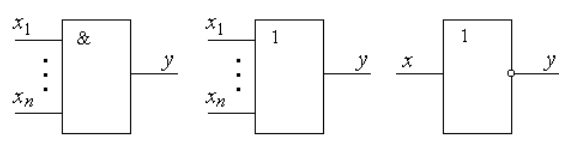
Рисунок 4. Условное обозначение логических элементов на электрических схемах: И (а), ИЛИ (б), НЕ (в)
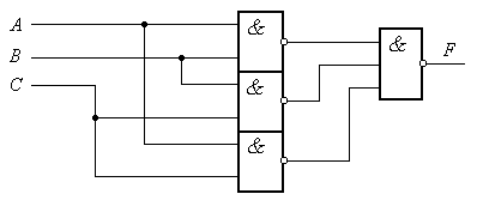
Приведем пример реализации функции при помощи инверсии и отрицания (в базисе И-НЕ).
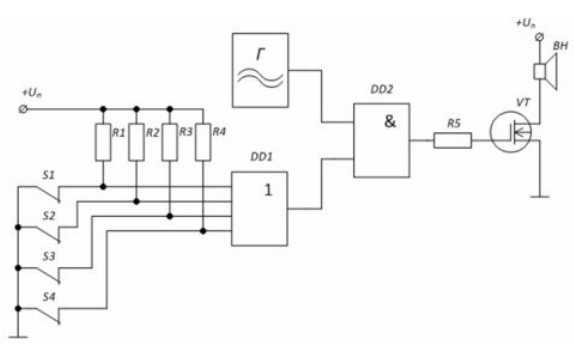
Рисунок 6. Пример схемы охранной сигнализации
История науки и техники Com New
Упражнения для самостоятельного выполнения
1. Выполнить поразрядное логическое сложение и умножение двоичных чисел:
а) 101 и 110; б) 10101 и 11100; в) 110011 и 111100.
2. Преобразовать следующие логические выражения:
3. Доказать, что число логических функций двух логических переменных равно 16.
4. Реализовать модифицированные таблицы истинности логических схем НЕ, ИЛИ, И-НЕ, ИЛИ-НЕ (см. рис. 4.5), используя программу MS Excel.
5. Составить таблицы истинности для следующих логических функций:
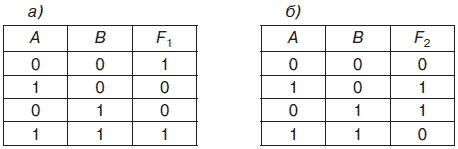
6. Записать выражения для логических функций F и F в виде СДНФ и СКНФ. Логические функции F и F представлены далее соответственно таблицами истинности.
7. По заданному преподавателем варианту таблицы N составить таблицу истинности логической функции F, используя таблицу М. Найти выражение для логической функции F, осуществить ее преобразование в соответствии с основными законами алгебры логики и разработать логическую схему полученной функции с использованием логических схем НЕ, И, ИЛИ. Для графического отображения разработанной логической схемы использовать любой графический редактор.
Логические функции от двух переменных
Логические операции
Будем считать, что уже имеется некоторый запас элементарных высказываний, относительно каждого из которых известно, истинно оно или ложно. В обычной речи мы часто используем слова, называемые логическими связками, — «не», «и», «или», «следует», «влечет», «эквивалентно», «равносильно», «тогда и только тогда, когда. » и т. п.
Примеры сложных высказываний:
В алгебре логики, как и в обычной алгебре, вводится ряд операций. Рассмотрим пять основных логических операций.
1. Логическая операцияконъюнкция (лат. conjunctio — «связываю»):
• в естественном языке соответствует союзами,а,но,хотя;
• иное название:логическое умножение.
Конъюнкция— это логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Это определение распространяется и на случай п высказываний (п > 2, п —целое число). В соответствии с определением правила выполнения действий для операции конъюнкции можно представить в виде истинностной таблицы:
Истина будет лишь в том случае, когда оба человека не лгут.
2. Логическая операциядизъюнкция (лат. disjunctio — «различаю»):
• в естественном языке соответствует союзуили;
• иное название:логическое сложение.
Дизъюнкция — это логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся истинным тогда и только тогда, когда хотя бы одно из двух образующих его высказываний истинно.
Правила действия для операции дизъюнкции можно представить в виде истинностной таблицы:
Выбирая между истиной и ложью, мы останавливаемся на истине.
В отличие от рассмотренной выше операции дизъюнкции можно рассмотреть строгую дизъюнкцию (двойное «или»), которой в естественном языке соответствует связка «либо. либо. »). Суть этой операции ясна из приведенной ниже таблицы:
Данная операция реализует сложение разряда двоичного числа без переноса в старший разряд.
3. Логическая операция импликация (лат. implicatio — «тесно связываю»):
• в естественном языке соответствует оборотуесли. то. ;
• иное название:логическое следование.
Импликация — это логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Таблица истинности импликации:
Из лжи может следовать что угодно, даже истина, но из истины не может следовать ложь.
4. Логическая операция эквиваленция (лат. aequivalens — «равноценное»):
• в естественном языке соответствует оборотам речитогда и только тогда, в том и только в том случае;
• иное название:равнозначность.
Эквиваленция — это логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Эквивалентны ли высказывания, то есть одинаковы ли значения высказываний?
Таблица истинности эквиваленции:
5. Логическая операция инверсия (лат. inversio — «переворачиваю»):
• в естественном языке соответствует словамневерно, что. и частицене;
• обозначение: 
• иное название:отрицание.
Отрицание — это логическая операция, которая каждому данному высказыванию ставит в соответствие новое высказывание, которое истинно, если данное высказывание ложно, и ложно, если данное высказывание истинно.
Таблица истинности инверсии:
| A |  |
Таблицы истинности
Логические функции могут быть заданы табличным способом или аналитически — в виде соответствующих формул.
Истинность или ложность сложных высказываний, образованных в результате выполнения логических операций над простыми высказываниями, не зависит от смыслового содержания исходных высказываний и определяется только их значениями (истинностью или ложностью).
Определим количество различных логических функций с заданным числом переменных п. Логическая функция на каждом наборе переменных принимает значение 0 или 1.
Следовательно, отличающихся друг от друга функций может быть ровно столько, сколько существует различных комбинаций из m = 2 n нулей и единиц.
Логические функции от двух переменных
Пусть п = 2. Существует 16 различных логических функций от двух переменных. Рассмотрим их подробно:
| Аргу-менты | Функции | ||||||||||||||||
| X1 | X2 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | F14 | F15 | F16 |
F3 — отрицательные импликации X1 и X2.
F4 — функция, повторяющая переменная X1.
F7 — строгая дизъюнкция или отрицание эквивалентности
(неравнозначность) переменных X1 и X2. Значение этой функции получается поразрядным сложением двоичных переменных X1 и X2 по модулю 2, то есть без учета переноса в старший разряд.
F9 — отрицание дизъюнкции (функция ИЛИ-НЕ); эта функция называется также функцией Пирса («стрелка» Пирс).
F11 — отрицание переменной X2.
F15 — отрицание конъюнкции (функция И-НЕ); эта функция называется также функцией Шеффера («штрих» Шеффера).
С увеличением числа аргументов количество логических функций резко возрастает. Так, при п = 3 их будет уже 256. Но изучать их все нет никакой необходимости. Дело в том, что функция любого количества переменных может быть выражена через функции только двух переменных. Делается это с помощью приема суперпозиции, состоящего в том, что, во-первых, на место переменных подставляются функции, во-вторых, переменные меняются местами.
Минимальное количество функций двух переменных, через которое можно выразить все другие логические функции, называетсяфункционально полным набором логических функций.
Вот несколько примеров функционально полных наборов:
1) F2 и F11; 2) F13 и F8; 3) F9 и F15.
При желании всю алгебру логики можно свести к одной функции. Но чаще всего логические функции записываются в виде логического выражения через инверсию, конъюнкцию и дизъюнкцию.
Введенные пять логических операций дают возможность из простых высказываний строить сложные. Всякое сложное высказывание принимает значение 1 или 0 в зависимости от значения простых высказываний, из которых оно построено.
Таблицу, показывающую, какие значения принимает сложное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называюттаблицей истинности сложного высказывания. Сложные высказывания часто называютформулами логики высказываний.Для любой формулы алгебры логики достаточно просто построить таблицу истинности.