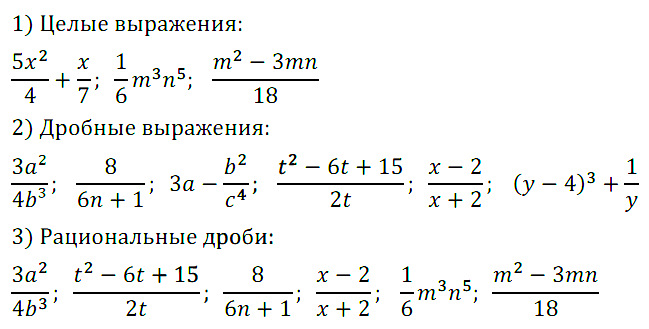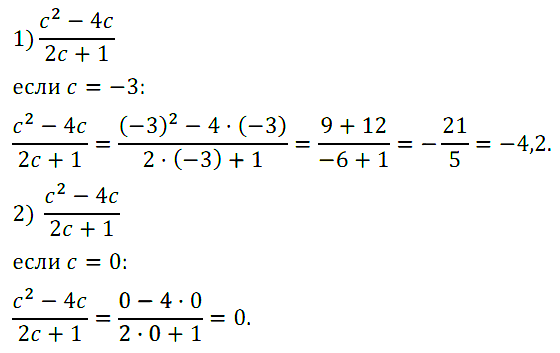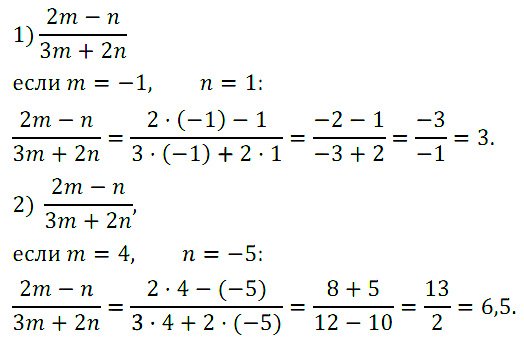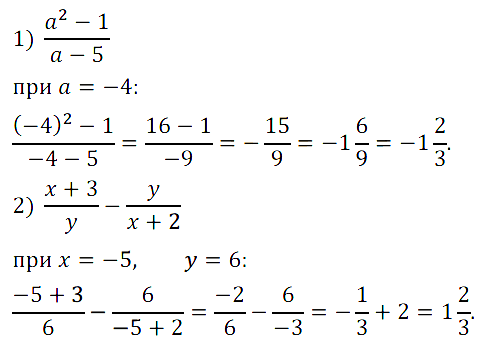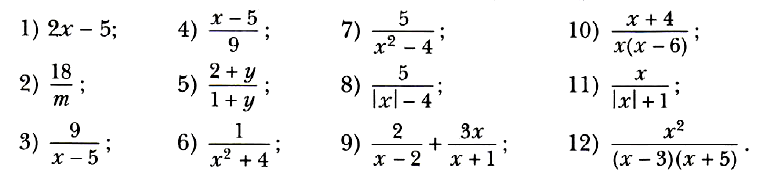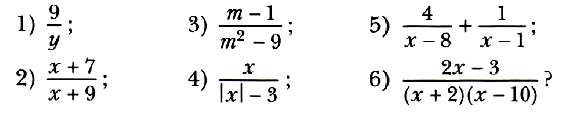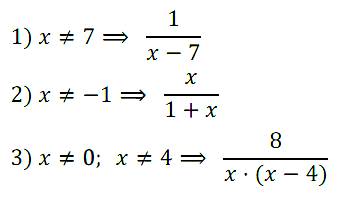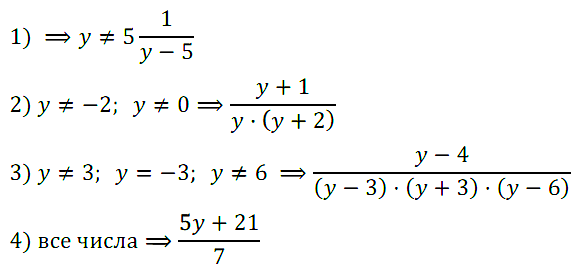Доказать что если 3х5 m2 m4 x то x m
Доказать что если 3х5 m2 m4 x то x m
ВНИМАНИЕ! В связи с новой волной пандемии и шумом вокруг вакцинации агрессивные антивакцинаторы банятся без предупреждения, а их особенно мракобесные комментарии — скрываются.
Основные условия публикации
— Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
— Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
— Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
— Видеоматериалы должны иметь описание.
— Названия должны отражать суть исследования.
— Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
Не принимаются к публикации
— Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
— Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
— Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
— Оскорбления, выраженные лично пользователю или категории пользователей.
— Попытки использовать сообщество для рекламы.
— Многократные попытки публикации материалов, не удовлетворяющих правилам.
— Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает @SupportComunity и общество пикабу.
«Методы решения задач с параметрами»
МКОУ «Лодейнопольская средняя общеобразовательная школа № 68»
Выступление на заседании МО
Методы решения задач
Прокушева Наталья Геннадьевна
Задачи с параметрами
Задачи с параметрами относятся к наиболее сложным из задач, предлагающихся как на Едином государственном экзамене, так и на дополнительных конкурсных экзаменах в ВУЗы.
Они играют важную роль в формировании логического мышления и математической культуры. Затруднения, возникающие при их решении связаны с тем, что каждая задача с параметрами представляет собой целый класс обычных задач, для каждой из которых должно быть получено решение.
Если в уравнении (неравенстве) некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение (неравенство) параметрическим.
Решить уравнение (неравенство) с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они. Два уравнения (неравенства), содержащие одни и те же параметры, называются равносильными, если:
а) они имеют смысл при одних и тех же значениях параметров;
б) каждое решение первого уравнения (неравенства) является решением второго и наоборот.
Естественно, такой небольшой класс задач многим не позволяет усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет «общаться» с параметром как с числом, а во-вторых, – степень свободы общения ограничивается его неизвестностью. Так, деление на выражение, содержащее параметр, извлечение корня четной степени из подобных выражений требуют предварительных исследований. Как правило, результаты этих исследований влияют и на решение, и на ответ.
Как начинать решать такие задачи? Не надо бояться задач с параметрами. Прежде всего, надо сделать то, что делается при решении любого уравнения или неравенства- привести заданное уравнение ( неравенство) к более простому виду, если это возможно: разложить рациональное выражение на множители, разложить тригонометрический многочлен на множители, избавиться от модулей, логарифмов, и т.д.. затем необходимо внимательно еще и еще прочитать задание.
При решении задач, содержащих параметр, встречаются задачи, которые условно можно разделить на два большие класса. В первый класс можно отнести задачи, в которых надо решить неравенство или уравнение при всех возможных значениях параметра. Ко второму классу отнесем задания, в которых надо найти не все возможные решения, а лишь те из них, которые удовлетворяют некоторым дополнительным условиям.
Наиболее понятный для школьников способ решения таких задач состоит в том, что сначала находят все решения, а затем отбирают те, которые удовлетворяют дополнительным условиям. Но это удается не всегда. Встречаются большое количество задач, в которых найти все множество решений невозможно, да нас об этом и не просят. Поэтому приходится искать способ решить поставленную задачу, не имея в распоряжении всего множества решений данного уравнения или неравенства, например, поискать свойства входящих в уравнение функций, которые позволят судить о существовании некоторого множества решений.
Основные типы задач с параметрами
Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.
Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
Обращаем внимание на то, что при решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.
Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).
Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.
Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых:
1) уравнение выполняется для любого значения переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.
Комментарий. Многообразие задач с параметром охватывает весь курс школьной математики (и алгебры, и геометрии), но подавляющая часть из них на выпускных и вступительных экзаменах относится к одному из четырех перечисленных типов, которые по этой причине названы основными.
Наиболее массовый класс задач с параметром — задачи с одной неизвестной и одним параметром. Следующий пункт указывает основные способы решения задач именно этого класса.
Основные методы решения задач с параметром
Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.
Комментарий. По мнению авторов, аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Комментарий. Исключительная наглядность и красота графического способа решения задач с параметром настолько увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать другие способы решения, забывая общеизвестный факт: для любого класса задач их авторы могут сформулировать такую, которая блестяще решается данным способом и с колоссальными трудностями остальными способами. Поэтому на начальной стадии изучения опасно начинать с графических приемов решения задач с параметром.
Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Перейдем теперь к демонстрации указанных способов решения задач с параметром.
1. Линейные уравнения и неравенства с параметрами
Линейная функция: 
– уравнение прямой с угловым коэффициентом 
. Угловой коэффициент равен тангенсу угла наклона прямой к положительному направлению оси 
.
Линейные уравнения с параметрами вида 
Если 
, уравнение имеет единственное решение.
Алгебра 8 класс Мерзляк Упражнения 1-26
Алгебра 8 класс УМК Мерзляк. Упражнения №№ 1 — 26 из учебника с ответами и решениями. Глава 1. Рациональные выражения. § 1. Рациональные дроби. Алгебра 8 Мерзляк Упражнения 1-26 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Алгебра 8 класс Мерзляк
§ 1. Упражнения №№ 1 — 26:
Задание № 2. Чему равно значение дроби (c 2 – 4c)/(2c + 1), если: 1) с = –3; 2) с = 0?
Задание № 3. Найдите значение выражения (2m – n)/(3m + 2n), если: 1) m = –1, n = 1; 2) m = 4, n = –5.
Задание № 4. Чему равно значение выражения: 1) (a 2 – 1)/(a – 5) при а = –4; 2) (х + 3)/у – у/(х + 2) при х = –5, у = 6?
Задание № 5. Найдите допустимые значения переменной, входящей в выражение: 
Задание № 6. При каких значениях переменной имеет смысл выражение: 
Задание № 7. Запишите рациональную дробь, которая содержит переменную х и имеет смысл при всех значениях х, кроме: 1) х = 7; 2) х = –1; 3) х = 0 и х = 4.
Задание № 8. Запишите рациональную дробь, содержащую переменную у, допустимыми значениями которой являются:
1) все числа, кроме 5; 3) все числа, кроме 3, –3 и 6;
2) все числа, кроме –2 и 0; 4) все числа.
Задание № 9. Автомобиль проехал по шоссе а км со скоростью 75 км/ч и по грунтовой дороге b км со скоростью 40 км/ч. За какое время автомобиль проехал весь путь? Составьте выражение и найдите его значение при а = 150, b = 20.
Задание № 10. Ученик купил тетради по 8 р., заплатив за них m р., и по 14 р., заплатив за них n р. Сколько тетрадей купил ученик? Составьте выражение и найдите его значение при m = 24, n = 56.
Задание № 11. Докажите, что при всех допустимых значениях переменной х значение дроби: 1) 1/x 2 положительное; 2) (x 2 + 1)/(6x – 9 – x 2 ) отрицательное.
Доказать что если 3х5 m2 m4 x то x m
1. Окружность, центр которой расположен в первой координатной четверти, касается оси Ox в точке M, пересекает две гиперболы y =
2. Функция f(x;y), определенная на парах действительных чисел, удовлетворяет условиям f(a;a) = 0, f(a;f(b;c)) = f(a;b) + c для любых a, b, c. Найдите f(11;13,6).
3. У Васи есть кубики трех цветов. Он строит из них башню, ставя каждый следующий кубик на предыдущий. Запрещено использовать более 4 кубиков каждого из цветов. Вася заканчивает строить башню, как только в ней окажется по 4 кубиков каких-то двух цветов. Сколько различных башен может построить Вася?
4. В основании треугольной пирамиды DABC лежит равнобедренный остроугольный треугольник ABC (AC=BC). Известно, что CB > AD, а ребро DA перпендикулярно плоскости ABC. Рассматриваются проекции пирамиды DABC на плоскости, содержащие прямую AC. Известно, что наибольшая площадь такой проекции равна 39, наименьшая равна 15, а площадь треугольника ABC равна 36. Найдите объём пирамиды DABC. В ответ запишите квадрат объёма.
7. Медиана AM и высота BH треугольника ABC (H – на стороне AC) пересекаются в точке P. Найдите PH, если AM = BH = 49, MN = 19, где N – точка пересечения продолжения AM с окружностью, описанной около треугольника ABC. В ответ запишите сумму возможных значений PH.
9. Десять неотрицательных чисел таковы, что их сумма равна 4, а сумма их квадратов равна 5,2. Какое наибольшее значение может иметь самое большое из этих чисел?
10. Даны неотрицательные целые числа такие, что 24^a * 6^b * 18^c делится на 6^<100>. Найдите минимальное возможное значение a + b+ c.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение показательных уравнений.
Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Немного теории.
Показательная функция, её свойства и график
7) a n > 1, если a > 1, n > 0
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leqslant 0\), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 x при a > 0 и при 0 x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.