Доказать что логическое выражение является тождественно истинным
ТОЖДЕСТВЕННО ИСТИННЫЕ И ТОЖДЕСТВЕННО ЛОЖНЫЕ ВЫСКАЗЫВАНИЯ
· приоритет логических операций;
· тождественно истинные и тождественно ложные операции;
· основные законы алгебры логики;
· доказательство логических законов;
· простейшие преобразователи информации;
Если сложное высказывание истинно для всех значений входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ИСТИННЫМ или тавтологией (обозначается константой 1).
Все математические, физические и др. законы являются тавтологиями. Например: (а+b) 2 = a 2 + 2ab + b 2
Прогноз погоды на завтра может быть, например, таким: «Дождь будет или дождя не будет». Такое предсказание будет всегда истинным, хотя вряд ли кого устроит. Его математическая запись:
(по закону исключенного третьего всегда должно быть истинным либо суждение, либо его отрицание).
Проверить, является ли сложное высказывание тождественно истинным, можно по таблице истинности.
Если сложное высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется ТОЖДЕСТВЕННО ЛОЖНЫМ (обозначается константой 0 ).
(по закону противоречия: не могут быть одновременно истинны утверждение и его отрицание.)
Если значения сложных высказываний совпадают при всех возможных значениях входящих в них переменных, то такие высказывания называют РАВНОСИЛЬНЫМИ, ТОЖДЕСТВЕННЫМИ, ЭКВИВАЛЕНТНЫМИ
ОСНОВНЫЕ ЗАКОНЫ (РАВНОСИЛЬНОСТИ) АЛГЕБРЫ ЛОГИКИ
· приоритет логических операций;
· тождественно истинные и тождественно ложные операции;
· основные законы алгебры логики;
· доказательство логических законов;
· простейшие преобразователи информации;
При решении логических задач часто приходится упрощать формулы. Упрощение формул в булевой алгебре производится на основе эквивалентных преобразований, опирающихся на основные законы.
1.1. Закон тождества:
— всякая мысль тождественна самой себе, то есть «А есть А», где А – любое высказывание.
2. Закон исключенного третьего:
— в один и тот же момент времени высказывание может быть либо истинным, либо ложным, третьего не дано. Истинно либо А, либо не А.
НАПРИМЕР. «Число 123 либо четное, либо нечетное, третьего не дано».
Закон исключенного третьего не является законом, признаваемым всеми логиками в качестве универсального закона логики. Этот закон применяется там, где познание имеет дело с жесткой ситуацией: либо-либо, истина-ложь. Там же где встречается неопределенность (например, в рассуждениях о будущем), закон исключенного третьего часто не может быть применен.
Рассмотрим следующее высказывание: «Это предложение ложно». Оно не может быть истинным, потому, что оно утверждает, что оно ложно. Но оно не может быть и ложным, потому что тогда оно было бы истинным. Это высказывание не истинно и не ложно, а потому нарушается закон исключенного третьего.
«В одном городе парикмахер стрижет волосы всем жителям, кроме тех, кто стрижет себя сам. Кто стрижет волосы парикмахеру?»
В нашей формальной системе нет возможности ввести такое ссылающееся само на себя истолкование, поэтому мы не можем выразить все возможные мысли и доводы.
3. Закон непротиворечия:
Именно эта формула часто используется при упрощении сложных логических выражений.
Иногда этот закон формулируется так: два противоречащих друг другу высказывания не могут быть одновременно истинными.
ПРИМЕР. Е = «На Марсе есть жизнь и на Марсе жизни нет»
4. Закон двойного отрицания:
— если отрицать дважды некоторое высказывание, то в результате получается исходное высказывание.
НАПРИМЕР: А = «Неверно, что Матроскин не кот»
Алгебра логики
Алгебра логики — раздел математики, изучающий высказывания с точки зрения их логических значений (истинности или ложности) и логических операций над ними.
Иногда ее называют двоичной логикой или булевой алгеброй по имени английского математика Джорджа Буля.
Для удобства записи, используют обозначение результата через F, а логические высказывания через A (X) и B (Y). Так как возможных вариантов значений всего два, их можно обозначить через 0 (ложь, нет, false, no) и 1 (истина, да, true, yes).
Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логическое высказывание
Логическое высказывание — любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Тождественно истинные высказывания (тавтология)
Тождественно истинными называются высказывания, истинные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 1.
В качестве примеров можно привести высказывания, являющиеся разъяснением термина на основе его словообразования (авиабаза — место базирования авиационной техники). Или любое сложное высказывание, смысл которого сводится к формуле А \/ ¬A.
Тождественно ложные высказывания
Тождественно ложными называются высказывания, ложные при любых значениях входящих в него переменных.
Таким образом, такое высказывание всегда равно 0.
Важно, что большинство высказываний сводится к формуле А /\ ¬A.
Эквивалентные высказывания
Эквивалентными (тождественными или равносильными) называются высказывания, значения которых совпадают при любых значениях входящих в него переменных.
Логические операции
Логическое умножение (конъюнкция)
Представляет собой объединение нескольких логических выражений с помощью союза И. При практическом наборе на компьютере часто используют знаки прямого и обратного деления без пробела: /\
Таким образом, все значения должны быть истинными: И первое, И второе, И. При умножении логических операторов мы получим единицу только если все они будут равны единице:
| A | B | F = A & B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для конъюнкции:
Если хотя бы одно значение ложно, то ложно и всё выражение.
Логическое сложение (дизъюнкция)
Представляет собой объединение логических выражений с помощью союза ИЛИ. Если при сложении результат становится больше нуля, то он выражается единицей. При практическом наборе на компьютере часто используют знаки обратного и прямого деления без пробела: \/
| A | B | F = A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Отсюда вытекает обратное следствие, упрощающее вычисления для дизъюнкции:
Если хотя бы одно значение истинно, то истинно и всё выражение.
Логическое отрицание (инверсия)
Представляет собой логическое выражение с добавленной в начале частицей НЕ. То есть операция всегда обращает значение в противоположное.
| A | F = ¬A |
| 0 | 1 |
| 1 | 0 |
Логическое следование (импликация)
Связывает два логических выражения с помощью оборота ЕСЛИ. ТО.
Дополнительная операция, так как A → B = 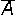
Кроме того, при построении высказывания могут использоваться выражения «из. следует», «. влечет».
| A | B | F = A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В таблице хорошо видна практическая суть: импликация ложна только тогда, когда первое выражение истинно, а второе ложно.
При решении задач, в большинстве случаев требуется применение закона снятия импликации.
Логическое равенство (эквивалентность)
Образуется соединением двух логических выражений с помощью оборотов «тогда и только тогда», «необходимо и достаточно», «. равносильно. ». Поскольку мы видим здесь двойное следование (и вправо и влево), операцию иногда называют двойной импликацией. Дополнительная операция, так как A ↔ B = (A ∨ 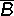
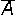
| A | B | F = A ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Суть: эквивалентность ложна только тогда, когда выражения разные.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
| № | Для ИЛИ | Для И | Примечание |
| 1 | A + 0 = A | A • 1 = A | Ничего не меняется при действии, константы удаляются |
| 2 | A + 1 = 1 | A • 0 = 0 | Удаляются переменные, так как их оценивание не имеет смысла |
| 3 | A + B = B + A | AB = BA | Переместительный (коммутативности) |
| 4 | A + 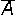 = 1 = 1 | Один из операторов всегда 1 (закон исключения третьего) | |
| 5 | A • 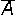 = 0 = 0 | Один из операторов всегда 0 (закон непротиворечия) | |
| 6 | A + A = A | A • A = A | Идемпотентности (NB! Вместо A можно подставить составное выражение!) |
| 7 | ¬¬A = A | Двойное отрицание | |
| 8 | (A+B)+C = A+( B+C) | (A•B)•C = A•(B•C) | Ассоциативный |
| 9 | (A+B)•C = = (A•C)+( B•C) | (A•B)+C = = (A+C)•( B+C) | Дистрибутивный |
| 10 | (A+B)•(¬A+B) = B | (A•B)+(¬A•B) = B | Склеивания |
| 11 | ¬(A+B) = ¬A•¬ B | ¬(A•B) = ¬A+¬ B | Правило де Моргана |
| 12 | A+(A•C) = A | A•(A+C) = A | Поглощение |
| 13 | A→B = ¬A+ B и A→B = ¬B→ ¬A | Снятие (замена) импликации | |
| 14 | 1) A↔B = (A•B)+(¬A•¬ B) 2) A↔B = (A + ¬B)•(¬A + B) | Снятие (замена) эквивалентности | |
Порядок решения логического выражения
В первую очередь надо учитывать, что порядок задается скобками.
Далее выполняются операции отрицания, конъюнкции, дизъюнкции, импликации, эквивалентности.
Построение таблиц истинности
Чтобы решить логическое выражение, необходимо построить таблицу истинности, описывающую ВСЕ возможные варианты значений переменных величин. В связи с тем, что мы используем булевы переменные (то есть имеющие только два значения: 0 и 1), количество вариантов легко сосчитать по формуле
где N — число переменных, а M — число строк в результирующей таблице.
Заполнение же значений фактически является последовательным вписыванием в каждой строке двоичных чисел. Для первой строки это будет 0 (00, 000. ), для второй — 1 (01, 001. ), а для последней — числа, состоящего из всех единиц. Выполнение этого несложного правила позволит не только избежать ошибок, но и облегчит решение, так как значения 0/1 будут подчиняться определенному порядку для каждой переменной.
Графическое решение числовых выражений по координатной прямой
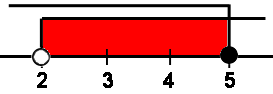
Ряд заданий в алгебре логики основывается в использовании в качестве высказывания числового выражения. Например,
Хорошо видно, что выражение берется в скобки для однозначного восприятия. Прежде чем наносить значения на рисунок, следует избавиться от отрицания. В этом случае происходит замена знаков отношения на противоположные по схеме: ↔ ≤, = ↔ ≠.
В нашем примере мы получим
Нанесем два значения на координатную прямую и, учитывая логическое И, у нас должны совпасть оба условия. То есть на прямой это будет пересечение, обозначенное красным.
Возможные целочисленные ответы — 3, 4, 5.
Построение логического выражения по таблице истинности
Задача является противоположной стандартной.
При ее решении нужно построить дизъюнкцию для всех строк, равных 1, то есть составить выражение в дизъюнктивной нормальной форме (ДНФ).
Решение текстовых задач
На предыдущих этапах, в частности, изучались графический и табличный способы, которые невозможно, либо чрезмерно трудоемко использовать для сложных заданий. Также, решение задач путем рассуждений зачастую неэффективно.
Многие учащиеся очень расстраиваются, что, используя ранее эти способы, они тратили много времени на то, чтобы выработать стратегию, правильно понимать задание и т.п. А теперь их удается решить буквально за несколько секунд. Эта позиция неверна. Большинство подобных задач в реальной жизни не содержит достаточных сведений для решения средствами алгебры логики. Умение анализировать данные и находить «пробелы» в исходных данных — намного важнее.
При решении логической задачи средствами алгебры логики, необходимо выделить из текста логические условия и записать их в виде выражения.
Каждое высказывание оформляется в виде логической переменной. Чаще всего удобно вводить переменные, обозначенные русскими буквами и связанные с объектами, описанными в задаче: Иван — И, красный — К (или Кр, если переменная К уже введена для Коли) и т.п.
В большинстве случаев потребуется упрощение выражения с использованием законов алгебры логики.
В некоторых случаях удобно составить систему высказываний (аналогично системе уравнений) и, затем, решать уже её.
Логическое значение категорически рекомендуется записывать как 0 (ложь) или 1 (истина). Это поможет дифференцировать записи, а не спотыкаться о глупейшие варианты Л/И.
Введем обозначения для логических высказываний:
Л — победит Ласточка; С — победит Стрела; Т — победит Тормоз.
Запишем высказывания (высказывание Петра «Тормоз готовился очень тщательно» не содержит информации о месте и не может быть учтено):
Учитывая истинность предположений двух друзей и ложность третьего, запишем истинное высказывание, основанное на том, что неправ либо первый, либо второй, либо третий:
Затем упростим его за счет двойного отрицания, правила Моргана и убрав ненужные для первого члена скобки:
[¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [(Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С] \/ [(Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С] = 1
Выражение по-прежнему немаленькое. Далее, по закону поглощения можно сократить показанное красным
[ ¬Л /\ С /\ Л /\ ¬Т /\ С] \/ [ (Л \/ ¬С) /\ (¬Л \/ Т) /\ ¬С ] \/ [ (Л \/ ¬С) /\ (Л /\ ¬Т) /\ ¬С ] = 1
[(¬Л \/ Т) /\ ¬С] \/ [(Л /\ ¬Т) /\ ¬С] = 1
В оставшейся части сократим противоположные слагаемые (по закону исключения третьего)
Конечно, можно сразу сказать, что в произведении все три множителя должны быть равны единице, то есть: Л = 1, Т = 0, С = 0. Ответ: победителем скачек стала Ласточка.
Но можно сделать то же, построив таблицу истинности:
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Логические выражения.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§11. Логические выражения.
Формализация
Ключевые слова:
Обозначив простые высказывания буквами — логическими переменными и используя логические операции, можно записать любое высказывание в виде логического выражения.
Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трёх двигателей самолёта. Обозначим высказывания:
А = Первый двигатель вышел из строя;
В = Второй двигатель вышел из строя;
С = Третий двигатель вышел из строя;
X = Аварийная ситуация.
Тогда логическое высказывание X можно записать в виде логического выражения (логической формулы):
X = (А и В) или (А и С) или (В и С).
Это выражение может быть записано с помощью других обозначений:
X = (А • В) + (А • С) + (В • С). (*)
Таким образом, мы выполнили формализацию.
Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
При вычислении логических выражений установлен такой порядок выполнения операций:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Можно ли убрать скобки в выражении (*)? Почему?
Уберите лишние скобки в логических выражениях:
а) X = (А + (В • С) • (А + С));
б) X = (А + B) • (C • А) • (А + (B + C))).
Вычислите значение логического выражения X = (А • В + С) • (А + C) при:
а) А = О, В = О, С = 1;
б) А = О, В = 1, С = 1;
в) А = 1, В = 1, С = 0.
Таблицы истинности
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 2 3 = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
Составление условий
Логические выражения часто используются при решении математических задач с помощью компьютеров.
Построим условия (логические выражения), соответствующие заштрихованным областям на числовой оси (рис. 2.22).
Рис. 2.22
На рисунке 2.22, а выделен отрезок [3; 6]. Для того чтобы определить такую область, нужно ограничить значение х с двух сторон: оно должно быть больше или равно трём и меньше или равно шести, причем эти два условия должны выполняться одновременно, т. е. их нужно связать с помощью операции И:
Область на рис. 2.22, б — это объединение двух отрезков. Мы можем отдельно записать условия для каждого отрезка и связать их с помощью операции ИЛИ:
(1 ≤ х) и (х ≤ 3) или (5 ≤ х) и (х ≤ 8).
Запишите условие, которое определяет область на рис. 2.22, в.
Теперь рассмотрим задачу с областью на плоскости. Запишем условие, соответствующее заштрихованной части (рис. 2.23).
Рис. 2.23
Требуется составить логическое выражение, зависящее от переменных х и у, которое будет равно 1 (истинно) внутри заштрихованной области и равно 0 вне её.
Рис. 2.24
Запишите условие, которое определяет области на рисунках (рис. 2.25).
Рис. 2.25
Построим логическое выражение для области на рис. 2.26.
Рис. 2.26
Можно разделить заштрихованную область на две части (рис. 2.27).
Рис. 2.27Обе области находятся внутри круга радиуса 1 с центром в начале координат, т. е. в области х 2 + у 2 ≤ 1. Первая область описывается выражением
(х 2 + у 2 ≤ 1) и (х ≤ 0),
а вторая — выражением
Поскольку нам нужно «сложить» две области, эти выражения нужно объединить с помощью операции логического сложения (ИЛИ):
Общее условие х 2 + у 2 ≤ 1 можно вынести за скобки:
Попробуйте ещё упростить полученное условие.
Запишите условие, которое определяет области на рисунках (рис. 2.28).
Рис. 2.28
Логические схемы
Вернёмся снова к примеру с системой аварийной сигнализации самолёта. Предположим, что на каждом двигателе установлен логический датчик, который выдаёт условный сигнал 1 (например, высокий уровень напряжения), если двигатель неисправен, и условный сигнал 0, если двигатель исправен. Требуется построить логическую схему — схему логического устройства, — которая при аварии выдаёт условный сигнал 1, а в режиме нормальной работы — сигнал 0.
Сигналы от трёх двигателей назовём А, Б и С. В начале параграфа мы уже составили логическое выражение для запуска аварийной сигнализации:
Х = А • В + А • С + В • С.
Здесь три логических умножения и два логических сложения. Сначала выполняются все операции умножения (слева направо), а затем — все операции сложения (тоже слева направо). Расставим номера операций:
| 1 | 4 | 2 | 5 | 3 | ||||||||
| Х | = | А | • | В | + | А | • | С | + | В | • | С. |
Последней выполняется вторая операция сложения. Поэтому последний элемент в схеме — это элемент логического сложения ИЛИ (рис. 2.29).
Рис. 2.29
На первый вход этого элемента ИЛИ подаётся сигнал А • В + А • С, в этом выражении последняя операция — логическое сложение, добавляем ещё один элемент ИЛИ (рис. 2.30).
Рис. 2.30
Три операции логического умножения добавляют в схему три элемента И (рис. 2.31).
Рис. 2.31
Запишите в тетради логическое выражение по логической схеме (рис. 2.32).
Рис. 2.32
Постройте логическую схему, соответствующую выражению:
в) Z = A • B + A • B • C.
Работа в парах. Один из вас пусть нарисует логическую схему для выражения X = A + В • С (черта сверху обозначает, что операция отрицания применяется ко всему выражению), а второй — для выражения Y = (А + В) (А + С). Постройте таблицы истинности для своих выражений и сравните их. Какую формулу вы сейчас вместе доказали?
Работа в парах. Запишите логическое выражение, включающее 5-6 операций, и предложите соседу нарисовать логическую схему. Проверьте и обсудите с ним его решение.
Путешествуя по Зазеркалью, Алиса увидела дверь с тремя кнопками, которые были отмечены буквами А, В и С. На двери висела схема (рис. 2.33).
Рис. 2.33
На какую (одну!) из трёх кнопок нужно нажать Алисе, чтобы открыть дверь?
Выводы
• Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
• В логических выражениях операции выполняются в следующем порядке:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Для изменения порядка действий используются скобки.
• Таблица истинности логического выражения показывает, чему равно значение выражения при всех возможных комбинациях значений исходных переменных.
• Логические выражения, истинность которых зависит от значений исходных переменных, называют вычислимыми.
• Логическое выражение, которое всегда истинно, называется тождественно истинным или тавтологией. Выражение, которое всегда ложно, называют тождественно ложным или противоречием. Пример тождественно истинного выражения: А + А, пример тождественно ложного: А • А.
• Два выражения, принимающие одинаковые значения при всех значениях переменных, называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Что можно сделать для того, чтобы изменить порядок выполнения действий в логических выражениях?
2. Поясните разницу между терминами «логическое выражение» и «логическая функция».
3. Как можно доказать (или опровергнуть) логическую формулу?
4. Можно ли сказать, что таблица истинности однозначно определяет:
а) логическое выражение;
б) логическую функцию?
5. Что такое вычислимое логическое выражение?
6. Что такое равносильные выражения?
7. Выполните по указанию учителя задания в рабочей тетради.