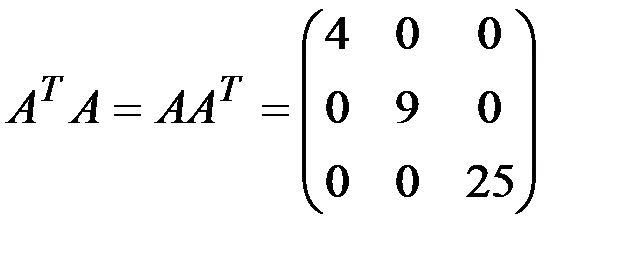Доказать что матрицы а и в коммутирующие
Насколько я понял, все элементы такой матрицы, кроме диагональных, должны быть равны нулю, но я не совсем понимаю, как это оформлять, возникают трудности.
задан 24 Сен ’14 12:29
Leva319
1.7k ● 1 ● 19 ● 100
77% принятых
2 ответа
Добавление. Для иллюстрации:
отвечен 24 Сен ’14 15:20
Что такое базис в линейном пространстве матриц?
Почему Еij * Ekm = 0? Ведь такое произведение определенно только когда j = k.
Имеется в виду, что МАТРИЦУ* можно однозначно представить в виде суммы матричных единиц с коэффициентами
Какую матрицу? Произвольную? Если да, то почему это так? Ведь складывая матричные единицы, помноженные на какие угодно коэффициенты, мы получим матрицу, у которой ненулевые элементы будут в диагонали, и то не всегда.
Аааааааааа, понял, я просто перепутал матричные единицы и единичную матрицу.
@Leva319: вот, я «хотел как лучше», то есть ввёл один из терминов, который часто употребляется в этом контексте. Можно было бы его не использовать, а ограничиться обозначениями. Я не думал, что может возникнуть такого рода путаница: у меня эти два понятия находятся в разных «уголках» сознания. Тем более, что матричных единиц много ($%n^2$%), а единичная матрица всего одна. При этом «получилось как всегда», как любил говорить мой тёзка 🙂
Итак, спасибо, я уловил, что ЛЮБУЮ матрицу можно представить в виде суммы матричных единиц, помноженных на какие-то коэффициенты, это я понял.
Поэтому необходимо и достаточно описать матрицы, коммутирующие с каждым таким базисным элементом.
Т.е. если какая-то матрица коммутирует с каждым элементом представления А через сумму матричных единиц, то она коммутирует и с А? Почему это верно?
Это ещё одно совершенно общее и простое соображение. Если матрица A коммутирует со всеми матрицами, то она коммутирует и с матричными единицами, как частный случай. Обратно: если она коммутирует с матричными единицами, то она коммутирует со всеми линейными комбинациями таких матриц, а это все матрицы.
На самом деле, можно это не анализировать, так как в качестве необходимого условия коммутирования получаются скалярные матрицы, а они пропорциональны единичной, и этого достаточно для коммутирования с чем угодно.
Уважаемый Falcao, спасибо за решения, но вопросы остаются. Вот, логика решения такой, какой я ее понял
Правильно ли я все понял?
отвечен 25 Сен ’14 0:45
Нет, это не совсем точно. Во-первых, не надо всё-таки путать матричные единицы (их много) и единичную матрицу (она для данного размера одна). Во вторых, про матрицу не говорят, что она коммутативна чему-то. Принято говорить, что она коммутирует с чем-то. Это разные термины.
Здравствуйте
Коммутируют ли матрицы
Доказать, что элементы x и y коммутируют
Пусть G — группа. Пусть x, y ∈ G — это такие элементы, что справедливо xy = z ∈ Z(G), где.
Коммутируют ли матрицы?
Помогите не понимаю задание вместо N и M тройки

В целочисленной матрице А(3,4) найти m-количество положительных элементов, стоящих в четных.
Решение
Igor, на самом деле в условиях вашей задачи (при условии самосопряженности матриц), выполняется более сильное условие: для любой непрерывной на спектре функции f
Eugeniy, с приездом! 🙂

1.Дана квадратная матрица A(nхn). Построить вектор b, где bi, i=1,…,n – сумма элементов i-ого.

1.Написать программу с использование собственного модуля, который должен содержать процедуру ввода.
Реализовать умножение матрицы, транспонирование матрицы, обращение матрицы
Реализовать умножение матрицы, транспонирование матрицы, (функция должна быть универсальной).
Проверить коммутируют ли матрицы
Свойства операции сложения матриц
Для любых матриц А, В и С одного размера выполняются равенства:
1. А+В=В+А (коммутативность);
Произведением матрицы А = (aij) на число l называется матрица В = (bij) того же размера, что и матрица А, причем bij=l aij, «i,j.
Свойства операции умножения матрицы на число
2. l(А+В)=lА+lВ (дистрибутивность относительно сложения матриц).
3. (l+m)А=lА+mА (дистрибутивность относительно сложения чисел).
Произведением АВ матриц А и В (размеров m´n и n´r соответственно) называется матрица С размера m´r, такая, что сij= ai1 b1j+ a12 b2j+…+ aik bkj+…+ ain bnj= 
Таким образом, каждый элемент сij, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
Получение элемента сij схематично изображается так
Произведение АВ существует, только если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц
1. (АВ)С=А(ВС)=АВС (ассоциативность).
2. (А+В)С=АС+ВС (дистрибутивность).
3. А(В+С)=АВ+АС (дистрибутивность).
4. АВ¹ВА (отсутствует коммутативность).
Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной (обозначается А Т ).
1.3.1. Найти линейные комбинации заданных матриц:
а) А-lЕ, 
б) 4А-5В, 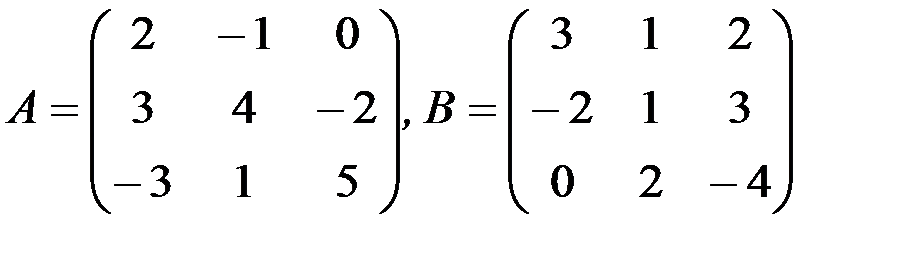
1.3.2. Найти произведения матриц АВ и ВА (если они существуют):
в) 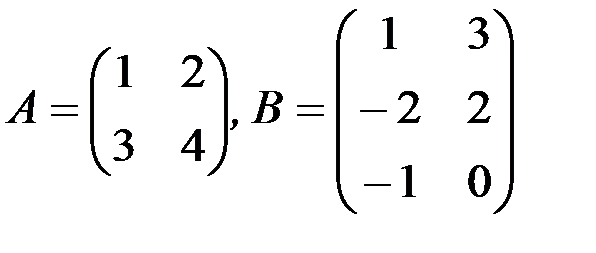
1.3.3. Проверить, коммутируют ли матрицы:
а) 
б) 
1.3.4. Найти произведения матриц АА Т и А Т А:
а) 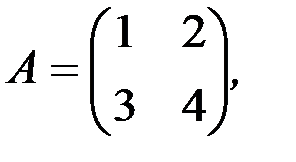
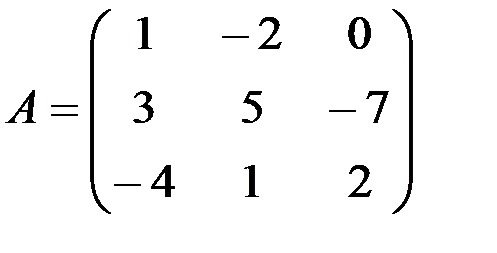
1.3.5. Найти линейные комбинации матриц:
а) 5А-3В+2С, 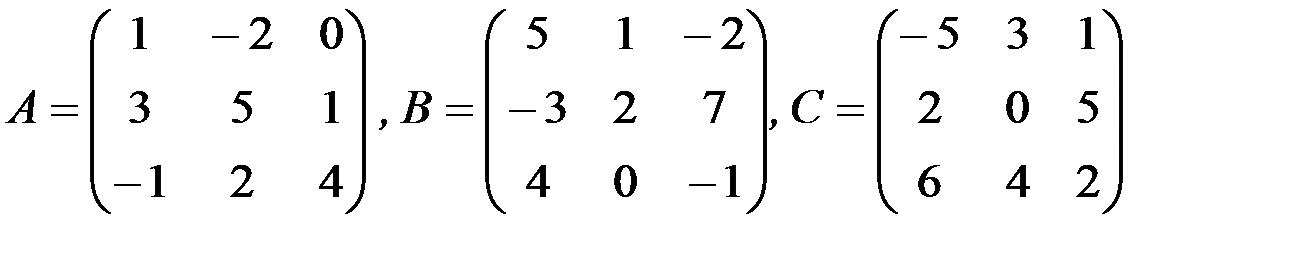
б) А-lЕ, 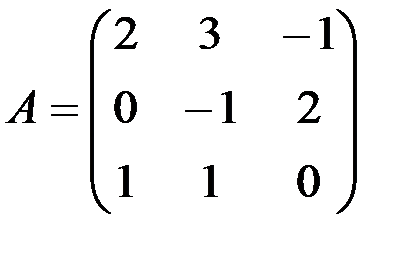
1.3.6. Найти произведения АВ и ВА (если это возможно):
а) 

1.3.7. Найти произведения АА Т и А Т А:
а) 
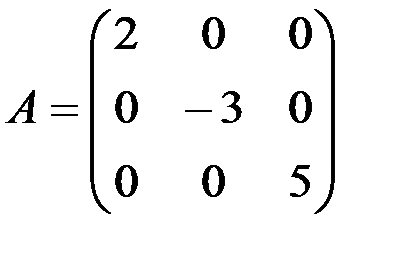
Ответы:
1.3.1.а) 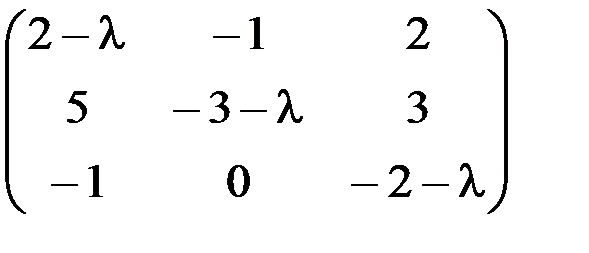
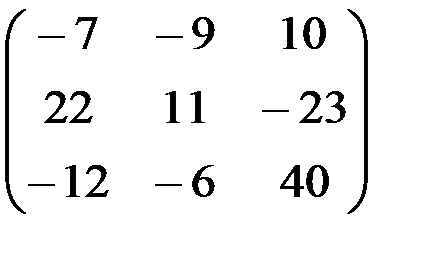
1.3.2.а) 
б) АВ=(31); 
в) АВ не существует, 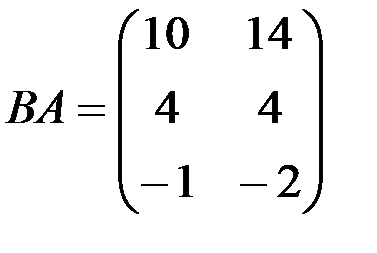
1.3.4.а) 
б) АА Т =(30); 
в) 
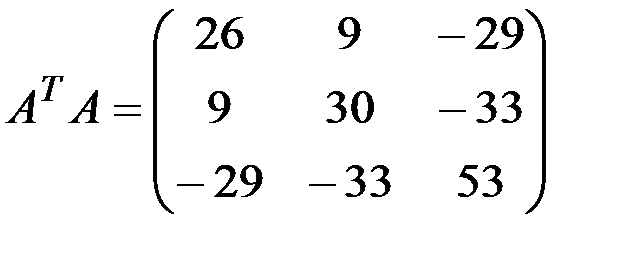
1.3.5.а) 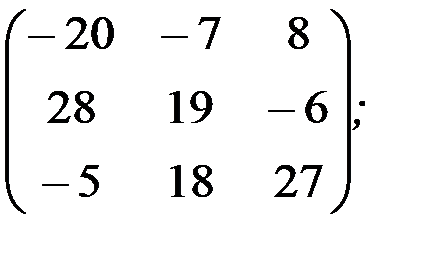
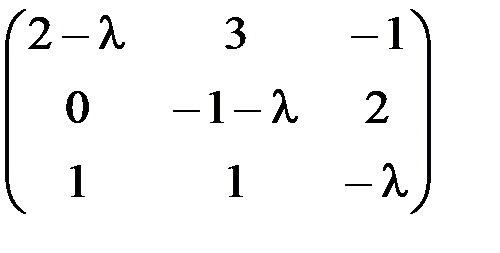
1.3.6.а) 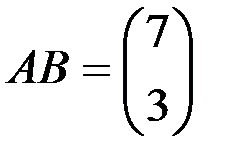
б) 
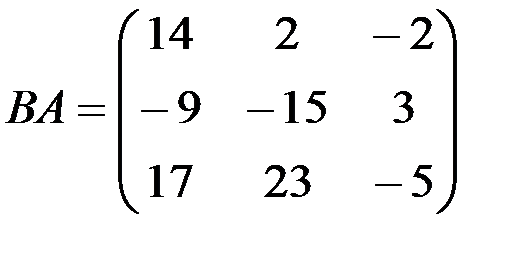
1.3.7.а) 
б) 
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8546 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Ответы на вопрос
1) 18*15=270 (кв.см) – площади
2) 270/27=10 (см) – ширина второго
просто надо чтобы все 3 луча пересеклись в одной точке вот и
60*35=2100м площадь огорода
2100: 12*5=875м занимают огурцы и помидоры
2100-875=1225м занимает картошка.
пусть х тенге- было у него денег.
– столько денег у него осталось.
делим обе части на 2. выходит:
175 тенге было у него)
Похожие вопросы
Вопросы по предметам
Используя этот сайт, Вы даете согласие на использование cookies. Вы можете отказаться от использования cookies, настроив необходимые параметры в своем браузере.
Ответы на вопрос
купили 32 синих карандаша и 16 красных, по одинаковой цене, заплатив за них 96 руб. найти, сколько заплатили за синие карандаши и сколько за красные?
32+16=48 всего карандашей,
96/48=2 руб – один карандаш,
32*2=64 руб – заплатилиза синие карандаши,
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Найти все матрицы n*n,коммутирующие с любой другой матр. n*n
| Заслуженный участник |
Последний раз редактировалось Otta 01.07.2013, 12:39, всего редактировалось 1 раз.
| Заслуженный участник |
Операции над матрицами



Свойства операции сложения матриц
Для любых матриц А, В и С одного размера выполняются равенства:
1. А+В=В+А (коммутативность);
Произведением матрицы А = (aij) на число l называется матрица В = (bij) того же размера, что и матрица А, причем bij=l aij, «i,j.
Свойства операции умножения матрицы на число
2. l(А+В)=lА+lВ (дистрибутивность относительно сложения матриц).
3. (l+m)А=lА+mА (дистрибутивность относительно сложения чисел).
Произведением АВ матриц А и В (размеров m´n и n´r соответственно) называется матрица С размера m´r, такая, что сij= ai1 b1j+ a12 b2j+…+ aik bkj+…+ ain bnj= 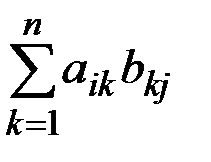
Таким образом, каждый элемент сij, находящийся в i-й строке и j-м столбце матрицы С, равен сумме произведений соответствующих элементов i-й строки матрицы А и j-го столбца матрицы В.
Получение элемента сij схематично изображается так
Произведение АВ существует, только если число столбцов матрицы А равно числу строк матрицы В.
Свойства операции умножения матриц
1. (АВ)С=А(ВС)=АВС (ассоциативность).
2. (А+В)С=АС+ВС (дистрибутивность).
3. А(В+С)=АВ+АС (дистрибутивность).
4. АВ¹ВА (отсутствует коммутативность).
Коммутирующими (или перестановочными) называются матрицы А и В, для которых АВ=ВА.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной к данной (обозначается А Т ).
1.3.1. Найти линейные комбинации заданных матриц:
а) А-lЕ, 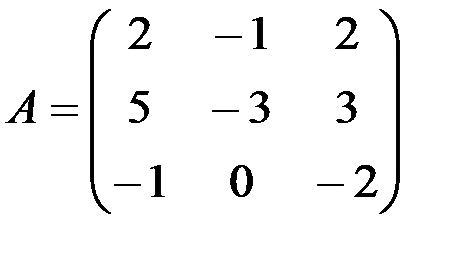
б) 4А-5В, 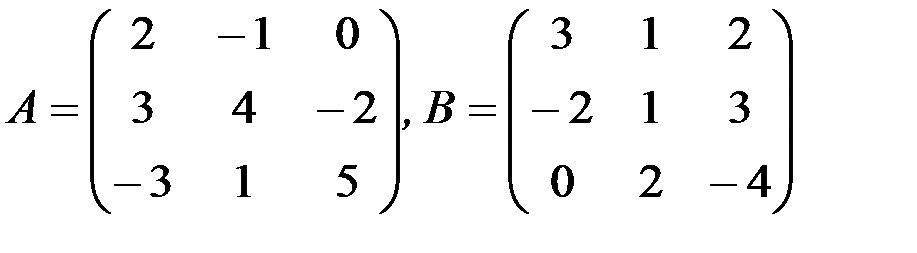
1.3.2. Найти произведения матриц АВ и ВА (если они существуют):
в) 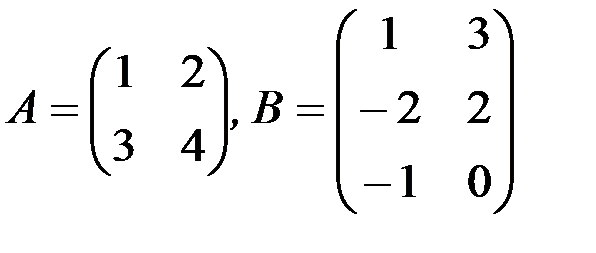
1.3.3. Проверить, коммутируют ли матрицы:
а) 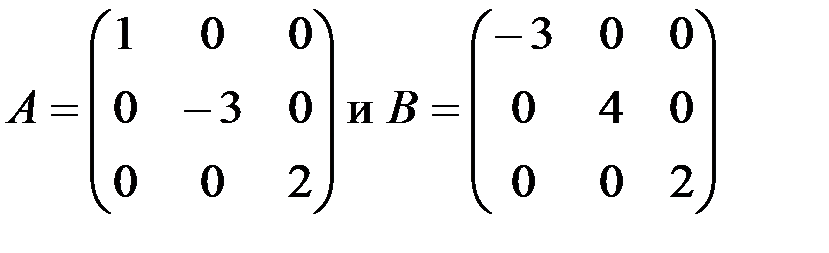
б) 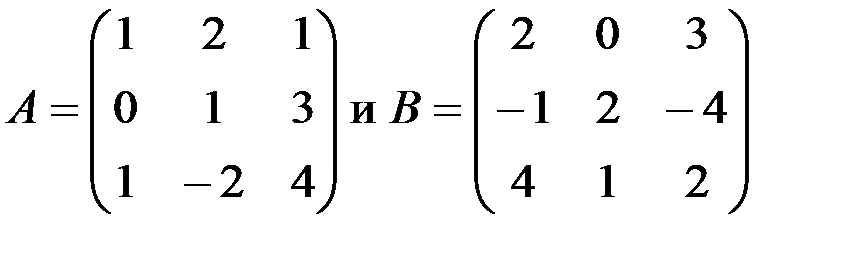
1.3.4. Найти произведения матриц АА Т и А Т А:
а) 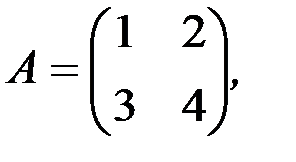
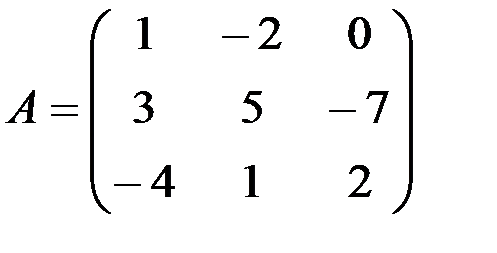
1.3.5. Найти линейные комбинации матриц:
а) 5А-3В+2С, 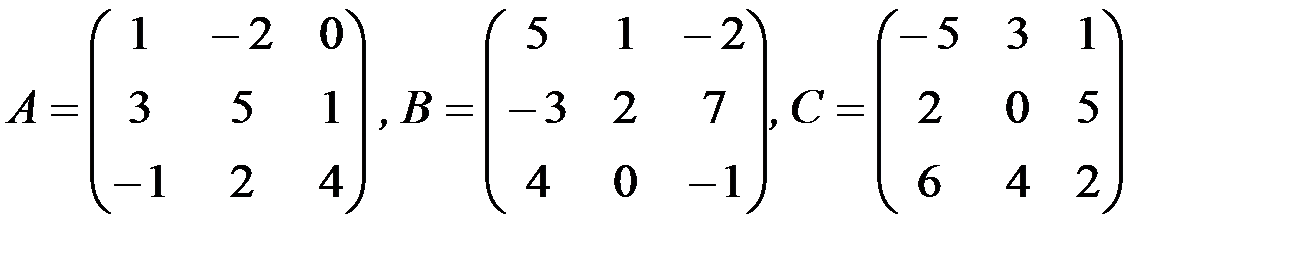
б) А-lЕ, 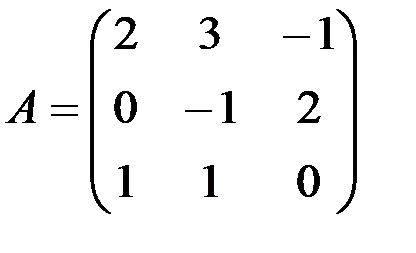
1.3.6. Найти произведения АВ и ВА (если это возможно):
а) 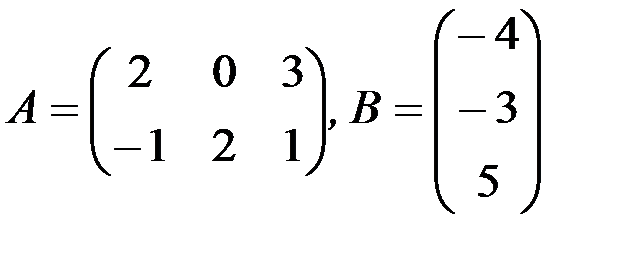
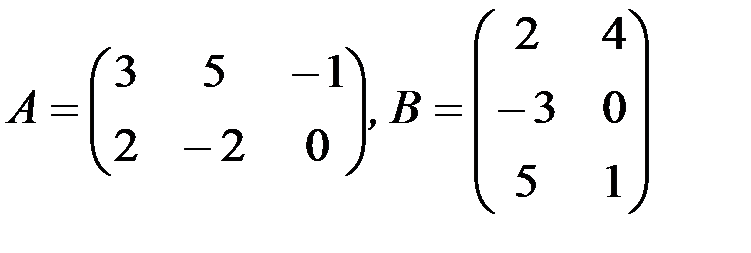
1.3.7. Найти произведения АА Т и А Т А:
а) 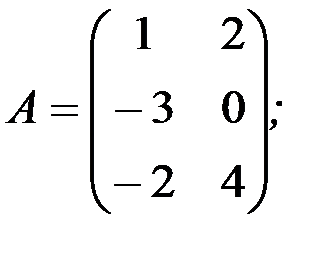
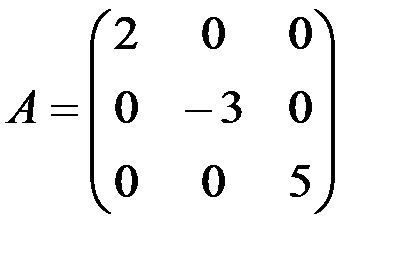
Ответы:
1.3.1.а) 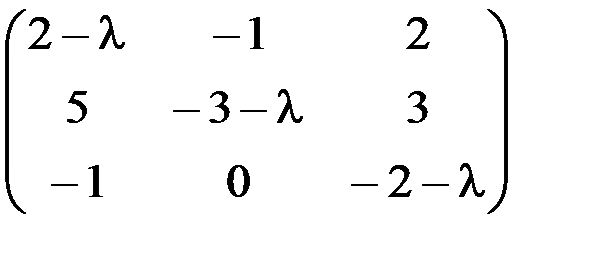
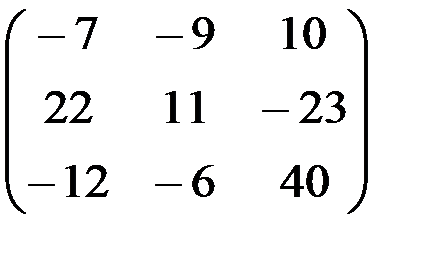
1.3.2.а) 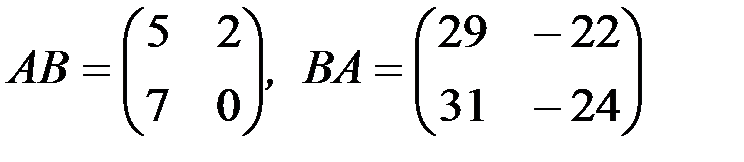
б) АВ=(31); 
в) АВ не существует, 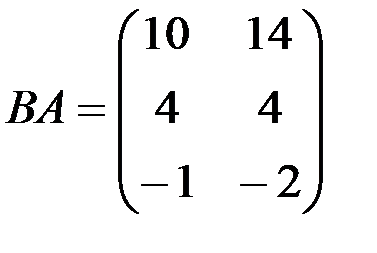
1.3.4.а) 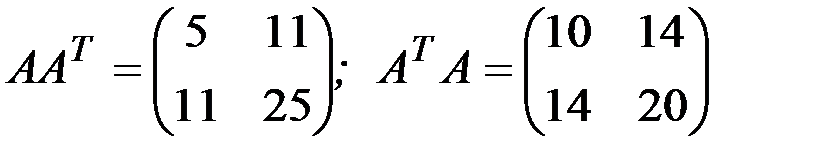
б) АА Т =(30); 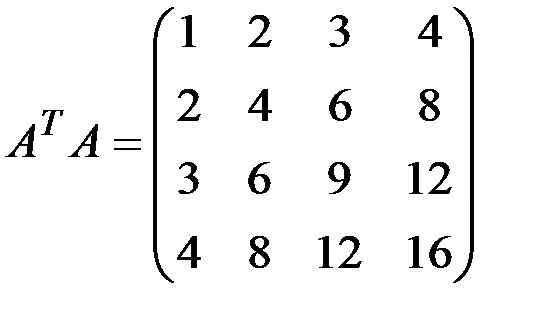
в) 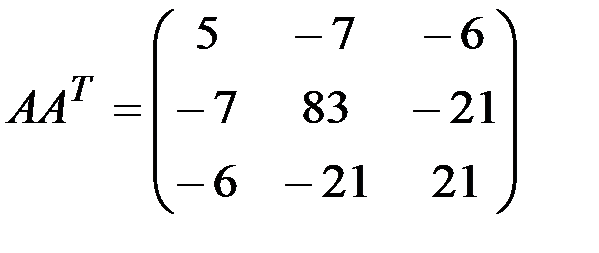
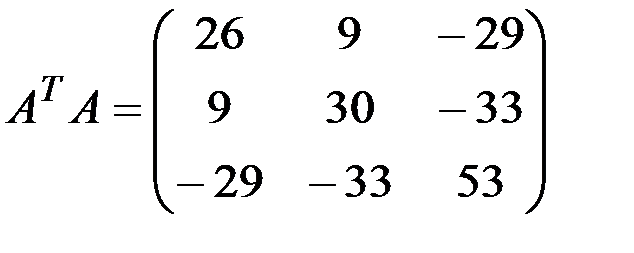
1.3.5.а) 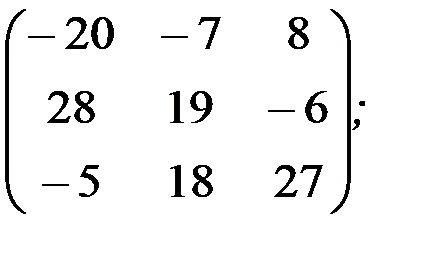
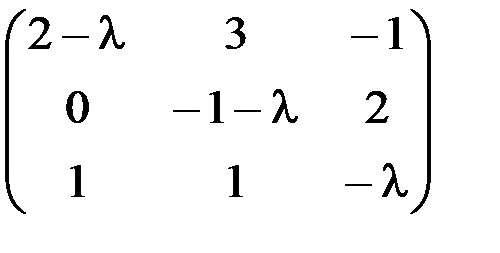
1.3.6.а) 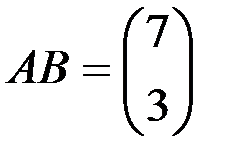
б) 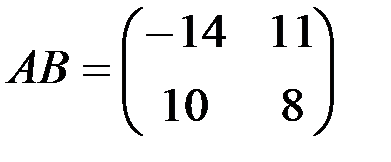
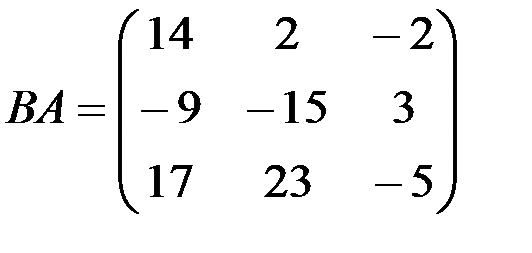
1.3.7.а) 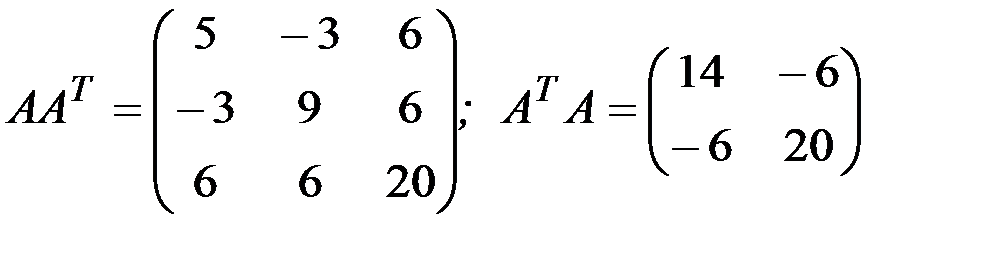
б)