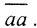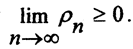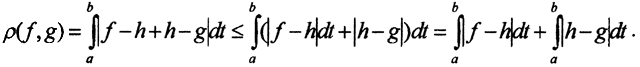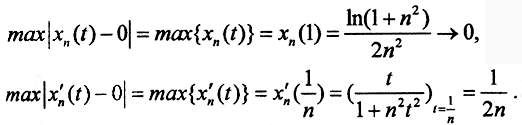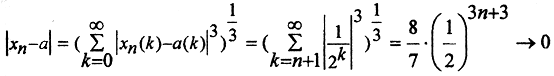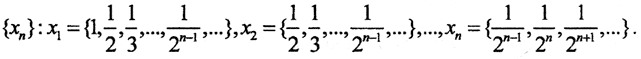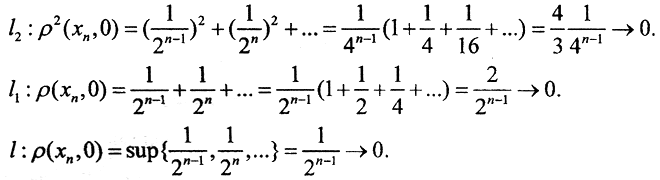Доказать что метрическое пространство полное

II. Основные теоремы о пространствах

2.1. Полные метрические пространства

Теорема 1 (Критерий полноты Кантора). Метрическое пространство полно, если и только если любая последовательность непустых вложенных замкнутых шаров, радиусы которых стремятся к нулю, имеет непустое пересечение.

Необходимость. Пусть последовательность вложенных шаров при r_{n →∞}→0 и пространство (X,ρ) полное. Тогда существует и единственна точка x₀, принадлежащая всем шарам сразу. Рассмотрим последовательность n> центров этих шаров и оценим расстояние ρ(x_n,x_m) при m>n. Так как при , но по условию теоремы r_n→0, стало быть и ρ(x_n,x_m)→0 при n,m→∞. То есть последовательность n> фундаментальна и в силу полноты пространства сходится. Члены её, начиная с m-го, принадлежат шару так как шар замкнутый, то и предел принадлежит этому шару, а то есть пересечение шаров не пусто.

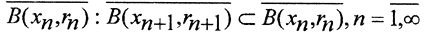
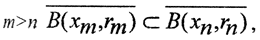
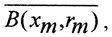
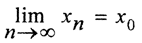
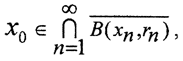
Пример. Может ли в банаховом пространстве иметь пустое пересечение последовательность непустых вложенных замкнутых множеств?

Да, может. Рассмотрим банахово пространство вещественных чисел R и последовательность непустых замкнутых вложенных множеств в нем x_i = [i,∞), i=1,∞. Ясно, что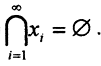

Пример. Множество рациональных чисел есть множество I категории.

Теорема 2 (Теорема Бэра о категориях). Носитель X полного метрического пространства (X,ρ) есть множество II категории.

( Комментарий. Ясно, что в полном метрическом пространстве всякое не пустое открытое множество есть множество второй категории, а множества, дополнительные к множествам первой категории, тоже множества второй категории.)

Определение 2. Полное метрическое пространство (Y,ρ_y) называется пополнением метрического пространства (X,ρ_x), если пространство (X,ρ_x) всюду плотно в пространстве (Y,ρ_y).

Определение 3. Пространства (X,ρ_x) и (Y,ρ_y) называют изомерными, если между ними существует хоть одна биекция и ρ_y = ρ_x.

Теорема 3 (Теорема Хаусдорфа о пополнении метрических пространств). Любое неполное метрическое пространство (X,ρ_x) имеет единственное с точностью до изомерности пополнение.

1. Из элементов данного неполного метрического пространства (X,ρ_x) построим некоторое пространство (Y,ρ_y).

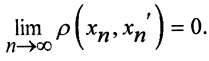
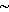
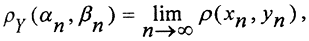
Фундаментальные последовательности n> и n> метрического пространства (X,ρ) назовём конфинальными, если Конфинальность определяет отношение эквивалентности x_nx’_n, то есть это отношение рефлексивно, симметрично и транзитивно. Рефлексивность и симметричность очевидны, а из неравенства треугольника следует транзитивность. Действительно, пусть x_nx’_n, а x’_nx»_n. Тогда ρ(x_n,x»_n)≤ρ(x_n,x’_n)+ρ(x’_n,x»_n). Если ρ(x_n,x’_n)→0 и ρ(x’_n,x»_n)→0, то ρ(x_n,x»_n)→0. Отношение эквивалентности разбивает фундаментальные последовательности пространства (X,ρ_x) на непересекающиеся классы эквивалентных между собой последовательностей. Таким образом мы получили новое фактор-множество Y, элементами которого являются непересекающиеся классы фундаментальных последовательностей <α_n>, <β_n>, <γ_n>. представителями которых являются фундаментальные последовательности n>, n>, n>. пространства (X,ρ_x). Если фундаментальная последовательность n> сходится к точке x, то и эквивалентная ей последовательность <α_n> сходится к той же точке. Действительно, пусть ρ(x_n,x)|_n→∞→0. Тогда ρ(α_n,x)≤ρ(α_n,x_n)+ρ(x_n,x)→0 и ρ(α_n,x)|_n→∞→0. Будем рассматривать фактор-множество Y как носитель нового метрического пространства (Y,ρ_y) с метрикой , если, конечно, удастся доказать, что это метрика.

2.1. Существование. Достаточно показать, что последовательность <ρ_n(x_n,y_n)> фундаментальна, тогда, в силу полноты числовой оси, она сходится. Полнота числовой оси доказывается независимо.

Лемма 1 (О четырёх точках). Для любых четырёх точек x,x’,y,y’ метрического пространства Х справедливо неравенство |ρ(x,y)-ρ(x’,y’)|≤ρ(x,x’)+ρ(y,y’).

ρ(x,y)≤ρ(x,x’)+ρ(x’,y)≤ρ(x,x’)+ρ(x’,y’)+ρ(y’,y) ⇒ ρ(x,y)-ρ(x’,y’)≤ρ(x,x’)+ρ(y,y’). Поменяв местами x,y и x’,y’, получим ρ(x’,y’)-ρ(x,y)≤ρ(x’,x)+ρ(y’,y).

Отсюда сразу |ρ(x,y)-ρ(x’,y’)|≤ρ(x,x’)+ρ(y,y’).

Лемма 2 (О непрерывности метрики). Метрика ρ(x,y) является непрерывной функцией своих аргументов.

Из леммы 1 |ρ(x_n,y_n)-ρ(x,y)|≤ρ(x_n,x)+ρ(y_n,y)→0 при n→∞, то есть если ρ(x_n,x)→0 и ρ(y_n,y)→0 при n→∞, то ρ(x_n,y_n)→ρ(x,y).

Доказательство существования метрического пространства (Y,ρ_y).

Если последовательности n> и n> фундаментальные, то ρ(x_n,x_m)→0 и ρ(y_n,y_m)→0 при m,n→∞. Тогда согласно лемме о четырёх точках можно записать соотношение: |ρ(x_n,y_n)-ρ(x_m,y_m)|≤ρ(x_n,x_m)+ρ(y_n,y_m)→0 при m,n→∞. То есть числовая последовательность <ρ_n(x_n,y_n)> фундаментальна и, следовательно, и сходится в полном пространстве R 1 ₁.

2.2. Доказательство независимости от выбора представителей.

2.3. Проверим выполнение аксиом метрики.

1. По свойствам пределов, связанных с неравенствами, если все члены последовательности <ρ_n(x_n,y_n)>≥0, то и

2. Симметричность очевидна.

3. Докажем аксиому треугольника. Так как ∀ n ρ(x_n,y_n)≤ρ(x_n,z_n)+ρ(z_n,y_n), то, по свойствам пределов, связанных с неравенствами и непрерывности метрики сразу получаем что и третья аксиома справедлива. Таким образом, пространство (Y,ρ_y) метрическое.

3. Покажем, что метрическое пространство (Y,ρ_y) и есть пополнение метрического пространства (X,ρ_x).

Надо показать, что: метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y) и эти пространства изомерны.

3.1. Покажем, что метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y).

3.2. Покажем, что метрическое пространство (Y,ρ_y) полно.

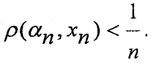
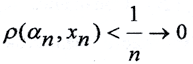
Рассмотрим некоторую фундаментальную последовательность <α_n>∈Y. Так как пространство (X,ρ_X) всюду плотно в (Y,ρ_y), то для каждого номера n найдётся элемент x_n∈X такой, что Тогда из неравенства треугольника следует соотношение ρ(x_n,x_m)≤ρ(x_n,α_n)+ρα_n,x_m) 1 ₁, то есть ρ_y(α₀,x_n)→0. Таким образом, метрическое пространство (Y,ρ_Y) полно.

3.3. Покажем, что метрическое пространство (Y,ρ_Y) является единственным с точностью до изоморфизма пополнением метрического пространства (X,ρ_X).

Источник

Доказать что метрическое пространство полное

1.4.4. Сходимость и полнота в метрических пространствах

Определение 1.Последовательность точек x_n метрического пространства сходится по метрике ρ к точке x, если числовая последовательность ρ(x_n,x)|_n→∞→0, то есть ∀ε&362;0 ∃N=N(ε):(n>N⇒ρ(x_n,x) Комментарий. Обозначение используется обычное: n>→x. Таким образом, в метрических пространствах можно использовать теорию числовых последовательностей с естественной метрикой числовой оси ρ(x,y) = |x-y|. Например:)

Теорема 1. Последовательность точек метрического пространства может иметь только один предел.

Пусть последовательность n> имеет два предела, то есть ρ(x_n,a)|_n→∞→0 и ρ(x_n,b)|_n→∞→0. Тогда в неравенстве треугольника для точек a и b, где a ≠b, ρ(a,b) ≤ρ(a,x_n)+ρ(b,x_n). Правая часть стремится к нулю, а левая часть постоянна и отлична от нуля.

Определение 2. Сходимость по норме (метрике) пространства C[a,b] называется равномерной сходимостью. Сходимость по (метрике) норме пространства L₂[a,b] называется сходимостью в среднем.

Определение 3. Последовательность точек x₁, x₂, x₃. пространства (Х,ρ) называется фундаментальной, если для любого числа ε>0 найдется такое число n₀, что для всех n, m > n₀ выполняется неравенство ρ(x_m, x_n) Комментарий. Ясно, что всякая сходящаяся последовательность является фундаментальной.)

Определение 4. Метрическое пространство, в котором всякая фундаментальная последовательность сходится, называется полным.

( Комментарий. Все стандартные метрические пространства, кроме C_p[a,b], полны, а так как они ещё и нормированы, то все стандартные метрические пространства, кроме C_p[a,b], являются банаховыми.)

Пример 1. Покажем полноту пространства C[a,b].

То, что это метрическое пространство, следует из того, что ρ = max|f-g| = max|(f-φ)+(φ-g)|≤max|f-g|+max|φ-g|. Пусть по метрике пространства C последовательность n(t)>→f(t), то есть ∃N=N(ε):∀n>N max|f_n(t)-f(t)| Комментарий. Тот факт, что в полных пространствах понятия замкнутости и полноты для подпространств совпадают, очень важен в приложениях. Однако, надо следить за полнотой исходного пространства.)

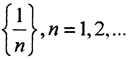
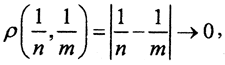
Примеры.1. Рассмотрим пространство (X,ρ), где X=(0,1), с метрикой ρ(x₁,x₂) = |x₁-x₂|. Последовательность фундаментальная, так как , при n,m →∞, но эта последовательность не сходится ни к одному элементу пространства (X,ρ), так как элемент, к которому она сходится, x = 0 не принадлежит пространству X.

3. Рассмотрим множество X=(0,1]. Оно, очевидно, не замкнуто и не полно. Пусть 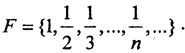. Это множество не замкнуто, хотя состоит из бесконечного числа замкнутых множеств, так как не любая последовательность из этого множества сходится к пределу, ему принадлежащему. Но оно не полно, так как предел этой последовательности равен нулю, которого нет в множестве X.

4. Покажем неполноту пространства C_p[a,b] при p = 1.

1. Сначала покажем, что это метрическое пространство. Ясно, что 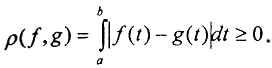. Покажем, что ρ(f,g)=0 ⇔ f=g.

2. Проверим третью аксиому:

Примеры.1. Верно ли, что последовательность 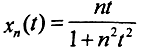n(t)>→0, если в C[0,1] и C₁[0,1]?

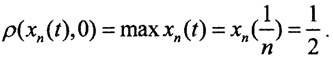
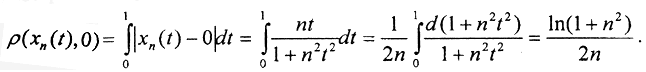
В пространстве C[0,1] . В пространстве C₁[0,1] . Тогда

2. Верно ли, что последовательность 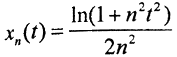n(t)>→0, если в пространстве C 1 [0,1]?

3. Показать полноту дискретного метрического пространства.

В дискретном метрическом пространстве все точки изолированные, поэтому фундаментальной последовательностью может быть только стационарная последовательность, которая всегда сходится.

4. Найти предел последовательности 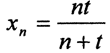в пространстве C[0,2], если он существует.

Необходимым условием сходимости последовательности в пространстве C[a,b] является существование предела x_n при каждом фиксированном t∈[a,b]. Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна.

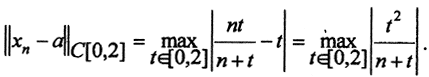
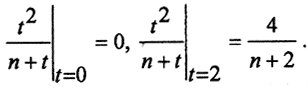
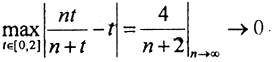
Проверим, сходится ли последовательность x_n к функции a(t) по норме пространства C[a,b], т.е. равномерно. Вычислим ||x_n-a||. По определению нормы: Вычислим максимум функции на отрезке [0,2]. Для этого вычислим критические точки: Таким образом, точками возможного экстремума являются точки t₁,t₂. Поскольку t₂ ∉[0,2], то остается лишь точка t₁. Вычислим также значение функции на концах отрезка: То есть Это означает, что последовательность x_n(t) в пространстве C[0,2] сходится к функции a(t)=t.

6. Сходится ли последовательность в пространстве l₃?

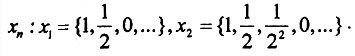
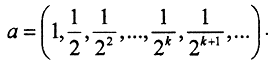
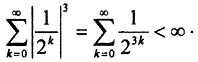
Необходимым условием сходимости последовательности в пространстве l_p, p≥1 является наличие покоординатного предела. Выпишем несколько членов последовательности: Ясно, что последовательность x_n покоординатно сходится к точке Заметим, что a∈l₃, так как Покажем, что последовательность x_n сходится к точке a по норме пространства l₃:

Следовательно,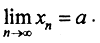

7. Сходится ли последовательность 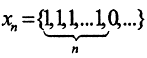в пространстве l₁?

Очевидно, что точка a = (1,1. 1. ) является покоординатным пределом последовательности, но a∉l₁, так как ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность x_n не имеет предела.

8. Показать, что пространство R n _p, p≥1, полное.

Пусть последовательность фундаментальна в R n _p. Тогда Отсюда следует покоординатная сходимость |x_in-x_im|_n,m→∞→0 и, следовательно, фундаментальность числовых последовательностей Но пространство действительных чисел полное и последовательности сходятся. Следовательно, сходится и последовательность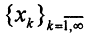

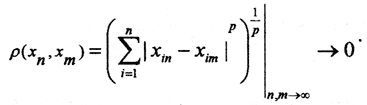
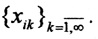
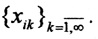
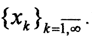
9. Дана последовательность

К какой последовательности она сходится покоординатно? Сходится ли она к тому же пределу в метриках пространств l₂, l₁, l?

Ясно, что покоординатно последовательность n> сходится к нулю. В соответствующих метриках она ведет себя так:

( Комментарий. Из предыдущего примера не следует, что всегда из покоординатной сходимости следует сходимость по метрике соответствующего пространства.)

10. Дана последовательность n>:x₁ = <1,1. 1. >, x₂ = <0,1. >. x_n = <0,0. 0,1. >Ясно, что покоординатно последовательность n> сходится к нулю. Однако в пространстве l: ρ(x_n,0)=sup<1,1. >=1≠0

11. Множество всех многочленов в пространстве C[a,b] не является замкнутым, так как, например, функцию можно приблизить частичными суммами ряда Тейлора, которые являются алгебраическими многочленами. Следовательно, множество всех многочленов в пространстве не содержит всех предельных точек, и, значит, оно не является замкнутым.

Источник