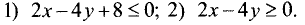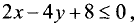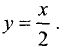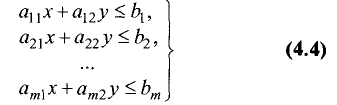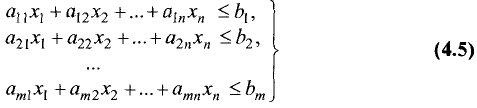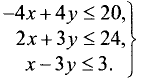Доказать что множество выпуклое
Выпуклые множества точек и их свойства с примерами решения и образцами выполнения
Основные определения:
Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.
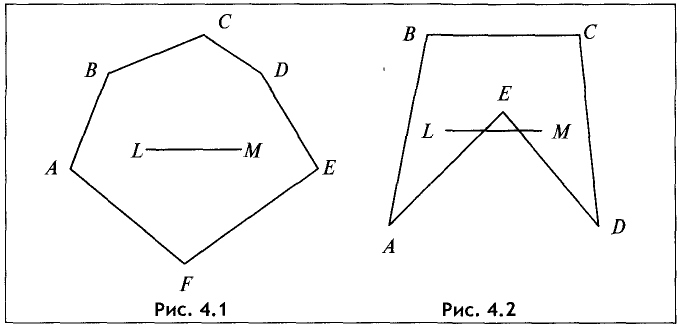
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.
Пересечение любого числа выпуклых множеств есть выпуклое
множество.
Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.
Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
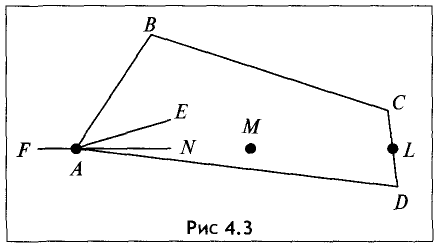
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.
Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.
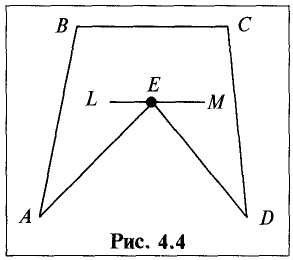
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).
Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.
Множество точек называется замкнутым, если оно включает все свои граничные точки.
Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.
Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.
Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.
Геометрический смысл решений неравенств
Рассмотрим решения неравенств с двумя переменными типа
Теорема:
Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой
включая и эту прямую, а другая полуплоскость — множеством решений неравенства
Пример:
Построить график множества решений следующих
неравенств:
Решение:
В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.
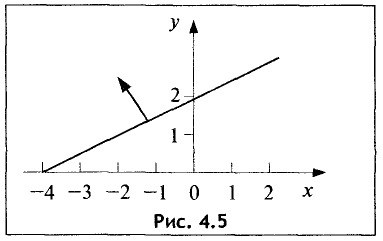
1.Границей первой полуплоскости является прямая
Представим уравнение этой прямой в виде 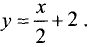
Ее график представлен на рис. 4.5.
Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство
видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.
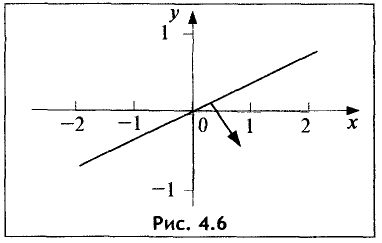
2.Границей второй полуплоскости является прямая
Представим это уравнение в виде
График исследуемой прямой представлен на рис. 4.6.
В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 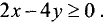
Основные свойства выпуклого множества точек
Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.
Теорема:
Множество решений совместной системы т линейных
неравенств с двумя переменными
является выпуклым многоугольником (или выпуклой многоугольной областью).
Знаки некоторых или всех неравенств могут быть
Эту теорему для n переменных можно сформулировать
следующим образом.
Теорема:
Множество решений совместной системы m линейных
неравенств с n переменными
является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.
Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.
Область решений системы, удовлетворяющая условиям неотрицательности 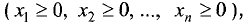
Пример:
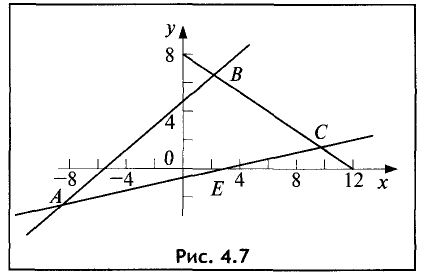
Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:
Решение:
Областью решений является треугольник ABC, представленный на рис. 4.7.
Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 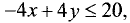
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Докажите, что множество F выпукло.
о/п. Предположим, что множество не является выпуклым.
Тогда
Далее,
Продолжая процесс, получим стягивающуюся последовательность, которая имеет предел Противоречие.
Не очень подробно, но идея ясна, думается.

Показать что множество D выпукло в том и только в том случае, когда при любых.
Докажите, что из всех треугольников, вписанных в данный круг, наибольшая площадь у равностороннего треугольника
Докажите, что из всех треугольников, вписанных в данный круг, наибольшая площадь у равностороннего.
Докажите, что множество перечислимо
Перечислимые множества.Множества A и B перечислимы. Докажите, что множество A ∩ B перечислимо.
Докажите, что универсальное множество неразрешимо
Докажите,что универсальное множество неразрешимо

Докажите, что множество M ⊂ N является перечислимым, если и только если оно является областью.
Докажите, что множество вычислимых функций неперечислимо
Докажите, что множество Fn вычислимых функций из N в N с областью определения N неперечислимо.
Определения выпуклого множества, выпуклой функции. Свойства выпуклых множеств. Свойство Лебега выпуклых функции.
Определение 1. Множество 

Определение 2. Множество 


Теорема 1. Пусть 


Теорема 2. Пусть 




Определение 3. Линейная комбинация 





Определение 4. Множество всевозможных выпуклых комбинаций любого конечного числа векторов из множества 
Очевидно, что для всякого множества 
Множество 
Пересечение всех выпуклых множеств, содержащих множество D, совпадает с convD.
Определение 5. Вектор x из выпуклого множества D называется крайней точкой множества D, если он не является выпуклой комбинацией никаких двух других векторов из D.
Легко увидеть, что любая крайняя точка выпуклого множества является его граничной точкой, но не всякая граничная точка является крайней.
Выпуклые функции.
Определение 1. Функция f, определенная на выпуклом множестве 







Определение 2. Функция f, определенная на выпуклом множестве 

Теорема 1. Для того, чтобы функция f, определенная на выпуклом множестве 



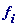


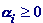

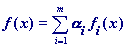
Пусть 








Теорема 3. Пусть 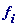



Пусть 









Теорема 4. Пусть функция 






Пусть 

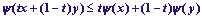







Пусть 


Что и требовалось доказать.
Далее установим связь между выпуклыми множествами и выпуклыми функциями. Пусть 

Теорема 7. Для того, чтобы функция f была выпуклой на выпуклом множестве 
Свойства выпуклых множеств
1. Пересечение любого числа выпуклых множеств является выпуклым множеством.
2. Объединение двух выпуклых множеств не обязательно выпукло.
Пример:объединение двух точек не есть выпуклое множество.
3. Геометрическая сумма 



также является выпуклым множеством.
4. Произведение выпуклого множества 
также является выпуклым множеством.
Эти утверждения следуют из определения выпуклого множества. Докажем,например, первое утверждение для пересечения двух множеств 



Из выпуклости A иBполучаем, что 
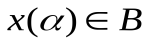


Определение.Крайней (экстремальной) точкойвыпуклого множества называется такая его точка, которая не может быть представлена в виде выпуклой комбинации двух различных точек этого множества.
В качестве примера приведем выпуклый многогранник. Его крайними точками являются его вершины.
Определение. МножествоS 
Примером строго выпуклого множества является замкнутый шар.
Множества Лебега
определяются и в этом случае так же, как для функций в евклидовом пространстве. [1]
Имеется в виду множество Лебега, построенное в 1905 г. ( Я. [2]
Теоремы об ограниченности множеств Лебега сильно выпуклой и выпуклой функций. [3]
Лебегу, если все ее множества Лебега, указанные в определении 1, при любом а измеримы. [5]
Множества В 1 измеримы как множества Лебега измеримых функций, а тогда и С тоже измеримы. [6]
Отсюда видно, что все множества Лебега первого типа функции f ( х) измеримы. [7]
В следующей теореме указывается одно важное свойство множеств Лебега сильно выпуклой функции. [8]
Функция /, определенная на выпуклом множестве X, называется квазивыпуклой, если все ее множества Лебега Хрвыпуклы. [10]
Если функция f ( х), заданная на множестве Е, такова, что ее множества Лебега какого-нибудь одного типа измеримы при всех а, то эта функция измерима. [11]
В то время как оценка Sn ( x) о ( пп) имеет место в каждой точке множества Лебега [ гл. II, (11.9) ] и, в частности, в каждой точке непрерывности /, оценка Sn ( х) о ( In n) 1 / в теореме (1.2) доказана лишь почти всюду, и неизвестно, какие свойства ( не тривиальные) функции гарантируют справедливость этой оценки в заданной точке. Недостаточность простой непрерывности следует из (1.2) гл. [12]
Дата добавления: 2019-07-15 ; просмотров: 503 ; Мы поможем в написании вашей работы!