Доказать что нулевой вектор единственный

Доказать что нулевой вектор единственный

Индивидуальные онлайн уроки: Отправьте запрос сейчас: irina@bodrenko.org
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Линейные пространства Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

Глава 2
ЛИНЕЙНЫЕ ПРОСТРАНСТВА

Из курса аналитической геометрии читатель знаком с операцией сложения свободных векторов и с операцией умножения вектора на вещественное число, а также со свойствами этих операций. В настоящей главе изучаются множества объектов любой природы, для элементов которых каким-либо способом (причем, безразлично каким) определены операция сложения элементов и операция умножения элемента на вещественное число, причем указанные операции обладают теми же свойствами, что и соответствующие операции над геометрическими векторами. Такие множества, называемые линейными пространствами, обладают целым рядом общих свойств, которые и будут установлены в настоящей главе.

§ 1. Понятие линейного пространства

1. Определение линейного пространства. Множество R элементов х, у, z. любой природы называется линейным (или аффинным) пространством, если выполнены следующие три требования.
I. Имеется правило, посредством которого любым двум элементам х и у множества R ставится в соответствие третий элемент z этого множества, называемый суммой элементов х и у и обозначаемый символом z = х + у.
П. Имеется правило, посредством которого любому элементу х множества R и любому вещественному числу λ ставится в соответствие элемент u этого множества, называемый произведением элемента х на число λ и обозначаемый символом u = λ х или

Легко убедиться в справедливости всех аксиом 1°-8°. В самом деле, справедливость аксиом 1° и 2° вытекает из переместаительного и сочетательного свойств произведения вещественных чисел; справедливость аксиом 3° и 4° вытекает из элементарных равенств

O₁ + O₂ = O₁, O₂ + O₁ =O₂, левые части которых (в силу аксиомы 1°) равны. Стало быть, в силу транзитивности знака «=» равны и правые части двух последних равенств, т.е. O₁ = O₂, и единственность нулевого элемента установлена.
Существование для каждого элемента х хотя бы одного противоположного элемента у утверждается в аксиоме 4°. Предположим, что для некоторого элемента х существует два противоположных элемента y₁ и y₂, так что х + y₁ =0 и х + y₂ = 0. Но тогда, в силу аксиом 3°, 2° и 1°, y₁ = y₁ + 0 = y₁+ (x + y₂) = (y₁ + x) + y₂ = 0 + y₂ = y₂ + О = y₂, т. е. y₁ = y₂, и единственность для каждого элемента х
противоположного элемента доказана. Теорема доказана.
Теорема 2.2. В произвольном линейном пространстве

Источник

22. Простейшие свойства векторного пространства

Рассмотрим те свойства векторного пространства, которые вытекают из его определения.

Свойство 1. В векторном пространстве V существует единственный нулевой вектор 0.

Доказательство. Допустим противное, что в V имеется два нулевых вектора 0 И Тогда по аксиомам 3° и 1° имеем

0 = 0 + = + 0 = .

Свойство 2. В векторном пространстве для любого вектора существует единственный противоположный вектор —.

Доказательство. См. доказательство теоремы 7 из §1.

Свойство 6. Для любых векторов , если A + B = А + С, то B = С.

Свойство 7. Для любых векторов Если A + B = А, то B = 0.

Доказательство. Следует из свойства 6.

Свойство 8. Для любого вектора Имеем 0×A = 0.

Доказательство. По аксиомам 8° и 6° имеем

Отсюда по свойству 7 0×A = 0.

Свойство 9. Для любого числа Имеем a×0 = 0.

Доказательство. По аксиоме 5° имеем

Отсюда по свойству 7 a×0 = 0.

Свойство 10. Пусть , . a×А = 0 Тогда и только тогда, когда a=0 Или А = 0.

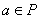
Противоречие. Свойство доказано.

Свойство 11. Пусть , . Тогда И

Доказательство. По аксиоме 6° и свойству 8 имеем

Отсюда в силу единственности противоположного вектора получаем требуемые равенства.

Свойство 12. Для любых , , Если

Доказательство. По определению разности, аксиоме 6 и свойству 11 имеем

Аналогичным образом доказываются следующие три свойства, которые рекомендуется доказать читателю самостоятельно.

Свойство 13. Для любых Имеем

Свойство 14. Для любых ,Если , То A = B.

Свойство 15. Для любых , Если , То

Источник

LINALG (Теория по линейной алгебре (определения, доказательства, формулы))

Описание файла

Файл «LINALG» внутри архива находится в следующих папках: Теория по линейной алгебре (определения, доказательства, формулы), V782RhwLleN, Linal. Документ из архива «Теория по линейной алгебре (определения, доказательства, формулы)», который расположен в категории «разное». Всё это находится в предмете «линейная алгебра и фнп» из второго семестра, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана. Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «остальное», в предмете «линейная алгебра и фнп» в общих файлах.

Онлайн просмотр документа «LINALG»

Текст из документа «LINALG»

Глава 1. Элементы линейной алгебры

1.1. Понятие линейного пространства

В курсе аналитической геометрии и векторной алгебры мы изучали понятия арифметического и геометрического вектора и поняли, что по своим алгебраическим свойствам, если ограничиться операциями сложения и умножения на число, эти объекты совершенно одинаковы. Это побуждает нас обобщить понятие вектора, рассматривая его исключительно в плане свойств линейных операций (т.е. сложения и умножения на число), с тем, чтобы частные виды векторов (например, геометрические или арифметические векторы) можно было изучать в рамках единой теории. Отчасти мы уже это и делали, рассматривая понятия базиса на множествах геометрических или арифметических векторов.

Обобщение понятия вектора достигается через определение линейного пространства.

Договоримся впредь знак умножения вектора на число опускать.

Можно было бы определить точно так же умножение вектора на комплексное число. Мы в нашем курсе ограничимся по существу только умножением на вещественные числа и, желая подчеркнуть это, будем называть только что определенное линейное пространство вещественным линейным пространством.

3) Рассмотрим на первый взгляд несколько необычный пример линейного пространства.

Для двух произвольных функций определим их сумму как функцию так, что

(обычное «поточечное» сложение функций, известное из школьной алгебры в виде процедуры сложения «графиков», причем, как известно из курса математического анализа, сумма непрерывных функций непрерывна).

Для любой функции и произвольного вещественного введем новую функцию (результат умножения на ) так, что

(также известная из школы процедура «растяжения» графика в заданное число раз, преобразующая непрерывную функцию в непрерывную).

Таким образом, на непрерывную функцию можно смотреть как на вектор, то есть, как на элемент соответствующего векторного пространства.

Рассмотрим теперь некоторые следствия из определения линейного пространства.

Единственность нулевого вектора

Докажем, что нулевой вектор линейного пространства определен однозначно.

Предположим, что существуют два нулевых вектора: и ; имеем:

Единственность противоположного вектора

Докажем, что для каждого вектора существует единственный противоположный к нему вектор.

Пусть для некоторого вектора нашлись два противоположных к нему вектора: и ; тогда получим:

(заметим, что в этом выводе использованы свойства (1)-(4) из определения линейного пространства).

Мы можем также ввести операцию вычитания для векторов, положив для любых двух векторов и

В силу единственности противоположного вектора можно утверждать, что в линейном пространстве любое уравнение вида

Результат умножения на нуль

Докажем, что для любого вектора (т.е., число 0, будучи умножено на любой вектор, дает нулевой вектор).

Результат умножения на

Результат умножения произвольного числа на нулевой вектор

В самом деле, для произвольного вектора : 0 1 = (0a)=

Заметим, что все пять следствий из аксиом линейного пространства, т.е. из свойств (1)-(8), доказаны чисто алгебраически. Для геометрических и арифметических векторов они совершенно очевидны.

1.2. Линейно зависимые и линейно независимые системы векторов. Базис и размерность.

Определения линейной комбинации векторов, линейно зависимых, линейно независимых систем векторов, равно как и понятия базиса и размерности, которые были даны в первом семестре применительно к геометрическим и арифметическим векторам, без всяких изменений переносятся на случай произвольного линейного пространства. Здесь эти определения и доказанные на их основе теоремы заново формулироваться не будут. Напомним, что под системой векторов понимается, как и раньше, произвольная (состоящая не менее, чем из одного вектора) конечная последовательность векторов.

Здесь же мы рассмотрим интересный пример линейного пространства без базиса, т.е. такого линейного пространства, в котором любая линейно независимая система может быть расширена без утраты свойства линейной независимости.

Определение 1.2 Линейное пространство, обладающее базисом, называется конечномерным.

Линейное пространство без базиса называется бесконечномерным.

В рамках нашего курса мы будем рассматривать только конечномерные пространства.

1.3. Подпространства и линейные оболочки

Утверждение 1.1 Подмножество линейного пространства является подпространством тогда и только тогда, когда для любой системы векторов в оно содержит их произвольную линейную комбинацию.

Примеры. 1) В пространстве всех геометрических векторов подмножество всех векторов, параллельных некоторой плоскости, будет подпространством, а подмножество всех векторов, концы которых лежат на некоторой плоскости, не будет подпространством.

2) Множество всех решений однородной линейной системы есть, как мы видели в первом семестре, векторное пространство, которое будет ни чем иным, как подпространством арифметического пространства (где в данном случае есть число неизвестных системы).

Источник

Глава 1 Элементы линейной алгебры 1 1 Понятие линейного пространства

Глава 1. Элементы линейной алгебры

1.1. Понятие линейного пространства

В курсе аналитической геометрии и векторной алгебры мы изучали понятия арифметического и геометрического вектора и поняли, что по своим алгебраическим свойствам, если ограничиться операциями сложения и умножения на число, эти объекты совершенно одинаковы. Это побуждает нас обобщить понятие вектора, рассматривая его исключительно в плане свойств линейных операций (т.е. сложения и умножения на число), с тем, чтобы частные виды векторов (например, геометрические или арифметические векторы) можно было изучать в рамках единой теории. Отчасти мы уже это и делали, рассматривая понятия базиса на множествах геометрических или арифметических векторов.

Обобщение понятия вектора достигается через определение линейного пространства.

Договоримся впредь знак умножения вектора на число опускать.

3) Рассмотрим на первый взгляд несколько необычный пример линейного пространства.

Для двух произвольных функций определим их сумму как функцию так, что

(обычное «поточечное» сложение функций, известное из школьной алгебры в виде процедуры сложения «графиков», причем, как известно из курса математического анализа, сумма непрерывных функций непрерывна).

Для любой функции и произвольного вещественного введем новую функцию (результат умножения на ) так, что

(также известная из школы процедура «растяжения» графика в заданное число раз, преобразующая непрерывную функцию в непрерывную).

Таким образом, на непрерывную функцию можно смотреть как на вектор, то есть, как на элемент соответствующего векторного пространства.

Рассмотрим теперь некоторые следствия из определения линейного пространства.

Единственность нулевого вектора

Докажем, что нулевой вектор линейного пространства определен однозначно.

Предположим, что существуют два нулевых вектора: и ; имеем:

Единственность противоположного вектора

Докажем, что для каждого вектора существует единственный противоположный к нему вектор.

Пусть для некоторого вектора нашлись два противоположных к нему вектора: и ; тогда получим:

(заметим, что в этом выводе использованы свойства (1)-(4) из определения линейного пространства).

Мы можем также ввести операцию вычитания для векторов, положив для любых двух векторов и

В силу единственности противоположного вектора можно утверждать, что в линейном пространстве любое уравнение вида

Результат умножения на нуль

Докажем, что для любого вектора (т.е., число 0, будучи умножено на любой вектор, дает нулевой вектор).

, откуда, (использованы свойства (6) и (8) из определения линейного пространства, а также предыдущее следствие).

Результат умножения на

, откуда в силу единственности противоположного вектора получаем доказываемое.

Результат умножения произвольного числа на нулевой вектор

В самом деле, для произвольного вектора

Заметим, что все пять следствий из аксиом линейного пространства, т.е. из свойств (1)-(8), доказаны чисто алгебраически. Для геометрических и арифметических векторов они совершенно очевидны.

1.2. Линейно зависимые и линейно независимые системы векторов. Базис и размерность.

Определения линейной комбинации векторов, линейно зависимых, линейно независимых систем векторов, равно как и понятия базиса и размерности, которые были даны в первом семестре применительно к геометрическим и арифметическим векторам, без всяких изменений переносятся на случай произвольного линейного пространства. Здесь эти определения и доказанные на их основе теоремы заново формулироваться не будут. Напомним, что под системой векторов понимается, как и раньше, произвольная (состоящая не менее, чем из одного вектора) конечная последовательность векторов.

В рамках нашего курса мы будем рассматривать только конечномерные пространства.

1.3. Подпространства и линейные оболочки

Утверждение 1.1 Подмножество линейного пространства является подпространством тогда и только тогда, когда для любой системы векторов в оно содержит их произвольную линейную комбинацию.

2) Множество всех решений однородной линейной системы есть, как мы видели в первом семестре, векторное пространство, которое будет ни чем иным, как подпространством арифметического пространства (где в данном случае есть число неизвестных системы).

Определение 1.4 Линейной оболочкой системы векторов некоторого линейного пространства называется множество всех линейных комбинаций векторов системы.

В первом семестре мы определили понятие ранга системы векторов как наибольшего числа линейно независимых векторов системы. Нетрудно доказать следующий результат:

Утверждение 1.2 Ранг системы векторов равен размерности ее линейной оболочки.

Рис. 1.1

1.4. Преобразования базисов

Возникает задача: связать между собой координаты произвольного вектора в двух различных базисах. Эту задачу будем называть задачей преобразования базисов.

Легко доказать (по аналогии с доказательством ассоциативности умножения числовых матриц) следующее равенство:

С использованием векторных матриц-строк удобно записывать разложение произвольных систем векторов по данному базису.

Или, с использованием векторных матриц-строк:

Утверждение 1.3 Если система линейно независима, то столбцы матрицы линейно независимы.

С учетом этих равенств рассмотрим линейную комбинацию

Итак, мы получили нетривиальную линейную комбинацию линейно независимых векторов, равную нулю, что невозможно.

Можно заметить, что, проводя рассуждения доказательства утверждения 1.3 в обратном порядке, получим, что верно и обратное: если столбцы матрицы линейно независимы, то система векторов линейно независима. Следовательно, для распознавания линейной независимости произвольной системы векторов конечномерного линейного пространства достаточно составить матрицу из столбцов координат векторов системы в произвольном фиксированном базисе и доказать линейную независимость этих столбцов, используя, например, метод элементарных преобразований (т.е., вычислив ранг составленной матрицы).

Для одного вектора его разложение по базису задается в виде:

Вернемся к задаче преобразования базисов. Запишем разложение нового («штрихованного») базиса в старом (не «штрихованном»):

Тогда для разложения вектора в новом базисе получим:

Отсюда по теореме о единственности разложения вектора по базису (первый семестр!)

Так как матрица не вырождена, то

Итак, чтобы вычислить столбец координат вектора в новом базисе, достаточно матрицу, обратную к матрице перехода, умножить на столбец координат вектора в старом базисе.

Таким образом, можно заметить, что сами базисы и координаты векторов в базисах при переходе от базиса к базису перевычисляются «зеркально» по отношению к друг другу.

Составляем матрицы перехода от к и от к (по столбцам координат векторов базисов и ). Пусть это будут матрицы и соответственно. Тогда используя утверждение 1.4, легко получим (см. рис. 1.2):

Источник