Доказать что осевая симметрия является движением

Понятие движения

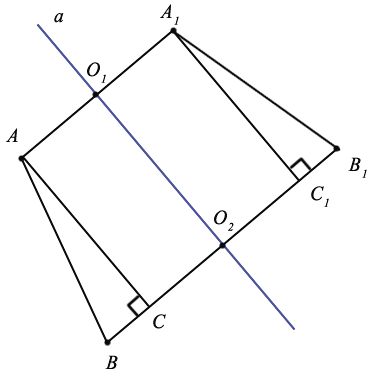
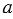
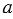
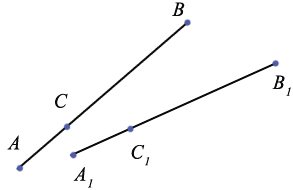
Пусть прямая — ось симметрии. Возьмем две произвольные точки А и В, которые лежат по одну сторону от оси симметрии, и симметричные относительно прямой им точки А₁ и В₁:

Из точек А и А₁ проведем перпендикуляры АС и А₁С₁ к прямой ВВ₁. Рассмотрим АВС и А₁В₁С₁: Они являются прямоугольными. Нам известно, что две прямые перпендикулярные к третьей прямой не пересекаются (т.е. являются параллельными). Значит, из того что АА₁ и ВВ₁, следует, что то АА₁ВВ₁, аналогично, АСА₁С₁. Т.е. мы получили, что в четырехугольнике АСС₁А₁ стороны попарно параллельны, значит, этот четырехугольник является параллелограммом, а, следовательно, АС=А₁С₁. Так как АА₁ВВ₁, то АО₁=СО₂=О₂С₁=О₁А₁ (данное равенство верно, так как вершины прямоугольника симметричны относительно серединного перпендикуляра, который проведен к его сторонам), поэтому ВС=ВО₂—СО₂=О₂В₁—О₂С₁=С₁В₁. Итак, мы получили, что в рассматриваемых треугольниках АС=А₁С₁ и ВС=С₁В₁, значит, АВС=А₁В₁С₁ (по двум катетам). Следовательно, АВ=А₁В₁, то есть расстояние между точками А и В равно расстоянию между симметричными им точками А₁ и В₁.

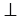
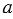
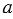
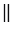
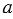
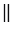
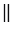
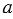
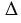
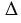
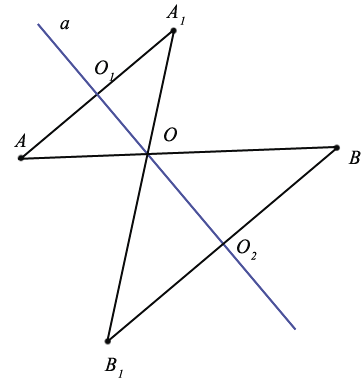
Рассмотрим случай, когда точки А и В лежат по разные стороны от оси симметрии:

При других расположениях точек А, В и А₁, В₁ также получается, что АВ=А₁В₁:

Итак, мы получили, что осевая симметрия является отображением, которое сохраняет расстояния между точками.

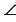
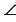
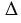
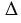
Так как точка А симметрична точке А₁ и В симметрична точке В₁, то А₁О=ОА и В₁О=ОВ. АОВ=В₁ОА₁, так как они вертикальные. Следовательно, АОВ=В₁ОА₁ (по I признаку равенства треугольников) и АВ=А₁В₁, то есть расстояние между точками А и В равно расстоянию между симметричными им точками А₁ и В₁. Значит, центральная симметрия является отображением, которое сохраняет расстояния между точками.

Любое отображение, которое сохраняет расстояния между точками называется движением (или перемещением).

Поясним на примере осевой симметрии, по какой причине отображение, которое сохраняет расстояния, называют движением:

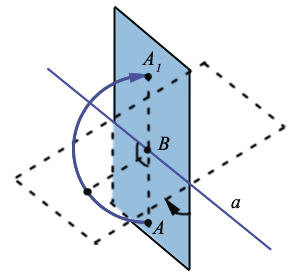
На рисунке видно, что осевую симметрию можно представить как поворот плоскости в пространстве на 180 0 вокруг оси .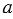

Теорема

Доказательство

Дано: движение, отрезок АВ, А отображается в А₁, В отображается в В₁

Доказать, что отрезок АВ отображается на отрезок А₁В₁

Доказательство:

Возьмем произвольную точку С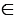АВ, которая отображается в точку С₁.

АВ=АС+СВ.

При движении расстояния сохраняются, поэтому АВ=А₁В₁, АС=А₁С₁ и СВ=С₁В₁. (1)

Из данных равенств имеем, что А₁В₁=АВ=АС+СВ=А₁С₁+С₁В₁, следовательно, С₁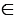А₁В₁ (если предположить обратное, то будет выполнятся неравенство А₁С₁+С₁В₁>A₁B₁). Значит, точки отрезка АВ отображаются в точки отрезка А₁В₁.

Возьмем произвольную точку С₁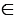А₁В₁, при этом при заданном движении точка С отображается в данную точку С₁. Из соотношений (1) и равенства А₁В₁=А₁С₁+С₁В₁, следует, что АС+СВ=АВ, а, значит, САВ. Т.е. в каждую точку С₁ отрезка А₁В₁ отображается какая-нибудь точка С отрезка АВ. Теорема доказана.

Следствие

Поделись с друзьями в социальных сетях:

Источник

Что такое движения плоскости: центральная и осевая симметрия

Если каждой точке из плоскости можно поставить в соответствие точку из этой же плоскости, причем этим сопоставлением все точки плоскости исчерпываются, то перед нами отображение плоскости на себя. Любое отображение плоскости на себя, сохраняющее расстояния между точками, есть движение плоскости.

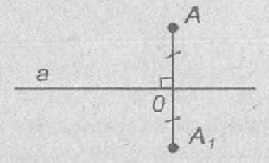
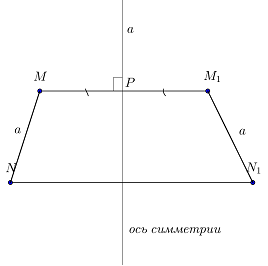
Точки А и А₁ являются симметричными относительно прямой а, если она проходит через центр отрезка АА1, и если она расположена под прямым углом к этому отрезку. Все точки рассматриваемой прямой а считается симметричными сами себе.

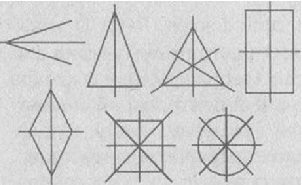
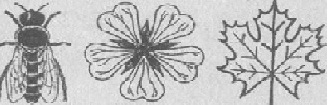
Фигура считается симметричной относительно прямой а, если для каждой точки рассматриваемой фигуры симметричная для нее точка относительно прямой а также находится на этой фигуре. Прямая а является в этом случае осью симметрии фигуры (фигура с осевой симметрией). Фигуры, с осевой симметрией, приведены на рисунке.

Для неразвернутого угла существует единственная ось симметрии — это биссектриса данного угла. Для равнобедренного треугольника есть единственная ось симметрии, для равностороннего треугольника — три оси. Для прямоугольника и ромба существует две оси симметрии, а для квадрата — целых четыре. Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры. Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.

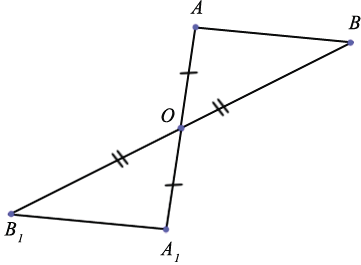
Две точки А и A₁ симметричны относительно точки О, если она является центром отрезка АА1 (смотри первый рисунок). Точка О является симметричной самой себе.

Фигура симметрична относительно точки О, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Точка О это центр симметрии (фигура с центральной симметрией). Есть фигуры с центральной симметрией это, например, окружность и параллелограмм. У окружности центр симметрии — это ее центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали.

Множество окружающих нас предметов имеют центр или ось симметрии. С симметрией приходится часто встречаться в искусстве, архитектуре, технике.

Поскольку осевая симметрия представляет отображение плоскости на себя, которое сохраняет расстояния между точками, она является движением плоскости (поворот плоскости в пространстве на развернутый угол вокруг прямой а).

Центральная симметрия плоскости есть движение.

Теорема: при движении точки, которые лежат на прямой, отображаются в точки, которые находятся на прямой, при этом сохраняется последовательность их расположения друг относительно друга. Это означает, что если точки А, В, С одной прямой, отображаются в некоторые точки А₁, В₁, С₁ то эти данные также будут лежать на прямой; если точка В находится между точками А и С, то точка В₁ также находится между точками А₁ и С₁.

Во время движения прямая, превращается в прямую, отрезок, треугольник отображается в равный для него треугольник, отображается на отрезок, луч отображается на луч, угол отображается на такой же угол.

Всякое движение переводит параллельные прямые в параллельные, а перпендикулярные прямые — в перпендикулярные.

Два движения, выполненные последовательно, снова дают движение.

Источник

Урок «Движения. Осевая симметрия»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Мы продолжаем знакомство с движением.

На прошлом занятии вы познакомились с одним из видов движения — центральной симметрией.

Вспомним, что центральная симметрия — это такое отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1, относительно центра симметрии точки В.

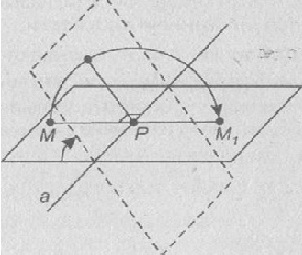
Отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1 относительно оси а называется осевой симметрией с осью а.

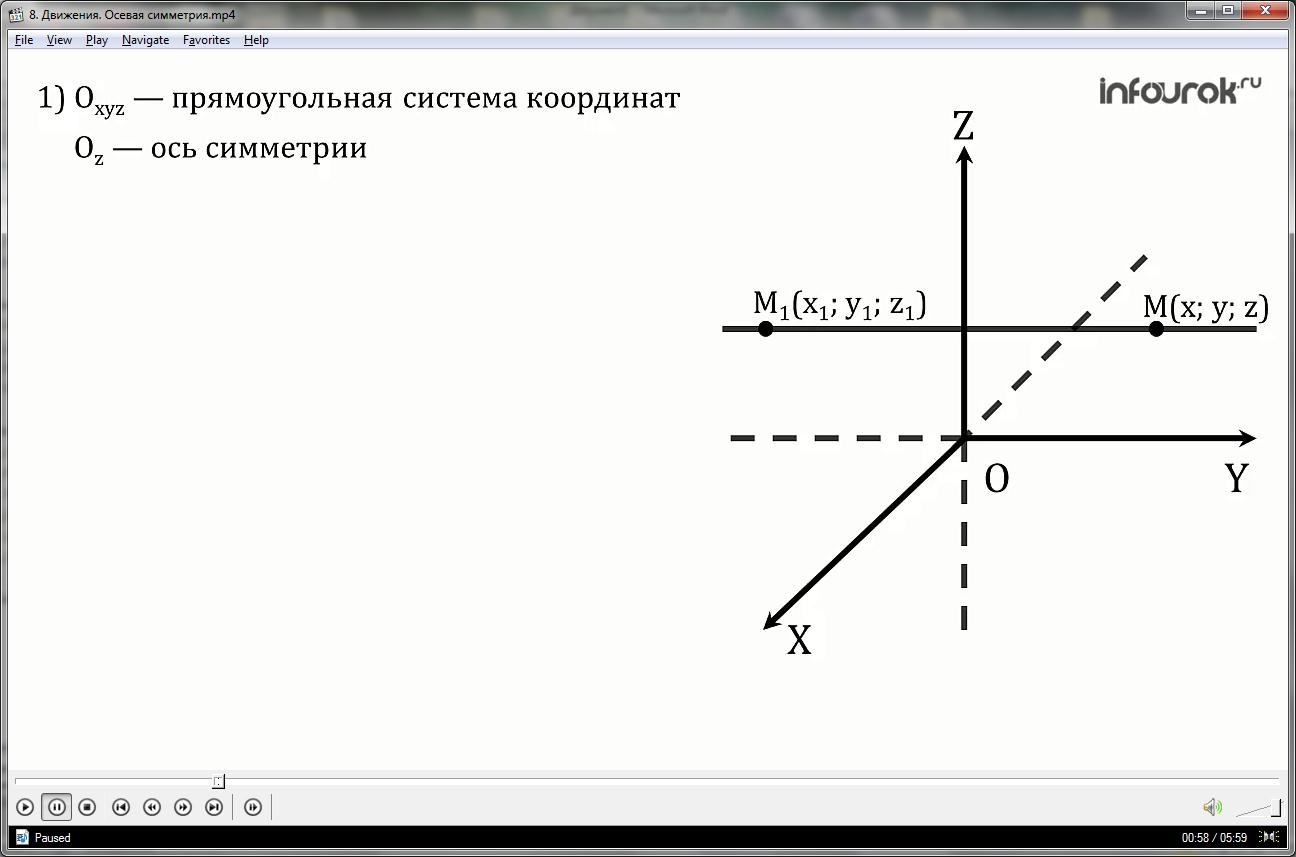
1. Введём декартову (прямоугольную) систему координат Оxyz так, чтобы ось Оz совпала с осью симметрии.

а) проходит через середину отрезка МM1;

б) перпендикулярна отрезку ММ1.

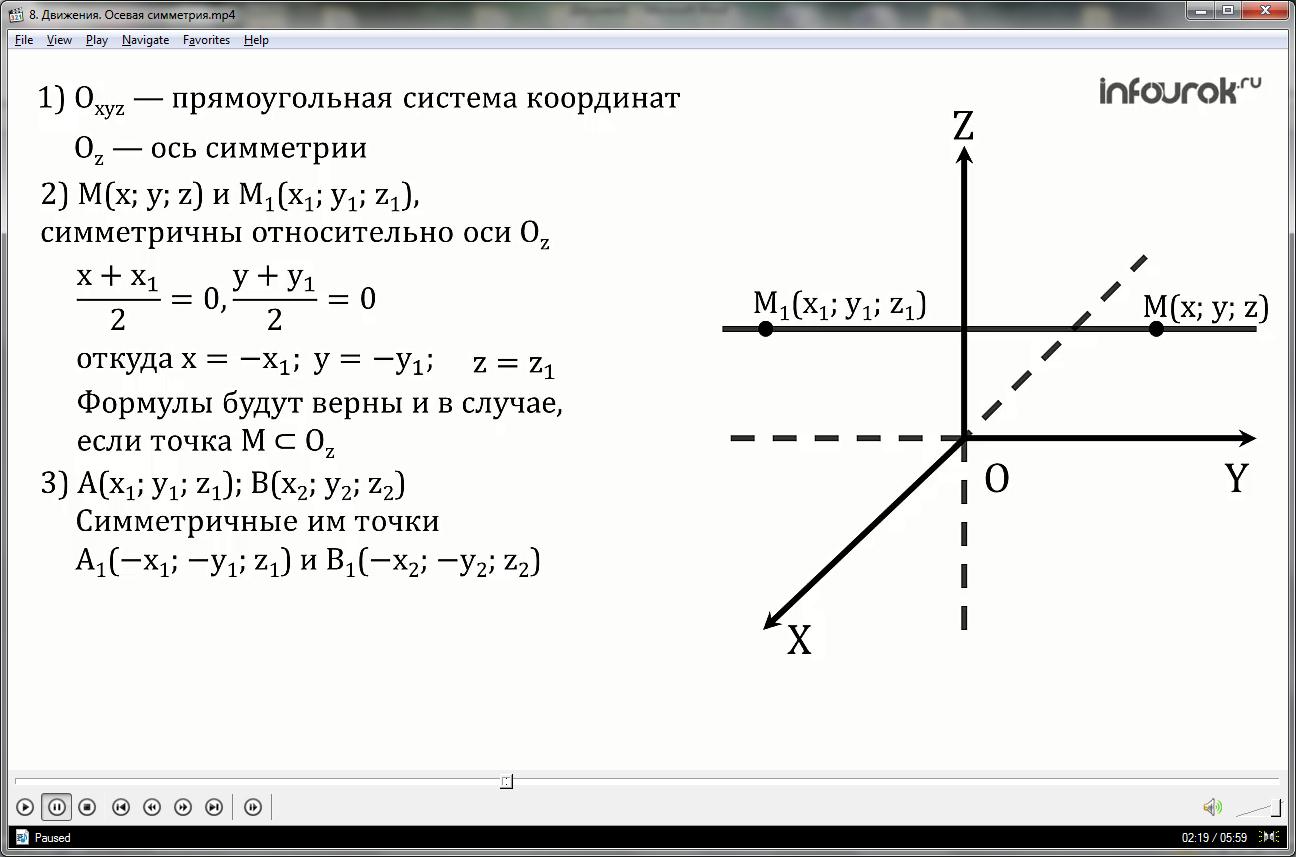
Из первого условия по формулам для координат середины отрезка имеем:

Из второго условия можно сделать вывод, о том, что z=z1.

Данные формулы будут верны и в случае, если точка М принадлежит оси Оz.

3. Рассмотрим любые две точки: А — с координатами (x1;y1;z1) и В — с координатами (x2;y2;z2) и докажем, что расстояние между точками А1 и В1, которые им симметричны, равно АВ.

Точки А1 и В1 имеют координаты

А1 (-x1;-y1;z1) и В1 (-x2;-y2;z2).

По формуле расстояний между двумя точками, найдём:

Очевидно, что длина отрезка АВ равна длине отрезка A1B1, то есть расстояние между точками сохранено.

Таким образом, мы доказали, что осевая симметрия является движением.

Рассмотрим решение задач, применяя полученные знания.

1. Так как ось симметрии а и прямая l не параллельны, то а пересекается с l в некоторой точке А.

Выберем любую точку N на прямой l.

Построим отрезок NE перпендикулярно к оси симметрии а.

Затем продолжим отрезок NE за точку Е на расстояние EF=NE.

Соединим точки F и А.

2. Рассмотрим прямоугольные треугольники AEF и AEN.

EF=NE (по построению), АЕ — общий катет.

Таким образом, прямоугольные треугольники AEF и AEN равны.

Известно, ABCDA1B1C1D1 — куб, длина ребра АВ равна а. Точка D отображается в точку D2 при осевой симметрии относительно прямой В1 D1. Найти ВD2.

1.Отрезок DD1 перпендикулярен плоскости A1C1D1 верхнего основания куба.

По определению осевой симметрии отрезки DD1 и D1D2 равны. Значит DD2=2а

2.Из прямоугольного треугольника ABD найдём гипотенузу BD по теореме Пифагора:

3.Так как треугольник BDD2 так же прямоугольный, то по теореме Пифагора найдем длину искомого отрезка ВD2:

Таким образом, длина отрезка ВD2 равна а√6.

Источник

Что называется осевой симметрией

Что такое осевая симметрия в геометрии

Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.

Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – S_n, таким образом симметрия точек A и B обозначается так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.

Свойства осевой симметрии

Теорема и доказательство

Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.

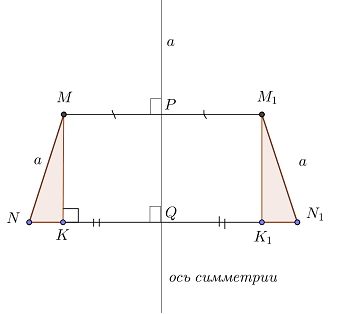
Если отрезок MN симметричен отрезку M₁N₁ относительно прямой a, то MN = M₁N₁.

Чтобы доказать, что MN = M₁N₁, сделаем дополнительные построения:

Докажем, что прямоугольные треугольники MNK и M₁N₁K₁ равны. Стороны MN и M₁N₁ являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

Точка N отобразилась в точку N₁, значит:

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M₁N₁, что и требовалось доказать.

Фигуры, обладающие симметрией

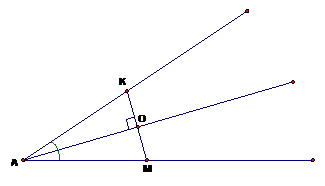
Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

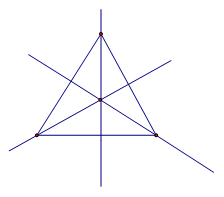
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

Источник

Презентация по геометрии на тему «Движения и симметрия» 11 класс

Описание презентации по отдельным слайдам:

Движение в пространстве 11 класс

Понятие движения Движение – это отображение пространства на себя, сохраняющее расстояния между точками

Виды движения Центральная симметрия Осевая симметрия Зеркальная симметрия Параллельный перенос

Центральная симметрия Центральная симметрия — отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.

Осевая симметрия Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а.

Осевая симметрия вокруг нас

Зеркальная симметрия Зеркальной симметрией (относительно плоскости ) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости  точку М1.

Зеркальная симметрия является движением. Для этого введем прямоугольную систему координат Oxyz так, чтобы плоскость Оху совпала с плоскостью симметрии, и установим связь между координатами двух точек М(х; у;z) и М1(х1; у1; z1), симметричных относительно плоскости Оху. Если точка М не лежит в плоскости Оху, то эта плоскость: 1) проходит через середину отрезка ММ1 ; 2) перпендикулярна к нему. М К К  МК=М1К1 М1 К1

Фигуры, симметричные относительно плоскости Фигура ( тело) называется симметричной относительно некоторой плоскости, если эта плоскость разбивает фигуру на две равные симметричные части. Сколько плоскостей симметрии имеет куб? Ответы : 2; 4; 5; 6; 9

Симметрия в пирамиде Верно ли высказывание: правильная четырехугольная пирамида имеет четыре плоскости симметрии

Задачи 1. Сколько плоскостей симметрии имеет пирамида, в основании которой лежит прямоугольник, ромб? Какое дополнительное условие должно присутствовать в условии задачи, чтобы ваш ответ был верен?

Зеркальная симметрия в призме 1)Сколько плоскостей симметрии имеет правильная четырехугольная призма? Ответы: а)2 б)4 в)3 г)5 д)12 2)Сколько плоскостей симметрии имеет прямая призма, в основании которой лежит прямоугольник? Ответы: а)2 б)3 в)1 г)4 д)8 3)Сколько плоскостей симметрии имеет правильная треугольная призма? Ответы: а)4 б)3 в)1 г)2 д)5 г) 5 б) 3 а) 4

Зеркальная симметрия в архитектуре г. Санкт- Петербурга Александринский театр Исаакиевский собор Сколько плоскостей симметрии имеют данные объекты?

Улица России имеет плоскость симметрии в общем обзоре, но не все детали в архитектуре зданий симметричны.

Пример зеркальной симметрии Центральный зал станции

Зеркально симметричные объекты Осевая симметрия Зеркальная симметрия Центральная симметрия

Параллельный перенос Параллельным переносом на вектор р называется отображение пространства на себя, при котором любая точка М переходит в такую точку М1, что ММ1 =р М М1 М

A B C D A’ B’ C’ D’ Параллельный перенос

Параллельный перенос является движением. При параллельном переносе на вектор р любые две точки А и В переходят в точки А1и В1 такие, что АА1 = р и BB1= р. Требуется доказать, что А1В1=АВ. По правилу треугольника АВ1 = =АА1+А1 В1 C другой стороны, АВ1=АВ+ВВ1 (рис. 134, б). Из этих двух равенств получаем АА1+А1В1 = AВ + p, или р+А1В1 =АВ+p, откуда А1B1 =АВ. Следовательно, А1В1=АВ, что и требовалось доказать. B1 В

Параллельный перенос Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину. B1 В

Параллельный перенос различных фигур

Параллельный перенос А В

Кувшин. Плоская симметричная фигура. Крапива. Винтовая симметрия. Звезда. Симметрия восьмого порядка.

Зеркальная симметрия в природе

Зеркальная симметрия в природе

Симметрия переноса. Симметрия. Орнамент.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-490161

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил разработать концепцию развития допобразования детей до 2030 года

Время чтения: 2 минуты

Создана Ассоциация руководителей школ России и Беларуси

Время чтения: 1 минута

В России планируют создавать пространства для подростков

Время чтения: 2 минуты

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

Учителя Кубани смогут получить миллион рублей на взнос по ипотеке

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник