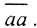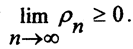Доказать что пространство полное

∑ i = 1 n ( x i ( k ) − x i ( m ) ) 2 ϵ <\displaystyle <\sqrt <\sum _^\left(x_^<(k)>-x_^<(m)>\right)^<2>>> .

| x n ( t ) − x m ( t ) | ϵ <\displaystyle |x_(t)-x_(t)| ,

это означает, что последовательность < x n ( t ) ><\displaystyle \(t)\>> сходится равномерно, а так как предел равномерно сходящейся последовательности непрерывных функций есть непрерывная функция

x ( t ) = lim n → ∞ x n ( t ) <\displaystyle x(t)=\lim _x_(t)>

Если в неравенстве

| x n ( t ) − x m ( t ) | ϵ <\displaystyle |x_(t)-x_(t)| ,

Пример 6. Покажем что пространство непрерывных функций C 2 [ − 1 ; 1 ] <\displaystyle C_<2>[-1;1]> не является полным. Рассмотрим последовательность непрерывных функций вида

Последовательность < g n ><\displaystyle \\>> является фундаментальной. Действительно, рассмотрим две функции g n <\displaystyle g_> и g m <\displaystyle g_> , они отличаются друг от друга лишь на отрезке ширины

причём абсолютная величина различия не превышает 1, следовательно

Однако последовательность < g n ><\displaystyle \\>> не сходится ни к одной непрерывной функции из C 2 [ 0 ; 1 ] <\displaystyle C_<2>[0;1]> . Для доказательства этого факта рассмотрим произвольную функцию f ∈ C 2 [ − 1 ; 1 ] <\displaystyle f\in C_<2>[-1;1]> и разрывную функцию

В силу интегрального неравенства Минковского (это неравенство справедливо и для кусочно-непрерывных функций):

∫ − 1 1 [ f ( t ) − g ( t ) ] 2 d t ≤ ∫ − 1 1 [ f ( t ) − g n ( t ) ] 2 d t + ∫ − 1 1 [ g n ( t ) − g ( t ) ] 2 d t <\displaystyle <\sqrt <\int \limits _<-1>^<1>[f(t)-g(t)]^<2>dt>>\leq <\sqrt <\int \limits _<-1>^<1>[f(t)-g_(t)]^<2>dt>>+<\sqrt <\int \limits _<-1>^<1>[g_(t)-g(t)]^<2>dt>>> .

∫ − 1 1 [ g n ( t ) − g ( t ) ] 2 d t ≤ 2 n <\displaystyle \int \limits _<-1>^<1>[g_(t)-g(t)]^<2>dt\leq <\frac <2>>>

lim n → ∞ ∫ − 1 1 [ g n ( t ) − g ( t ) ] 2 d t = 0 <\displaystyle \lim _\int \limits _<-1>^<1>[g_(t)-g(t)]^<2>dt=0> .

Теоремы о полных пространствах [ править ]

Теорема 2 (о вложенных шарах). Для того, чтобы метрическое пространство было полным необходимо и достаточно, чтобы в нём всякая последовательность вложенных друг в друга замкнутых шаров, радиусы которых стремятся к нулю, имела непустое пересечение.

Последовательность центров x n <\displaystyle x_> является фундаментальной, так как

По определению пересечения множеств

Следующий номер n_<1>>»> n 2 > n 1 <\displaystyle n_<2>>n_<1>> n_<1>>»/> выберем таким образом, чтобы при n_<2>>»> n > n 2 <\displaystyle n>n_<2>> n_<2>>»/> выполнялось неравенство

Пусть мы уже выбрали номера

Номер n_>»> n k + 1 > n k <\displaystyle n_>n_> n_>»/> выберем так, чтобы при n_>»> n > n k + 1 <\displaystyle n>n_> n_>»/> выполнялось неравенство

Доказательство проведём от противного.

и так далее. Таким образом можно получить последовательность вложенных друг в друга замкнутых шаров

радиусы которых стремятся к нулю, причём

По теореме о вложенных шарах пересечение

что противоречит исходному предположению. Теорема доказана.

Пополнение метрического пространства [ править ]

Полнота пространства является очень важным с точки зрения анализа свойством, так как в неполных пространствах не все фундаментальные последовательности имеют предел. Возникает вопрос: можно ли расширить неполное пространство таким образом, чтобы оно стало полным. Оказывается, что это всегда можно сделать, причём такое расширение является, по-существу, единственным.

Напомним, что множество

называется всюду плотным в M, если имеет место равенство

Справедлива следующая теорема:

Обозначать факт эквивалентности двух последовательностей будем следующим образом:

\\>\sim \\>> .

Используя аксиомы метрики, можно показать, что введённое нами отношение эквивалентности двух последовательностей является рефлексивным, симметричным и транзитивным.

\\>\in \eta _<2>>

В силу неравенства четырёхугольника:

По неравенству четырёхугольника

\\>\sim \\>> ,

то по введённому определению эквивалентности

Таким образом, значение предела действительно не зависит от выбора последовательности.

Для доказательства аксиомы треугольника рассмотрим три класса эквивалентности

\eta _<3>\in R’> .

Выберем в каждом из этих классов по одной последовательности

Переходя в этом неравенстве к пределу, получим

y=\lim _y_> ,

Тогда при n_<0>>»> n > n 0 <\displaystyle n>n_<0>> n_<0>>»/> будем иметь

\lim _y_=y’> ,

а в пространстве R 2 <\displaystyle R_<2>>

\lim _y_=y»> ,

то в силу непрерывности метрики

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Определить полноту пространства

Здравствуйте. Ребят, очень нужна помощь.

Задача звучит следующим образом:

Является ли полным метрическим пространством?

.

Я понимаю, что необходимо воспользоваться теоремой:

«Метрическое пространство называется полным, если в нём всякая фундаментальная последовательность сходится.»

Однако я не совсем представляю себе доказательство сходимости любой последовательности из представленного нам пространства.

Я разобрал следующий пример, что был приведён на лекции:

«Является ли полным метрическим пространством?»
.

Для доказательства была использована одна из аксиом метрики:

Добавили и отняли в первом модуле + воспользовались свойством, что модуль суммы меньше либо равен суммы модулей и получили следующее:

Записали определение фундаментальности для данной последовательности:
— фундаментальна когда тогда и только тогда, когда , что и , будет выполняться:

После этого обозначили и получили:

— сходится относительно этой метрики, тогда пусть . Отсюда при
, т.к. и
Значит,

Не могу провести аналогичные рассуждения в примере, который привёл первым, т.к. меня смущает , ну и, собственно, доказательство верности аксиомы метрики для максимумов.

Заслуженный участник

Последний раз редактировалось ewert 25.09.2012, 14:39, всего редактировалось 1 раз.

Последний раз редактировалось ARD_ElEcTrO 25.09.2012, 17:53, всего редактировалось 3 раз(а).

ewert
А не могли бы вы поподробнее объяснить? Я так понимаю, что последовательность фундаментальна в пространстве с данной метрикой, если при , стремящимся к бесконечности независимо друг от друга, будет стремится к нулю. Однако, как действовать, когда у нас есть ?

Допустим, взяли мы первый модуль . Разложили. Вторая скобка всегда положительна и будет стремится к бесконечности, при стремлении n к бесконечности. А вот о первой однозначно ответить нельзя. Я в замешательстве.

Заслуженный участник

Последний раз редактировалось ARD_ElEcTrO 26.09.2012, 00:26, всего редактировалось 1 раз.

По-моему, уловил мысль:

Рассматриваем по отдельности:

, так как вторая скобка всегда положительна, а первая будет стремиться к нулю, так как разность и будет стремится к нулю при и при . Итого, последовательность по иксам окажется фундаментальной.

Аналогично по игрекам.

Значит, после этого можно утверждать, что любая последовательность из будет фундаментальна, следовательно, полнота метрического пространства доказана.

Верно ведь? Это достаточно исчерпывающе?

Последний раз редактировалось ARD_ElEcTrO 16.10.2012, 13:15, всего редактировалось 1 раз.

Последний раз редактировалось involume 18.03.2013, 20:39, всего редактировалось 6 раз(а).

Можете, пожалуйста, по подробнее объяснить с того момента, когда мы начинаем доказывать полноту метрического пространства? Понятно, когда доказывается метрика, там 3 аксиомы, 2 из которых тривиальны и лишь по сути третья (неравенство треугольника) требует доказательства. Но так как там модули, то всё становится до банального легко.

Просто чудом повезло, что задание такое же, . Вернее, полностью оно звучит так: «Можно ли задать метрику на вещественной прямой с помощью ? Если да, то будет ли получившееся метрическое пространство полным? «.

На первое я ответил, метрику задать можно, т.к. выполняются все 3 аксиомы. А вот с доказательством полноты у меня как-то не идёт ;-(

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

II. Основные теоремы о пространствах

2.1. Полные метрические пространства

Теорема 1 (Критерий полноты Кантора). Метрическое пространство полно, если и только если любая последовательность непустых вложенных замкнутых шаров, радиусы которых стремятся к нулю, имеет непустое пересечение.

Необходимость. Пусть последовательность вложенных шаров при r_{n →∞}→0 и пространство (X,ρ) полное. Тогда существует и единственна точка x₀, принадлежащая всем шарам сразу. Рассмотрим последовательность n> центров этих шаров и оценим расстояние ρ(x_n,x_m) при m>n. Так как при , но по условию теоремы r_n→0, стало быть и ρ(x_n,x_m)→0 при n,m→∞. То есть последовательность n> фундаментальна и в силу полноты пространства сходится. Члены её, начиная с m-го, принадлежат шару так как шар замкнутый, то и предел принадлежит этому шару, а то есть пересечение шаров не пусто.

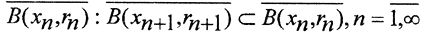
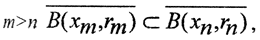
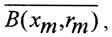
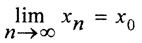
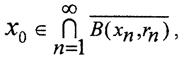
Пример. Может ли в банаховом пространстве иметь пустое пересечение последовательность непустых вложенных замкнутых множеств?

Да, может. Рассмотрим банахово пространство вещественных чисел R и последовательность непустых замкнутых вложенных множеств в нем x_i = [i,∞), i=1,∞. Ясно, что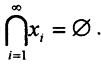

Пример. Множество рациональных чисел есть множество I категории.

Теорема 2 (Теорема Бэра о категориях). Носитель X полного метрического пространства (X,ρ) есть множество II категории.

( Комментарий. Ясно, что в полном метрическом пространстве всякое не пустое открытое множество есть множество второй категории, а множества, дополнительные к множествам первой категории, тоже множества второй категории.)

Определение 2. Полное метрическое пространство (Y,ρ_y) называется пополнением метрического пространства (X,ρ_x), если пространство (X,ρ_x) всюду плотно в пространстве (Y,ρ_y).

Определение 3. Пространства (X,ρ_x) и (Y,ρ_y) называют изомерными, если между ними существует хоть одна биекция и ρ_y = ρ_x.

Теорема 3 (Теорема Хаусдорфа о пополнении метрических пространств). Любое неполное метрическое пространство (X,ρ_x) имеет единственное с точностью до изомерности пополнение.

1. Из элементов данного неполного метрического пространства (X,ρ_x) построим некоторое пространство (Y,ρ_y).

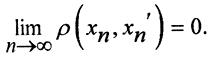
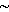
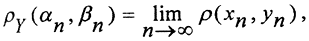
Фундаментальные последовательности n> и n> метрического пространства (X,ρ) назовём конфинальными, если Конфинальность определяет отношение эквивалентности x_nx’_n, то есть это отношение рефлексивно, симметрично и транзитивно. Рефлексивность и симметричность очевидны, а из неравенства треугольника следует транзитивность. Действительно, пусть x_nx’_n, а x’_nx»_n. Тогда ρ(x_n,x»_n)≤ρ(x_n,x’_n)+ρ(x’_n,x»_n). Если ρ(x_n,x’_n)→0 и ρ(x’_n,x»_n)→0, то ρ(x_n,x»_n)→0. Отношение эквивалентности разбивает фундаментальные последовательности пространства (X,ρ_x) на непересекающиеся классы эквивалентных между собой последовательностей. Таким образом мы получили новое фактор-множество Y, элементами которого являются непересекающиеся классы фундаментальных последовательностей <α_n>, <β_n>, <γ_n>. представителями которых являются фундаментальные последовательности n>, n>, n>. пространства (X,ρ_x). Если фундаментальная последовательность n> сходится к точке x, то и эквивалентная ей последовательность <α_n> сходится к той же точке. Действительно, пусть ρ(x_n,x)|_n→∞→0. Тогда ρ(α_n,x)≤ρ(α_n,x_n)+ρ(x_n,x)→0 и ρ(α_n,x)|_n→∞→0. Будем рассматривать фактор-множество Y как носитель нового метрического пространства (Y,ρ_y) с метрикой , если, конечно, удастся доказать, что это метрика.

2.1. Существование. Достаточно показать, что последовательность <ρ_n(x_n,y_n)> фундаментальна, тогда, в силу полноты числовой оси, она сходится. Полнота числовой оси доказывается независимо.

Лемма 1 (О четырёх точках). Для любых четырёх точек x,x’,y,y’ метрического пространства Х справедливо неравенство |ρ(x,y)-ρ(x’,y’)|≤ρ(x,x’)+ρ(y,y’).

ρ(x,y)≤ρ(x,x’)+ρ(x’,y)≤ρ(x,x’)+ρ(x’,y’)+ρ(y’,y) ⇒ ρ(x,y)-ρ(x’,y’)≤ρ(x,x’)+ρ(y,y’). Поменяв местами x,y и x’,y’, получим ρ(x’,y’)-ρ(x,y)≤ρ(x’,x)+ρ(y’,y).

Отсюда сразу |ρ(x,y)-ρ(x’,y’)|≤ρ(x,x’)+ρ(y,y’).

Лемма 2 (О непрерывности метрики). Метрика ρ(x,y) является непрерывной функцией своих аргументов.

Из леммы 1 |ρ(x_n,y_n)-ρ(x,y)|≤ρ(x_n,x)+ρ(y_n,y)→0 при n→∞, то есть если ρ(x_n,x)→0 и ρ(y_n,y)→0 при n→∞, то ρ(x_n,y_n)→ρ(x,y).

Доказательство существования метрического пространства (Y,ρ_y).

Если последовательности n> и n> фундаментальные, то ρ(x_n,x_m)→0 и ρ(y_n,y_m)→0 при m,n→∞. Тогда согласно лемме о четырёх точках можно записать соотношение: |ρ(x_n,y_n)-ρ(x_m,y_m)|≤ρ(x_n,x_m)+ρ(y_n,y_m)→0 при m,n→∞. То есть числовая последовательность <ρ_n(x_n,y_n)> фундаментальна и, следовательно, и сходится в полном пространстве R 1 ₁.

2.2. Доказательство независимости от выбора представителей.

2.3. Проверим выполнение аксиом метрики.

1. По свойствам пределов, связанных с неравенствами, если все члены последовательности <ρ_n(x_n,y_n)>≥0, то и

2. Симметричность очевидна.

3. Докажем аксиому треугольника. Так как ∀ n ρ(x_n,y_n)≤ρ(x_n,z_n)+ρ(z_n,y_n), то, по свойствам пределов, связанных с неравенствами и непрерывности метрики сразу получаем что и третья аксиома справедлива. Таким образом, пространство (Y,ρ_y) метрическое.

3. Покажем, что метрическое пространство (Y,ρ_y) и есть пополнение метрического пространства (X,ρ_x).

Надо показать, что: метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y) и эти пространства изомерны.

3.1. Покажем, что метрическое пространство (X,ρ_x) всюду плотно в метрическом пространстве (Y,ρ_y).

3.2. Покажем, что метрическое пространство (Y,ρ_y) полно.

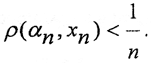
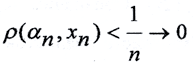
Рассмотрим некоторую фундаментальную последовательность <α_n>∈Y. Так как пространство (X,ρ_X) всюду плотно в (Y,ρ_y), то для каждого номера n найдётся элемент x_n∈X такой, что Тогда из неравенства треугольника следует соотношение ρ(x_n,x_m)≤ρ(x_n,α_n)+ρα_n,x_m) 1 ₁, то есть ρ_y(α₀,x_n)→0. Таким образом, метрическое пространство (Y,ρ_Y) полно.

3.3. Покажем, что метрическое пространство (Y,ρ_Y) является единственным с точностью до изоморфизма пополнением метрического пространства (X,ρ_X).

Источник