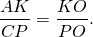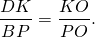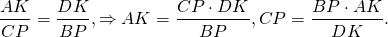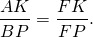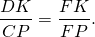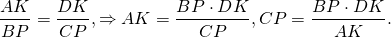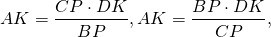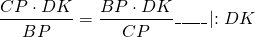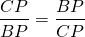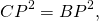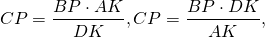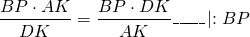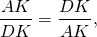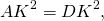Доказать что прямая проведенная через середины оснований трапеции

Замечательное свойство трапеции

Замечательное свойство трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

Дано:

ABCD- трапеция, AD||BC,

Доказать: K- середина AD,

Рассмотрим треугольники AOK и COP.

∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOK и COP подобны (по двум углам).

Аналогично, треугольники DOK и BOP подобны и

Так как правые части этих равенств равны, то левые также равны:

Рассмотрим треугольники AFK и BFP.

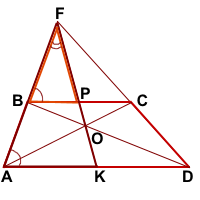
∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).

Следовательно, треугольники AFK и BFP подобны (по двум углам).

Аналогично, треугольники DFK и CFP подобны и

Правые части равенств равны, приравниваем левые части:

а значит, CP=BP, то есть P — середина BC.

AK=DK, K — середина AD.

Что и требовалось доказать.

В нашем случае докажем, что точки O и P лежат на прямой FK.

FK — медиана треугольника AFD.

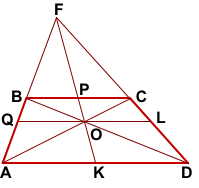
Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.

BC||AD (как основания трапеции), QL||AD (по построению).

Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.

Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.

Источник

Докажите что прямая проведенная через середины основания трапеций проходит через точку пересечения диагоналей трапеции и точку прододжения боковых сторон?

Докажите что прямая проведенная через середины основания трапеций проходит через точку пересечения диагоналей трапеции и точку прододжения боковых сторон.

Докажите что прямая проходящая чрез точку пересечения дигоналей равнобедреной трапеции и точку пересечения продолжения боковых сторон перпендикулярно основаниям трапеции и делит их пополам»?

Докажите что прямая проходящая чрез точку пересечения дигоналей равнобедреной трапеции и точку пересечения продолжения боковых сторон перпендикулярно основаниям трапеции и делит их пополам».

Докажите, что если точка пересечения диагоналей трапеции равноудалена от её сторон, то эта трапеция является параллелограммом?

Докажите, что если точка пересечения диагоналей трапеции равноудалена от её сторон, то эта трапеция является параллелограммом.

Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции?

Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.

Докажите, что точка пересечения диагоналей трапеции делит каждую диагональ на отрезки, пропорциональные основаниям трапеции?

Докажите, что точка пересечения диагоналей трапеции делит каждую диагональ на отрезки, пропорциональные основаниям трапеции.

Основания трапеции равны 3 и 91?

Основания трапеции равны 3 и 9

2. Найдите длину отрезка с концами на боковых сторонах трапеции, параллельного основаниям и делящего трапецию на две равновеликие части.

3. Найдите длину отрезка с концами на боковых сторонах трапеции, проходящего через точку пересечения ее диагоналей параллельно основаниям.

И желательно с чертежами пожалуйста)).

Прямая, параллельная основаниям МР и NK трапеции MNKP, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны MN и KP в точках A B соответственно?

Прямая, параллельная основаниям МР и NK трапеции MNKP, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны MN и KP в точках A B соответственно.

Найдите длину отрезка AB, если MP = 24см, NK = 16см.

Прямая, параллельная основаниям трапеции АВСD, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны АВ и СD в точках E и F соответственно?

Прямая, параллельная основаниям трапеции АВСD, проходит через точку пересечения диагоналей трапеции и пересекает её боковые стороны АВ и СD в точках E и F соответственно.

Найдите длину отрезка EF, если AD = 12см, ВС = 24см.

1))))))))))))))Дана трапеция ABCD?

Докажите, что OF = ОЕ, если точка О — точка пересечения диагоналей трапеции, а отрезок FE проходит через точку О параллельно основаниям трапеции ВС и AD.

2)))))))))))))))В равнобедренную трапецию, периметр которой равен 80, а площадь равна 320, можно вписать окружность.

Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

Прямая, параллельная основаниям AD и BC трапеции ABCD, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны AB и CD в точках E и F соответственно?

Прямая, параллельная основаниям AD и BC трапеции ABCD, проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны AB и CD в точках E и F соответственно.

Найти длину отрезка EF, если AD = 10см, BC = 15см.

СРОЧНО?

ПОМОГИТЕ Даны отрезок АВ и параллельно ему прямая А воспользовавший утверждением в задачи «докажите что прямая проведенная через середину оснований трапеции проходит через точку пересечение диогонали трапеции и тачку пересечение продолжение боковых сторон» разделите отрезок АВ пополам при помощи одной линейки

Если можно с чертежом = ).

Можно например так. Точку В поставь где хочешь.

Источник

Доказать что прямая проведенная через середины оснований трапеции

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.<2>^<○>$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.<3>^<○>$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.<4>^<○>$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.<5>^<○>$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.<6>^<○>$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.<7>^<○>$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.<8>^<○>$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.<10>^<○>$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.<11>^<○>$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«|\|«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.<12>^<○>$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

Источник

Нахождение разных доказательств как средство развития исследовательских способностей учащихся

Разделы: Математика

Важность подхода к одной и той же задаче с различных сторон подчеркивал в свое время еще Лейбниц (1646 – 1716), создатель (наряду с Ньютоном) дифференциального и интегрального исчисления. Вот перевод одного из его замечаний: «Сравнивая друг с другом два различных выражения, содержащих одно и то же количество, вы можете найти неизвестное; сравнивая друг с другом два различных вывода одного и того же результата, вы можете открыть новый метод».
Опыт показывает, что решение одной и той же задачи различными методами естественно вписывается в процесс проведения уроков-практикумов по решению задач. Такая работа, когда один ученик или группа учащихся докладывают на занятии свои решения определенной задачи, таит в себе богатые возможности развития их исследовательских способностей.

С первых уроков геометрии мы обсуждаем с учащимися разные способы доказательства одной и той же теоремы. На обобщающих уроках разбиваем учащихся на группы и предлагаем каждой группе доказать одну и ту же теорему разными способами, дав направление поиска доказательства. Например, теорему косинусов первая группа доказывает координатным методом, вторая – используя векторы, третья – применяя теорему синусов, четвертая – соотношения между сторонами и углами прямоугольного треугольника. После этого ученики сравнивают различные способы доказательств и определяют среди них наиболее привлекательный (играет роль краткость доказательства, неожиданный подход, наглядность, связь между различными темами школьного курса планиметрии и т. д.).

Решение одной и той же задачи различными методами дает возможность полнее исследовать свойства геометрической фигуры. При этом школьники, участвуя в проектной деятельности, обсуждают и лучше узнают специфику того или иного метода, его преимущества и недостатки перед другими. Решая задачу подходящим методом, иногда удается попутно «открыть» свойство фигуры, о котором в задаче ничего не говорится, или получить интересное обобщение задачи. Нередко найденный способ решения может быть в дальнейшем использован для решения более трудных задач. Таким образом, решение некоторых задач двумя или большим числом способов служит хорошим средством углубления знаний. Тем более что при этом учениками не только усваиваются новые методы решений, но и постигается связь между различными разделами математики.
Особенностью следующей задачи является то, что ее можно решать различными способами с опорой на новую теорию в процессе изучения всего курса планиметрии. Решая же ее разными способами при заключительном обобщающем повторении, учащиеся получают возможность увидеть планиметрию как единое целое.

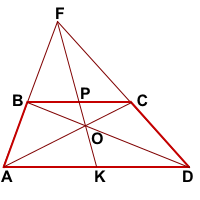
Задача 1. Докажите, что во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство 1. Используем утверждение: отрезок прямой, заключенный между боковыми сторонами трапеции и проходящий через точку пересечения диагоналей трапеции параллельно ее основаниям, делится этой точкой пополам.
1. Соединим отрезком точку пересечения продолжений боковых сторон трапеции Е и точку пересечения ее диагоналей О. ВСЕО = М, АDЕО = N. Докажем, что ВМ = МС и АN = ND (рис.1). Из этого и будет следовать, что середины оснований трапеции тоже лежат на той же прямой ЕО. По-другому говоря, переформулируем данную задачу так: доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений ее боковых сторон, делит основания трапеции пополам.

2. Предварительно через точку О параллельно основаниям данной трапеции проведем прямую, пересекающую ее боковые стороны АВ и CD в точках Р и Q соответственно, и докажем, что РО = ОQ. Действительно, ΔАОD

ΔВОС. Значит, . Прибавив единицу к обеим частям этого равенства, получим

. (1)

ΔOQD, следовательно, . Аналогично ΔВСА

ΔРOА и . Но согласно формуле (1). Отсюда следует: .
3. ΔANE

ΔРОЕ и, значит, . Аналогично . Отсюда получаем, что . Теперь уже видно, что из РО = ОQ следует, что АN = ND.
4. Точно также доказывается, что .

Замечание. Сделав два «шага», доказательство можно продолжить по-другому. После того, как доказано, что , имеем: середины оснований трапеции (М и N) и точка пересечения ее диагоналей (О) лежат на одной прямой. Действительно, все три указанные точки являются серединами отрезков прямых, проведенных параллельно основанию треугольника АDЕ, поэтому они принадлежат медиане этого треугольника, проведенной из вершины Е к основанию АD. Тем самым доказано, что Е, М, О и N лежат на одной прямой.

Доказательство 2. Используем признак подобия треугольников по двум углам.

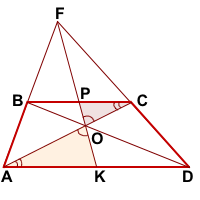
1. Соединим точки Е и О. Докажем, что ВМ = МС и АN = ND (рис.2).
2. Введем обозначения: ВМ = х, МС = у, АN = u, ND = v. Рассмотрим две пары подобных треугольников: ΔВМЕ

ΔNDE. Из подобия ΔВМЕ и ΔANE следует . Из подобия ΔМСЕ и ΔNDE следует . Значит,
3. Рассмотрим еще две пары следующих подобных треугольников: ΔВМО

ΔАОN.
Из подобия ΔВМО и ΔNОD следует . Из подобия ΔМОС и ΔАОN следует . Значит, .
4. Осталось решить систему уравнений:
Перемножим левые и правые части соответствующих уравнений:
, т. е. ВМ = МС. Так как , то , т. е. АN = ND.

Доказательство 3. Используем свойства векторов.

Докажем: 1) прямая, проведенная через середины оснований трапеции (точки M и N), проходит через точку пересечения продолжений боковых сторон (Е);

2) прямая MN проходит и через точку пересечения диагоналей трапеции (О).
1. Треугольники ЕАD и ЕСВ (рис. 2) подобны по первому признаку подобия треугольников, поэтому Так как и , то . Точка M – середина отрезка ВС, поэтому Аналогично Подставив в это равенство выражения для (), получим: = Отсюда следует, что векторы и коллинеарны, и, значит, точка Е лежит на прямой MN.
2. Для доказательства принадлежности точки О той же прямой MN, используем подобие треугольников АОD и СОВ. Имеем: . Из подобия треугольников АОD и СОВ: и = .Следовательно, векторы и коллинеарны, и, значит, точка О лежит на прямой MN.

Доказательство 4. Используем теорему Чевы.
1. К треугольнику АЕD, прямым АС, ВD и ЕN, проходящим через общую точку О (рис. 2), применим теорему Чевы:
2. По теореме Фалеса
3. Учитывая эти равенства, получаем: , т. е.
4. Так как , то , т. е. , следовательно, и ВМ = МС.

Доказательство 5. Используем параллельное проектирование.
Так как трапецию, данную в условии задачи, можно рассматривать как образ при параллельном проектировании любой трапеции, то будем считать, что проектируемая трапеция равнобедренная. У нее указанные точки лежат на одной прямой. Отсюда следует, что у нашей трапеции точки Е, М, О, N также лежат на одной прямой, так как при параллельном проектировании сохраняется принадлежность точек одной прямой, а также АN = ND и ВМ = МС (сохраняется отношение отрезков).
Обратим внимание, что каждый раз получается решение короче и красивее предыдущего.

Доказательство 6. Используем метод координат (рис. 2).
Середину N большего основания АD трапеции примем за начало аффинной системы координат, направленные прямые ND и NM – за оси координат. Пусть D(а; 0) и С (). Так как N и М – середины оснований АD и ВС трапеции и АD || ВС, то А(–а; 0), В(–). Вектор <а + >. Поскольку уравнение прямой, заданной точкой () и направляющим вектором записывается в виде , , то уравнение прямой АС (проходящей через точку А параллельно ненулевому вектору ) имеет вид: . Точно также составим уравнение прямой DВ: . Решив систему этих двух полученных уравнений, найдем координаты точки пересечения прямых АС и ВD: О. Отсюда видно, что точка О лежит на оси Оу, т. е. на прямой NM. Совершенно также докажем, что прямые АВ и DС имеют уравнения и , а точка их пересечения Е. Значит, точка Е также лежит на прямой NM.

Замечание. Задача 1 решена, но заметим, что систему координат можно было выбрать и по-другому. Например, точку Е принять за начало координат, а и − за координатные векторы. Точки N, M, E и О будут лежать на прямой у = х.
Решение задачи 1 возможно и с использованием гомотетии. Пусть AD:BC = k. Далее рассматривается гомотетия с центром в точке пересечения продолжений боковых сторон Е и с коэффициентом (−k). Таким образом, во взаимосвязанном мире планиметрии за одной задачей может скрываться очень многое.
Задача 2. Докажите теорему Птолемея: если четырехугольник ABCD вписан в окружность, то AC. BD= AB. CD+ AD. BC(произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон).

Доказательство 1. Используем подобие треугольников.

На рис. 3 изображен данный четырехугольник ABCD, его диагонали АС и ВD и описанная около него окружность.

Проведем из точки B отрезок BE до пересечения с диагональю AC таким образом, чтобы CBE = ABD Углы ÐBCЕ и ÐBDA равны как вписанные, опирающиеся на одну и ту же дугу AB. треугольники ABD и EBC подобны (по двум углам). Отсюда следует, что и, следовательно, имеем:

AD. BC= BD. CE. (2)

Подобны также треугольники ABE и DBC, так как ABE= DBCи BAE= BDC. Отсюда следует, что , и затем получаем:

AB. CD= BD.AE. (3)

Сложим соответственно левые и правые части равенств (2) и (3):
AD. BC+ AB. CD= BD. CE+ BD. AE = BD. (CE+ AE) = BD. AC, что и требовалось.

Замечание. К этому же можно прийти, введя другие обозначения. Если АВ = ВС = = СD = DА = АС = ВD = , то выберем на диагонали АС точку Е так, чтобы угол СВЕ был равен . Тогда треугольники СВЕ и DВА подобны. Поэтому ЕС:

Из подобия треугольников АВЕ и DВС (углы АВЕ и DВС равны как равносоставленные) получаем АЕ :
Значит, ЕС = АЕ = АЕ + ЕС =АС, отсюда

Доказательство 2. Используем теорему синусов.

Так как четырехугольник вписанный, то кроме входящих в условие теоремы величин целесообразно рассмотреть радиус круга R и углы четырехугольника. Введя углы, мы сможем использовать свойство вписанного четырехугольника. Итак, пусть и вписанные углы, опирающиеся соответственно на стороны АВ, ВС и АD (рис. 4). Тогда DВС = DАС = .
По теореме синусов
.

Следовательно,

Так как , то

=

Значит, .

Доказательство 3. Используем теорему косинусов.

Пусть АВ = ВС = СD = DА = АС = ВD = Докажем:
По теореме косинусов имеем: . Избавляясь от косинусов и раскладывая на множители, получаем:
,

.
Аналогично, .
Перемножив последние два равенства и произведя соответствующие сокращения, найдем: , откуда и следует требуемое.

Доказательство 4. Используем метод площадей.

Будем применять те же обозначения, что и в предыдущем доказательстве. Найдем площадь S четырехугольника АВСD двумя способами.

Площадь выпуклого четырехугольника равна половине произведения диагоналей на синус угла между ними: где угол между диагоналями.

Рассмотрим на дуге АВС (рис. 4) точку В´ такую, что АВ = СВ´. Поскольку треугольники АВС и СВ´А равны, то равны и их площади. Тогда равны площади четырехугольников АВСD и АВ´СD. Разобьем вновь полученный четырехугольник АВ´СD на два треугольника диагональю DВ´. Площадь треугольника АВ´D равна В´, площадь треугольника СВ´D равна В´. Так как четырехугольник АВ´СD вписанный, то углы DАВ´ и DСВ´ в сумме дают 180º и поэтоиу синусы этих углов совпадают. Остается заметить, что В´=В´ = по теореме об угле между пересекающимися хордами. Складывая площади треугольников и приравнивая результат к площади четырехугольника, получаем
, откуда , что и требовалось доказать.

Замечание. Та же идея может быть реализована по-другому. Покажем возникающие при этом нюансы.

Произведение диагоналей четырехугольника АВСD (рис. 5) равно площади этого четырехугольника S, деленной на 0,5 (как внешний угол треугольника ВОС). Остается показать, что и АВ · DС + ВС · DА = S : 0,5. Для этого заметим, что площадь четырехугольника АВСD не изменится, если треугольник ВСD «перевернуть», поменяв местами вершины В и D (рис. 6).Тогда После этого учтем, что в полученном четырехугольнике сумма противоположных углов равна 180º, т. е. º, откуда следует, что
и
АС · DВ = АВ · DС + ВС · DА.

Доказательство 5. Используем прямую Симпсона.

Определим такое понятие как педальный треугольник. Пусть Р – любая точка внутри треугольника АВС, и пусть перпендикуляры, опущенные из точки Р на его стороны ВС = , СА = =, АВ = будут .
Тогда треугольник , вершинами которого являются основания этих перпендикуляров, называется педальным треугольником точки Р относительно треугольника АВС
(например, треугольник с вершинами в точках касания вписанной окружности со сторонами данного треугольника – педальный треугольник центра вписанной окружности). Прямые углы в точках и (рис. 7) указывают на то, что эти точки лежат на окружности с диаметром АР; другими словами, точка Р лежит на окружности, описанной вокруг треугольника . Применяя теорему синусов к этому треугольнику, а также к самому треугольнику АВС, получим откуда

Рис.7

Аналогично, и

Таким образом, если расстояния от педальной точки до вершин треугольника АВС равны то длины сторон педального треугольника равны
Теперь рассмотрим тот особый случай, когда точка Р лежит на описанной окружности вокруг треугольника АВС (рис. 8). Тогда педальный треугольник «вырождается» в прямую, называемую прямой Симпсона. Хотя «педальный треугольник» вырожден, длины его «сторон» все еще могут быть вычислены с помощью формул: , , Так как , то , т. е. АВ · СР + ВС · АР = АС · ВР. Так как АВСР – вписанный четырехугольник, то теорема Птолемея доказана.

Доказательство 6. Используем преобразование, которое называется инверсией. Пусть задана некоторая окружность S с центром О и радиусом r (рис. 9).

Каждой точке Х, отличной от точки О, поставим в соот­ветствие точку Х´ на луче ОХ, такую, что ОХ´·ОХ = . Это преобразование и называется инверсией относительно окружности S.

Лемма (об инверсии). Пусть А´ и В´ − образы точек А и В при инверсии с центром О и радиусом r. Тогда треугольники ОАВ и ОВ´А´ подобны и (рис. 10).
Приведем рассуждения, доказывающие утверждение леммы. По определению инверсии выполняются равенства , .
Следовательно, , и поэтому

Значит, треугольники ОАВ и ОВ´А´ подобны (имеют общий угол при вершине О и их стороны, идущие от этой вершины, пропорциональны). При этом вершине А соответствует вершина В´, а вершине В – вершина А´. Но тогда и Из этого равенства Подставляя сюда выражение из определения , получаем Лемма доказана.

Итак, пусть четырехугольник АВСD вписан в окружность S (рис. 11)

По теореме об инверсии эту окружность инверсия I с центром в точке D (и любым радиусом) переведет в прямую p, не проходящую через точку D. Точки лежат на прямой p, причем точка лежит на отрезке . Поэтому . По лемме об инверсии . Подставив эти выражения в равенство , получаем:
АС · DВ = АВ · DС + ВС · DА, что и требовалось.

Приведенные доказательства на самом деле не исчерпывают всех возможных доказательств теоремы Птолемея. Укажем, что она может быть получена и как следствие теоремы Бретшнейдера (теоремы косинусов для четырехугольника), которая утверждает следующее: квадрат произведения диагоналей выпуклого четырехугольника равен сумме квадратов произведений его противоположных сторон без удвоенного произведения всех четырех сторон четырехугольника и косинуса суммы двух его противолежащих углов, т. е. , где угол, равный сумме углов А и С или В и D, так как . Поскольку во вписанном четырехугольнике сумма двух противоположных углов равна 180º, то по теореме Бретшнейдера в этом случае или , т. е. .
Из сказанного следует, что нахождение иного решения задачи всегда связано с дополнительным ее исследованием и, значит, при этом развиваются навыки школьников в исследовательской работе. Систематическое нахождение различных доказательств утверждений дает значительный эффект как при обучении решению задач, так и при обучении курсу математики в целом.

Источник