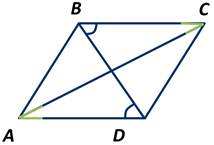
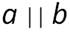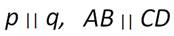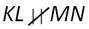Доказать что прямые параллельны если накрест лежащие углы равны

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

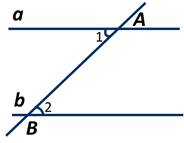
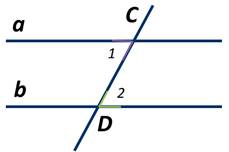
Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

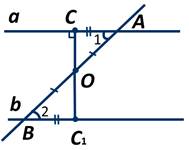
1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

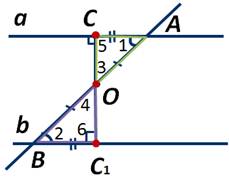
2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

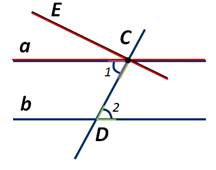
Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

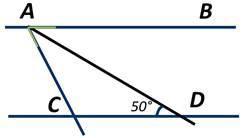
Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Ответ: AB║CD по 2 признаку параллельности прямых.

Источник

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов

Урок 13. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Параллельные прямые. Признак параллельности прямых по равенству накрест лежащих углов»

Две прямые называют параллельными, если они не пересекаются.

Параллельность прямых обозначают следующим образом:

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Например, отрезки АВ и CD параллельны, так как лежат на параллельных прямых p и q.

Параллельность отрезков обозначается:

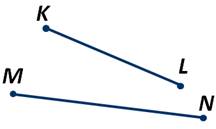
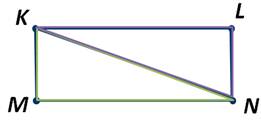
А вот если некоторые отрезки KL и MN не параллельны:

то обозначается так:

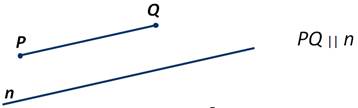
Параллельность двух лучей, отрезка и прямой, луча и прямой, луча и отрезка определяется аналогично. Например, отрезок PQ параллелен прямой n:

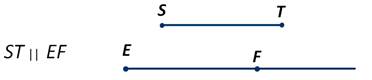
а отрезок ST параллелен лучу EF:

В геометрии нельзя «на глаз» определить, параллельны прямые или нет. Это может быть либо дано, либо доказано.

Известно, что две прямые, перпендикулярные к третьей, параллельны между собой.

Существует три признака параллельности прямых. Рассмотрим один из них:

Прямая c называется секущей по отношению к прямым а и b, если она пересекает каждую из них в разных точках.

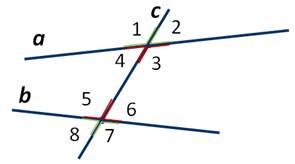
При пересечении прямых а и b секущей c образуется восемь углов.

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Пусть прямые а и b пересекает секущая АВ. И при этом накрест лежащие углы 1 и 2 равны.

Если ∠1=∠2=90 градусов, то прямая а перпендикулярна прямой АВ и прямая b перпендикулярна прямой АВ. А значит, прямая а параллельна прямой b.

А если ∠1=∠2, но они не являются прямыми, то из середины О отрезка АВ проведём отрезок ОС, который перпендикулярен прямой а. На прямой b отложим отрезок ВС₁=АС и проведём отрезок ОС₁.

Рассмотрим треугольники ОСА и ОС₁В. У них АО=ВО, АС=ВС₁, а ∠1=∠2. Следовательно, эти треугольники равны по первому признаку равенства треугольников.

Поэтому ∠3=∠4, а ∠5=∠6. Из равенства углов 3 и 4 следует, что точка С₁ лежит на продолжении луча ОС, то есть точки С, О, С₁ лежат на одной прямой. Так как ∠5=90 градусов, то из равенства углов 5 и 6 следует, что и ∠6=90 градусов.

Получаем, что прямая СС₁ перпендикулярна прямой а и перпендикулярна прямой b, а следовательно, прямая а параллельна прямой b. Что и требовалось доказать.

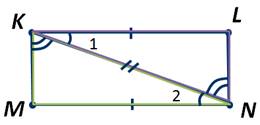
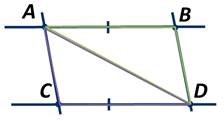
Доказать, что если два отрезка KL и MN равны и параллельны, то отрезки КМ и LN, соединяющие их соответственные концы, параллельны.

Проведём отрезок КN. И рассмотрим треугольники KMN и KLN.

Получаем, что треугольники KMN и KLN равны по первому признаку. Значит, углы LNK и MKN равны как углы, лежащие против равных сторон в равных треугольниках. Эти углы являются также накрест лежащими при прямых КМ и LN и секущей КN. А следовательно, отрезки КМ и LN параллельны. Что и требовалось доказать.

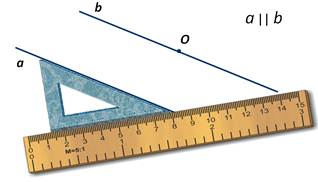
Чтобы построить прямую проходящую через заданную точку О и параллельную некоторой прямой а, приложим к прямой чертёжный угольник, а к нему линейку таким образом:

Затем будем продвигать угольник вдоль линейки, пока точка О не окажется на стороне угольника, и проведём прямую b. Прямые а и b будут параллельными, так как у них соответственные углы равны.

В черчении параллельные прямые можно построить с помощью рейсшины.

А вот при выполнении столярных работ для построения параллельных прямых используется малка, которая представляет собой две деревянные планки, скрепленные шарниром.

Источник

Параллельные прямые. Признаки параллельности прямых

Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Если прямые a и b параллельны, то это обозначают так:

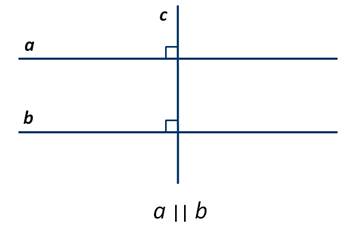
На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

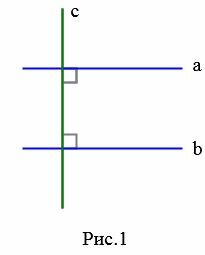Понятие параллельности можно распространять и на отрезки.

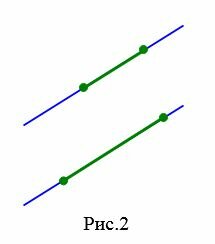Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

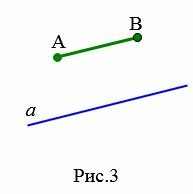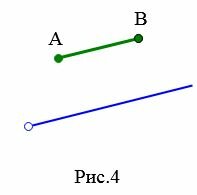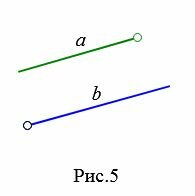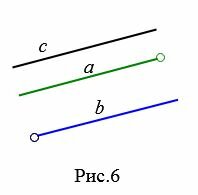На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

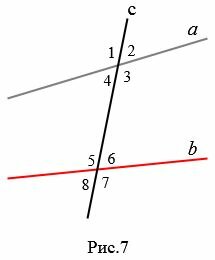Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

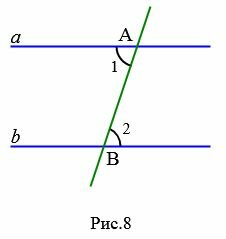Докажем, что .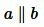

Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

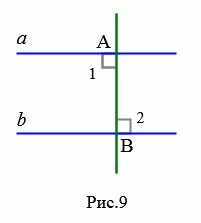Предположим, что углы 1 и 2 не прямые (Рис.10).

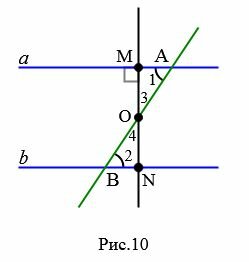Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

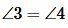
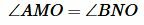
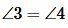
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

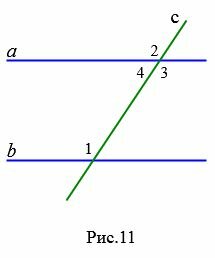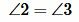
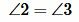
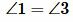
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

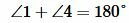
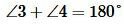
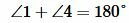
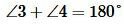
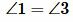
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

Источник

Теорема о равенстве накрест лежащих углов

Урок 17. Геометрия 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Теорема о равенстве накрест лежащих углов»

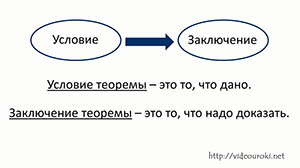
В формулировке любой теоремы можно выделить две части: условие и заключение. Условие теоремы – это то, что дано, а заключение – это то, что надо доказать.

Например, рассмотрим один из признаков параллельности прямых:

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Здесь условие утверждения: если при пересечении двух прямых секущей накрест лежащие углы равны. А заключение: прямые параллельны.

Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Пусть прямые а и b параллельны и пересечены секущей CD. Доказать, что накрест лежащие углы 1 и 2 равны.

Предположим, что углы 1 и 2 не равны. Тогда от луча CD отложим ∠ЕCD=∠2 так, чтобы ∠ЕCD и ∠2 были накрест лежащими углами при пересечении прямых СЕ и b секущей CD.

По построению эти накрест лежащие углы равны, а поэтому прямая CE параллельна прямой b. Получили, что через точку С проходят две прямые (а и CЕ) параллельные прямой b. А это противоречит аксиоме параллельности прямых. Следовательно, предположение неверно и угол ∠1=∠2. Что и требовалось доказать.

Прямые АВ и CD параллельны. Отрезок АВ=СD. Доказать, что прямая АС параллельна прямой BD.

Рассмотрим треугольник ABD и треугольник ACD.

То есть ∠CAD=∠BDA. А эти углы являются накрест лежащими при прямых AC и BD и секущей AD. Это означает, что прямые AC и BD параллельны. Что и требовалось доказать.

На рисунке ∠CBD=∠ADB. Доказать, что ∠ВСА=∠CAD.

∠ВСА и ∠CAD являются накрест лежащими при параллельных прямых AD и BC и секущей АС, а следовательно, они равны. Что и требовалось доказать.

Отметим, что если доказана какая-либо теорема, то это не означает, что обратная ей теорема верна.

Например, если углы вертикальные, то они равны. А вот если углы равны, то это ещё не означает, что они вертикальные.

Источник