Доказать что симметрическая разность коммутативна и ассоциативна

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Задача по алгебре 2

Супермодератор

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

Фундаментальная система циклов

По этой ссылке вы найдёте полный курс лекций по математике:

Термин фундаментальная система (решений) используется для обозначения базиса в пространстве решений системы линейных однородных (алгебраических) уравнений, либо в пространстве решений однородного дифференциального уравнения. В каждом из этих случаев через элементы фундаментальной системы оказывается возможным выразить, и при том единственным образом, элементы некоторого бесконечного множества. В (конечном) графе число циклов конечно, но может быть достаточно велико (по сравнению с порядком графа).

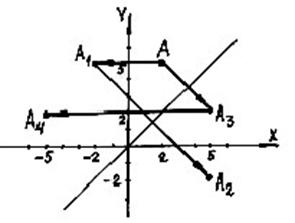
Симметрическая разность множеств Симметрической разностью множеств А и В называют множество Фундаментальная система циклов Операция нахождения симметрической разности коммутативна: А Д В = В Д А (это очевидно) и ассоциативна: (попробуйте доказать это с помощью рис. 22). В силу ассоциативности при записи симметрической разности нескольких множеств скобки (указывающие порядок выполнения данной операции над множествами) можно не расставлять. А АВ Рис. 22.

Симметрическая разность двух и трех множеств Пусть А — произвольное множество. Множество всех подмножеств А с операцией симметрической разности (/3(Л), Д) образует коммутативную группу; в роли нейтрального элемента группы выступает пустое множество, каждый элемент группы является обратным самому себе. Лемма 3. При произвольном натуральном п симметрическая разность п множеств состоит в точности из тех элементов данных множеств, которые принадлежат нечетному их числу.

Доказательство проводится индукцией по числу множеств. База индукция очевидна. Индукционный шаг. Пусть доказываемое утверждение справедливо для всех п ^ к. Симметрическая разность к + 1 множеств имеет вид причем p,q ^ к, p + q = k+1. Множество В состоит из элементов, принадлежащих В\ (значит, по индуктивному предположению, принадлежащих нечетному числу множеств из) и не принадлежащих Bi (то есть входящих в четное число множеств из или, наоборот, не принадлежащие В\ и принадлежат** В2 (т. е. принадлежащих четному числу множеств из А\. АР и нечетному числу множеств из Ар+1. yAp+q).

Возможно вам будут полезны данные страницы:

Оказывается, множество всех псевдоциклов графа замкнуто относительно симметрической разности.

Лемма 4. Для любого натурального п сиюлетринеская разность п псевдоциклов есть псевдоцикл. м Доказательство ведется индукцией по п. База индукции (утверждение для п = 1) очевидна. Обоснование индукционного шага сводится к рассмотрению случая двух псевдоциклов. Пусть С\ и — псевдоциклы. Для произвольной вершины v графа обозначим через S,(tj) множество ребер цикла С,, инцидентных v (t = 1,2). Степени вершины v в графах ) равны мощностям множеств S\(v), соответственно.

Множество всех циклов такого вида <Се \ е е Е \ Г>будем называть фундаментмьной системой циклов графа G = (V, Е) относительно стягивающего дерева (V,T). Пример см. на рис.23. Теорема 14. Произвольный цикл С связного графа G = (V,E) представим в виде симметрической разности некоторых циклов из фундаментальной системы циклов G относительно любого стягивающего дерева (V, Т). Такое представление единственно и имеет вид: Мы докажем даже более сильное угверждение, считая С псевдоциклом. Пусть — связный граф, (V, Т) — некоторое фиксированное стягивающее дерево G. Ребра этого дерева будем называть ветвями, а остальные ребра графа G — хордами.

Заметим, что каждый цикл Се содержит ровно одну хорду, а именно — е. Поэтому в симметрической разности (различных) фундаментальных циклов, равной С, должны присутствовать все циклы, отвечающие хордам из С\Г, и только они. Таним образом, если представление псевдоцикла С в виде симметрической разности фундаментальных циклов существует, то оно единственно и имеет вид (1). Докажем теперь, что равенство (1) действительно имеет место.

Пусть По лемме 4 В — псевдоцикл; как уже показано, из хорд В содержит только хорды, принадлежащие С. Применяя леммы 3 и 4, получаем, что симметрическая разность ВАС — псевдоцикл, не содержащий хорд (так как каждая хорда одновременно либо принадлежит, либо не принадлежит В и С, т. е. число се вхождений в данные два множества четно); стало быть, В АС СТ. Осталось доказать, что в В Л С нет и ветвей.

не пуст, то согласно следствию 4 теоремы 9 он имеет не менее двух висячих вершин, в то же время — по определению псевдоцикла — он не содержит висячих вершин. Итак, мы выяснили: 2? Д С = 0, что равносильно совпадению множеств В = Д Се и С. Теорема доказана. На множестве всех псевдоциклов связного графа можно ввести структуру линейного пространства над полем GF<2), где в роли «сложения» выступает симметрическая разность, а умножение на скаляр определяется естественным образом — для произвольного псевдоцикла С имеем:

Если электрической цепи сопоставить граф, ребра которого соответствуют источникам ЭДС, сопротивлениям, индуктивностям и т.д., а вершины — узлам соединений элементов цепи, то при использовании закона Кирхгофа для напряжений, гласящего: сумма падения напряжений вдоль цикла равна нулю, необходимо найти фундаментальную систему циклов. Уравнения, отвечающие этим циклам, не будуг зависеть друг от друга, в то же время их выполнение будет гарантировать выполнение уравнений для всех циклов графа.

Возможно эта страница вам будет полезна:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

> знак равно <\ Displaystyle

>

СОДЕРЖАНИЕ

Характеристики

А \ треугольник В \ треугольник С> 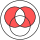△ <\ Displaystyle

> знак равно <\ Displaystyle

>

Симметричная разница также может быть выражена с помощью операции XOR ⊕ для предикатов, описывающих два набора в нотации создателя множеств :

Симметричная разница также может быть выражена как объединение двух множеств за вычетом их пересечения :

Из свойства инверсий в булевой группе следует, что симметричная разность двух повторяющихся симметричных разностей эквивалентна повторяющейся симметричной разности соединения двух мультимножеств, где для каждого двойного множества обе могут быть удалены. Особенно:

Пересечение распределяется по симметричной разнице:

К другим свойствам симметричной разницы относятся:

Эта операция имеет те же свойства, что и симметричная разность множеств.

Повторяющаяся симметричная разность в некотором смысле эквивалентна операции над мультимножеством множеств, дающей набор элементов, которые находятся в нечетном количестве множеств.

Как и выше, симметричная разность набора наборов содержит только элементы, которые находятся в нечетном количестве наборов в коллекции:

Симметричная разность на пространствах с мерой

Пока существует понятие «насколько велик» набор, симметричная разница между двумя наборами может считаться мерой того, насколько «далеко друг от друга» они находятся.

является псевдометрикой на Σ. d _μ становится метрикой, если Σ рассматривается по модулю отношения эквивалентности X

Расстояние Хаусдорфа против симметричной разности

Расстояние Хаусдорфа и (площадь) симметричной разности являются псевдометриками на множестве измеримых геометрических фигур. Однако они ведут себя совершенно иначе. На рисунке справа показаны две последовательности фигур: «Красный» и «Красный ∪ Зеленый». Когда расстояние Хаусдорфа между ними становится меньше, площадь симметричной разницы между ними становится больше, и наоборот. Продолжая эти последовательности в обоих направлениях, можно получить две последовательности, в которых расстояние Хаусдорфа между ними сходится к 0, а симметричное расстояние между ними расходится, или наоборот.

Источник

Ассоциативные и коммутативные операции

Ассоциативной бинарной операцией называется операция φ, если она обладает сочетательным свойством 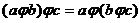. Ассоциативность позволяет записывать последовательность таких операций без скобок: aj bj c. Ср. в арифметике формулы a + b + c, abcd.

Примером ассоциативных операций служат объединение и пересечение множеств. Операция деления чисел не ассоциативна: (24 : 3) :4 = 2, тогда как 24 : (3 : 4) = 24 : 3/4 = 32. Также не ассоциативно вычитание (проверьте это). Поэтому для бесскобочной записи так называемой алгебраической суммы 20 – 5 –7 принято специальное соглашение: она означает (20 –5) –7, но не 20 – (5 –7), т.е. сложения и вычитания выполняются последовательно слева направо.

Коммутативной бинарной операциейназывается операция, обладающая свойством перестановочности: aj b = bj a.

Пример. Коммутативны сложение и умножение чисел, сложение и скалярное умножение векторов, объединение и пересечение множеств симметрическая разность множеств. Тем же свойством обладает сложение (т.е. последовательное выполнение) поворотов плоскости вокруг начала координат. Некоммутативными операциями над числами являются вычитание и деление
(a – b ≠ b – a, a/b ≠ b/a); некоммутативна разность множеств (A\B ≠ B\A).

Упражнение.Определите, для каких пар нижеследующих операций над предметами туалета их последовательное применение перестановочно: «надеть пиджак», «надеть туфли», «надеть шапку», «надеть пальто», «надеть носки».

Ассоциативными и коммутативными являются операции max(X, Y) и min(X, Y) на множестве чисел; поэтому можно употреблять записи без скобок max(X, Y, Z, T), min(A, B, C); к тому же, например, min(A, B, C) = min(В, С, А).

Дистрибутивностьодной бинарной операции φ относительно другой операции ψ выражает распределительный закон, подобный арифметическому соотношению (a + b) · c = a · c + b · c. Свойством дистрибутивности в арифметике обладает умножение относительно сложения, но не обладает сложение относительно умножения: a · (b + c) = a · b + a · c, но a · b + c ≠ (a + c) · (b + c).

Дистрибутивность позволяет раскрывать скобки в формулах.

В операциях над множествами пересечение дистрибутивно относительно объединения:
(А È В) Ç С = (А Ç С) È (В Ç С). Верно и обратное: объединение дистрибутивно относительно пересечения: (А Ç В) È С = (А È С) Ç (В È С).

Изоморфизм двух алгебр сохраняет ассоциативность, коммутативность и дистрибутивность.

Система нескольких алгебраических операций на множестве при возможности их последовательного выполнения в различных сочетаниях образует рассмотренную выше порождающую процедуру. Так, различные вычисления, в том числе достаточно сложные, осуществляются с помощью четырех арифметических действий. Правила шахматной игры определяют возможные ходы, т.е. преобразования позиции на доске, так что разные последовательности ходов создают большое разнообразие шахматных партий.

Двоичная система счисления

Важно заметить, что как при сложении, так и при умножении каждый знак результата
зависит от знаков слагаемых/сомножителей, находящихся в том же разряде и правее, и не зависит
от старших разрядов (находящихся левее). Так, младший разряд результата является функцией
двух однозначных чисел – младших разрядов слагаемых/сомножителей. Второй справа разряд
есть функция четырех однозначных переменных – знаков двух младших разрядов
слагаемых/сомножителей и т.д.

2. Таким же образом, только много проще, устроена двоичная система счисления. Числа представляются словами в алфавите Ц₂= [0, 1], и например, 110100101₂= 2 8 + 2 7 + 2 5 + 2 2 + 2 0 =
= (256 + 128 + 32 + 4 + 1)₁₀= 421₁₀ (подстрочные индексы 2 и 10 обозначают, что одно число записано в двоичной, а другое – в десятичной системе). Вот двоичные представления нескольких первых натуральных чисел (в левом столбце – десятичные; в правом – двоичные):

Подобно тому, как в десятичной системе счисления целые степени основания
системы 10 записываются единицей с нулями, а число на 1 меньшее – 99. 9, в двоичной системе число 10. 0 с k нулями изображает число 2 k (2, 4, 8, 16. ), а число 11. 1 из k единиц
равно 2 k – 1 (1, 3, 7, 15. ).

Таблица сложения для двоичных чисел чрезвычайно проста:

0 + 0 = 0; 0 + 1 = 1 + 0 = 1; 1 + 1 = 10.

Таблица умножения еще проще: .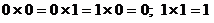

Их можно представить и таблицами с двумя входами:

Отсюда – простота действий над многозначными числами, хотя двоичная запись числа длиннее десятичной более чем втрое. Предыдущий пример демонстрирует перевод двоичного числа в десятичное. Для этого, так же как и для обратного перехода, полезно знать значения шкалы целых степеней числа 2: 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 и т.д. Каждое целое число можно однозначно представить в виде суммы различных целых степеней числа 2.

Как видим, сложение, вычитание и умножение многозначных двоичных чисел производится так же, как и десятичных, в частности, в обеих системах k-й знак результата арифметических действий зависит от k-х знаков слагаемых (соответственно, сомножителей) и знаков младших разрядов. Однако накопление знаков переноса при сложении возникает здесь значительно чаще: каждые две единицы дают перенос одной единицы в следующий – старший – разряд, сложение четырех единиц дает две единицы переноса, т.е. перенос одной единицы на два разряда влево.

Деление двоичных чисел «столбиком» также намного проще, чем в десятичной системе, поскольку не приходится подбирать очередной знак частного: остаток не должен быть меньше делителя, – в этом случае знак частного 1; в противном случае, как и для десятичных чисел, он равен 0, и нужно приписать к остатку (снести) очередной разряд делимого.

Среди алгебраических операций над двоичными векторами можно выделить поразрядные операции, например, поразрядное умножение: k-й знак результата равен произведению k-х знаков сомножителей. Другая операция – поразрядная сумма по модулю 2: k-й знак результата равен остатку от деления на два обычной арифметической суммы k-х знаков слагаемых.

Таблица этой операции для однозначных двоичных чисел a Å b:

Значения a Å b равны 1, если ровно одно из слагаемых равно 1, т.е. если оба слагаемых различны, и равны 0, если оба слагаемых одинаковы.

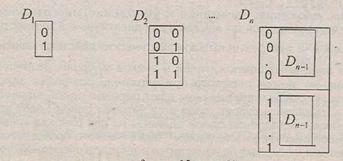
Таблица D_n, строки которой суть наборы из 0 и 1 длины n, может быть построена по индуктивному правилу (рис. 3.3):

1) таблица D₁ – это столбец из двух однозначных чисел 0 и 1;

Проценты

Три основные задачи на проценты таковы.

Задача 1. Найти указанный процент данного числа a.

Для этого данное число умножается на число процентов; результат делится на 100, то есть
р% от числа а составляет х = .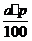

Задача 2. Найти число по заданной величине b и указанному ее проценту p.

Для этого заданная величина делится на число процентов; результат умножается на 100, то есть если р% от х равно b, то х = .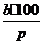

Задача 3. Найти выражение одного числа a в процентах от другого числа b.

Для этого умножаем первое число на 100, результат делим на второе число, то есть а составляет 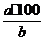% от b.

Указания. При решении задач на проценты необходимо твердо помнить, что:

1) при нахождении нескольких процентов от числа данное число принимается за 100%;

2) при нахождении числа по данным его процентам искомое число принимается за 100%;

3) при нахождении процентного отношения двух чисел за 100% принимается то число, с которым сравнивается другое.

Пример 1. На товар снизили цену сначала на 15%, а через год еще на 12%. Какова теперь цена товара, если до первого снижения цен он стоил 18000 руб.?

Пример 2. Цена на товар понизилась на 40%, затем возросла на 25%. На сколько процентов изменилась цена товара по сравнению с первоначальной ценой?

Решение. Обозначим через а первоначальную цену товара. Тогда после первого снижения цена товара будет равна а • (1-0,4) = 0,6а. После второго изменения новая цена будет равна
0,6а • (1+0,25) = 0,75а. Значит, цена товара после двукратного изменения уменьшилась на величину а – 0,75а = 0,25а, что составляет 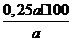% = 25% (см. задачу 3).

Пример 3. Первое число составляет 40% от второго. Сколько процентов от первого числа составляет второе?

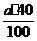
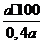
Решение. Пусть а – первое число. Тогда второе число будет равно = 0,4а (см. задачу 1). Значит, второе число от первого составляет % = 250% (см. задачу 3).

Пример 4. Первое число на 25% больше второго. На сколько процентов второе число меньше первого?

Решение. Второе число обозначим через а. Тогда первое число будет равно
а • (1+0,25) = 1,25а (см. задачу 1). В то же время второе число меньше первого на величину
(1,25а – а) = 0,25а. Как следует из задачи 3, она составляет 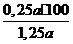% = 20%.

При многоэтапном начислении банковских процентов могут применяться две схемы. Схема простых процентов представляет собой процесс, при котором сумма вклада возрастает на каждом этапе на одно и то же количество процентов по отношению к первоначальному значению S₀. При этом она возрастает на одну и ту же величину, т.е. изменяется в арифметической прогрессии с разностью прогрессии d и соотношением S_n+1 = S_n + d.

В схеме сложных процентов величина возрастает на каждом этапе на одно и то же количество процентов по отношению к предыдущему значению S_n, т.е. в одно и то же число раз, и изменяется в геометрической прогрессии со знаменателем прогрессии q и соотношением b_n+1 = b_n • q.

Пример. Если банк начисляет ежегодно 10% на вклад 3000 руб. по схеме простых процентов, то первоначальная сумма будет последовательно принимать значения 3300, 3600, 3900, 4200. (разность прогрессии равна 300 руб.). По схеме сложных процентов она будет принимать значения 3300, 3630, 3993, 4392.3. (знаменатель прогрессии равен 1.1).

БИНАРНЫЕ ОТНОШЕНИЯ

Отношения на множествах

1. Одним из синонимов общего понятия соответствия является отношение.

Начнем с примеров. Натуральные числа могут быть полными квадратами, как 4, 81, 144, или не быть ими, как 5, 30, 48. Это свойство, или признак числа, можно трактовать как принадлежность к определенному подмножеству натуральных чисел – полных квадратов
<0, 1, 4, 9, 16, 25. >. То же можно сказать про признак «X > 2» для действительных чисел: число
5 обладает этим свойством, а число 1 – нет. Напротив, неравенство X > Y выражает свойство не одного числа X или Y, а совокупное свойство пары чисел: если X = 5, Y = 3, то неравенство выполняется, а для пар (5, 10) и (3, 5) не выполняется. Можно выразить это так: условие X > Y выполнено для определенного множества пар чисел.

Некоторые понятия как в математике, так и в обычном языковом употреблении самими своими названиями предполагают отношения между субъектами или объектами: сосед, знакомый (чей-то), одноименный, сопоставимый (с кем-либо или чем-либо), отличающийся (от чего-то другого), внутри, снаружи, между и др.

Таким образом, бинарное отношение – это свойство, присущее некоторым парам элементов
a Î M₁, b Î M₂. Обозначения бинарного отношения R(a, b) или aRb сходны с обозначением алгебраической операции, но результат отношения – выполнение или невыполнение свойства R. Можно также считать, что результат – множество тех пар (a, b), для которых свойство R выполнено.

Примеры: 1) бинарное отношение равенства между двумя числами, фигурами, множествами;

2) бинарное отношение старшинства между людьми по возрасту («старше», «моложе») или воинскому званию;

3) бинарные родственные и другие отношения между людьми: «быть отцом», «быть внуком», «быть одноклассниками», «быть одногодками»;

4) бинарное отношение C₇ между целыми числами – «иметь одинаковые остатки от деления на 7»;

5) отношение принадлежности элемента a множеству M, выполненное для всех таких пар
(a, M), что a Î M;

6) бинарное отношение инцидентности точки и прямой на плоскости или в пространстве: точка А лежит на прямой l.

Упражнение. 1) Определите, находятся ли в отношении C₇пары чисел: (12, 26), (16, 34), (34, 16), (26, 12);

2) в каком отношении из примера 2 находятся Л.Н. Толстой и И.С. Тургенев?

3) находятся ли в отношении инцидентности точка плоскости (4, 1) и прямая Y = X – 3?

Примеры. 1) Трехместное (тернарное) отношение «между» для тройки точек А, В, С на прямой: точка В расположена между точками А и С.

2) Тернарное отношение для тройки точек на плоскости – «лежать на одной прямой».

3) Четырехместное отношение для точек пространства – «принадлежать одной плоскости» (можно заметить, что трехместное отношение для точек пространства – «принадлежать одной плоскости» выполнено для любых трех точек).

4) Четырехместное отношение для четверки чисел X, Y, Z, T – «быть пропорциональными», т.е. удовлетворять соотношению X/Y = Z/T.

5) Тернарное отношение S(А, В, l) двух точек А, В и прямой l на плоскости – «точки А и В находятся по разные стороны от прямой l».

Источник