Доказать что супремум суммы множеств равен сумме супремумов

Теорема о существовании супремума

Выше было описано правило, устанавливающее признак равенства двух вещественных чисел. Опишем теперь правило, позволяющее установить, какое из двух вещественных чисел больше.

Пусть оба вещественных числа имеют знак +.

Найдем первую по порядку цифру в этих числах, которые не равны друг другу. Пусть это будет цифра с номером n, т.е.

(заметим,что символами математики это записывается так: 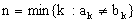). Тогда, если , то считаем, что a>b, а если , то a |b| то считаем, что а b.

Это правило будет необходимо нам ниже.

Определение. Множество, элементами которого являются вещественные числа, называется числовым множеством.

Для того, чтобы все дальнейшие определения и теоремы записывались в принятой математической форме, введем специальные значки, которые носят название кванторов. Их два:

Знакназывается “квантор общности” и читается “для каждого” ( есть перевернутая буква А из английского выражения “for All”).

Знак называется “квантором существования” и читается “существует” ( есть перевернутая буква Е из английского слова “Exist”). Вариантом этого квантора является знак!, который читается “существует единственный” или “существует один и только один”.

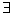
А теперь перейдем к определениям.

Определение 3. Числовое множество называется ограниченным, если .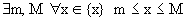

Определение 4. Наименьшая из верхних граней называется точной верхней гранью или супремумом числового множества (обозначение sup ).

Наибольшая из нижних граней называется точной нижней гранью или инфимумом числового множества (обозначение inf ).

Эти понятия столь важны, что опишем их в других терминах.

Sup определяется двумя свойствами:

Говоря образно, sup это планка, перепрыгнуть которую нельзя, но любая попытка опустить эту планку хоть чуть-чуть приводит к тому, что кто-то ее преодолевает.

Аналогично, inf определяется двумя свойствами:

Заметим, что сами sup и inf могут как принадлежать, так и не принадлежать множеству x.

Теперь мы в состоянии доказать важнейшую теорему этого раздела и одну из важнейших теорем всего мат. анализа.

Теорема о существовании супремума и инфимума.

Мы докажем эту теорему только для sup при одном дополнительном предположении – в множестве имеются положительные числа. Доказательство разбивается на три части.

а) Выбросим из множества все отрицательные числа.

б) У оставшихся чисел выпишем те цифры , которые стоят перед запятой. Множество этих цифр конечно, т.к. этих цифр не более чем [M] (целая часть М). Обратите внимание, что именно в этом месте используется ограничение теоремы – существование верхней грани. Если бы верхней грани не существовало, то множество было бы бесконечным.

в) Выбросим из все те числа, у которых цифра до запятой меньше. У оставшихся чисел выпишем первую цифру после запятой. Этих цифр не более 10. Выберем из них самую большую и обозначим ее через .

г) Выбросим из все те числа, у которых первая цифра после запятой меньше . У оставшихся чисел выпишем вторую цифру после запятой. Этих цифр не более 10. Выберем из них самую большую и обозначим ее через .

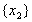
д) Выбросим из все те числа, у которых…

Повторяя эту операцию до бесконечности мы построим число

Возьмем любое . Если х имеет знак –, то ясно, что .

Пусть х имеет знак +. Тогда

Сравним . Вспомним, что было самым большим из . Поэтому может быть всего два варианта: либо , либо . В первом случае и дальнейшая проверка ни к чему.

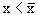
Если же , то сравним . Опять-таки по построению возможны два варианта: либо и тогда и дальнейшая проверка ни к чему, либо .

Если , то сравним. Опять-таки по построению возможны два варианта: либо и тогда и дальнейшая проверка ни к чему, либо .

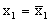
Продолжая этот процесс и дальше, получим, что возможны два следующих варианта.

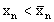
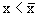
а) Найдется какое-то n, для которого . Тогда .

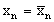
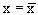
б) Для всех n . Тогда . Поэтому всегда и первое свойство супремума выполнено.

Проверка второго свойства супремума.

Заметим,что второе свойство можно записать так: . Возьмем положительное :

.

Так как , то найдется такое n,что

но вспомним процедуру построения. На n-м шаге после выбрасывания во множестве оставались лишь те числа, для которых . Любое из этих чисел будет больше x’ (т.к. ), но естественно, меньше или равно . Поэтому любое из этих чисел удовлетворяет второму свойству супремума. 

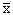
Подумайте сами, что надо изменить в процедуре построения, если во множестве есть только отрицательные числа.

Замечание. Все изложенные выше утверждения очевидным образом переносятся на понятие нижней грани.

Числовые множества: ограниченность, супремум, инфимум

2. Множество вещественных чисел называется ограниченным сверху (снизу), если существует число M ( m ) такое, что

1/AppData/Local/Temp/msohtmlclip1/01/clip_image002.gif” /> x £ M (1/AppData/Local/Temp/msohtmlclip1/01/clip_image034.gif» />то существует 1/AppData/Local/Temp/msohtmlclip1/01/clip_image058.gif” />, 1/AppData/Local/Temp/msohtmlclip1/01/clip_image062.gif” /> (или, что то же самое, * Если Слагаемое 1/AppData/Local/Temp/msohtmlclip1/01/clip_image058.gif” />, 1/AppData/Local/Temp/msohtmlclip1/01/clip_image078.gif” /> (или, что то же самое, * Если 1/AppData/Local/Temp/msohtmlclip1/01/clip_image058.gif” />, *1/AppData/Local/Temp/msohtmlclip1/01/clip_image105.gif” /> также и 1.Пусть функция f(x) непрерывна в точке x. Тогда производной где 1.Функция f(x) называется дифференцируемой в точке х, если ее приращение 1/AppData/Local/Temp/msohtmlclip1/01/clip_image134.gif» /> 1/AppData/Local/Temp/msohtmlclip1/01/clip_image139.gif» /> Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

На максимум модуля

— ограниченная область на комплексной плоскости. — голоморфны в .
.
Доказать, что если хотя бы одна функция не константа, то выполняется .

Нашёл принцип максимума модуля, что голоморфная функция достигает максимума модуля на границе области. Но там нужна непрерывность в замыкании области. А здесь её нет. Это как-то влияет или в принципе из максимума модуля всё и следует?

Заслуженный участник

Последний раз редактировалось thething 22.03.2018, 19:07, всего редактировалось 1 раз.

Непрерывность в замыкании нужна только для того, чтобы сказать, что максимум модуля достигается на границе. Если непрерывности в замыкании нет, то либо , либо ни в какой точке функция не может принимать максимального значения.
Можно сказать, что, при отсутствии непрерывности в замыкании в любой внутренней точке или , или

Подправьте индексы в формулах.

Какие? И, вроде, уже не могу.

Так на что тогда задача? Вроде, и так понятно, что если М достигается, то на границе, и для всех внутренних точек неравенство выполняется. А если не достигается, то

Заслуженный участник

Последний раз редактировалось g______d 22.03.2018, 20:47, всего редактировалось 1 раз.

Как минимум на то, к какой функции применить этот принцип максимума модуля. Если у меня правильное решение, то там нужно одно дополнительное действие.

Последний раз редактировалось MChagall 22.03.2018, 22:12, всего редактировалось 2 раз(а).

Вроде, что-то родилось.
Пусть . Эти либо не достигаются, либо достигаются на границе. То есть . Пусть . Тогда . А так как , то . Где-нибудь заблуждаюсь? Подозрительно просто.

Заслуженный участник

Заслуженный участник

Последний раз редактировалось g______d 22.03.2018, 22:59, всего редактировалось 1 раз.

Странный вопрос. Например, самому себе. Я вообще не знаю, равен ли он чему-то более простому. Ну вы хотя бы понимаете, где ошибка в процитированном равенстве? Собственно, неравенство очевидно (вы по сути его и доказали), но равенство совершенно не обязательно имеет место.

Заслуженный участник

Да. Именно супремум сумм. Для отдельных функций их супремумы реализуются, вообще говоря, в разных точках границы.

Заслуженный участник

Последний раз редактировалось g______d 23.03.2018, 01:07, всего редактировалось 1 раз.

У вас с индексами путаница. Насколько я понимаю, там нет никаких , а есть только . Функции разные, а одна и та же.

Рассмотрите сначала более простую задачу: если функции голоморфны в и непрерывны вплоть до границы, причём хотя бы одна из них не константа, то достигается только на границе .

Последний раз редактировалось MChagall 23.03.2018, 01:51, всего редактировалось 2 раз(а).

В задании так написано. Возможно, опечатка.

Заслуженный участник

Последний раз редактировалось g______d 23.03.2018, 05:37, всего редактировалось 1 раз.

Нет. Если у функции нет нулей, то и максимум, и минимум модуля достигаются на границе (достаточно применить принцип максимума модуля к ).

можно заменить на . Или ещё на что-нибудь. Или не , а .

Последний раз редактировалось MChagall 23.03.2018, 08:46, всего редактировалось 2 раз(а).

Имеете ввиду, что в качестве надо рассматривать линейные комбинации функций ? Каждая линейная комбинация достигает модуля на границе. Модуль одной из таких комбинаций равен сумме модулей, и, соответственно M (в вашей задаче) достигается только на границе. Верно всё?

Только что дальше? Чем отличается М исходной задачи, что там за предел?

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник