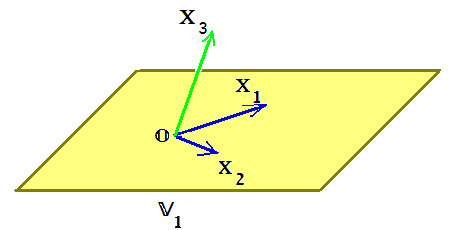
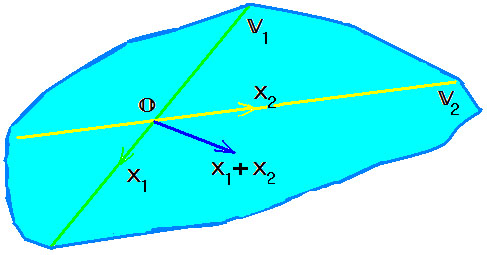
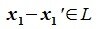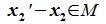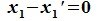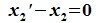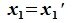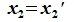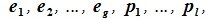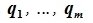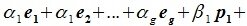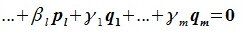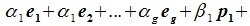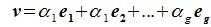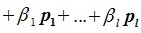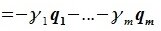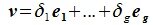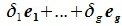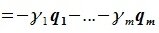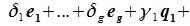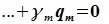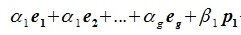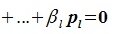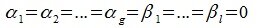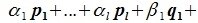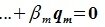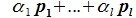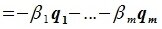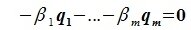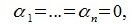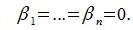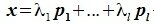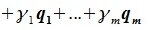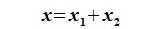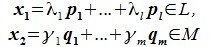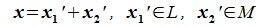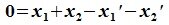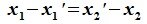Доказать что все симметрические матрицы образуют линейное подпространство

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Благодарю Ю.А.Смолькина за обнаружение 07.08.19 ошибки на настоящей странице и информирование о ней.

Линейное пространство

Определения

Примеры линейных пространств

Почему множество решений системы неоднородных уравнений не образует линейного подпространства?

В пространстве квадратных матриц фиксированного порядка каждое из следующих подмножеств составляет линейное подпространство: симметричных, кососимметричных, верхнетреугольных, нижнетреугольных и диагональных матриц.

Изоморфизм

Линейная зависимость, базис, координаты

Пример. Для полиномов нескольких переменных свойство линейной зависимости является частным проявлением более общего свойства функциональной зависимости. Так, однородные полиномы (формы)

Теорема 2. а) Если система содержит хотя бы один нулевой вектор, то она л.з.

б) Если система л.н.з., то и любая ее подсистема л.н.з.

Две системы векторов называются эквивалентными если каждый вектор одной системы линейно выражается через векторы другой и обратно.

Теорема 4. Системы векторов

Теорема 5. Если каждая из двух эквивалентных систем

Пример [1]. Замечательный пример трехмерного линейного пространства дает нам совокупность всех цветов. Под суммой двух цветов будем понимать цвет, образованный их смешением

Анимация ☞ ЗДЕСЬ (1500 K, gif)

Пример. Найти базис подпространства

Ответ. Базис составляют, например, первая, вторая и четвертая строки.

Найти координаты полинома

Критерии линейной зависимости

Относительный базис

Сумма и пересечение линейных подпространств

Понятие пересечения линейных подпространств совпадает с понятием пересечения их как множеств.

Теорема. Имеет место формула:

Доказательство ☞ ЗДЕСЬ.

Можно ли обобщить этот результат на случай трех (и более подпространств)? Cправедлив ли, к примеру, аналог формулы включений-исключений в следующем виде:

Теорема. Имеет место формула:

Пример. Найти базис суммы и размерность пересечения

Найти базисы суммы и пересечения подпространств

Решение ☞ ЗДЕСЬ.

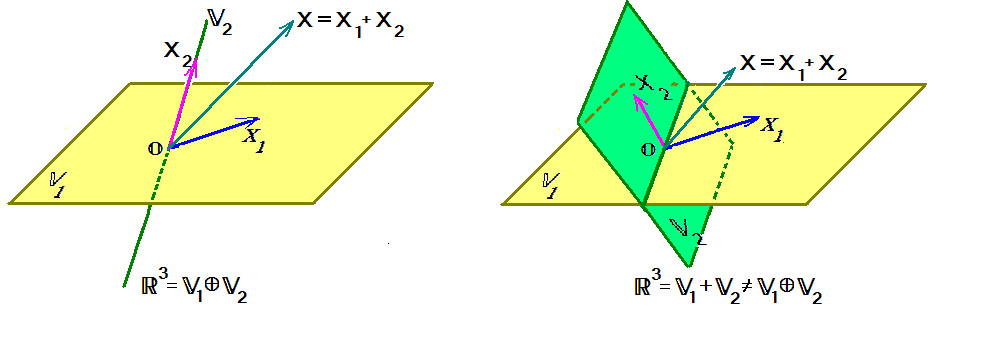
Прямая сумма линейных подпространств

Пример [2]. Доказать, что сумма подпространств

Линейные многообразия

Некоторые задачи на линейные многообразия ☞ ЗДЕСЬ.

Источник

Описание файла

Онлайн просмотр документа «Линейные Пространства»

Текст 3 страницы из документа «Линейные Пространства»

(все матрицы образуют динейно независимую систему).

2.21. Доказать, что матрицы вида образуют линейное подпространство в пространстве матриц М₂₃. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Линейность данного множества матриц следует из линейности операций умножения матриц на число и сложения матриц, например:

При этом каждая матрица данного подпространства может быть представлена в виде:

Для дополнения этого базиса до базиса всего пространства М₂₃ можно выбрать матрицы

(все матрицы образуют динейно независимую систему).

Проверяем линейность данного множества L матриц:

Все условия выполнены – L является линейным пространством.

т.е. матрица Х может быть представлена в виде:

2.23. Образуют ли матрицы базис в пространстве матриц М₂₂?

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно, данные матрицы не образуют базис в пространстве матриц М₂₂

2.24. Найти размерность и какой-нибудь базис линейной оболочки системы матриц

Запишем данные матрицы в каноническом базисе, получим векторы

найдем ранг этой системы векторов:

Ранг системы векторов равен 3, следовательно:

1) размерность данной системы матриц равна 3,

2) в качестве базиса их линейной оболочки можно взять первые три матрицы, т.е. (Е₁, Е₂, Е₃).

2.25. Установить, являются ли заданные множества подпространствами пространства M_nn. В случае положительного ответа найти базис и размерность подпространства.

1) множество всех симметрических квадратных матриц порядка n (A T = A).

3) множество всех квадратных вырожденных матриц порядка n (detA = 0).

3) Определитель суммы двух матриц, определители которых равны нулю, может быть отличен от нуля, например:

Следовательно, множество всех квадратных матриц порядка n, определитель которых равен нулю, не является подпространством пространства M_nn.

2.26. Доказать, что множество функций образует линейное пространство. Найти его размерность и базис.

Проверяем линейность заданного множества функций:

Все условия выполнены – L является линейным пространством.

2.27. Доказать, что множество функций образует линейное пространство. Найти его размерность и базис.

Проверяем линейность заданного множества функций:

Все условия выполнены – L является линейным пространством.

и любой вектор пространства L может быть представлен в виде линейной комбинации этих функций (по определению L), следовательно, эти функции образуют базис пространства L, размерность которого поэтому равна 3.

2.28. Исследовать на линейную независимость систему функций t, cost, sin2t>

Получили противоречие, из чего следует, что данная система функций является линейно независимой.

2.29. Исследовать на линейную независимость систему функций <1, lnt, ln2t>

Следовательно, данная система функций является линейно зависимой.

2.30. Исследовать на линейную независимость систему функций <1, cost, cos2t>

Получили противоречие, из чего следует, что данная система функций является линейно независимой.

Источник

Линейная алгебра, задачка на линейное подпространство

Выяснить, является ли подпространством линейного пространства V3 множество всех векторов x, удовлетворяющих условию: (x,a)=1, где a=(1,2,-1). Если да, то найти размерность этого подпространства.

Помогите пожалуйста, я знаю что такое линейно пространство, знаю что такое подпространства, знаю критерии (2 операции) по которым проверяется принадлежность векторов к подпространству. Знаю как находится размерность и.т.д. НО не могу додуматься как решить эту задачу, уже почти месяц не могу закрыться из-за этого, в методичках подобных задач не смог найти

Линейная алгебра. Линейная зависимость-независимость векторов
Являются ли вектора пространства L линейно независимыми? Если линейно зависимые, то выбрать из них.

Доказать, что векторы вида (a+b, b, 2a-b) образуют линейное подпространство
Доказать, что векторы вида (a+b, b, 2a-b) образуют линейное подпространство в пространстве R^3.

Доказать, что все симметрические матрицы образуют линейное подпространство
Доказать, что все симметрические матрицы образуют линейное подпространство пространства всех.

Значит, есть всё, что нужно, и нечего больше искать в методичках.

Значит, есть всё, что нужно, и нечего больше искать в методичках.

Не может быть так просто, у нас на контрольной целая серия таких задач. И не может она решаться так просто, ибо для чего-то же данны координаты вектора а.

Я сейчас попытался решить таким методом, как Вы считаете на скольк это правильно:

Выяснить, является ли подпространством линейного пространства V3 множество всех векторов x, удовлетворяющих условию: (x,a) =1, где a= (1,2,-1). Если да, то найти размерность этого подпространства.

Мы можем брать любой вектор x с координатами (X1;Y1:Z1) удовлетворяющий условию (x,a)=1
То бишь (X1*1 + Y1*2 – Z1*1) = 1

Пусть таким вектором x будет (1, 0, 0) подставим его – подходит. Ещё можно подобрать x(0,0,-1)

Далее попробуем сложить эти векторы получим (1,0,-1) подставим в условие и получим 2 (не равно единице) – пичаль. Т.е. получилось то-же что и при вашем решении.

При умножении на число, у нас получается, что вектор (1;0;0) и (0;0;1) мы можем умножить только на 1, иначе получится хрень неудовлетворяющая условие (или я напутал?).

То бишь это не подпространство. Ок.

Поставим условие так:

Выяснить, является ли подпространством линейного пространства V3 множество всех векторов x, удовлетворяющих условию: (x,a) =0, где a= (1,2,-1). Если да, то найти размерность этого подпространства.

Ну в данном случае в качестве x подойдёт вектор (-1,1,1), (-2,2,2), (-3,3,3) и.т.д.

В данном случае сумма двух любых из вышеперечисленных векторов удовлетворяет условию.

В случае проверки на это условие вашим методом должно получиться не 0, а 2. Т.е. это опять не подпространство что-ли?
Проверим умножение на число:
Тоже всё нормально, при любых значениях числа на которое мы умножаем условие выполняется.

Т.е. это подпространство линейного пространства, НО возникает вопрос – какова его размерность? Мне подсказали что 1, т.к. векторы линейно зависимы.

Источник

Подпространство линейного пространства

Определение и размерность подпространства

Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.

Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.

Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.

Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.

Сумма и пересечение подпространств

Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).

Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).

Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:

dim L+dim M=dim(L+M)+dim(L∩M).

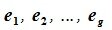
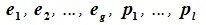
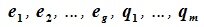
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис . Так как G⊂L и G⊂M, следовательно базис G можно дополнить до базиса L и до базиса M. Пусть базис подпространства L и пусть базис подпространства M. Покажем, что векторы

составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).

Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:

Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор

принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:

Из уравнений (6.4) и (6.5) имеем:

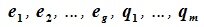
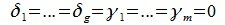
Но векторы являются базисом подпространства M, следовательно они линейно независимы и . Тогда (6.2) примет вид:

В силу линейной независимости базиса подпространства L имеем:

Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы

Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:

dim L+dim M−dim(L∩M)=dim(L+M). ■

Прямая сумма подпространств

Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.

Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.

Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.

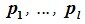
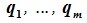
Доказательство. Выберем некоторый базис в подпространстве L и некоторый базис в подпространстве M. Докажем, что

является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:

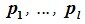
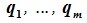
Но векторы и являются базисами подпространств L и M соответственно. Следовательно они линейно независимы. Тогда

Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.

Пусть x∈R. Разложим его по базису (6.11):

Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x₁∈L и x₂∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:

Вычитая (6.19) из (6.17), получим

Так как , и L∩M= 0, то и . Следовательно и . ■

Источник