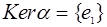Доказать что всякая подгруппа группы z имеет вид nz
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Задачи по алгебре
Последний раз редактировалось nou 27.06.2014, 15:09, всего редактировалось 1 раз.
| Заслуженный участник |
Последний раз редактировалось Xaositect 27.06.2014, 14:41, всего редактировалось 1 раз.
Вы не доказали, что все элементы этой подргуппы будут кратными 


Последний раз редактировалось nou 28.06.2014, 09:13, всего редактировалось 1 раз.
| Заслуженный участник |
Последний раз редактировалось Foxer 28.06.2014, 11:28, всего редактировалось 1 раз.
Бесспорно, тут это не нужно, но вот некоторые не любят доказательства от противного.
| Заслуженный участник |
Ни в коем случае. Ну то есть брать НОД можно, но потом придется доказывать, что он представляется линейной комбинацией некоторых элементов, а это по сути как раз наша теорема.
| Заслуженный участник |
Ну, я имел в виду такое рассуждение: раз у нас на каждом шаге НОД уменьшается, то рано или поздно нам придется остановиться. Не обязательно на единице.
А теперь попробуйте посностью написать аккуратное доказательство, которое сможет убедить инопланетянина, знакомого с понятиями группы, подгруппы и кольца 
| Заслуженный участник |

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Нормальные подгруппы. Факторгруппы.
Пусть 


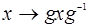
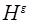
Подгруппа H называется инвариантной или нормальной в группе G, если все сопряженные подгруппы совпадают с ней самой: 
Равенство 
1. В коммутативной группе все подгруппы нормальны, так как отображение сопряжения в такой группе тождественно.
3. В рассмотренной выше группе 

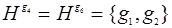

5. Подгруппа H индекса 2 нормальна. В самом деле, имеем 2 смежных класса : H и Hg = G-H = gH.
Теорема (свойство смежных классов по нормальной подгруппе).
Если подгруппа H нормальна в G, то множество всевозможных произведений элементов из двух каких либо смежных классов по этой подгруппе снова будет одним из смежных классов, то есть 
Очевидно, что для любой подгруппы H 

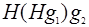


Таким образом, в случае нормальной подгруппы H определена алгебраическая операция на множестве смежных классов. Эта операция ассоциативна поскольку происходит из ассоциативного умножения в группе G. Нейтральным элементом для этой операции является смежный класс 

Гомоморфизм.
Отображение групп 


Таким образом, обобщение состоит в том, что вместо взаимно однозначных отображений, которые участвуют в определении изоморфизма, здесь допускаются любые отображения.
1. Разумеется, всякий изоморфизм является гомоморфизмом.
2. Тривиальное отображение 
3. Если 

4. Пусть 


5. По теореме С предыдущего раздела отображение сопряжения 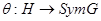
6. Отображение 
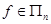


Теорема (свойства гомоморфизма)
Пусть 
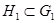

1. 

2. 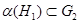
3. 

1. 

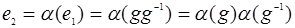
Нормальная подгруппа 


Гомоморфизм a инъективен тогда и только тогда, когда
Поскольку 



Понятие гомоморфизма тесно связано с понятием факторгруппы.
Теорема о гомоморфизме.
Любой гомоморфизм 
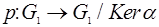


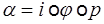
Пусть 



Циклические группы.
Таким образом, циклическая подгруппа с образующим элементом g является наименьшей подгруппой G, содержащей элемент g.
1. Группа Z целых чисел с операцией сложения является циклической группой с образующим элементом 1.
Теорема о структуре циклических групп.
Лекции по Линейной алгебре
Таким образом, циклическая подгруппа с образующим элементом g является наименьшей подгруппой G, содержащей элемент g.
Группа Z целых чисел с операцией сложения является циклической группой с образующим элементом 1.
Теорема о структуре циклических групп.
В самом деле, пусть 

Теорема о подгруппах конечной циклической группы.
Верна и обратная теорема: если конечная группа G порядка n обладает тем свойством, что для всякого делителя m числа n существует и притом ровно одна подгруппа H порядка m, то G — циклическая группа.
Будем говорить, что конечная группа G порядка N обладает свойством (Z), если для всякого делителя m числа N существует и притом только одна подгруппа H М G порядка m. Нам надо доказать, что всякая группа, обладающая свойством (Z) циклическая. Установим прежде всего некоторые свойства таких групп.
Если G обладает свойством (Z), то
Любая подгруппа G нормальна.
Если x и y два элемента такой группы и их порядки взаимно просты, то xy = yx.
Если H подгруппа порядка m такой группы G порядка N и числа m и N/m взаимно просты, то H обладает свойством (Z).
2. Пусть порядок x равен p, а порядок y равен q. По пункту 1) подгруппы Z(x) и Z(y) нормальны. Значит, Z(x)y = yZ(x) и xZ(y) = Z(y)x и потому для некоторых a и b 




11. Некоторые теоремы о подгруппах конечных групп.
Если порядок конечной группы делится на простое число p, то в ней имеется элемент порядка p.
Если некоторая факторгруппа G/H конечной группы G имеет элемент порядка p, то тем же свойством обладает и сама группа G.
Пусть 



Доказательство теоремы Коши.
Зафиксируем простое число p и будем проводить индукцию по порядку n группы G. Если n=p, то G » Z/pZ и теорема верна. Пусть теорема уже доказана для всех групп порядка меньше n и 
Рассмотрим последовательно несколько случаев
G содержит собственную нормальную подгруппу. Если ее порядок делится на p, то по 1 теорема доказана. В противном случае на p делится порядок факторгруппы G/H и теорема в этом случае следует из доказанной выше леммы.
Остается рассмотреть случай, когда порядки всех собственных подгрупп G не делятся на p, группа G проста ( то есть не имеет собственных нормальных подгрупп ) и не коммутативна. Покажем, что этого быть не может. Поскольку центр группы G является нормальной подгруппой и не может совпадать со всей группой, он тривиален. Поэтому G можно рассматривать как группу преобразований сопряжения на множестве G. Рассмотрим разбиение множества G на классы сопряженных элементов: 




Если число p не является простым, то теорема неверна даже для коммутативных групп. Например, группа 
Теорема о подгруппах коммутативной группы.
5rik.ru
Материалы для учебы и работы
Нормальные подгруппы
Определение 3.4.1. Пусть H – подгруппа группы G и 
Если существует 
Аналогично строятся правые смежные классы Ha = <h·a | h Î H> с представителями 
Теорема 3.4.1. Пусть H – подгруппа группы G. Тогда
1) каждый элемент 
2) два элемента 
3) любые два левых (правых) смежных класса либо не пересекаются, либо совпадают;
4) G есть объединение попарно непересекающихся левых (правых) смежных классов по подгруппе H.


3) Пусть c Î aH Ç bH Û для некоторых h1, h2 Î H c = a·h1 = b·h2 Û b –1 ·a = h2·h1 –1 Î H Û a, b принадлежат одному и тому же левому смежному классу согласно утверждению 2, то есть aH = bH.
4) Следует из утверждений 1 и 3.
Определение 3.4.2. Мощность множества всех различных левых (правых) смежных классов группы G по подгруппе H называется индексом подгруппы H в группе G и обозначается G : H.
К важнейшим в теории групп относится следующая теорема, доказанная известным французским математиком и механиком Жозефом Лагранжем (1736–1813).
Теорема 3.4.2 (Ж. Лагранж). Порядок конечной группы равен произведению порядка и индекса любой ее подгруппы.

Для » a Î G aH = <a, a·h2,…, a·hk>, Ha = <a, h2·a,…, hk·a>. Покажем, что | H | = | aH | = | Ha |. Действительно, a·hi = a·hj Û a –1 ·(a·hi) = a –1 ·(a·hj) Û hi = hj, аналогично hi·a = hj·a Û hi = hj для всех 
Согласно утверждению 4 теоремы 3.4.1 G есть объединение попарно непересекающихся левых (правых) смежных классов по подгруппе H. Таким образом, 
Следствие 1. Порядок конечной группы делится на порядок любой ее подгруппы.
Следствие 2. Если G – конечная группа порядка n, то порядок любого элемента группы делит порядок группы и для каждого 



Следствие 3. Любая группа простого порядка является циклической и не содержит собственных подгрупп.
По следствию 1 из теоремы 3.4.2 порядок любой подгруппы H в G равен 1 или p, то есть H = <e> или H = G.
Так как для произвольной группы (G, ·) и » a Î G, следуя доказательству теоремы 3.4.2, G « aG « Ga, то aG = G = Ga и G : G = 1.
Пример 3.4.1. Рассмотрим (nZ, +) £ (Z, +) для » n Î N и найдем все смежные классы Z по nZ. Поскольку (Z, +) – абелева группа, то для одинаковых представителей левые смежные классы совпадают с соответствующими правыми. Таким образом, для » z Î Z z = nq + r, где q, r Î Z, 0 £ r 4 = 16, | H | = 4, значит, V4(Z/2Z) : H = 16 : 4 = 4. Для одинаковых представителей левые смежные классы совпадают с правыми, поскольку (V4(Z/2Z), +) – абелева группа.
Выпишем таблицу 3.4.1 смежных классов группы (V4(Z/2Z), +) по подгруппе (H, +).
Таблица 3.4.1
| № | класс a + H | a + 0 | a + e1 | a + e2 | a + e3 |
| 1. | 0 + H = H |  |  |  |  |
| 2. |  + H + H |  |  |  |  |
| 3. |  + H + H |  |  |  |  |
| 4. |  + H + H |  |  |  |  |
Определение 3.4.3. Подгруппа H группы G называется нормальной, если для всякого 

Ясно, что у абелевых групп все подгруппы нормальны.
В любой группе (G, ·) тривиальные подгруппы <e> и G являются нормальными, так как для » a Î G a<e> = <a> = <e>a и aG = G = Ga. Итак, <e>

Пример 3.4.3. Если G : H = 2, то H
Теорема 3.4.3 (критерий нормальной подгруппы). H