Докажите что 22225555 55552222 делится на 7

Докажите, что 2222 в степени 5555 + 5555 в степени 2222 будет делится на 7?

Докажите, что 2222 в степени 5555 + 5555 в степени 2222 будет делится на 7.

Остаток будет в числе 2222 ^ 5555 + 2222 ^ 2222 = (317 * 7 + 3) ^ 5555 + (317 * 7 + 3) ^ 2222

Остаток будет в числе 3 ^ 5555 + 3 ^ 2222 = (728 + 1) ^ 925 * 3 ^ 5 + (728 + 1) ^ 370 * 3 ^ 2

Остаток будет в числе 3 ^ 5 + 3 ^ 2 = 252

Значит 2222 в степени 5555 + 5555 в степени 2222 будет делится на 7.

Докажите что хотя бы одно из них делится на три.

Делится ли число 10 в 2012 степени + 2012 на 6?

Делится ли число 10 в 2012 степени + 2012 на 6?

Число 6 2000 степени отнять число 3 в 2000 степени делится на 5 докажите это?

Число 6 2000 степени отнять число 3 в 2000 степени делится на 5 докажите это.

Докажите что 5 в 9 степени + 5 в 8 степени делится на 6?

Докажите что 5 в 9 степени + 5 в 8 степени делится на 6.

41 в 3 степени + 14 в 3 степени делится?

41 в 3 степени + 14 в 3 степени делится.

Докажите что число 10 в 40 степени минус 7 делиться на 3?

Докажите что число 10 в 40 степени минус 7 делиться на 3.

ОТДАЮ ВСЕ, ЧТО ЕСТЬ?

ОТДАЮ ВСЕ, ЧТО ЕСТЬ!

Источник

Материалы к урокам (теория и практика) по теме «Делимость чисел. Сравнения.» (8, 9, 10 класс).

Эту тему полезно рассмотреть после изучения делимости с остатком в классе с углубленным изучением математики. С помощью сравнений можно доказывать признаки делимости, делимость числовых выражений, находить остатки.

Вычитая одно равенство из другого, получаем:

Конечно, теоремы 2 и 3 верны для любого числа слагаемых или множителей.

Следствие 2. Рассмотрим некоторый многочлен с целыми коэффициентами:

Аналогично рассматриваются три оставшихся случая.

Докажите, что при любом целом n число n 2 + n четно.

Докажите, что ни при каком натуральном n число 3 n -1 не является точным квадратом.

Докажите, что ни при каком натуральном n числа 5 n +2 и 5 n -2 не являются точными квадратами.

Докажите, что ни при каком натуральном n числа 7 n +3, 7 n -1, 7 n -2 не являются точными квадратами.

Всякое целое число n дает при делении на 2 один из остатков 0, 1, т. е. имеет место одно из сравнений:

Всякое целое число n дает при делении на 3 один из остатков 0,1,2,-1,-2 т.е. имеет место одно из сравнений:

n≡0 (mod 3), n≡1 (mod 3), n≡2 (mod 3).

n 2 -1=2 2 -1=3≡0( mod 3) в этом случае число делится на 3.

Всякое целое число n дает при делении на 3 один из остатков 0,1,2

Первое утверждение, верно, получили остатки 0.

Всякое целое число n дает при делении на 3 один из остатков 0,1,2, т.е.

n≡0 (mod 3), n≡1 (mod 3), n≡2 (mod 3),

Второе слагаемое -5 a 3 b 3 делится на 5, т.к. имеет такой множитель

Всякое целое число n дает при делении на 3 один из остатков 0,1,2, т.е. имеет место одно из сравнений:

n≡0 (mod 4), n≡1 (mod 4), n≡2 (mod 4), n≡3 (mod 4)

Периодичность остатков при возведении в степень.

Рассмотрим последовательные степени числа 2:

и найдем, какие остатки дают эти числа при делении на 5. Для нескольких первых чисел эти остатки легко найти:

Умножая полученное сравнение опять на 2, находим:

Еще раз умножив, получаем:

2 7 ≡8 (mod 5)≡3 ( mod 5)

2 8 ≡12 (mod 5)≡2 ( mod 5) и т. д.

Таким способом можно быстро найти остатки от деления на 5 чисел вида 2 n (не вычисляя самих степеней).

Запишем то, что получается, в две строки, подписывая

под каждой степенью ее остаток от деления на 5.

Сразу же видно, что остатки периодически повторяются: после четырех остатков 2, 4, 3, 1 снова повторяются в том же порядке эти остатки, затем снова и т. д.

Рассмотрим еще один пример: остатки от деления степеней тройки на 7. Мы имеем:

Умножая полученное сравнение 3 2 =9≡2 (mod 7)на 3, затем еще на 3 и т. д., получаем:

3 4 ≡18(mod 7)≡4 ( mod 7),

3 5 =4∙3=5(mod 7) и т. д. Если мы продолжим эти вычисления, мы получим следующие две строки (где под каждым числом подписан его остаток от деления на 7):

И здесь наблюдается периодическое чередование остатков: после каждых шести остатков все повторяется сначала. Наконец, еще один пример: остатки от деления

степеней двойки на 48. Производя вычисления таким же образом, получаем следующие две строки (где под каждым числом подписан его остаток при делении на 48):

Доказанные утверждения находят применение при решении ряда задач.

Мы уже видели в примере 1, что 222 555 ≡ 6( mod 7).

Теперь посмотрим, как повторяются остатки степеней двойки при делении на 7 :

Найдите остаток от деления числа 7 100 +11 100 на 13.

Найдите остаток от деления числа 6 592 на 11.

Делится ли число на 10?

Найдите наименьшее натуральное число, начинающееся с цифры 7 и уменьшающееся впятеро от перестановки этой цифры в конец.

Источник

Докажите что 22225555 55552222 делится на 7

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .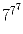

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник