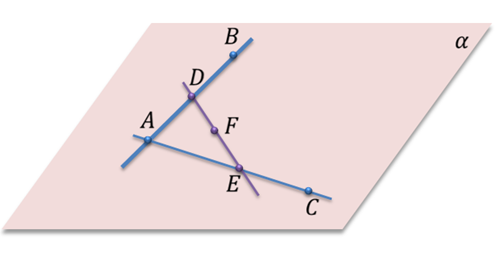
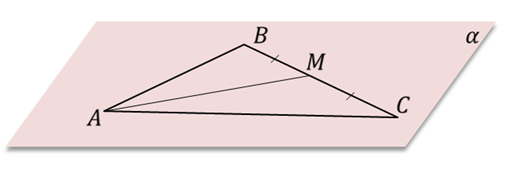
Докажите что через 2 пересекающиеся прямые проходит единственная плоскость

Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые

В данном материале мы расскажем, как правильно вычислить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые. Начнем с формулировки основного принципа, а потом, как всегда, разберем несколько задач, где можно применить этот принцип на практике.

Как найти уравнение плоскости, проходящей через пересекающиеся прямые?

Для того чтобы вывести это уравнение, нам понадобится вспомнить одну теорему. Она звучит так:

Через две пересекающиеся прямые может проходить только одна плоскость.

Доказательство этого утверждения основано на двух аксиомах:

В итоге мы можем утверждать, что с помощью указания двух пересекающихся прямых мы можем задать определенную плоскость в трехмерном пространстве.

Далее нам нужно доказать, что плоскость, которая проходит через две определенные прямые, совпадет с той, что проходит через три заданные точки, две из которых находятся на тех самых прямых.

Посмотрим на схему:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

Как найти уравнение плоскости, проходящей через параллельные прямые?

Для этого нам понадобится вспомнить теорему, которая формулируется так:

Через две параллельные прямые проходит только одна плоскость.

Ее можно доказать, используя аксиому о единственной плоскости, которая проходит через три точки, а также утверждение о двух параллельных прямых (если одна из параллельных прямых пресекает некоторую плоскость, то это же делает и другая).

Итак, возможно задать плоскость в пространстве, если указать две параллельные прямые, которые в ней находятся.

Очевиден тот факт, что плоскость, которая проходит через 2 параллельные прямые и плоскость, которая проходит через три точки, две из которой лежат на одной из этих прямых, будут совпадать.

После этого мы можем найти уравнение плоскости, проходящей через две заданные параллельные прямые.

Это и есть нужное нам уравнение плоскости, проходящей через заданные параллельные прямые.

Примеры задач на нахождение подобных уравнений

Таким образом, для того чтобы составить уравнение плоскости, которая проходит через 2 пересекающиеся или параллельные прямые, требуется вычислить координаты трех точек, которые расположены на этих прямых (две точки на одной прямой и третья на другой). Посмотрим, как это принцип реализуется на практике.

Решение

Возьмем более сложный пример, где координаты нужных точек не будут столь очевидными.

Составьте уравнение плоскости, которая проходит через них.

Решение

Для вычисления координат второй точки нам надо записать параметрическое уравнение:

Очевидно, что процесс вычисления координат нужных нам точек занимает больше всего времени при решении подобных задач.

Нам осталось разобрать пример плоскости, которая проходит через две прямые, являющиеся параллельными.

Решение

Источник

Некоторые следствия из аксиом.

Некоторые следствия из аксиом стериометрии. Решение задач.

Просмотр содержимого документа
«Некоторые следствия из аксиом.»

Некоторые следствия из аксиом:

Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости, т.е. (а, М) с α

2 . Любая плоскость проходящая через прямую а и точку М проходит через точки Р, О, и М, значит по аксиоме А1 она – единственная. Ч.т.д.

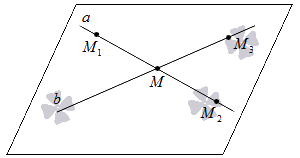
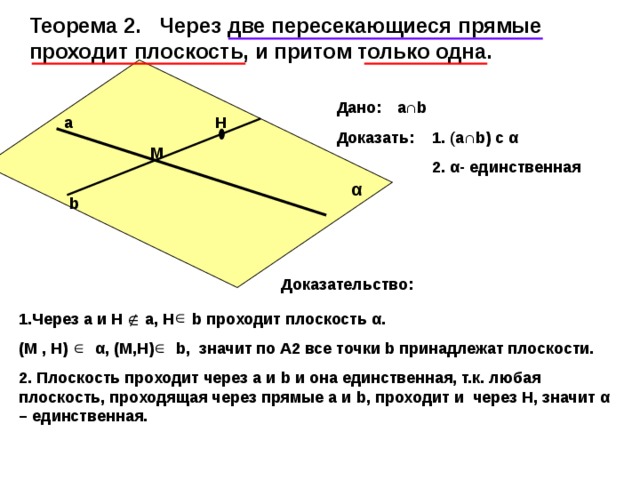
Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

1.Через а и Н а, Н b проходит плоскость α .

2. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b , проходит и через Н, значит α – единственная.

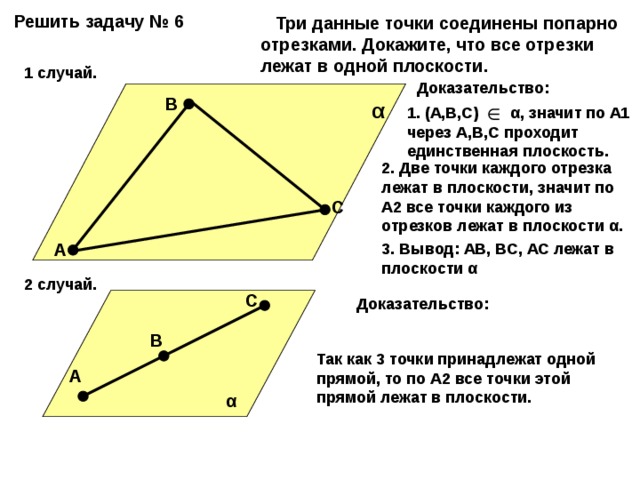
Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

1. (А,В,С) α , значит по А1 через А,В,С проходит единственная плоскость.

2. Две точки каждого отрезка лежат в плоскости, значит по А2 все точки каждого из отрезков лежат в плоскости α .

3. Вывод: АВ, ВС, АС лежат в плоскости α

Так как 3 точки принадлежат одной прямой, то по А2 все точки этой прямой лежат в плоскости.

Источник

Некоторые следствия из аксиом стереометрии

Урок 3. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Некоторые следствия из аксиом стереометрии»

На прошлом уроке мы с вами познакомились с аксиомами стереометрии. Давайте еще раз повторим их.

Первая аксиома звучит так: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Вторая аксиома звучит так: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Третья аксиома звучит так: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Сегодня на уроке мы сформулируем и докажем некоторые следствия из этих аксиом. По аналогии с аксиомами следствия мы будем обозначать заглавной буквой С с нижним индексом.

Итак, первое следствие звучит так: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

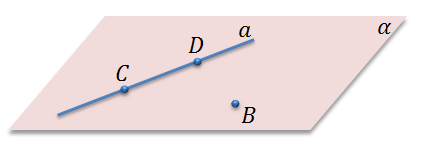
Докажем это. Рассмотрим прямую a и не лежащую на ней точку B. Нам необходимо доказать, что через прямую a и точку B проходит плоскость. Отметим на прямой a две точки C и D. Точки B, C, D не лежат на одной прямой, поэтому согласно первой аксиоме, (а именно, тому что через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна) через эти точки проходит некоторая плоскость α. Поскольку точки C и D прямой a лежат в плоскости, то по второй аксиоме (если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости) вся прямая a лежит в плоскости α.

Теперь давайте докажем единственность этой плоскости. Любая плоскость, которая проходит через прямую a и точку B проходит через точки B, C, D. То есть она совпадает с плоскостью α, поскольку по первой аксиоме, плоскость, которая проходит через три точки, не лежащие на одной прямой – единственная.

Теперь давайте сформулируем и докажем второе следствие.

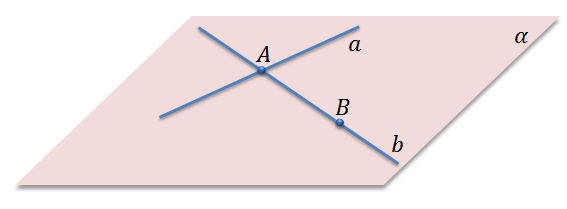
Через две пересекающиеся прямые проходит плоскость, и притом только одна.

Рассмотрим прямые a и b, которые пересекаются в точке А. Тогда нам необходимо доказать, что через эти прямые проходит плоскость, и притом только одна.

Отметим на прямой b точку B, не совпадающую с точкой А. Тогда из первого следствия, через прямую a и точку B можно провести плоскость α. Так как точки А и B прямой b лежат в плоскости α, то по второй аксиоме мы получим, что вся прямая b лежит в плоскости α. Поскольку через прямую и не лежащую на ней точку можно провести только одну плоскость, то значит, любая плоскость, проходящая через прямые a и b совпадает с плоскостью α.

Таким образом, наша теорема доказана.

Решим несколько задач.

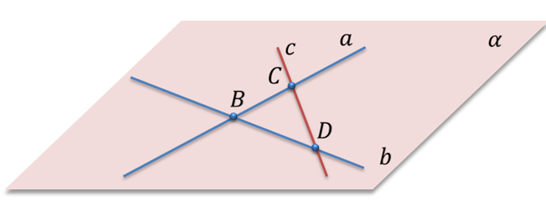
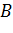
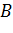
Задача. Две прямые пересекаются в точке . Доказать, что все прямые, которые пересекают данные прямые и не проходят через точку , лежат в одной плоскости.

По второму следствию из аксиом стереометрии через две пересекающиеся прямые проходит плоскость, и притом только одна. Значит, через данные прямые проведем плоскость альфа.

Проведем прямую, которая будет пересекать прямые, но не проходит через точку B. Эта прямая с каждой из данных прямых имеет по одной общей точке. Эти точки принадлежат построенной плоскости, поскольку прямые принадлежат этой плоскости. Получаем, что две точки прямой принадлежат плоскости, значит, по второй аксиоме, вся прямая лежит в этой же плоскости. Поскольку прямую мы проводили произвольно, то, очевидно, что каждая из прямых, которые будут пересекать исходные прямые будет лежать в этой же плоскости, что и требовалось доказать.

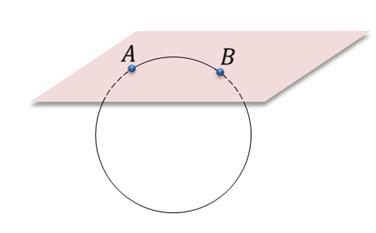
Задача. Верно ли утверждение: а) если две точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости; б) если три точки окружности лежат в плоскости, то и вся окружность лежит в этой плоскости?

Первое утверждение неверно, так как окружность и плоскость имеют две общие точки, если они пересекаются. То есть окружность не лежит в плоскости, а только пересекает ее.

Перейдем ко второму утверждению. По первой аксиоме через три точки, не лежащих на одной прямой можно провести плоскость и притом только одну. Точки окружности не могут лежать на одной прямой, поэтому проведем через них плоскость. Очевидно, что эти точки лежат в плоскости окружности, но поскольку аксиома говорит о том, что такая плоскость единственная, значит, окружность будет принадлежать этой плоскости. То есть второе утверждение верно.

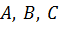
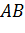
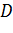
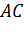
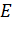
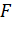
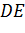
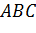
Задача. Пусть точки не лежат на одной прямой. Отметим на прямой точку , а на прямой – точку . Доказать, что точка прямой лежит в плоскости .

По первой аксиоме через точки А, B, C проведем плоскость α. Так как прямая АB лежит в плоскости α, значит, точка D лежит в плоскости α. Аналогично, поскольку прямая АC лежит в плоскости α, то и точка Е лежит в плоскости α. Получаем, что две точки прямой DE лежат в плоскости α. Применим вторую аксиому и получим, что вся прямая DE лежит в плоскости α. Тогда точка F прямой DE тоже лежит в плоскости α. Что и требовалось доказать.

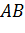
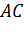
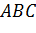
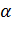
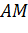
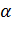
Задача. Пусть стороны и треугольника лежат в плоскости . Доказать, что и медиана лежит в плоскости .

Поскольку стороны AB и АC лежат в плоскости α, значит, точки B и C лежат в этой плоскости, то есть, по второй аксиоме, сторона BC тоже лежит в этой плоскости. Точка M лежит на прямой BC, значит, она лежит в плоскости α, что и требовалось доказать.

Подведем итоги урока. Итак, сегодня на уроке мы повторили аксиомы стереометрии, сформулировали и доказали некоторые следствия из аксиом и рассмотрели задачи, на использование аксиом и следствий из них.

Источник

Введение в стереометрию. Параллельность

Важные аксиомы стереометрии

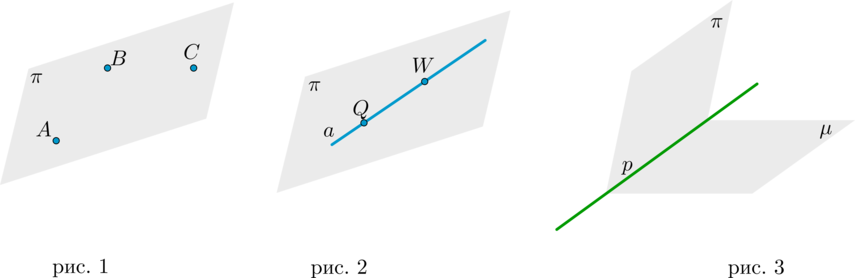
1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Таким образом, любая плоскость однозначно задается тремя точками, не лежащими на одной прямой: \(\pi=(ABC)\) (рис. 1).

Заметим, что плоскость обычно изображают в виде внутренности параллелограмма. Почему? Посмотрите, например, сбоку на стол. В виде какой фигуры выглядит столешница?

Следствия из аксиом

1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна (рис. 4).

2. Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 5).

Доказательство

Определения

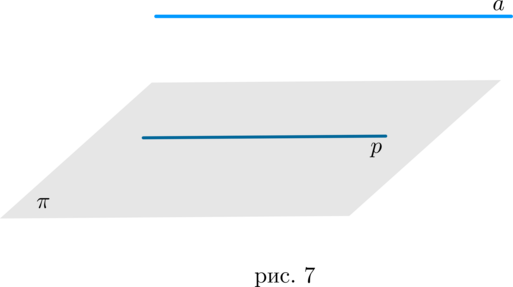
Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

Следствие 1

Через две параллельные прямые проходит плоскость, и притом только одна.

Теорема 1

Доказательство

Теорема 2

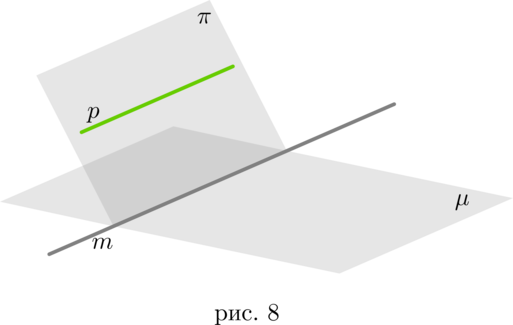
Если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.

Доказательство

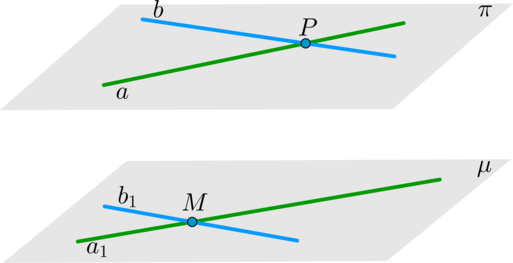
Теорема 3: о параллельности трех прямых

Доказательство

Определение

Существует три вида взаимного расположения прямой и плоскости:

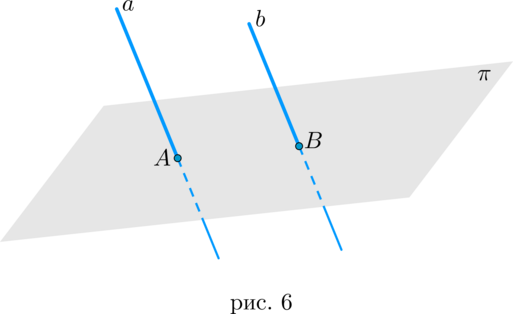
1. прямая имеет с плоскостью две общие точки (то есть лежит в плоскости) — рис. 4;

2. прямая имеет с плоскостью ровно одну общую точку (то есть пересекает плоскость) — рис. 6;

3. прямая не имеет с плоскостью общих точек (то есть параллельна плоскости).

Теорема 4: признак параллельности прямой и плоскости

Доказательство

Следствие 2

Доказательство

Следствие 3

Определение

Существует три типа взаимного расположения плоскостей в пространстве: совпадают (имеют три общие точки, не лежащие на одной прямой), пересекаются (имеют общие точки, лежащие строго на одной прямой), и не имеют общих точек.

Если две плоскости не имеют общих точек, то они называются параллельными плоскостями.

Теорема 5: признак параллельности плоскостей

Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.

Доказательство

Следствие 4

\[\alpha\parallel \beta, \ \alpha\cap \gamma=a, \ \beta\cap\gamma=b \Longrightarrow a\parallel b\]

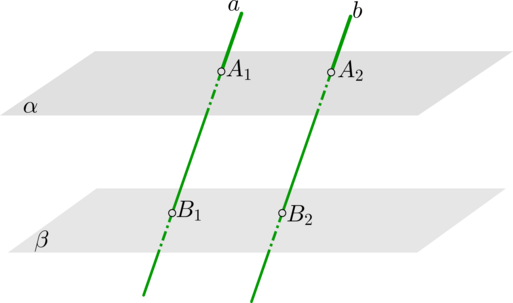
Следствие 5

Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны:

\[\alpha\parallel \beta, \ a\parallel b \Longrightarrow A_1B_1=A_2B_2\]

Источник

Стереометрия. Страница 1

1. Основные фигуры стереометрии

Аксиомы планиметрии описывают свойства простейших геометрических фигур на плоскости. Так как стереометрия изучает фигуры в пространстве и в пространстве может быть великое множество плоскостей, то аксиомы стереометрии состоят из аксиом планиметрии с уточнением «на» или «в заданной плоскости» и 3-х дополнительных аксиом.

2. Группа дополнительных аксиом стереометрии

1. Для любой плоскости в пространстве, существуют точки принадлежащие данной плоскости и точки не принадлежащие ей.

2. Две различные плоскости, имеющие одну общую точку, пересекаются по прямой, проходящей через эту точку.

3. Через две различные прямые, имеющие общую точку, можно провести только одну плоскость.

Рис. 1. Аксиомы стереометрии.

Пример

Даны три попарно пересекающиеся плоскости. Две прямые пересечения из них пересекаются. Доказать, что три прямые пересечения этих плоскостей пересекаются в одной точке.

Пусть даны три попарно пересекающиеся плоскости α, β и γ. Плоскость α пересекает плоскость β по прямой а. А плоскость β пересекает плоскость γ по прямой с (Рис. 2 а).

точка Е ∈ а,с (прямые пересекаются в точке Е по условию задачи)

Тогда плоскости α и γ пересекаются по прямой b.

Отсюда следует, что, т.к. прямые b,с ∈ γ, то они либо параллельны, либо пересекаются в какой-то точке Е₁.

Если они параллельны, то у них нет общих точек, а следовательно, плоскости α и β пересекаются по прямой а, параллельной b и с (Рис. 2 б). А это противоречит условию задачи. Следовательно, прямые b и с пересекаются в какой-то точке Е₁.

Отсюда можно сделать вывод, что точка Е₁ принадлежит трем плоскостям α,β,γ и, следовательно, она лежит одновременно на трех прямых а, b и с. А это возможно только, если три прямые пересекаются в одной точке. И, следовательно, прямая b пересекает прямую с в точке Е₁, которая является точкой пересечения прямых а и с. Таким образом, точки Е и Е₁ совпадают.

Рис.2. Даны три попарно пересекающиеся плоскости.

3. Плоскость, проходящая через данную прямую и точку

Теорема: Через прямую и не лежащую на ней точку можно провести только одну плоскость.

Доказательство.

Пусть АВ данная прямая и Е не принадлежащая ей точка. (Рис.3) Проведем через точки А и Е прямую. Тогда прямые АВ и АЕ пересекаются в точке А. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость α, проведенная через эти прямые, единственная. Т.к. точка Е принадлежит прямой АЕ, то она принадлежит плоскости α.

Если допустить, что существует еще одна плоскость α’, проходящая через прямую АВ и точку Е, то эта плоскость пересекает плоскость α по прямой, на которой лежат точки А, В, и Е согласно аксиоме 2. А это противоречит условию, т.к. точки А, В, и Е не лежат на одной прямой. Следовательно, плоскость α единственная.

Рис. 3 Плоскость, проходящая через данную прямую и точку.

4. Пересечение прямой с плоскостью

Теорема: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит данной плоскости.

Доказательство.

Проведем через прямую а и точку С плоскость β. Тогда, если плоскости α и β совпадают, то прямая а принадлежит плоскости α, что и утверждает данная теорема. Если плоскости α и β не совпадают, то они пересекаются по прямой а’. Таким образом, имеем:

точки А и В ∈ а, α
прямая а ∈ β
следовательно, точки А и В ∈β

Отсюда следует, что две точки А и В принадлежат двум плоскостям: α и β. И, согласно аксиоме, они могут лежать только на прямой а’, которая является прямой пересечения этих плоскостей. Т.к. через две точки можно провести только одну прямую, и по условию теоремы эта прямая есть а, то следовательно, она и является прямой пересечения двух плоскостей. Т.е. прямые а и а’ совпадают. А следовательно, прямая а принадлежит плоскости α.

Из данной теоремы следует, что плоскость и не принадлежащая ей прямая, либо не пересекаются, либо пересекаются в одной точке.

Рис. 4 Пересечение прямой с плоскостью.

5. Существование плоскости, проходящей через три данные точки

Теорема. Через три точки, не лежащие на данной прямой, можно провести только одну плоскость. Рис.5

Доказательство. Пусть А, В, С три точки, не лежащие на одной прямой. Проведем через точки А,С и В,С прямые. Тогда они пересекаются в точке С. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость, проведенная через эти прямые, единственная. По теореме о пересечении прямой с плоскостью, обе прямые целиком принадлежат данной плоскости.

Рис. 5 Существование плоскости, проходящей через три данные точки.

6.Пример 1

Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Доказательство:

Пусть дана данная прямая а и точка О, не принадлежащая прямой а. И даны пересекающие ее прямые b, c, d в точках B, C, D, которые пересекаются в точке О. Проведем через прямую а и точку О плоскость α (Рис.6).

По теореме о пересечении прямой и плоскости, если провести прямую b, проходящую через точку О и точку В прямой а, то она целиком будет принадлежать плоскости α, так как две точки прямой b принадлежат плоскости α.

Если допустить, что прямая b не принадлежит плоскости α, то в этом случае мы можем провести плоскость α’, проходящую через точки В и О. Тогда плоскости α и α’ пересекаются по прямой b’, проходящей через точки В и О. А так как через две точки можно провести только одну прямую, то прямые b и b’ совпадают. Следовательно, прямая b целиком принадлежит плоскости α.

Точно так же доказывается, что прямые с и d принадлежат плоскости α. Отсюда можно сделать вывод, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Рис.6 Задача. Докажите, что все прямые, пересекающие данную прямую.

Пример 2

Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую.

Доказательство:

Пусть даны две непересекающиеся плоскости α и α’. И прямая а, которая пересекает плоскость α в точке В (Рис.7). Необходимо доказать, что прямая а пересекает плоскость α’ в точке В’.

Возьмем на плоскости α’ точку А и проведем через нее и прямую а плоскость β. Тогда плоскость β будет пересекать плоскости α и α’ по параллельным прямым b и b’. Точка В принадлежит прямой b, так как она принадлежит плоскости α и лежит на прямой а. И следовательно, она принадлежит двум плоскостям α и β.

Таким образом получается, что на плоскости β лежат две параллельные прямые b и b’. Одну из них пересекает прямая а в точке В. Следовательно, прямая а пересекает и вторую прямую b’. Так как согласно аксеоме, через точку В, не лежащей на данной прямой b’, можно провести только одну, параллельную прямой b’, прямую b. Отсюда следует, что прямая а не параллельна прямой b’, она ее пересекает в точке B’.

Рис.7 Задача. Даны две непересекающиеся плоскости.

Пример 3

Даны две плоскости, пересекающиеся по прямой а. И прямая b, которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые а и b пересекаются.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Прямая b лежит в плоскости β и пересекает плоскость α в точке А (Рис.8). Необходимо доказать, что прямая b пересекает прямую а.

По условию задачи, прямая b лежит в плоскости β и пересекает плоскость α в точке А. Следовательно, точка А принадлежит двум плоскостям α и β.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что, так как точка А принадлежит двум плоскостям, то она лежит на прямой а, потому что прямая а является прямой пересечения двух плоскостей α и β.

Таким образом, точка А принадлежит двум прямым а и b. А следовательно, эти прямые пересекаются.

Рис.8 Задача. Даны две плоскости, пересекающиеся по прямой а.

Пример 4

Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Точки А, В, С одновременно принадлежат двум плоскостям α и β (Рис.9). Необходимо доказать, что все три точки принадлежат прямой а.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что все три точки А, В и С лежат на прямой пересечения двух плоскостей, т.е. прямой а, так как они принадлежат обоим плоскостям α и β.

Пусть дана точка D, принадлежащая только плоскости β. Тогда она не может лежать на прямой а, так как она не принадлежит плоскости α. Точно так же точка Е не может принадлежать прямой а, так как она принадлежит только плоскости α. Точка F не принадлежит плоскостям α и β, а следовательно, и прямой а.

Рис.9 Задача. Точки А, В, С лежат в каждой из двух различных плоскостей.

Пример 5

Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки. Докажите, что данные четыре точки не лежат в одной плоскости.

Доказательство:

Пусть даны четыре точки А, В, С, D. Допустим, что все четыре точки лежат в одной плоскости α.

Прямая АВ не пересекается с прямой CD. Прямая АС также не пересекается с прямой BD. Если провести прямую AD, то точки В и С окажутся в разных полуплоскостях. Следовательно, прямая AD пересекается с прямой ВС в точке О (Рис.10 а).

Допустим, что прямая AB не пересекает прямую DС (Рис.10 б). АD не пересекает прямую BC. Тогда, если провести прямую АС, то точки B и D окажутся в разных полуплоскостях. И прямая АС будет пересекать прямую BD в точке О.

Теперь допустим, что прямая AC не пересекает прямую ВD (Рис.10 в). АD не пересекает прямую ВC. Тогда, если провести прямую АВ, то точки D и C окажутся в разны полуплоскостях. А следовательно, прямая АВ будет пересекать прямую СD в точке О.

Отсюда можно сделать вывод, для того, чтобы выполнялось условие, при котором прямые АВ, АС, АD, одновременно не пересекали бы прямые CD, BD, BC, необходимо чтобы четыре точки А, В, С и D лежали в разных плоскостях.

Рис.10 Задача. Даны четыре точки. Известно, что прямая.

Источник

• Популярная книга Круть доступна для чтения прямо сейчас на нашем сайте boochi.ru. Скачать книгу в формате FB2, TXT, PDF, EPUB бесплатно без регистрации. →

Главная > Учебные материалы > Математика: Стереометрия. Страница 1