Докажите что через две произвольные точки можно провести хотя бы одну плоскость

Докажите, что через любые две точки можно провести хотя бы одну плоскость?

Докажите, что через любые две точки можно провести хотя бы одну плоскость.

Через любые две точки можно провести единственную прямую.

А через прямую можно провести бесконечно много плоскостей.

Периметр треугольника равен 24, докажите что расстояние от любой точки плоскости, до хотя бы одной из его вершин больше 4?

Периметр треугольника равен 24, докажите что расстояние от любой точки плоскости, до хотя бы одной из его вершин больше 4.

Укажите в ответе номера верных утверждений?

Укажите в ответе номера верных утверждений.

Через любую точку плоскости можно провести прямую?

Через любую точку плоскости можно провести прямую.

Докажите, что через прямую можно провести две различные плоскости?

Докажите, что через прямую можно провести две различные плоскости.

6. Четыре точки не лежат в одной плоскости?

6. Четыре точки не лежат в одной плоскости.

7. Докажите, что через прямую можно провести две различные плоскости.

Через любую точку плоскости можно провести прямую?

Через любую точку плоскости можно провести прямую.

Верно или не верно?

Верно или не верно.

1. Через любую точку плоскости можно провести прям?

2. Через любые две различные точки плоскости можно провести прямую?

3. Через любые три различные точки плоскости можно провести прямую?

4. Любые две различные прямые проходят через одну общую точку?

Докажите что любые прямые пересекающие эти прямые и не проходящие через точку М, лежат в одной плоскости.

Докажите что через любые 2 точки можно провести плоскость?

Докажите что через любые 2 точки можно провести плоскость.

Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и притом одну?

Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и притом одну.

1)УголCAD = 150 2)AD = 15см 4)MD = 2см.

УголM = P = 60 ГРАДУСОВ уголN = L = 135 ГРАДУСОВ.

Подобие треугольников. Ладно, легче пересканировать.

Источник

Докажите что через две точки можно провести две различные плоскости сколько существует таких плоскостей?

Докажите что через две точки можно провести две различные плоскости сколько существует таких плоскостей.

Пусть даны точки А и В.

Возьмем третью точку С отличную от А и В.

Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

Проведем плоскость АВС

Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

Возьмем точку D не принадлежщую плоскости АВС (таковая существует за аксиомой выше)

Проведем плоскость АВD.

Эти плоскости разные так как точка D не принадлежит плоскости АВС.

И данные точки А и В принадлежат одновременно и плоскости АВС и ABD.

Таким образом существование искомых плоскостей доказано

Дана плоскость а и точка А вне нее?

Дана плоскость а и точка А вне нее.

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости.

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости?

Варианты ответов : Две Три Одну Бесконечно.

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости?

Сколько прямых можно одновременно провести через две точки на плоскости?

Через A B иC можно провести две различные плоскости?

Через A B иC можно провести две различные плоскости.

Каково взаимное расположение точек?

Выберите верные утверждения?

Выберите верные утверждения.

1) Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

2) Если две прямые в пространстве перпендикулярны, то они пересекаются.

3) Через точку и прямую всегда можно провести плоскость.

4) Если две различные прямые перпендикулярны одной плоскости, то они перпендикулярны.

Изобразить три точки на плоскости так, чтобы через каждые две из них можно было провести прямую?

Изобразить три точки на плоскости так, чтобы через каждые две из них можно было провести прямую.

Сколько получится разных прямых?

Сколько плоскостей можно провести через две точки пространства?

Сколько плоскостей можно провести через две точки пространства?

Ни одной Одну Две Бесконечно много Напишите верный ответ.

Источник

Докажите что через две произвольные точки можно провести хотя бы одну плоскость

Различные подходы к определению проективной плоскости

Исторический обзор аксиоматического построения проективной геометрии

Глава 1. Определение проективной плоскости на базе трехмерного

Глава 2. Аналитическое построение проективной плоскости.

2.1. Понятие проективной плоскости.

2.2. Свойства проективной плоскости.

2.3. Теорема Дезарга.

Глава 3. Аксиоматическое построение проективной плоскости.

3.1. Аксиоматика аффинной плоскости.

3.2. Аксиоматика проективной плоскости.

3.3. Модели проективной плоскости.

3.4. Теорема Дезарга.

3.5. Принцип двойственности.

3.6. Гармоническая четверка точек.

3.7. Перспективные и проективные отображения.

3.8. Аксиома Паппа и основная теорема о проективных преобразованиях прямой.

Глава 4. Применение основных теорем к решению задач на евклидовой плоскости.

4.1. Использование теоремы Дезарга на евклидовой плоскости.

4.2. Использование предложения Паппа на евклидовой плоскости.

Понятие проективной плоскости можно ввести многими способами. Проективную плоскость можно построить на базе трехмерного векторного пространства, аналитически и аксиоматически.

В данной работе, в ее первой главе, проективная плоскость Р2 строится на базе трехмерного векторного пространства, рассматриваются свойства проективной плоскости и ее модели. В конце главы доказываются теоремы: Дезарга и Паппа.

Во второй главе проективная плоскость рассматривается как множество проективных точек, каждая из которых представляет собой класс пропорциональных троек действительных чисел, не содержащей нулевой тройки. При данном подходе к построению проективной плоскости рассматриваются свойства, доказывается теорема Дезарга.

В третьей главе уделяется внимание построению проективной плоскости аксиоматически. Прежде чем определить проективную плоскость, вводится аксиоматика аффинной плоскости. После определения проективной плоскости рассматриваются 4 ее модели. Особое внимание уделяется теореме Дезарга. На основе изложенного в третьей главе материала делается вывод о двойственности на проективной плоскости. В этой главе также определяются понятия: гармоническая четверка точек, перспективные и проективные отображения. Завершает главу аксиома Паппа и основная теорема о проективных преобразованиях прямой.

Глава четвертая изучает использование теорем Дезарга и Паппа на евклидовой плоскости. После чего приводятся решения задач, при решении которых использовались доказанные выше теоремы.

Вся история геометрии дает поучительный пример того, как эта наука материальные корни которой берут свое начало из жизненных потребностей человеческого общества (землемерие, постройка жилищ, живопись), достигла высокого теоретического уровня, выработала свои специфические и вместе с тем весьма общие методы, которые в свою очередь сделали возможным новые плодотворные применения геометрии к практическим вопросам.

Исторический обзор аксиоматического построения проективной геометрии.

Имеются различные аксиоматические способы построения проективного пространства. Наиболее распространенным является видоизменение системы аксиом, предложенной в 1899 году Гильбертом для обоснования элементарной геометрии.

Проективное пространство рассматривается как совокупность элементов трех родов: точек, прямых и плоскостей, между которыми установлено основное для проективной геометрии отношение инцидентности, характеризующееся надлежащими аксиомами. Они отличаются от соответствующих групп аксиом элементарной геометрии, тем, что требуют, чтобы каждые две прямые, лежащие в одной плоскости, имели общую точку и на каждой прямой имелось, по крайней мере, три различные точки. В конкретных случаях для получения более “богатой” проективной геометрии эта совокупность аксиом дополняется аксиомами порядка и непрерывности (для действительного проективного пространства), аксиома Паппа (для проективной геометрии над коммутативными телами), Фано постулатом (для проективной геометрии над телами, характеристика которого порядка ¹ 2) и т.д.

Замечательным положением проективной геометрии является принцип двойственности. Говорят, что точка и прямая (точка и плоскость, прямая и плоскость) инцидентны, если точка лежит на прямой (или прямая проходит через точку и т.д.). Тогда если верно некоторое предположение А о точках, прямых и плоскостях проективного пространства, сформулированные только в терминах инцидентности между ними, то будет верно и двойственное предложение В, которое получается из А заменой слова “точка” на слово “плоскость”, слово “плоскость” на слово “точка” и с сохранением слова прямая.

Важную роль в проективной геометрии играет Дезарга предложение, выполнение которого необходимо и достаточно для введения проективными средствами системы проективных координат, составленных их элементов некоторого тела К, естественным образом связанного с точкой проективной прямой.

Основы проективной геометрии заложены в 17в Ж. Дезаргом и Б. Паскалем. Большое значение для последующего развития проективной геометрии имели работы П. Монтена (2-я полов. 18в – нач. 19в).

Как самостоятельная дисциплина проективная геометрия была изложена Понселе (нач. 19в). Заслуга Ж. Понселе заключается в выделении проективных свойств фигур в отдельный класс, и установлении соответствий между метрическими и проективными свойствами этих фигур.

К этому же периоду относятся работы Ж. Брионшона. Дальнейшее развитие проективная геометрия получила в трудах Я. Штейнера и М. Шаля. Большую роль в развитии проективной геометрии сыграли работы К. Штаудта, в которых были намечены также контуры аксиоматического построения проективной геометрии.

Все эти геометрии, стремились доказать теоремы проективной геометрии синтетическим методом, положив в основу изложенные проективные свойства фигур.

Аналитическое направление в проективной геометрии было намечено работами А. Мебиуса. Влияние на развитие проективной геометрии оказали работы Н.И. Лобачевского по созданию неевклидовой геометрии, позволившие в дальнейшем А. Кэли и Ф. Клейну рассмотреть различные геометрии, систематизировать с точки зрения проективной геометрии.

Развитие аналитических методов обычной проективной геометрии и построение на этой базе комплексной проективной геометрии поставили задачу о зависимости тех или иных проективных свойств от того тела, над которым построена геометрия. В решении этого вопроса больших успехов добились А.Н. Колмогоров и Л.С. Понтрягин.

Глава 1. Определение проективной плоскости на базе трехмерного векторного пространства.

Рассмотрим определение проективной плоскости Р2. Понятие проективной плоскости строится на базе трехмерного векторного пространства V3.

Определение: Не пустое множество Р2 называется проективным плоскостью, если существует отображение j множества ненулевых векторов V3 в Р2 удовлетворяющее двум условиям:

j (х)= j (у) Û х,у – линейно зависимы.

1.2. Свойства проективной плоскости.

Рассмотрим свойства проективной плоскости Р2.

Доказательство : Рассмотрим проективную плоскость Р2 построенную на базе V3.

Пусть точка А порождена вектором а Î V3 ( т.е. j (а)=А).

() В порождена b Î V3(т.е. j ( b )=В);

V1( а )=A V1 Ì V2 Þ A Î l

V1( b )= B V1′ Ì V2 Þ B Î l

Р2 построено на базе V3

1) V2 ¹ V2′, так как l ¹ m

так как V1 Ì V2 Þ A Î l

l и m пересекаются в единственной ()А.

Покажем, что эти точки не лежат на одной прямой. Если бы эти точки принадлежали одной прямой, то вектора порождающие их должны были принадлежать V2, чего быть не может, так как эти вектора линейно независимы.

Вывод: На каждой прямой лежит не менее трех точек.

Замечание : Любая четверка точек проективной плоскости линейно зависима.

1.3. Модели проективной плоскости.

Связкой прямых в Е3 называется множество прямых пространства проходящих через некоторую фиксированную ().

Источник

Содержание:

Стереометрия:

Что такое стереометрия

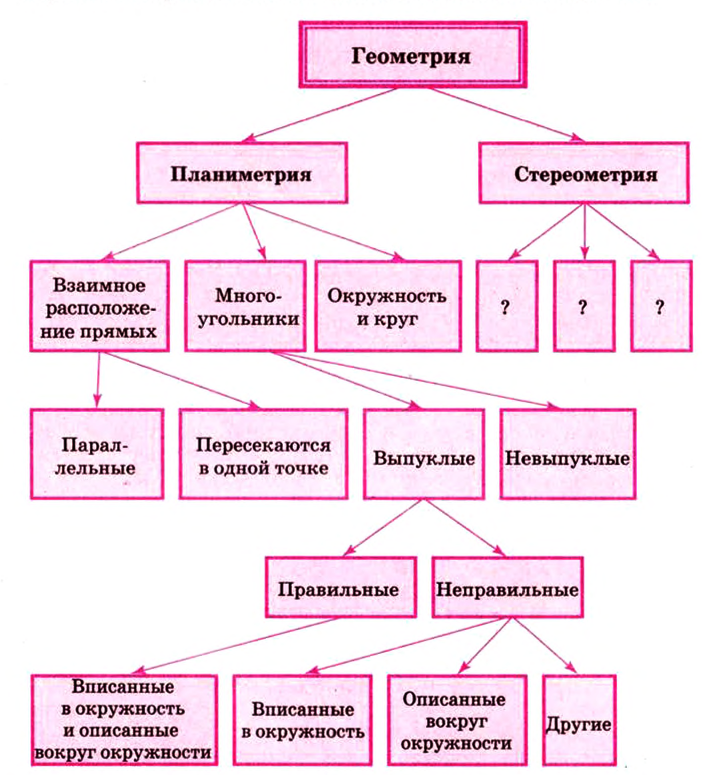
Схематически это выглядит так:

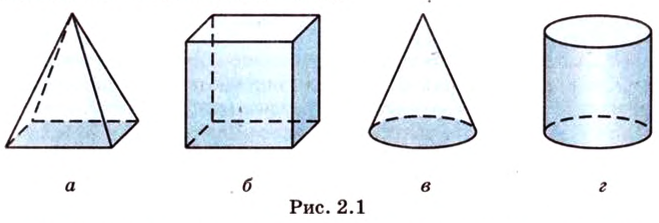
Фигуры, которые изучаются в стереометрии, называются геометрическими или пространственными. На рисунке 2.1 изображены некоторые пространственные фигуры: пирамида, параллелепипед, конус, цилиндр.

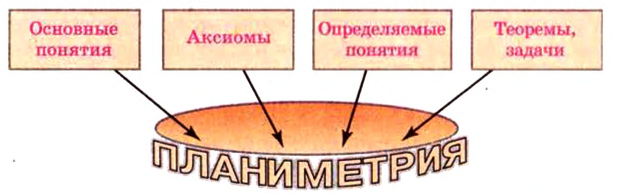
Напомним структуру логического построения планиметрии:

В стереометрии рассматривают более одной плоскости. Пространство состоит из бесконечного количества плоскостей, прямых и точек. Поэтому все аксиомы планиметрии имеют место и в стереометрии. Однако при этом некоторые из них приобретают другой смысл. Так, аксиома I, в планиметрии утверждает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Именно в таком понимании эта аксиома применялась в процессе построения геометрии на плоскости. Теперь эта аксиома утверждает вообще существование точек, не лежащих на данной прямой, в пространстве. Из нее непосредственно не вытекает, что существуют точки вне данной прямой на плоскости, в которой лежит прямая. Это требует уже специального доказательства.

Аксиомы стереометрии

Формулирование некоторых аксиом планиметрии как аксиом стереометрии требует уточнения. Это касается, например, аксиом .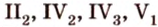

Приведем эти уточнения.

Понятно, что с увеличением количества основных фигур появляются новые аксиомы об их свойствах:

Аксиома 1 указывает на то, что любая плоскость все пространство не исчерпывает. Существуют точки пространства, которые ей не принадлежат.

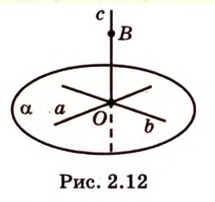
Аксиома 2 утверждает, что две прямые, пересекающиеся в пространстве, всегда определяют одну плоскость. Из аксиомы 3 следует, что если две различные плоскости имеют общую точку, то они имеют множество общих точек, образующих прямую, которая содержит эту точку.

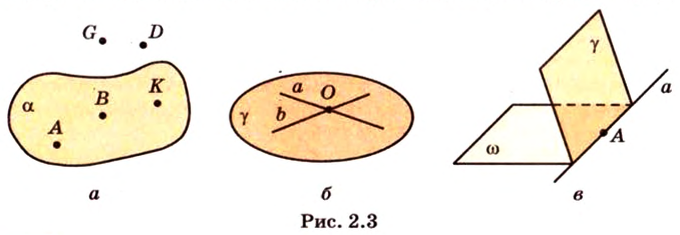
Итак, используя рисунок 2.3, аксиомы можно записать:

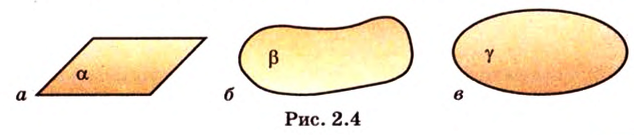
Плоскости изображают по-разному. На рисунке 2.4 показаны некоторые примеры различных изображений плоскостей.

Далее в стереометрии мы будем использовать все определяемые понятия планиметрии, дополнять их новыми, собственно стереометрическими, формулировать и доказывать свойства пространственных фигур.
Как видим, логическое построение планиметрии и стереометрии одинаково, отличаются они лишь некоторым содержанием основных понятий, аксиом, определений, теорем.

Пример №1

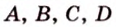
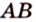
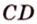
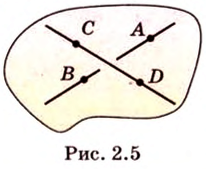
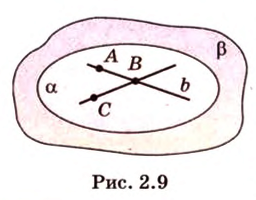
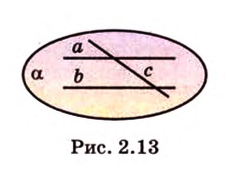
Точки не лежат на одной плоскости. Докажите, что прямые и не пересекаются.

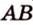
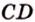
Докажем методом от противного. Допустим, что прямые и пересекаются (рис. 2.5).

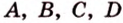
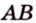
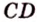
Тогда, по аксиоме II₃, через них можно провести плоскость, которой принадлежат эти прямые. Это означает, что точки также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые и не пересекаются, что и требовалось доказать.
Заметим, что школьный курс геометрии посвящен евклидовой геометрии. Несмотря на то что с течением времени геометрия Евклида была существенно дополнена и откорректирована, ее по-прежнему называют именем древнего ученого. Такое уважение вызвано широтой практического применения евклидовой геометрии. Она используется в технических науках, картографии, геодезии, астрономии и др.

Следствия из аксиом стереометрии

Проанализировав все сказанное ранее, можно утверждать, что логическое построение геометрии имеет следующий вид:

Важное место в геометрии занимают аксиомы. Они выражают наиболее существенные свойства основных геометрических фигур. Все остальные свойства геометрических фигур устанавливаются рассуждениями, опирающимися на аксиомы или ранее доказанные утверждения, которые опираются на аксиомы. Такие рассуждения называют доказательствами. Утверждение, истинность которого доказана и которое используют для доказательства других утверждений, называют теоремой. Простейшими из них являются утверждения для основных фигур стереометрии. Они называются следствиями из аксиом стереометрии. Рассмотрим теоремы, которые являются следствиями из аксиом стереометрии.

Теорема 1

Через прямую и точку, не принадлежащую ей, можно провести плоскость, и притом только одну.

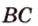
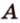
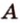
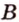
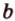
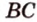
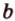
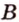
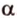
Пусть — данная прямая и — точка, не принадлежащая ей (рис. 2.9). Через точки и проведем прямую . Прямые и различны и пересекаются в точке . По аксиоме II₃ через них можно провести плоскость . Докажем, что она единственная, методом от противного.

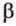
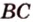
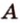
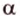
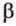
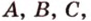
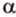
Допустим, что существует другая плоскость , которая содержит прямую и точку . Тогда, согласно аксиоме II4, плоскости и пересекаются по общей прямой, которой принадлежат точки что противоречит условию. Предположение неверно. Плоскость — единственная. Теорема доказана.

Теорема 2
Если две точки прямой принадлежат плоскости, то и вея прямая принадлежит этой плоскости.

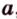
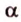
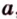
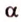
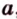
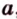
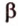
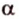
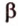
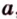
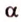
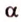
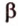
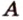
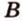
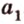
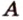
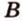
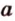
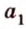
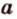
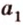
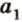
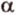
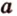
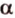
Пусть заданы прямая , плоскость и точки А и В прямой , принадлежащие (рис. 2.10). Выберем точку С, которая не принадлежит прямой . Через точку С и прямую проведем плоскость . Если и совпадут, то прямая принадлежит плоскости . Если же плоскости и различны и имеют две общие точки и , то они пересекаются по прямой , содержащей эти точки. Поэтому через две точки и проходят две прямые и , что противоречит аксиоме принадлежности I₂. Поэтому и — совпадают. Однако поскольку , принадлежит плоскости , то и прямая также принадлежит .

Теорема 3

Через три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

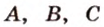
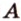
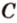
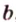
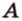
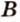
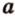
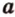
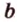
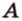
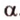
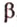
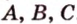
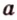
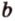
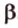
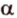
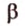
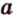
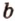
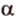
Пусть — заданные точки (рис. 2.11). Проведем через точки и прямую , а через точки и — прямую . Прямые и различны и имеют общую точку . Через них можно провести плоскость . Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость , содержащая точки . Тогда, по теореме 2, прямые и принадлежат плоскости . Поэтому плоскости и имеют две общие прямые и , которые пересекаются, что противоречит аксиоме II₃. Итак, плоскость — единственная. Теорема доказана.

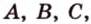
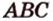
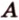
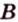
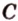
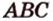
Отметим, если плоскость определена тремя точками, которые не лежат на одной прямой, например то в таком случае пользуются обозначением: (). Читается: «плоскость, заданная точками , и », или сокращенно «плоскость ».

Пример №2

Можно ли через точку пересечения двух данных прямых провести третью прямую, которая бы не лежала с ними в одной плоскости?

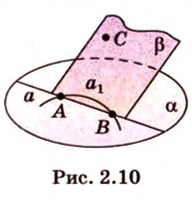
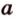
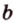
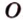
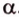
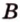
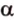
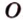
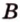
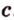
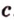
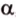
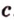
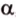
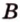
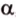
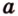
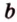
Через прямые и (рис. 2.12), которые имеют общую точку , можно провести плоскость . Возьмем точку , которая не принадлежит . Через точки и проведем прямую . Прямая не лежит на плоскости , так как если бы прямая принадлежала плоскости , то и точка принадлежала бы плоскости . Поэтому через точку пересечения прямых и можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.

Очевидно, что точки плоскости задают прямые, которые будут принадлежать этой самой плоскости. Если же взять точку пересечения двух прямых на плоскости и точку вне плоскости, то через любые две точки пространства можно провести прямую. Эта прямая будет иметь только одну общую точку с плоскостью, а значит, будет ее пересекать.

Пример №3

Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.

Пример №4

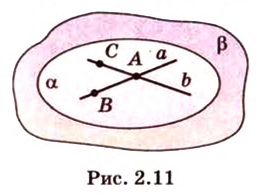
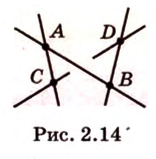
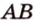
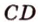
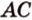
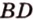
Докажите, что если прямые и не лежат в одной плоскости, то прямые и также не лежат в одной плоскости.

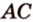
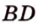
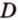
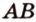
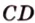
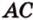
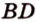
Докажем методом от противного. Допустим, что прямые и лежат в одной плоскости (рис. 2.14). Тогда точки принадлежат этой плоскости, а следовательно, прямые и принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые и не принадлежат одной плоскости, что и требовалось доказать.

Пример №5

Сколько всего существует различных плоскостей, проходящих через прямую и точку в пространстве?

Если в пространстве даны прямая и точка, лежащая на ней, то ими определяется множество плоскостей, поскольку через прямую проходит множество различных плоскостей.
Если же точка не лежит на прямой, то по следствию из аксиом стереометрии такую плоскость можно построить только одну.

Ответ. Бесконечно много или одна.

Взяв вне этой прямой произвольную точку, мы всякий раз будем иметь другую плоскость, не совпадающую с ранее построенной. Таких плоскостей множество.
Через данную точку вне прямой можно провести либо прямую, которая пересекает данную прямую, либо прямую, параллельную данной. Оба случая задают одну плоскость.

Сечения

Анализируя окружающий мир и систематизируя его предметы по форме, мы убеждаемся, что много из них «усечены» или «склеены». Разъединив их, получим поверхность, которую называют их сечением.

С сечениями мы сталкиваемся в разнообразных ситуациях: в быту, в столярничестве, токарстве и т.д. Решением задач на сечения геометрических фигур или других тел занимаются в черчении и конструкторской практике. Сечения выполняют для пространственных геометрических фигур.

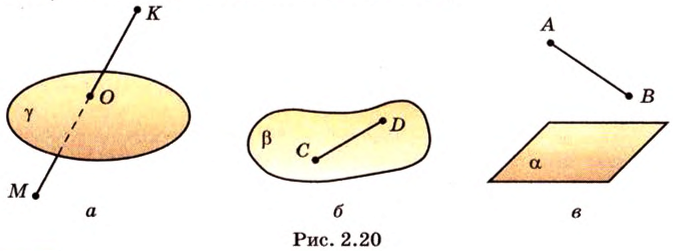
Каждая плоскость разбивает пространство на два полупространства, а концы отрезка могут лежать в различных полупространствах (рис. 2.20, а) относительно некоторой плоскости, на плоскости (рис. 2.20, б) или в одном полупространстве (рис. 2.20, в).

Если ни одна из двух точек не принадлежит плоскости, а отрезок, соединяющий их, имеет с этой плоскостью общую точку, то говорят, что данные точки лежат по разные стороны относительно плоскости, или отрезок пересекает плоскость. Если же как минимум две точки пространственной геометрической фигуры лежат по разные стороны плоскости, то говорят, что плоскость эту фигуру пересекает, такую плоскость называют секущей.

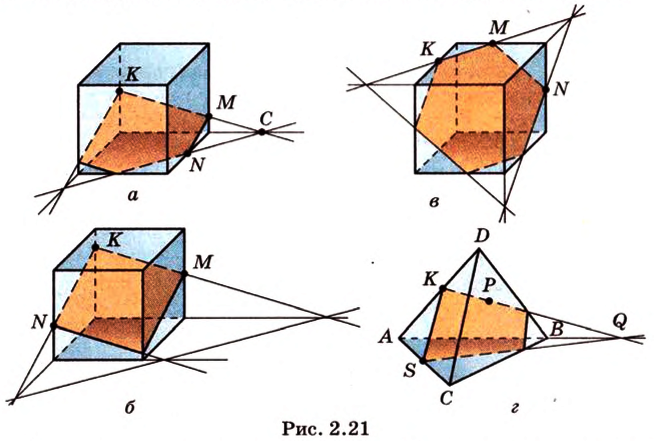
Фигура, которая состоит из всех общих точек геометрической фигуры и секущей плоскости, называется сечением геометрической фигуры. На рисунке 2.21 сечения изображены цветом.

Если плоскость грани многогранника и плоскость сечения имеют две общие точки, то они пересекаются по прямой, проходящей через эти точки. Эту прямую называют линией пересечения данных плоскостей.
Плоскость сечения многогранника имеет общие прямые с плоскостями граней многогранника. Прямую, по которой плоскость сечения пересекает плоскость любой грани многогранника, называют следом плоскости сечения. Следов столько, сколько плоскостей граней пересекает плоскость сечения.

При построении сечения следует помнить:

Рассмотрим примеры построения сечения многогранника секущей плоскостью.

Пример №6

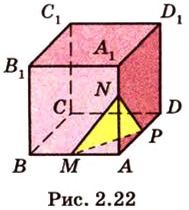
Постройте сечение куба плоскостью, проходящей через середины ребер с общей вершиной.

Построение

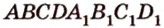
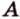
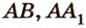
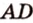
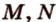
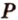
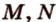
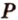
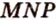
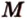
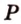
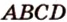
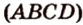
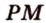
Пусть — заданный куб (рис. 2.22). Выберем одну из вершин, например , являющуюся общей для трех ребер и . Обозначим на этих ребрах точки и соответственно, являющиеся их серединами. Точки и не лежат на одной прямой, а поэтому определяют секущую плоскость (). Точки и — общие точки плоскости сечения и грани , поэтому , — сторона сечения.
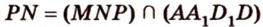
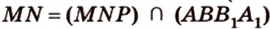
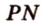
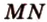
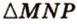
Аналогично и , поэтому и — две другие стороны сечения. Таким образом, — искомое сечение.

Пример №7

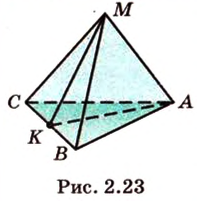
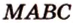
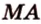
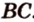
Постройте сечение пирамиды плоскостью, которая проходит через ребро и середину ребра .

Построение

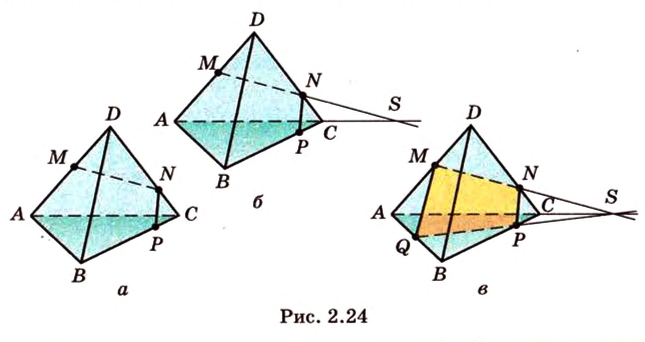
Пример №8

Постройте сечение пирамиды плоскостью, проходящей через три точки, которые лежат соответственно на ребрах , .

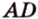
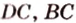
Построение

Рассмотрим случай, когда ни одна из прямых, проходящих через эти точки, не будет параллельна сторонам граней.

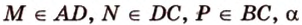
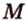
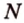
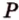
Пусть — секущая плоскость, проходящая через заданные точки , и . Построим сечение, выполняя последовательно шаги:

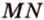
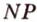
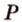
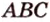
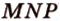
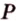
Мы нашли две стороны фигуры сечения: отрезки и (рис. 2.24, а). Точка — общая точка двух плоскостей () и (). Такие плоскости (по аксиоме II₄) пересекаются по прямой, проходящей через точку . Для построения такой прямой нужна вторая точка.

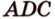
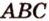
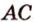
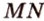
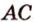
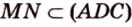
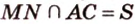
3. Плоскости () и () пересекаются по прямой . по условию не параллельна и , поэтому (рис. 2.24, б).
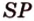
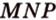
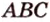
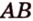
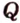
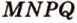
4. Прямая — линия пересечения плоскостей () и (). Пересечение этой прямой с ребром дает точку , которая является вершиной сечения. Таким образом, четырехугольник — искомое сечение (рис. 2.24, в).

Пример №9

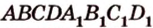
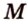
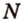
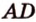
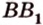
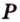
Постройте сечение прямоугольного параллелепипеда плоскостью, проходящей через середины и ребер и и точку пересечения диагоналей грани (рис. 2.25, а).

Построение

Обозначим секущую плоскость 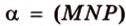. Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.

Таким образом, пятиугольник 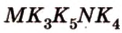— искомое сечение (рис. 2.25, г).
Приведем краткие описания построения сечения куба плоскостью, проходящей через три точки.

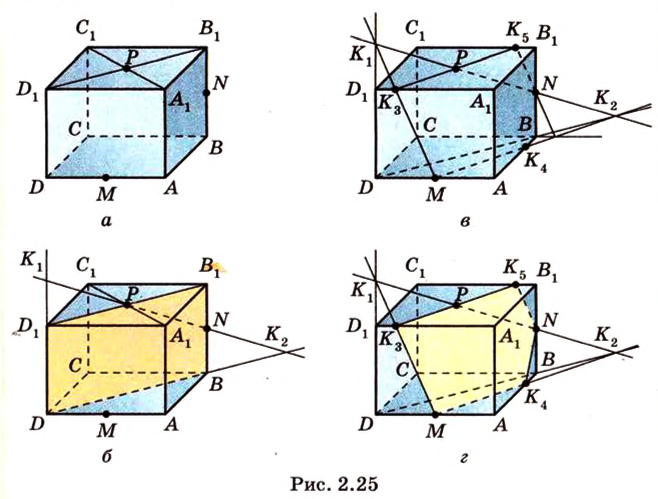
Пример №10

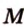
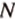
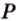
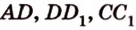
Постройте сечение куба плоскостью, проходящей через точки , , , которые принадлежат соответственно ребрам .

Построение

Секущая плоскость 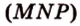) (рис. 2.26).

Пример №11

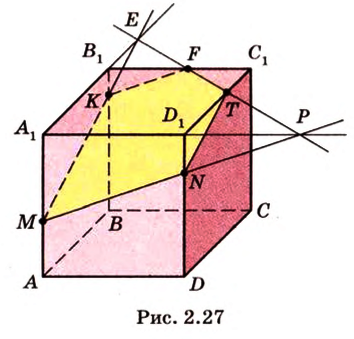
Постройте сечение куба плоскостью, проходящей через точки К, М, Т, которые принадлежат соответственно ребрам , .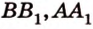

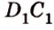
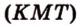
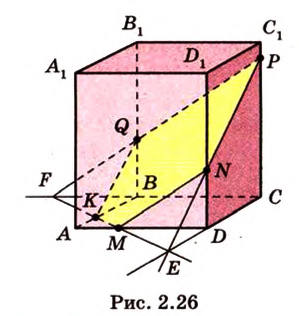
Секущая плоскость (рис. 2.27).

Пример №12

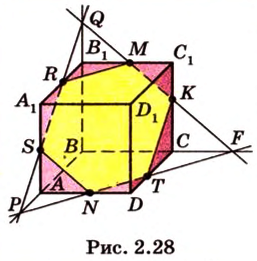
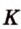
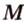
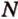
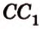
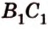
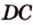
Постройте сечение куба плоскостью, проходящей через точки , , , которые принадлежат соответственно ребрам ,, .

Построение

Секущая плоскость 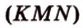(рис. 2.28).

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник