Докажите что если для положительной бесконечной десятичной дроби все приближения по недостатку

1.2. Десятичные дроби и действительные числа

Дроби, у которых знаменатель представляет собой степень десятки, т. е. 10, 102 = 100, 103 = 1000 и т. д., называются Десятичными дробями. Записываются они особым образом:

Попытка записать любую обыкновенную дробь в виде де­сятичной дроби приводит иногда к Бесконечной десятич­ной дроби. Например, разделив «уголком», мы получим:

Как видно, получающаяся бесконечная последователь­ность цифр содержит так называемый Период — один и тот же повторяющийся набор цифр. Поэтому получен­ные десятичные дроби называют Бесконечными перио­дическими десятичными дробями. Можно доказать, что любая обыкновенная дробь записывается в виде беско­нечной периодической десятичной дроби. Обратное так­же верно: любая бесконечная периодическая десятичная дробь представляет собой десятичную запись некоторой обыкновенной дроби. Как найти последнюю, поясним на примере.

Пример. Превратим в обыкновенные дроби числа Q = 0,777. и Р = 0,999.

Умножив на 10, получаем:

1) 10Q = 7,777. = 7 + Q, откуда 9Q = 7 и Q = .

Проверьте результат, превратив 7/9 в десятичную дробь.

2) 10P = 9,999. = 9 + р, откуда 9Р = 9 и Р = 1. Заме­тим, что 1 можно записать в виде бесконечной десятич­ной дроби с периодом 0: 1,000. ; аналогично, 0,24 = 0,24000. 3,5 = 3,5000. и т. п.

8. С помощью калькулятора и «вручную» превратите данную обыкновенную дробь в бесконечную периодическую десятичную дробь и укажите период: , , , , .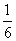

9. Превратите бесконечную периодическую десятич­ную дробь в обыкновенную: 1,888. ; 0,1212. ; 0,444.

Решив эти примеры, каждый будущий юрист задаст себе вопрос: а имеют ли смысл бесконечные Непериоди­ческие десятичные дроби?

Рассмотрим равнобедренный прямоугольный треуголь­ник, длина катетов которого равна единице. Обозначим длину гипотенузы через Х. По теореме Пифагора

. (1)

Докажем, что корни этого уравнения не являются рациональными числами. В самом деле, предположим противное, т. е. что корнем уравнения (1) является дробь (А и B — целые числа). Если дробь можно сократить, сделаем это, и будем полагать далее, что дробь является уже несократимой.

Подставляя в уравнение (1), получим = 2 или

. (2)

Так как в правую часть равенства (2) входит множитель 2, то А2 — число четное. Следовательно, число А также четное и его можно записать в виде А = 2С. Подставив в (2), получим (2С)2 = 2B2 или, сократив на 2, 2С2 = B2. Отсюда следует, что число B2 также является четным. Но тогда четным будет и число B. Теперь, поскольку оба числа А и B получились четными, дробь является сократимой. Это противоречит сделанному выше предпо­ложению, что дробь — несократимая. Противоречие возникло вследствие того, что в самом начале было сде­лано неверное предположение — корнем уравнения (1) является рациональное число — дробь . Следовательно, никакая дробь не может быть корнем уравнения (1), что и требовалось доказать.

Результат наших рассуждений можно сформулиро­вать иначе: квадратный корень из числа 2 не является рациональным числом, т. е. бесконечной периодической десятичной дробью.

Будем искать приближенные значения числа Х = 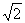. Ясно, что 1 2 = Х2, то 1,4 2. Следовательно, с точнос­тью до 0,01 получаем Х » 1,41. Применив еще раз тот же прием, найдем, что 1,414 2,381529. т. к. на первых четырех пози­циях соответствующие цифры одинаковы, а 6 > 5. Опи­санное правило сравнения работает при одном (и един­ственном) соглашении: не рассматривать периодические дроби с периодом 9. При этом множество действительных чисел, образно говоря, не сузится, т. к. всякую беско­нечную периодическую дробь с периодом 9 можно заме­нить равной ей Конечной десятичной дробью, например:

0,999. = 1, 0,42999. = 0,43, 2,65999. = 2,66 и т. п. (см. пример на с. 15).

Напомним свойства операций сложения и умноже­ния действительных чисел:

Переместительность или коммутативность:

Сочетательность или ассоциативность (для сложе­ния):

Сочетательность или ассоциативность (для умножения):

Распределительность или дистрибутивность:

Числовые множества N, Z, Q, R являются примера­ми так называемых Числовых систем, которые имеют специальные названия. Например, говорят Кольцо целых чисел, поле рациональных чисел, поле действительных чисел. Эти термины мы обсуждаем в восьмой главе. Там мы покажем, в частности, что поле действительных чи­сел можно расширить и получить так называемые Комп­лексные числа.

ПРАВИЛО ОКРУГЛЕНИЯ ДЕСЯТИЧНЫХ ДРОБЕЙ

Поясним на примере. Следующие десятичные дроби мы округляем до сотых долей:

10. Вычислите с помощью калькулятора и округлите до тысячных:

, , , , , , , , , .

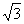
11. Найдите 3!, 4!, 5!, 6!, 7!, 81, 9!, 10!.

12. Расставьте правильно знаки > или 0, запишите ответ в виде бесконечной периодической десятичной дроби и округлите его до сотых.

ДЕЙСТВИЯ СО СТЕПЕНЯМИ

Из этого определения следует, что для любых натураль­ных чисел Т И п справедливы следующие формулы:

Am an = am+n, (an)m = amn, an bn = (Ab)N.

Число, которое при возведении в степень П дает A, на­зывается корнем степени N из А. Если число П нечетное, то существует только один корень степени П из числа А, Который обозначается или . Если N четное, а число А — положительное, то корней будет два. Напри­мер, числа 3 и –3 будут корнями четвертой степени из 81, т. к. 34 = 81 и (–3)4 = 81. Положительный корень на­зывается арифметическим и именно он обозначается символом или .

Степень с дробным показателем определяется так:

Оказывается, что имеют смысл и выражения вида Aх, Где Х — любое действительно число, например 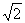. Дей­ствия с такими степенями производятся по тем же пра­вилам, что и с натуральными степенями, например, .

При различных вычислениях большие числа удобно записывать в так называемой Стандартной форме, т. е. в виде произведения двух множителей, первый из кото­рых заключен между числами 1 и 10, а второй пред­ставляет собой степень десятки: 243507 = 2,43507 • 105, 0,184 = 1,84 • 10–1 и т. д. Стандартную форму использу­ют при работе с калькулятором, в особенности тогда, когда не хватает разрядов для точных вычислений. На­пример,

243507 • 1385462 = 2,43507 • 105 • 1,385462 • 106 = (2,43507 • 1,385462) • 1011 » 3,37369695 • 1011;

317 = 316 • 3 = (34)4 • 3 = (81)4 • 3 = (6581)2 • 3 = 3 • (6,581 • 103)2 = 3 • (6,581)2 • (103)2 » 129,140163 • 106.

2. Вычислите, округляя в каждом действии резуль­тат до тысячных; окончательный результат округлите до сотых:

3. Найдите корни квадратного уравнения и округли­те результат до сотых:

Одна сотая доля какого-либо количества называется Процентом. Например, в городе N всего 300 судей, сле­довательно, 3 судьи — это 1%, 6 судей — 2% и т. д.

Подумайте, сколько тверских судей составляют 4% от их общего числа? (В Твери 145 судей.)

Другой пример. Некто утаил прибыль в размере 10 млн. руб. Какую сумму недополучила казна, если налог на прибыль составляет 22%?

Решение: 10 млн • = 2,2 млн.

4. За год в области совершено 6720 преступлений. Из них тяжких — 33; в состоянии алкогольного опьянения — 3262; связанных с дорожно-транспортными происшествиями — 1310. После завершения следствия переданы в суд 4520 дел; по 3816 из них уже вынесены приговоры, причем половина из последних — обвини­тельные; из всех обвинительных приведены в исполне­ние 40%. Заполните до конца следующую таблицу:

В первом столбце проставьте соответствующие абсолютные значения, а во втором укажите, какой процент они составляют от общего числа преступлений.

Источник

Докажите что если для положительной бесконечной десятичной дроби все приближения по недостатку

Докажите, что из 11 различных бесконечных десятичных дробей можно выбрать две такие, которые совпадают в бесконечном числе разрядов.

Подсказка

Для каждого разряда найдутся две дроби, совпадающие в этом разряде.

Решение

Выпишем 11 дробей друг под другом, чтобы цифры из одного разряда оказались в одном столбце. В каждом столбце 11 цифр, поэтому среди этих 11 цифр найдутся две равные. Пусть эти равные цифры находятся в k-й и m-й дробях. Поставим в соответствие этому столбцу пару чисел (k, m). Таким образом, каждому столбцу соответствует пара чисел от 1 до 11. Поскольку число пар таких чисел конечно, а число столбцов бесконечно, хотя бы одна из пар (k₀, m₀) была поставлена в соответствие бесконечному числу столбцов. Это означает, что дроби с номерами k₀, m₀ совпадают в бесконечном числе разрядов.

Источники и прецеденты использования

Источник

Приближение по недостатку и по избытку

Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.

Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.

Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.

Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.

Число π является бесконечной дробью 3,1415926535. Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.

Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.

Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.

Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.

Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213. то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.

Источник

Рациональные числа. Бесконечные числовые дроби

Логическая символика.

При изложении курса математического анализа для сокращения будем использовать логические символы ∀, ∃, ⇒ ⇔, значения которых приводятся ниже.

∀ — знак общности. Заменяет собой слова: для любого, для каждого, для всех.

∃ — знак существования. Заменяет собой слова: существует, найдется.

⇔ — знак равносильности (эквивалентности). Запись A ⇔ B означает, что B следует из A и A следует из B. Иначе: A равносильно B, A необходимо и достаточно для B; A тогда и только тогда, когда B.

Символы ∀, ∃ называются кванторами (общности и существования).

Кроме указанных символов, употребляются также следующие знаки:

∨ — знак дизъюнкции, заменяет союз «или»; запись A ∨ B означает, что имеет место хотя бы одно из высказываний A или B.

∧ — знак конъюнкции, заменяет союз «и».

⌉ — знак отрицания, запись ⌉A означает «не A» (отрицание высказывания А).

A = <квадратный трехчлен y = ax 2 + bx 2 + c принимает положительные значения при всех x>,

Пусть заданы числовое множество X и число M. Записать с помощью кванторов отрицание утверждений:

A = <все элементы x числового множества X удовлетворяют условию x 0 такое, что все элементы x из множества X удовлетворяют условию |x| ≥ M>.

Пусть A не имеет места, то есть не все элементы x множества X удовлетворяют условию x 0 такого, чтобы для любого x ∈ X имело место неравенство |x| ≥ M. Это означает, что для любого M > 0 неравенство |x| ≥ M не может выполняться для каждого x ∈ X. Иначе говоря, существует такой элемент x = x_M ∈ X (зависящий, вообще говоря, от M), для которого неравенство |x| ≥ M не выполняется, то есть справедливо неравенство |x| 0; \ \forall x \ \in \ X \ \rightarrow \ \left|x\right| \ \geq \ M\right\>\nonumber$$

$$\rceil B=\left\ <\forall M >0; \ \exists x_M \ \in \ X \ \rightarrow \ \left|x_M\right|

Рациональные числа и их свойства.

Рациональное число — такое число, которое можно записать в виде p/q, где p — целое число, q — натуральное число. В частности, любое целое число является рациональным, поскольку его можно записать в виде p = p/1. Например, 0 = 0/1, 1=1/1.

Пусть a = p/q, b = p₁/q₁ — два рациональных числа. Тогда правило упорядочения этих чисел определяется так:

Докажем, что решение данного уравнения \(\sqrt<3>\) не является рациональным числом.

Тогда p 2 можно записать так:

$$
p^2=p_0^<2x_0>\cdot p_1^<2x_1>\cdot\ldots\cdot p_n^<2x_n>\nonumber
$$
Поскольку p 2 делится на 3 целиком, то это значит, что в нашем разложении какое-то p_i = 3. А поскольку множество всех p_i (i лежит в пределах от 0 до n включительно) образует множество всех делителей исходного p, то 3 также является делителем p. То есть мы можем записать, что:
$$
p=3\cdot k,\qquad k\in\mathbb\nonumber
$$
То есть, если вернемся к одному из первых утверждений и заменим наше p, то получим:
$$
9\cdot k^2=3\cdot q^2\quad\Leftrightarrow\quad q^2=3\cdot k^2\nonumber
$$
Повторяя вышеизложенные рассуждения, получим, что q так же делится на 3, как и p. Предположим, что:
$$
q=3\cdot m,\qquad m\in\mathbb\nonumber
$$
Таким образом:
$$
\frac

=\frac<3\cdot k><3\cdot m>=\frac,\nonumber
$$
что противоречит первоначальному утверждению, что p/q — несократимая дробь. Следовательно, \(\sqrt<3>\) не является рациональным. \(\bullet\)

Таким образом, уже проблема решения простых уравнений типа x 2 =a, x 3 =a, где \(a\in\mathbb\), приводит к необходимости расширения множества рациональных чисел \(\mathbb\) путем добавления к этому множеству новых элементов, называемых иррациональными числами.

Бесконечные десятичные дроби и их приближения.

Периодичные десятичные дроби.

Известно, что любое рациональное число можно представить либо в виде конечной, либо в виде бесконечной периодической дроби. Например, рациональному числу 5/8 соответствует конечная десятичная дробь 0,625, то есть 5/8=0,625. Аналогично, рациональному числу −27/11 соответствует бесконечная периодическая десятичная дробь −2,454545… = −2(45), то есть −27/11 = −2(45).

Обратно: зная бесконечную периодическую десятичную дробь, можно найти рациональное число, представлением которого эта дробь является. Для этого используют формулу суммы бесконечно убывающей геометрической прогрессии \(a+aq+aq^2+…=\frac a<1-q>, \ \left|q\right|

Сравнение вещественных чисел.

Сравнение неотрицательных чисел.

Два неотрицательных вещественных числа

называют равными и пишут α = β при k = 0,1,2,…, то есть

Дадим определение α β. Говорят, что число α меньше числа β и пишут α \beta\right\> \ \Leftrightarrow \ \left\ b_0\right\>\vee\left\<\exists n\in\mathbb: \ a_k=b_k, \ k=\overline<0, \ n-1>; \ a_n > b_n\right\>.\nonumber$$

Из определения равенства α = β и неравенств α β следует, что для любых неотрицательных вещественных чисел α и β выполняется одно из трех условий: α = β, α β.

Отметим, что для любого неотрицательного вещественного числа α справедливо неравенство α ≥ 0.

Сравнение произвольных вещественных чисел.

Назовем модулем вещественного числа α вещественное число, обозначаемое символом |α|, представимое той же бесконечной дробью, что и α, но взятое со знаком +. Таким образом, если

$$\alpha=\pm a_0,a_1a_2…a_n…,\qquad то\qquad\left|\alpha\right|=a_0,a_1a_2…a_n…,\nonumber$$

откуда следует, что |α| — неотрицательное вещественное число при любом α.

Введем правило сравнения двух вещественных чисел α и β для случая, когда хотя бы одно из этих чисел отрицательно.

Если α — неотрицательное, β — отрицательное число, то считают, что α > β.

Если оба числа α и β отрицательны, то будем считать, что:

Легко убедиться в том, что сформулированное правило сравнения вещественных чисел в применении к рациональным числам, записанным в виде бесконечных десятичных дробей, приводит к тому же результату, что и правило сравнения рациональных чисел (п.2), представленных в виде отношения целых чисел.

Если \(\underline<\alpha>_n\), \(\underline<\beta>_n\) — n-е приближение с недостатком, а \(<\overline\alpha>_n\), \(<\overline\beta>_n\) — n-е приближение с избытком чисел α и β соответственно, то из правила сравнения вещественных чисел следует, что:

Свойства вещественных чисел, связанные с неравенствами.

Если α и β — вещественные числа, причем α Доказательство.

а) Пусть α и β — рациональные числа (α ∈ \(\mathbb\), β ∈ \(\mathbb\)). Тогда для них определены арифметические операции, и в качестве r можно взять число \(\frac<\alpha+\beta>2\), так как

$$\alpha α и α ≥ 0, то β > 0. Пусть

Пусть p — наименьший номер, при котором нарушается равенство a_k = b_k (k=0,1,2,…). Будем считать, что p > 0. Тогда

$$a_0=b_0,\qquad…,\qquad a_=b_,\qquad a_p 0\label$$

Покажем, что рациональное число r = a₀,a₁…a_p-1b_p…b_p+m-1(0) удовлетворяет условию \eqref. Из \eqref следует, что α Следствие.

Пусть δ ∈ \(\mathbb\), δ’ ∈ \(\mathbb\) и пусть существуют такие последовательности рациональных чисел <x_n> и <y_n>, что для всех n ∈ \(\mathbb\) справедливы неравенства$$x_n \ \leq \ \delta \ \leq \ \delta^, \ \leq \ y_n,\label$$

\(\circ\) Пусть равенство \eqref не выполняется; тогда из условия \eqref следует, что δ 0, и поэтому

$$\exists m\in\mathbb: \ \ \ \ \ r^,-r > \frac1<10^m>.\label$$

Из \eqref и \eqref следует, что

$$x_n \ \leqslant \ \delta

Геометрическая интерпретация вещественных чисел.

Эта прямая называется числовой прямой или числовой осью. Из аксиом геометрии и свойств вещественных чисел следует, что между множеством вещественных чисел \(\mathbb\) и числовой прямой l устанавливается взаимно однозначное соответствие: каждому вещественному числу соответствует единственная точка числовой прямой и, наоборот, каждой точке числовой прямой соответствует некоторое вещественное число. Поэтому будем в дальнейшем будем отождествлять множество \(\mathbb\) с множеством точек числовой прямой, а вещественные числа часто будем называть точками.

Условимся о следующих обозначениях для некоторых наиболее употребительных числовых множеств:

Источник