Докажите что если для положительной бесконечной десятичной дроби все приближения
Запись положительных рациональных чисел в виде десятичных дробей. Сравнение десятичных дробей. Понятие бесконечной десятичной дроби.
Десятичной называется дробь вида 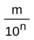
Простота сравнения и выполнения действий над десятичными дробями приводит к следующему вопросу: любую ли дробь вида 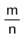
Теорема. Для того чтобы несократимая дробь 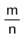
Так, например, дробь 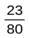
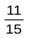
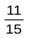
Дробь 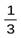
Теорема. Любое положительное рациональное число представимо бесконечной периодической десятичной дробью.
Существование чисел, отличных от рациональных; понятие положительного иррационального числа. Множество действительных чисел.
Рациональные числа − числа, представляемые в виде обыкновенной дроби a/b, где a и b − целые числа и b ≠ 0. Q = <x | x = a/b, a ∈ Z, b ∈ Z, b ≠ 0> При переводе в десятичную дробь рациональное число представляется конечной или бесконечной периодической дробью.
Будем пользоваться обозначениями:
Натуральные числа − числа, используемые при счете (перечислении) предметов: N =
1,2. Натуральные числа с включенным нулем − числа, используемые для обозначения количества предметов: N0 =
Действительные числа разделяются на рациональные и иррациональные.
Множество действительных чисел обозначается – R
Дата добавления: 2018-08-06 ; просмотров: 751 ; Мы поможем в написании вашей работы!
Бесконечные дроби и иррациональные числа
теория по математике 📈 числа и вычисления
При переводе обыкновенной дроби в десятичную можно получить конечную периодическую или бесконечную десятичные дроби (кроме простой десятичной, разумеется).
Конечная десятичная дробь
Конечная десятичная дробь – десятичная дробь с конечным числом знаков после запятой, то есть когда у аналога обыкновенной дроби числитель без остатка делится на знаменатель.
Пример №1. ¾ — делим 3 на 4 и получаем 0,75.
Пример №2. 31 /50 делим 31 на 50 и получаем 0,62.
Пример №3. 3 /25 делим 3 на 25 и получаем 0,12.
Периодическая десятичная дробь
Периодическая десятичная дробь – дробь, у которой после запятой (в дробной части) присутствует бесконечный повтор одной цифры или сочетания нескольких одинаковых цифр.
Пример №4. 7 /12 При делении 7 на 12 получается 0,5833333…, где постоянно повторяется цифра 3, запись делают следующим образом: 0,58(3); читается эта дробь следующим образом: нуль целых пятьдесят восемь сотых и три в периоде.
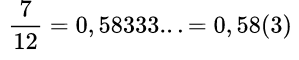
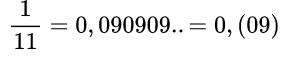
Иррациональные числа — числа, которые не могут быть представлены в виде обыкновенной дроби.
Значение какого из выражений является рациональным числом?
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
Данный вариант ответа нам подходит.
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из данных чисел является рациональным?
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
Рассмотри каждое из них:
Следовательно, число √0,81 является рациональным, остальные же числа
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
pазбирался: Даниил Романович | обсудить разбор | оценить
Значение какого из данных ниже выражений является наибольшим?
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
Переносим 3 под корень:
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
Возводим 6,5 в квадрат:
Посмотрим на все получившиеся варианты:
Следовательно, правильный ответ первый.
pазбирался: Даниил Романович | обсудить разбор | оценить
Для решения этого задания достаточно представлять себе значения чисел меньше и больше заданного, корни которых подлежат вычислению.
Значит, нам подходит третий вариант ответа — √38.
pазбирался: Даниил Романович | обсудить разбор | оценить
Докажите что если для положительной бесконечной десятичной дроби все приближения
Докажите, что в любой бесконечной десятичной дроби можно так переставить цифры, что полученная дробь станет рациональным числом.
Подсказка
Рассмотрите отдельно те цифры, которые встречаются конечное число раз и те, которые встречаются бесконечно много раз.
Решение
Дробь выражает рациональное число в том и только случае, когда она периодическая, начиная с некоторого знака. Цифры от 0 до 9 разделим на два класса: в первый класс включим те цифры, которые встречаются в исходной дроби конечное число раз, во второй класс – те, которые встречаются в исходной дроби бесконечное число раз. Начнем выписывать периодическую дробь, которая может быть получена из исходной перестановкой цифр. Вначале после нуля и запятой напишем в произвольном порядке все цифры из первого класса – каждую столько раз, сколько она встречается в записи исходной дроби. Записанные цифры первого класса будут являться предпериодом дроби. Далее запишем в некотором порядке по одному разу цифры из второго класса. Эту комбинацию объявим периодом и будем повторять её бесконечное число раз. Таким образом, мы выпишем искомую периодическую дробь.
Источники и прецеденты использования
| web-сайт | |
| задача | |
| книга | |
| Автор | Алфутова Н.Б., Устинов А.В. |
| Год издания | 2002 |
| Название | Алгебра и теория чисел |
| Издательство | МЦНМО |
| Издание | 1 |
| глава | |
| Номер | 5 |
| Название | Числа, дроби, системы счисления |
| Тема | Системы счисления |
| параграф | |
| Номер | 1 |
| Название | Рациональные и иррациональные числа |
| Тема | Дроби |
| задача | |
| Номер | 05.008 |
0. Десятичные дроби и действительные числа
Дроби, у которых знаменатель представляет собой степень десяти, называются десятичными дробями. Записываются они особым образом:
Попытка записать любую обыкновенную дробь в виде десятичной иногда приводит к бесконечной десятичной дроби. Например, разделив «уголком», получим:
В этом случае бесконечная последовательность цифр содержит период – один и тот же повторяющийся набор цифр. Такие дроби называются бесконечными периодическими десятичными дробями. Можно доказать, что любая обыкновенная дробь записывается в виде бесконечной периодической десятичной дроби. Обратное также верно: любая бесконечная периодическая десятичная дробь представляет собой десятичную запись некоторой обыкновенной дроби.
Рассмотрим на примере, как найти последнюю. Превратим в обыкновенные дроби числа Q = 0,777… и Р = 0,999… Умножим на 10, получим:
1) 10Q = 7,777(7), откуда 10Q = 7 + Q; т. е. 9Q = 7, или 
2) 10Р = 9,999(9), откуда 10Р = 9 + Р, т. е. 9Р = 9, или Р = 1.
Замечание. Число 1 можно записать в виде 1,000…, т. е. с периодом 0; аналогично 0,24 = 0,24000… и т. д.
Имеют ли смысл бесконечные непериодические десятичные дроби?
Рассмотрим равнобедренный прямоугольный треугольник, длина катетов которого равна 1. Обозначим длину гипотенузы Х. По теореме Пифагора
Докажем, что корни этого уравнения не являются рациональными числами. Предположим противное, что корнем (1) является дробь 




Т. к. в правую часть (2) входит множитель 2, то А2 – число четное, следовательно, число А – также четное, его можно записать в виде А = 2×С. Подставим это выражение в (2), получим (2×С)2 = 2×B2, или, сократив на 2, 2×С2 = B2. Отсюда следует, что число B2 также четное, следовательно, B – тоже четно. Поскольку А и B четные, дробь 

Найдем приближенные значения числа 
На первых четырех позициях соответствующие цифры одинаковы, а 6>5.
Единственное исключение из этого правила – не рассматривать периодические дроби с периодом 9. всякую такую дробь можно заменить равной ей конечной десятичной дробью, например: 0,999…=1; 0,42999…=0,43; 2,65999…=2,66.
Свойства операций сложения и умножения действительных чисел:
Правило округления десятичных дробей, например, до сотых:
0,811»0,81; 0,812»0,81;…; 0,815»0,82; 0,816»0,82;…; 0,819»0,82.
Действия со степенями:
По определению: А0 = 1, АN = A×A×A×…×A (N сомножителей); 
Число, которое при возведении в степень N даёт а, называется корнем степени N из А. Если число N нечетное, то существует только один действительный корень степени N из числа А; его обозначают 




Степень с дробным показателем определяется так:
Имеют смысл и выражения вида Ах, где Х – любое действительное число, например, 

Стандартная форма записи чисел реализуется в виде произведения двух множителей, первый из которых – между 1 и 10, а второй является степенью десяти, например
243507 = 2,43507×105; 0,184 = 1,84×10-1 и т. д.
Такая форма используется при вычислениях с калькулятором, особенно если не хватает разрядов для точных вычислений. Она также используется в компьютерах.
1.2. Десятичные дроби и действительные числа
Дроби, у которых знаменатель представляет собой степень десятки, т. е. 10, 102 = 100, 103 = 1000 и т. д., называются Десятичными дробями. Записываются они особым образом:
Попытка записать любую обыкновенную дробь в виде десятичной дроби приводит иногда к Бесконечной десятичной дроби. Например, разделив «уголком», мы получим:
Как видно, получающаяся бесконечная последовательность цифр содержит так называемый Период — один и тот же повторяющийся набор цифр. Поэтому полученные десятичные дроби называют Бесконечными периодическими десятичными дробями. Можно доказать, что любая обыкновенная дробь записывается в виде бесконечной периодической десятичной дроби. Обратное также верно: любая бесконечная периодическая десятичная дробь представляет собой десятичную запись некоторой обыкновенной дроби. Как найти последнюю, поясним на примере.
Пример. Превратим в обыкновенные дроби числа Q = 0,777. и Р = 0,999.
Умножив на 10, получаем:
1) 10Q = 7,777. = 7 + Q, откуда 9Q = 7 и Q = 
Проверьте результат, превратив 7/9 в десятичную дробь.
2) 10P = 9,999. = 9 + р, откуда 9Р = 9 и Р = 1. Заметим, что 1 можно записать в виде бесконечной десятичной дроби с периодом 0: 1,000. ; аналогично, 0,24 = 0,24000. 3,5 = 3,5000. и т. п.
8. С помощью калькулятора и «вручную» превратите данную обыкновенную дробь в бесконечную периодическую десятичную дробь и укажите период: 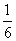




9. Превратите бесконечную периодическую десятичную дробь в обыкновенную: 1,888. ; 0,1212. ; 0,444.
Решив эти примеры, каждый будущий юрист задаст себе вопрос: а имеют ли смысл бесконечные Непериодические десятичные дроби?
Рассмотрим равнобедренный прямоугольный треугольник, длина катетов которого равна единице. Обозначим длину гипотенузы через Х. По теореме Пифагора

Докажем, что корни этого уравнения не являются рациональными числами. В самом деле, предположим противное, т. е. что корнем уравнения (1) является дробь 


Подставляя 


Так как в правую часть равенства (2) входит множитель 2, то А2 — число четное. Следовательно, число А также четное и его можно записать в виде А = 2С. Подставив в (2), получим (2С)2 = 2B2 или, сократив на 2, 2С2 = B2. Отсюда следует, что число B2 также является четным. Но тогда четным будет и число B. Теперь, поскольку оба числа А и B получились четными, дробь 


Результат наших рассуждений можно сформулировать иначе: квадратный корень из числа 2 не является рациональным числом, т. е. бесконечной периодической десятичной дробью.
Будем искать приближенные значения числа Х = 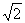
0,999. = 1, 0,42999. = 0,43, 2,65999. = 2,66 и т. п. (см. пример на с. 15).
Напомним свойства операций сложения и умножения действительных чисел:
Переместительность или коммутативность:
Сочетательность или ассоциативность (для сложения):
Сочетательность или ассоциативность (для умножения):
Распределительность или дистрибутивность:
Числовые множества N, Z, Q, R являются примерами так называемых Числовых систем, которые имеют специальные названия. Например, говорят Кольцо целых чисел, поле рациональных чисел, поле действительных чисел. Эти термины мы обсуждаем в восьмой главе. Там мы покажем, в частности, что поле действительных чисел можно расширить и получить так называемые Комплексные числа.
ПРАВИЛО ОКРУГЛЕНИЯ ДЕСЯТИЧНЫХ ДРОБЕЙ
Поясним на примере. Следующие десятичные дроби мы округляем до сотых долей:
10. Вычислите с помощью калькулятора и округлите до тысячных:
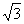









11. Найдите 3!, 4!, 5!, 6!, 7!, 81, 9!, 10!.
12. Расставьте правильно знаки > или 0, запишите ответ в виде бесконечной периодической десятичной дроби и округлите его до сотых.
ДЕЙСТВИЯ СО СТЕПЕНЯМИ
Из этого определения следует, что для любых натуральных чисел Т И п справедливы следующие формулы:
Am an = am+n, (an)m = amn, an bn = (Ab)N.
Число, которое при возведении в степень П дает A, называется корнем степени N из А. Если число П нечетное, то существует только один корень степени П из числа А, Который обозначается 



Степень с дробным показателем определяется так:
Оказывается, что имеют смысл и выражения вида Aх, Где Х — любое действительно число, например 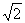

При различных вычислениях большие числа удобно записывать в так называемой Стандартной форме, т. е. в виде произведения двух множителей, первый из которых заключен между числами 1 и 10, а второй представляет собой степень десятки: 243507 = 2,43507 • 105, 0,184 = 1,84 • 10–1 и т. д. Стандартную форму используют при работе с калькулятором, в особенности тогда, когда не хватает разрядов для точных вычислений. Например,
243507 • 1385462 = 2,43507 • 105 • 1,385462 • 106 = (2,43507 • 1,385462) • 1011 » 3,37369695 • 1011;
317 = 316 • 3 = (34)4 • 3 = (81)4 • 3 = (6581)2 • 3 = 3 • (6,581 • 103)2 = 3 • (6,581)2 • (103)2 » 129,140163 • 106.
2. Вычислите, округляя в каждом действии результат до тысячных; окончательный результат округлите до сотых:
3. Найдите корни квадратного уравнения и округлите результат до сотых:
Одна сотая доля какого-либо количества называется Процентом. Например, в городе N всего 300 судей, следовательно, 3 судьи — это 1%, 6 судей — 2% и т. д.
Подумайте, сколько тверских судей составляют 4% от их общего числа? (В Твери 145 судей.)
Другой пример. Некто утаил прибыль в размере 10 млн. руб. Какую сумму недополучила казна, если налог на прибыль составляет 22%?
Решение: 10 млн • 
4. За год в области совершено 6720 преступлений. Из них тяжких — 33; в состоянии алкогольного опьянения — 3262; связанных с дорожно-транспортными происшествиями — 1310. После завершения следствия переданы в суд 4520 дел; по 3816 из них уже вынесены приговоры, причем половина из последних — обвинительные; из всех обвинительных приведены в исполнение 40%. Заполните до конца следующую таблицу:
В первом столбце проставьте соответствующие абсолютные значения, а во втором укажите, какой процент они составляют от общего числа преступлений.