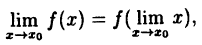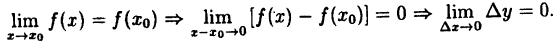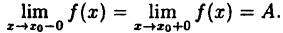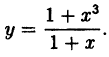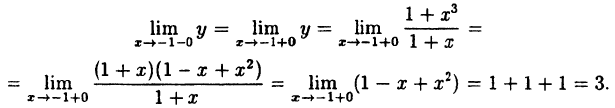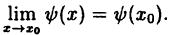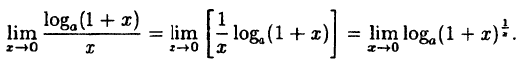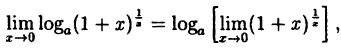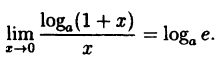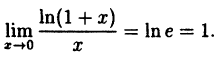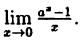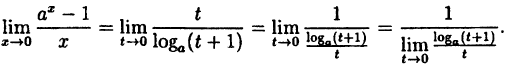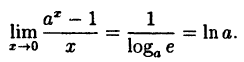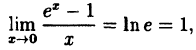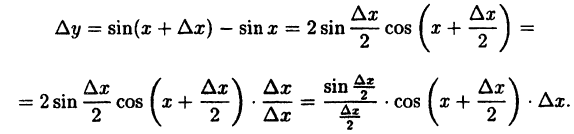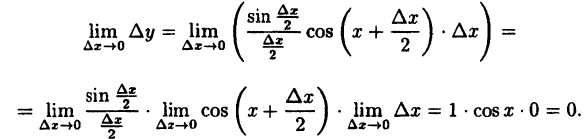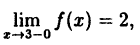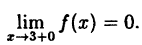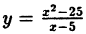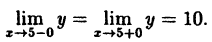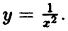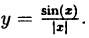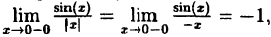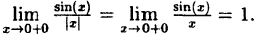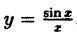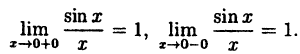Докажите что функция f x x2 10x
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Непрерывность функций с примерами решения и образцами выполнения
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 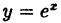
Решение:
Чтобы доказать, что функция 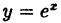
Таким образом, доказано, что функция 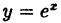
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 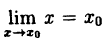
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 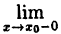
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
Используя теоремы о пределе суммы и произведения функции, получим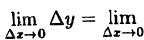
Следовательно, функция у = х³ непрерывна при — ∞ Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 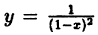
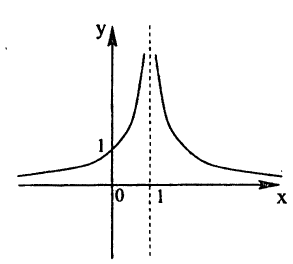
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию
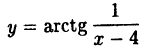
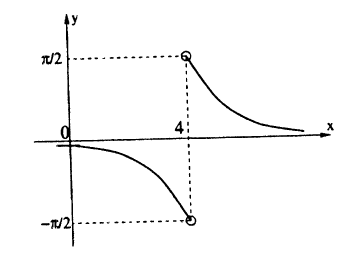
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —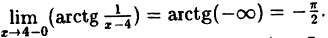
Предел справа — 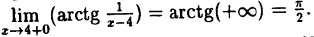
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 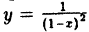
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀:
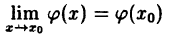
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:




Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 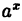
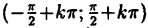
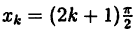
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( 

но 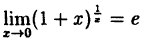
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 
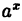
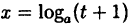
Так как на основании результата, полученного в предыдущем примере, 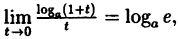
(10.6)
В частности, если а = е, имеем
т.е. у = 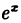
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
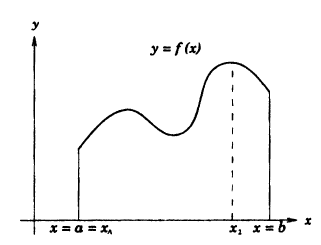
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
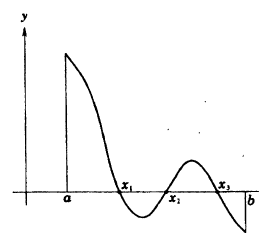
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Теорема:
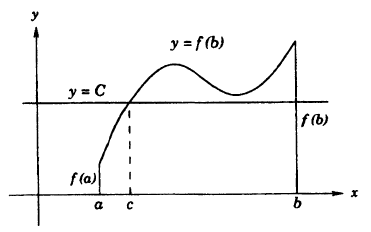
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 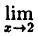
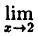
3) этот предел равен значению функции в точке х = 2
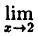
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 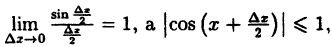
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
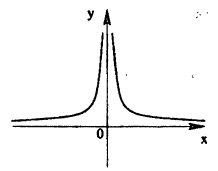
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
Пример:
Исследовать на непрерывность функцию 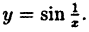
Решение:
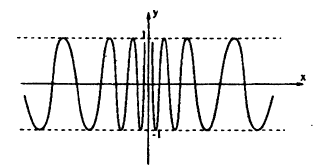
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 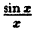
Если доопределить функцию 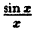
f(х) =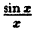
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций



Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института