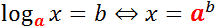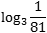Докажите что log2 2 1

Логарифмы

Определение логарифма

Понятие логарифма и основного логарифмичесгого тождества

Понятие логарифма и основного логарифмическое тождества состоят в тесной зависимости, т.к. определение логарифма в математической записи и является основным логарифмическим тождеством.

Основное логарифмическое тождество вытекает из определения логарифма:

Логарифмом называют показатель степени n, при возведении в которую числа а получают число b.

Показательное уравнение a^n=b при a > 0, a ne 1 не имеет решений при неположительном b и имеет единственный корень при положительном b. Этот корень называется логарифмом числа b по основанию а и записывают:

Основное логарифмическое тождество

4 log₂ 7 =2 2 log₂ 7 = (2 log₂ 7 ) 2 = 7 2 = 49

2 1 + log₂ 7 = 2 · 2 log₂ 7 = 2 · 7 = 14

Что такое логарифм и как его посчитать

Логарифм имеет следующий вид:

где a – это основание логарифма,

b – это аргумент логарифма

Чтобы узнать значение логарифма приравняем его к X. и преобразовываем в и преобразовываем в Запомните, что именно основание (оно выделено красным) возводится в степень.

Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!

Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:

Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.

Два очевидных следствия определения логарифма

log a 1 = 0 ( a > 0, a ≠ 1 )

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень – единицу.

Логарифм. Свойства логарифма (корень логарифма, смена основания).

Корень логарифма из положительного числа равен логарифму подкоренного выражения, деленному на показатель корня/Логарифм. Свойства логарифма (корень логарифма, смена основания).

Использование свойств логарифмов при решении логарифмических уравнений и неравенств

Для того, чтобы не ошибаться при решении логарифмических уравнений и неравенств, свойства логарифмов, перечисленные в предыдущем разделе, следует применять внимательно и аккуратно.

Например, если при решении уравнения или неравенства требуется преобразовать выражение

следует применять формулу

поскольку в противном случае можно потерять корни.

По той же причине при преобразовании выражений

log_a ( f (x) g (x)) и

следует использовать формулы:

Степень можно выносить за знак логарифма

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

log a ( f ( x ) 2 = 2 log a f ( x )

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть – только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Логарифмы со специальным обозначением

Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.

Виды логарифмов

log_a b – логарифм числа b по основанию a ( a > 0, a ≠ 1, b > 0)

lg b – десятичный логарифм (логарифм по основанию 10, a = 10).

Сумма логарифмов. Разница логарифмов

Логарифмы с одинаковыми основаниями можно складывать: Логарифмы с одинаковыми основаниями можно вычитать: Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!

Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!

Вынесение показателя степени из логарифма

Вынесение показателя степени из логарифма:

Переход к новому основанию

Когда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.

Разберем на примере.

Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:

Теперь применим переход к новому основанию для второго логарифма: Подставим полученные результаты в исходное выражение:

Десятичные и натуральные логарифмы

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например,

lg ( x y ) = lg x + lg y ( x > 0, y > 0 )

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e – иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам:

log a b = lg b lg a = ln b ln a ( a > 0, a ≠ 1, b > 0 )

Вычисление логарифма равносильно решению показательного уравнения

при условии a > 0, a ≠ 1; b > 0, где

при условии a > 0, a ≠ 1; b > 0, где

Найти логарифм: log ₄ 8

Обозначим log₄ 8 через x :

Перейдем к показательному уравнению:

Сведем показательное уравнение к основе 2 и решим его:

Найти x если : log _x 125 = 3 2

За определением логарифма имеем:

x = (5 3 ) 2/3 = 5 3·2/3 = 5 2 = 25

Формулировки и доказательства свойств

Покажем примеры использования свойства логарифма произведения: log₅(2·3)=log₅2+log₅3 и .

Приведем пример использования этого свойства логарифма: .

Вот пример использования этого свойства: .

Покажем пару примеров применения этого свойства логарифмов: и .

Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .

Осталось доказать свойства сравнения логарифмов.

Область допустимых значений (ОДЗ) логарифма

Теперь поговорим об ограничениях (ОДЗ – область допустимых значений переменных).

Мы помним, что, например, квадратный корень нельзя извлекать из отрицательных чисел; или если у нас дробь, то знаменатель не может быть равен нулю. Подобные ограничения есть и у логарифмов:

Поэтому и отрицательные основания проще выбросить, чем возиться с ними.

Ну а поскольку основание a у нас бывает только положительное, то в какую бы степень мы его ни возводили, всегда получим число строго положительное. Значит, аргумент должен быть положительным. Например, не существует, так как ни в какой степени не будет отрицательным числом (и даже нулем, поэтому тоже не существует).

В задачах с логарифмами первым делом нужно записать ОДЗ. Приведу пример:

Но если сразу взять и записать оба этих числа в ответе, можно получить 0 баллов за задачу. Почему? Давайте подумаем, что будет, если подставить эти корни в начальное уравнение?

– это явно неверно, так как основание не может быть отрицательным, то есть корень – «сторонний».

Чтобы избежать таких неприятных подвохов, нужно записать ОДЗ еще до начала решения уравнения:

10 примеров логарифмов с решением

1. Найти значение выражения 2. Найти значение выражения 3. Найти значение выражения 3. Найти значение выражения 4. Найти значение выражения 5. Найти значение выражения 5. Найти значение выражения 6. Найти значение выражения Сначала найдем значение Сначала найдем значение Для этого приравняем его к Х:Тогда изначальное выражение принимает вид:

7. Найти значение выражения 7. Найти значение выражения Преобразуем наше выражение: Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выражения 8. Найти значение выражения Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов: 9. Найти значение выражения 9. Найти значение выражения Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:

10. Найти значение выражения Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄: Обращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log₂16. Поэтому сначала найдем значение log₂16, а затем подставим полученный результат в log₄:

Надеюсь, теперь вы разобрались, что такое логарифм.

Источник

Что такое логарифм

Логарифмы всегда считались сложной темой в школьном курсе математики. Существует много разных определений логарифма, но большинство учебников почему-то используют самые сложные и неудачные из них.

Мы же определим логарифм просто и наглядно. Для этого составим таблицу:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Например, 2 3 = 8 ⇒ log₂ 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log₂ 64 = 6, поскольку 2 6 = 64.

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log2 2 = 1	log2 4 = 2	log2 8 = 3	log2 16 = 4	log2 32 = 5	log2 64 = 6

Если взять калькулятор и посчитать, чему равны такие логарифмы, то получатся очень длинные числа. Взгляните сами:
log₂ 5 = 2,32192809.
log₃ 8 = 1,89278926.
log₅ 100 = 2,86135311.

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log₂ 5, log₃ 8, log₅ 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

Как считать логарифмы

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log _a x = b ⇒ x > 0, a > 0, a ≠ 1.

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log₁₀ x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log _e x

Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Источник

Логарифм. Как вычислить логарифм?

Логарифмом положительного числа \(c\) по основанию \(a\) \((a>0, a\neq1)\) называется показатель степени \(b\), в которую надо возвести основание \(a\), чтобы получить число \(c\) \((c>0)\), т.е.

Объясним проще. Например, \(\log_<2><8>\) равен степени, в которую надо возвести \(2\), чтоб получить \(8\). Отсюда понятно, что \(\log_<2><8>=3\).

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

Как вычислить логарифм?

а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:

в) В какую степень надо возвести \(\sqrt<5>\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!

г) В какую степень надо возвести \(\sqrt<7>\), чтобы получить \(\sqrt<7>\)? В первую – любое число в первой степени равно самому себе.

В сложных случаях для вычисления логарифма удобно переводить его в показательное уравнение.

Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма:
\(\log_=b\) \(\Leftrightarrow\) \(a^=c\)

Слева воспользуемся свойствами степени: \(a^\cdot a^=a^\) и \((a^)^=a^\)

Основания равны, переходим к равенству показателей

Умножим обе части уравнения на \(\frac<2><5>\)

Получившийся корень и есть значение логарифма

Зачем придумали логарифм?

Чтобы это понять, давайте решим уравнение: \(3^=9\). Просто подберите \(x\), чтобы равенство сработало. Конечно, \(x=2\).

А теперь решите уравнение: \(3^=8\).Чему равен икс? Вот в том-то и дело.

Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как \(x=\log_<3><8>\).

\(4^<5x-4>\) и \(10\) никак к одному основанию не привести. Значит тут не обойтись без логарифма.

Воспользуемся определением логарифма:
\(a^=c\) \(\Leftrightarrow\) \(\log_=b\)

Зеркально перевернем уравнение, чтобы икс был слева

И не пугайтесь логарифма, относитесь к нему как к обычному числу.

Поделим уравнение на 5

Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg\).

Основное логарифмическое тождество

У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:

Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.

Вспомним краткую запись определения логарифма:

Пример: Найдите значение выражения \(36^<\log_<6><5>>\)

Вот теперь спокойно пользуемся основным логарифмическим тождеством.

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_<2><4>\) равен двум. Тогда можно вместо двойки писать \(\log_<2><4>\).

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как \(\log_<2><8>\), или как \(\log_<3><27>\), или как \(\log_<4><64>\)… Здесь мы как аргумент пишем основание в кубе:

Источник