Докажите что медианы равнобедренного треугольника
Определение и свойства медианы в равнобедренном треугольнике
В данной статье мы рассмотрим определение и свойства медиан, проведенных к основанию и боковым сторонам равнобедренного треугольника, а также разберем пример решения задачи для закрепления теоретического материала.
Определение медианы
Медианой называется отрезок в треугольнике, который соединяет вершину и середину противоположной стороны.
Треугольник является равнобедренным, если две его стороны равны (боковые), а третья сторона – это основание фигуры.
Свойства медианы в равнобедренном треугольнике
Свойство 1
Медиана в равнобедренном треугольнике, проведенная к основанию, одновременно является высотой, опущенной на основание, и биссектрисой угла, из которого она проведена.
Свойство 2
В равнобедренном треугольнике медианы пресекаются в одной точке (центр тяжести) и делятся в этой точке в отношении 2:1.
Свойство 3
Медиана делит равнобедренный треугольник на 2 равных по площади (равновеликих) треугольника. Следовательно, S1 = S2.
Свойство 4
Если провести три медианы в равнобедренном треугольнике, образуются 6 равновеликих треугольников (S1 = S2 = S3 = S4 = S5 = S6).
Свойство 5
Длину медианы в равнобедренном треугольнике, проведенную к основанию, можно найти по следующей формуле:
Свойство 6
Данной свойство, в отличие от перечисленных выше, не относится к медиане, опущенной на основание фигуры. Оно гласит:
Медианы, проведенные к боковым сторонам равнобедренного треугольника, равны между собой.
AF = CE, следовательно, AE = EB = BF = FC.
Пример задачи
Основание равнобедренного треугольника равняется 7 см, а боковая сторона – 12 см. Найдите длину медианы, проведенной к основанию фигуры.
Решение
Воспользуемся формулой, представленной в Свойстве 5, подставив в нее известные нам по условиям задачи значения:
Если две медианы треугольника равны
Если две медианы треугольника равны, то этот треугольник — равнобедренный.
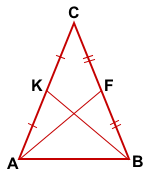
Доказать: ΔABC — равнобедренный
Так как AF и BK — медианы треугольника ABC, то точки F и K — середины отрезков BC и AC соответственно.
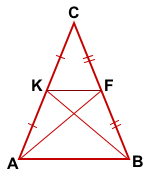
Таким образом, AKFB — трапеция.
Половины отрезков равны, значит равны и сами отрезки: AC=BC.
Что и требовалось доказать.
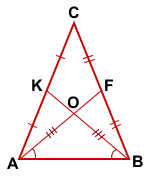
Так как медианы треугольника точкой пересечения делятся в отношении 2 к 1, считая от вершины, то
Так как AF=BK (по условию), то AO=BO.
Следовательно, треугольник AOB — равнобедренный с основанием AB.
Рассмотрим треугольники ABF и BAK.
2) сторона AB — общая,
3) ∠OAB=∠OBA (по доказанному).
Значит треугольники ABF и BAK равны ( по 1 признаку).
Из равенства треугольников следует равенство соответствующих углов:∠ABF=∠BAK.
Отсюда треугольник ABC — равнобедренный с основанием AB (по признаку).
Равнобедренный треугольник: свойства, признаки и формулы
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Для доказательства следующих теорем нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
В каждом из доказательств мы пользуемся признаком равенства треугольников, вот и повод их повторить.
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Урок математики по теме «Свойство медианы равнобедренного треугольника». 7-й класс
Разделы: Математика
Класс: 7
Тип урока: урок изучения нового материала и первичное его закрепление
Оборудование: проектор, компьютер, чертёжные инструменты, тетради, карточки.
1. Организационный момент
Цель: мотивация
Учитель: Ребята, я очень рада очередной встречи с вами на нашем уроке геометрии. Это обычный и не совсем обычный урок. Поэтому девизом нашего урока будут служить слова Алексея Ивановича Маркушевича,редактора «Энциклопедии элементарной математики»:
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели». (Презентация. Слайд 2)
Сегодня у всех вас ребята есть возможность этим заняться. Поэтому я прошу вас быть очень внимательными. Мы начинаем урок и продолжаем изучать свойства равнобедренного треугольника, но для начала повторим всё, что мы знаем об этом необычном треугольнике. (Слайд 3)
2. Актуализация знаний
Цель: повторить основные понятия, связанные с данной темой и позволяющие легкому усвоению свойства медианы равнобедренного треугольника.
Учитель: Ребята, внимание на экран. Ответьте, пожалуйста, на следующие вопросы:
Задание №1 (устно):
а) Какие из треугольников являются равнобедренными? Почему? (Слайд 4)
б) В равнобедренных треугольниках назовите основание и боковые стороны.
в) Назовите равные углы. Почему?
Задание №2 (устно): (Слайд 5)
а) Назовите треугольник, на котором изображена биссектриса. Почему?
б) Назовите треугольник, на котором изображена медиана. Почему?
в) Назовите треугольник, на котором изображена высота. Почему?
Учитель: Открываем тетради, записываем число. «Классная работа».
К доске приглашается один ученик а остальные в тетрадях выполняем следующее задание:
Задание №3 (в тетрадях): Начертите равнобедренный треугольник АВС, с основанием АВ.
Проведите в данном треугольнике медиану из вершины С к основанию АВ.
На этом же чертеже проводим высоту из вершины С к основанию АВ. И биссектрису угла С.
(В процессе построения учитель ведёт диалог с учеником у доски и всем классом, объясняя каждый шаг построения).
Учитель: Ребята, что вы увидели? Какой вывод можно сделать, исходя из построения?
(Ребята предлагают ответы. В ходе обсуждения выясняется, что не все получили совпадение медианы, биссектрисы и высоты.)
Как говорил Дьёрдь Пойавенгерский,швейцарскийи американский математик. (Слайд 6)
Лучший способ изучить что-либо – это открыть самому.
Мы это с вами сейчас сделали. Но геометрия – эта наука, в которой нельзя делать вывод, исходя из решения одной задачи. Всё, кроме аксиом, необходимо доказать. Поэтому переходим к изучению нового материала.
3. Постановка учебной задачи. Изучение нового материала
Цель: сформулировать и доказать свойство медианы равнобедренного треугольника.
Учитель: Ребята, запишите в тетрадях тему нашего урока «Свойство медианы равнобедренного треугольника».Ребята, скажите, пожалуйста, изучив сегодняшнюю тему, на какой вопрос в конце урока вы сможете ответить?
(Ребята предлагают ответы, а учитель подводит итог и называет цель урока.)
Да, действительно цель нашего урока сформулировать и доказать свойство медианы равнобедренного треугольника, и на примерах показать его применение.
Учитель: Запишите на полях номер теоремы 3.5. (Под диктовку учащиеся записывают формулировку.)
В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.(Все делают чертёж равнобедренного треугольника. Работа по формулировке. Ребята формулируют теорему, используя «ЕСЛИ» и «ТО» и соответственно делая вывод, что в теореме является условием, а что заключением. Затем записывают «дано» и «доказать».) (Слайд 7)
Δ АВС – равнобедренный,
АВ – основание,
СD – медиана
СD – биссектриса,
СD – высота
Доказательство теоремы сегодня необычное. Ваша задача внимательно слушать, внимательно следить по чертежу.
Учитель: (доказательство в стихах)
В моей любимой теореме
Смысл совсем, совсем простой.
Медиана в равнобедренном треугольнике –
Является биссектрисой и высотой.
Рассмотрим– необычный.
На вид он очень симпатичный.
АВ основанием является
Треугольник равнобедренным называется.
Нам СD – медиана дана.
Интересным свойством обладает она.
Смотри на чертёж, и увидишь ты сам
Как медиана делит основание пополам.
Нам доказать с вами очень надо,
Что медиана является биссектрисой и высотой.
За это доказательство ждёт нас награда.
Пятёрка в дневник, приз очень простой.
Итак, приступаем к доказательству.
Прошу внимательно следить
Хотя здесь букв всего четыре
Ни одну нельзя нам упустить.
и СВD равны
В этом нет сомнения.
Первый признак применить
Надо непременно.
АС = СВ по условию ясно
АD = ВD, ведь D середина, не спорьте напрасно.А =
В, как углы при основании
(Ничего не выпало у нас из внимания)
Посмотрим внимательно мы на чертёж
Вывод практически готов.
Равенство треугольников за собой влечёт
Равенство углов, честь им и почёт.
Так какАСD =
ВСD, то СD – биссектриса,
Часто ребята зовут её «крысой».
Углы АDС и ВDС равны вот и прекрасно
Ещё они смежные – по чертежу это ясно.
Углы то прямые и замечательно.
Теперь теорему запомним обязательно.
Не доказательство, а красота.
Смотрите СD к тому же высота.
Вывод: Наше сегодняшнее открытие, что медиана, биссектриса и высота совпадают, получило подтверждение данной теоремой. И тут возникает вопрос, ответ на который уже давно дала наша замечательная наука геометрия. Ребята, вы знаете, что в треугольнике три стороны и три угла. Соответственно можно провести три медианы, биссектрисы и высоты. Как вы думаете, утверждение «медиана, проведённая к боковой стороне, является биссектрисой и высотой» будет верно или нет!
Выслушав ответы учащихся, учитель делает вывод.
4. Первичное закрепление нового материала
Цель: Показать на примерах применение теоремы при решении задач.
Учитель: Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение. (В. Произволов) (слайд 8)
Все внимание на экран. Решаем задачу устно. (Работает весь класс)
Задача № 3
В равнобедренном треугольнике АВС с основанием АС = 12см и 30.07.2014
Свойства равнобедренного треугольника
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника (рис. 63, а).
Треугольник, все стороны которого равны, называется равносторонним (рис. 63, б).
Докажем две теоремы о свойствах равнобедренного треугольника.
| В равнобедренном треугольнике углы при основании равны. |
Рассмотрим равнобедренный треугольник АВС с основанием ВС и докажем, что ∠B = ∠C. Пусть AD — биссектриса треугольника АВС (рис. 64). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠1 = ∠2, так как AD — биссектриса). В равных треугольниках против равных сторон лежат равные углы, поэтому ∠B = ∠C. Теорема доказана.
| В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой. |
Обратимся снова к рисунку 64, на котором 
Из равенства треугольников ABD и ACD следует, что BD = DC и ∠3 = ∠4. Равенство BD = DC означает, что точка D — середина стороны ВС, и поэтому AD — медиана треугольника АВС. Так как углы 3 и 4 — смежные и равны друг другу, то они прямые. Следовательно, отрезок AD является также высотой треугольника АВС. Теорема доказана.
Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведённые к основанию, совпадают. Поэтому справедливы также утверждения:







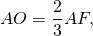
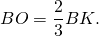








 – необычный.
– необычный.  и СВD равны
и СВD равны  А =
А = 
