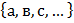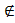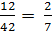Докажите что множества равны 8 класс мерзляк
КР-1 Множества и операции над ними. Алгебра 8 (угл)
КР-1 Множества и операции над ними. Алгебра 8 (угл)
Алгебра 8 класс. Контрольная работа КР-1 Множества и операции над ними для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + ОТВЕТЫ. Цитаты из пособия «Алгебра 8 класс Самостоятельные и контрольные работы» (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях.
Контрольная работа № 1 по алгебре в 8 классе (угл.)
КР-1 Множества и операции над ними
ОТВЕТЫ на Контрольную № 1
ВАРИАНТ 1.
№ 1. A = <2, –7>.
№ 2. <7>, <1>, <1, 7>, ∅.
№ 3. 1) верно, 2) не верно, 3) не верно, 4) верно
№ 4. 1) верно, 2) не верно, 3) не верно, 4) верно, 5) верно, 6) верно.
№ 5. Ответ: 1 человек.
№ 6. А = В, если их объединение и пересечение совпадает. A ∪ B =
№ 7. При n = 1 ⇒ 1/2; при n = 2 ⇒ 1/4; при n = 3 ⇒ 1/6 и так далее. Все элементы множества различны и образуют числовую последовательность. Значит, счётно.
№ 8. 1 и 25 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
ВАРИАНТ 2.
№ 1. A = <4, –6>.
№ 2. <5>, <1>, <1, 5>, ∅.
№ 3. 1) не верно, 2) не верно, 3) верно, 4) верно
№ 4. 1) не верно, 2) верно, 3) верно, 4) верно, 5) не верно, 6) не верно.
№ 5. Ответ: 5 человек.
№ 6. C = D, если их объединение и пересечение совпадает. C ∪ D =
№ 7. При k = 1 ⇒ 1/3; при k = 2 ⇒ 1/6; при k = 3 ⇒ 1/9 и так далее. Все элементы множества различны и образуют числовую последовательность. Значит, счётно.
№ 8. 1 и 27 (начало и конец) — нечетные числа. Значит, нечетных будет больше.
Алгебра 8 класс. Контрольная работа № 1 «Множества и операции над ними» для УМК Мерзляк, Поляков (УГЛУБЛЕННОЕ изучение) + ОТВЕТЫ. Цитаты из пособия «Алгебра 8 класс Самостоятельные и контрольные работы» (авт. Мерзляк, Полонский, Рабинович и др., изд-во «Вентана-Граф») использованы в учебных целях.
1. Множество. Подмножество — Алгебра (угл.)
Алгебра 8 класс. Мерзляк, Поляков (угл.)
Часто в повседневной жизни объединённые по некоторому признаку объекты мы называем группой, объединением, коллекцией, совокупностью и т. п. Для этих слов в математике существует синоним множество.
Приведём несколько примеров множеств:
Отдельные множества в математике имеют названия:
Множества, элементами которых являются числа, называют числовыми множествами. Для некоторых числовых множеств используют специальные обозначения:
Если элемент а принадлежит множеству A, то пишут а ∈ А (читают: «а принадлежит множеству A»). Если элемент b не принадлежит множеству A, то пишут b ∉ А (читают: «b не принадлежит множеству A»).
Например, 12 ∈ N, –3 ∉ N, 2/3 ∈ Q, 2/3 ∉ Z, a ∈ <a, b, c>.
Чаще всего множество задают одним из двух способов.
Первый способ. Множество задают перечислением всех его элементов.
Например, если М — множество натуральных чисел, меньших 5, то пишут М = <1, 2, 3, 4>.
Второй способ. Указывается характеристическое свойство элементов множества, т. е. свойство, которым обладают все элементы данного множества и только они.
Например, если х — произвольный элемент множества А, которое задано с помощью характеристического свойства его элементов, то пишут А = <х | …>. После вертикальной черты указывают условие, которому должен удовлетворять элемент х, чтобы принадлежать множеству А.
Рассмотрим несколько примеров.
Ознакомительная версия для принятия решения о покупке книги: Мерзляк, Поляков: Алгебра. Углубленный уровень: 8 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). § 1. Повторение и расширение сведений о множествах. Подмножество.
Урок алгебры в 8 классе по теме «Множества. Элементы множеств» УМК А.Г. Мерзляк
Тема: Множество и его элементы. Урок № 51 13.01.2020
Деятельностная цель: формирование у учащихся умений реализации новых способов действия.
Содержательная цель : расширение понятийной базы за счет включения в нее новых элементов: множество, элементы множества, одноэлементное множество, равные множества, характеристическое свойство, пустое множество.
Предметные: Формировать умение описывать понятие множества, элемента множества, задавать конечные множества, распознавать равные множества.
Личностные: Формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.
1. Мотивация (самоопределение) к учебной деятельности.
Организация уч-ся, проверка готовности к уроку. Просмотр первого слайда презентации.
Учитель: Каким общим словом можно назвать предметы, изображенные на картинках?
Сегодня на уроке мы познакомимся с понятием, которое характеризует общие свойства объектов.
2. Актуализация и фиксирование индивидуального затруднения в пробном действии.
А) Решите уравнения:
3) 5х + 15 = 0 (1 решение)
4) 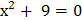
Б) Можете ли вы назвать количество девочек вашего класса, которым исполнилось 13 лет?
А количество мальчиков? Можете ли вы назвать количество учеников вашего класса, которым исполнилось 15 лет?
В) Назовите учеников школы, которые младше 17 лет.
3. Выявление места и причины затруднений.
Скажите, просто или сложно было вам находить ответы на мои вопросы? А всегда ли ответы были односложными?
4. Построение проекта выхода из затруднения (цель, тема, план, сроки, способ, средство).
Сегодня на уроке мы начнем изучение темы, которая называется «Множества и его элементы»
Сформулируйте цели урока….
Чтобы усвоение нового материала было успешным, вы будете работать с учебником 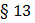
(Читают учебник по цепочке.)
I. Обозначение множеств: А, В, С, М, Н ….
II. Элементы множества:
III. Способы задания множеств: 1) перечислением всех его элементов; 2) указанием характеристического свойства.
IV. Равные множества: множества, состоящие из одних и тех же элементов;
V. Количество элементов множеств: а) бесконечное множества; б) конечные множества
VI. Пустое множество:
5. Реализация построенного проекта
I. Приведите примеры конечного множества; бесконечного множества.
III. Приведите примеры пустого множества.
6. Первичное закрепление с проговариванием во внешней речи.
Работа с учебником : № 426 а) 
№ 428; 1) да; 2) нет; 3) да; 4) нет; 5) нет; 6) да;
7. Самостоятельная работа с самопроверкой по эталону
№ 430 1) 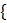
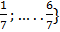

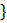
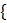
№ 433 1) 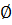
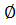
8. Включение в систему знаний повторение.
Решение: 42- 14-16 = 12. Р(зел.)=
9. Рефлексия УД на уроке (Слайд 16)
Домашнее задание: п. 13, № 427, 432
Мы только начинаем знакомиться с множествами. (Слайд 3)
Например, можно говорить о множестве цветов, которые растут на клумбе около нашей школы. Или о множестве точек на плоскости. Элементы множества могут быть любыми!
Говоря о множестве А, мы просто перечисляли его элементы. Иногда это отнимает много времени. Иногда вообще такое перечисление невозможно.
Дополнительные вопросы. Существует ли в этом множестве наибольший элемент? Приведите примеры элементов этого множества, которые меньше 1; 0,1; 0,01; 0,001. Существует ли наименьший элемент этого множества? Будет ли принадлежать этому множеству число 0?
На этом примере показано, что мы можем задать множество, описав самое важное свойство его элементов (оно называется характеристическим свойством множества). По этому свойству можно точно понять, из каких элементов состоит данное множество. Если нам удается это свойство сформулировать, то не нужно тратить время на перечисление элементов множества. Указав множество цветов, растущих на школьной клумбе, мы не обязаны перечислять все цветы. Мы только указали, где они находятся.
Таким образом, множества могут быть заданы по-разному. Самое главное, чтобы было понятно, какие именно элементы принадлежат данному множеству, а какие не принадлежат. Элементы могут быть любые, их порядок не важен. (Слайд 6)
Если два множества состоят из одних и тех же элементов, мы их считаем равными. Пусть множество М состоит из элементов: квадрат, трапеция, пятиугольник, круг, треугольник. Множество Р: круг, квадрат, треугольник, пятиугольник, трапеция. Будут ли множества М и Р равны? Ответ поясните.
Отметим, что здесь мы обсуждаем множество именно как математическое понятие. Но ведь в нашем обычной речи тоже встречается слово «множество»! Важно их не перепутать. «Математическое» множество вовсе не обязано состоять из большого количества элементов. Множество может содержать и всего один элемент. Например, пусть множество D состоит из моей птицы Чир. И даже может быть так, что в множестве вообще нет никаких элементов!
О некоторых множествах трудно сразу сказать, пусты ли они или нет. Например, знаменитая проблема Ферма была решена только в 90-х годах ХХ века: было доказано, что не существует натуральных чисел n, больших двух, при которых уравнение x n +y n =z n имеет целочисленные положительные решения, то есть множество таких n пусто.
Приведите сами примеры различных пустых множеств.
Среди всех множеств выделяют конечные множества и бесконечные. (Слайд 8)
В конечном множестве число его элементов всегда можно выразить определенным числом (иногда, правда, это число не так-то просто найти).
Приведем несколько примеров.
Рассмотрим множество, состоящее из гласных букв. Сколько в нем элементов?
Будет ли это множество равно множеству, состоящему из цифр?
Перед человечеством встали задачи, которые можно решить с помощью существующих компьютеров только теоретически. В реальности на их решение потребуется время, сравнимое со временем существования Вселенной [3].
Математики и другие ученые предлагают ответы на то, как обойти эти барьеры и ищут новые решения.
Бесконечные множества. В них количество элементов выразить конечным числом невозможно.
Примеры бесконечных множеств:
Запишите для каждого числа, принадлежит ли оно множествам N, Z, Q, R.
Мы уже знакомы с понятием «числовые промежутки». Это тоже множества.
Как вы думаете, сколько всего действительных чисел на промежутке (5;8)? Сколько на нем целых чисел? Назовите их.
Аналогичные вопросы можно рассмотреть для промежутков [5;8], [5;8).
Почему нужно было расположить прямую CD параллельно АВ? Укажите прямую, которая пройдет через точку О, но не пересечет дугу. Не забудьте, что мы рассматриваем дугу без концов!
Более трудный вопрос. Можно ли аналогичным образом устроить «переезд» точек для [5; 8], [5; 8)? Замечаем, что «мешают» граничные точки. С теми ребятами, кого заинтересует эта задача, мы обсудим ее на факультативном занятии.
Для всех множеств (и конечных, и бесконечных), мы должны научиться определять, какие элементы принадлежат данному множеству, а какие нет.
Рассмотрим два множества, А и В. Пусть множество А состоит из параллелограмма, трапеции, треугольника, квадрата. Множество В состоит из круга, квадрата, треугольника, пятиугольника, трапеции.
Класс: 8
Презентация к уроку
Множества в школьной математике ведут себя примерно так же, как обитатели леса: мы их почти не видим, но знаем, что они есть.
В классах с углубленным изучением математики основные понятия теории множеств рассматриваются достаточно подробно. Например, в [1] им посвящена глава «Элементы теории множеств». Ученик, изучивший эту главу, сможет лучше ориентироваться в других разделах математики.
Для обычного класса такую подготовку провести трудно, даже если содержание упомянутой главы значительно сократить. Слишком много новых терминов, чисто абстрактных рассуждений и специфической символики. Да и количество часов по программе не позволяет вводить дополнительную тему. Но если ученика математического класса можно сравнить с опытным охотником, который уверенно идет по лесу, то ученику обычного класса нужен хотя бы определенный минимум знаний по теории множеств, чтобы не заблудиться в трех соснах.
В обычных классах множества только изредка упоминаются. Чтобы сильные ученики смогли, тем не менее, овладеть нужными знаниями, возможно, например, изучать элементы теории множеств на факультативных занятиях. Но все-таки по возможности основные сведения должны получить все дети.
Решительный шаг в этом направлении сделан в последнем издании учебника по алгебре для 8 класса [5]. В прежних изданиях в разделе «Квадратные корни» назывались основные числовые множества (натуральные числа, целые, рациональные, действительные). Вводился знак принадлежности. Сейчас к этому добавилось определение подмножества (и знак включения). Говорится о взаимно однозначном соответствии между точками на прямой и действительными числами.
В теме «Неравенства» помимо рассмотрения числовых промежутков введен параграф «Пересечение и объединение множеств». Если раньше данным терминам уделялось немного внимания при рассмотрении промежутков, то теперь ученик сможет более детально ознакомиться с операциями над множествами. С недавних пор появился новый предмет «Теория вероятностей и статистика». Как раз в курсе теории вероятностей для 8 класса [6] при изучении алгебры событий говорится о правиле суммы и произведения, демонстрируются в качестве иллюстраций круги Эйлера. Нам представляется, что если ученик к этому времени будет знать, что такое вообще объединение и пересечение множеств (а не только для числовых множеств), то и в теории вероятностей объединение, пересечение событий этот ученик встретит как своих знакомых.
Но хотелось бы отметить, что само понятие множества в [5]подробно не обсуждается. По-видимому, авторы учебника допускают, что интуитивно ученик понимает это слово, первый раз встречаясь со словами «множество натуральных чисел» и т.д. Практика показывает, что это не так. У детей в первую очередь срабатывает реакция на названия «натуральные», «целые» и т.д. Они стараются их не перепутать, особенно «рациональные», «иррациональные», «действительные». Хотя предварительные сведения об этих числах встречаются уже в 6 классе, все равно для некоторых детей они оказываются трудными: во-первых, сами названия непростые, во-вторых, использование этих названия не так уж часто.
Чтобы понятие множества более органично воспринималось детьми, я посвящала ему отдельный урок в теме «Неравенства». На следующем уроке вводилось определение подмножества, рассматривалось число подмножеств конечного множества. Затем изучались операции над множествами, Эти уроки предшествовали занятиям по теории вероятностей.
В другом классе ученики не такие подготовленные. Им, скажем, сложно было воспринимать даже само слово «множество», потому что они с трудом могли настроиться на то, что это математический термин, а не обычное слово «множество», то есть «много». Поэтому для них я готовила больше простых конкретных примеров.
В презентации я использовала тот образ множества, который предложил Н.Н. Лузин: «Представим прозрачную непроницаемую оболочку, нечто вроде закрытого прозрачного мешка. Предположим, что внутри этой оболочки заключены все элементы данного множества и что, кроме них, внутри оболочки никаких других предметов не находится»[1].
Тем самым мы фиксируем элементы данного множества, а оболочка показывает, что они собраны в одно множество. Когда мы записываем множество с помощью фигурных скобок, именно эти скобки подчеркивают, что данные элементы составляют множество.
Поэтому на слайдах некоторые множества изображены как будто помещенными в прозрачные шары.
В данной статье представлен материал к уроку «Введение понятия множества».
Ключевые слова: «Множество, элемент множества, пустое множество, конечные и бесконечные множества«.
Понятия теории множеств отражают наиболее общие свойства математических объектов.
Мы только начинаем знакомиться с множествами.
Например, можно говорить о множестве цветов, которые растут на клумбе около нашей школы. Или о множестве точек на плоскости. Элементы множества могут быть любыми!
Говоря о множестве А, мы просто перечисляли его элементы. Иногда это отнимает много времени. Иногда вообще такое перечисление невозможно.
Дополнительные вопросы. Существует ли в этом множестве наибольший элемент? Приведите примеры элементов этого множества, которые меньше 1; 0,1; 0,01; 0,001. Существует ли наименьший элемент этого множества? Будет ли принадлежать этому множеству число 0?
На этом примере показано, что мы можем задать множество, описав самое важное свойство его элементов (оно называется характеристическим свойством множества). По этому свойству можно точно понять, из каких элементов состоит данное множество. Если нам удается это свойство сформулировать, то не нужно тратить время на перечисление элементов множества. Указав множество цветов, растущих на школьной клумбе, мы не обязаны перечислять все цветы. Мы только указали, где они находятся.
Таким образом, множества могут быть заданы по-разному. Самое главное, чтобы было понятно, какие именно элементы принадлежат данному множеству, а какие не принадлежат. Элементы могут быть любые, их порядок не важен.
Если два множества состоят из одних и тех же элементов, мы их считаем равными. Пусть множество М состоит из элементов: квадрат, трапеция, пятиугольник, круг, треугольник. Множество Р: круг, квадрат, треугольник, пятиугольник, трапеция. Будут ли множества М и Р равны? Ответ поясните.
Отметим, что здесь мы обсуждаем множество именно как математическое понятие. Но ведь в нашем обычной речи тоже встречается слово «множество»! Важно их не перепутать. «Математическое» множество вовсе не обязано состоять из большого количества элементов. Множество может содержать и всего один элемент. Например, пусть множество D состоит из моей птицы Чир. И даже может быть так, что в множестве вообще нет никаких элементов!
О некоторых множествах трудно сразу сказать, пусты ли они или нет. Например, знаменитая проблема Ферма была решена только в 90-х годах ХХ века: было доказано, что не существует натуральных чисел n, больших двух, при которых уравнение x n +y n =z n имеет целочисленные положительные решения, то есть множество таких n пусто.
Приведите сами примеры различных пустых множеств.
Среди всех множеств выделяют конечные множества и бесконечные.
В конечном множестве число его элементов всегда можно выразить определенным числом (иногда, правда, это число не так-то просто найти).
Рассмотрим множество, состоящее из гласных букв. Сколько в нем элементов?
Будет ли это множество равно множеству, состоящему из цифр?
Перед человечеством встали задачи, которые можно решить с помощью существующих компьютеров только теоретически. В реальности на их решение потребуется время, сравнимое со временем существования Вселенной [3].
Математики и другие ученые предлагают ответы на то, как обойти эти барьеры и ищут новые решения.
Бесконечные множества. В них количество элементов выразить конечным числом невозможно.
Запишите для каждого числа, принадлежит ли оно множествам N, Z, Q, R.
Мы уже знакомы с понятием «числовые промежутки». Это тоже множества.
Как вы думаете, сколько всего действительных чисел на промежутке (5;8)? Сколько на нем целых чисел? Назовите их.
Аналогичные вопросы можно рассмотреть для промежутков [5;8], [5;8).
Почему нужно было расположить прямую CD параллельно АВ? Укажите прямую, которая пройдет через точку О, но не пересечет дугу. Не забудьте, что мы рассматриваем дугу без концов!
Более трудный вопрос. Можно ли аналогичным образом устроить «переезд» точек для [5; 8], [5; 8)? Замечаем, что «мешают» граничные точки. С теми ребятами, кого заинтересует эта задача, мы обсудим ее на факультативном занятии.
Для всех множеств (и конечных, и бесконечных), мы должны научиться определять, какие элементы принадлежат данному множеству, а какие нет.