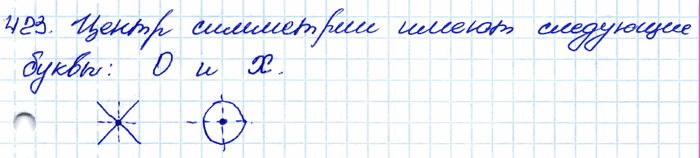Докажите что параллелограмм у которого углы равны а диагонали перпендикулярны является квадратом
Доказать, что параллелограмм, у которого все углы равны, а диагонали перпендикулярны, вляется квадратом?
Доказать, что параллелограмм, у которого все углы равны, а диагонали перпендикулярны, вляется квадратом.
Ну как вариант, не уверен в правильности.
У прямоугольника диагонали равны точкой пересечения делятся пополам то есть ао = ос = во = од, в итоге прямоугольник разобьётся на 4 треугольника аов, вос, сод, аод.
Так как диагонали перпендикулярны то это будут прямоугольные треугольники, у которых катеты будут равны(катетами будут половинки от диаганалей).
Так как катеты равны, то и гипотенузы равны, а гипотенузами будут являться стороны этого прямоугольника, а если у прямоугольника стороны равны, то это квадрат.
Какие из следующих утверждений являются неверными : 1)если два угла одного треугольника равны двум углам другого треугольника, то равны и третьи углы ; 2)если диагонали параллелограмма перпендикулярны?
Какие из следующих утверждений являются неверными : 1)если два угла одного треугольника равны двум углам другого треугольника, то равны и третьи углы ; 2)если диагонали параллелограмма перпендикулярны, то это квадрат ; 3)существует трапеция, все стороны которой имеют равные длины.
Какие из этих утверждений являются неверными?
Какие из этих утверждений являются неверными?
1) Если два угла одного треугольника равны двум углам другого треугольника, то равны и третьи углы 2)Если диагонали параллелограмма перпендикулярны, то это квадрат.
3)Существует трапеция, все стороны которой имеют разные длины.
Докажите, что параллелограмм, у которого стороны равны и диагонали равны является квадратом?
Докажите, что параллелограмм, у которого стороны равны и диагонали равны является квадратом.
Какое из следующих утверждений верно?
Какое из следующих утверждений верно.
В прямоугольнике АBCD диагонали перпендикулярны?
В прямоугольнике АBCD диагонали перпендикулярны.
Доказать что этот прямоугольник квадрат.
1)верно ли что существует ромб не являющийся параллелограммом 2)три угла параллелограмма равны определите вид параллелограмма 3)найдите угол между диагональю и стороной параллелограмма диагонали котор?
1)верно ли что существует ромб не являющийся параллелограммом 2)три угла параллелограмма равны определите вид параллелограмма 3)найдите угол между диагональю и стороной параллелограмма диагонали которого взаимно перпендикулярны и равны.
В параллелограмме диагонали взаимно перпендикулярны?
В параллелограмме диагонали взаимно перпендикулярны.
Можно ли утверждать, что такой четырех угольник является квадратом?
Немного хаотично, но думаю разберетесь.
Держи) Решение задачи на фото).
Нет наверное или да, с какой стороны посмотреть.
Решение в приложении.
Квадрат, его свойства и признаки.
Квадрат, его свойства и признаки.
Определение. Квадратом называется прямоугольник, у которого все стороны равны.
Для квадрата можно ввести несколько определений. Самое ёмкое мы уже привели. Но можно определить квадрат следующим образом:
Квадратом называется четырёхугольник, у которого все стороны равны, а углы прямые.
Квадратом называется параллелограмм, у которого все стороны и углы равны.
Квадратом называется ромб, у которого все углы прямые.
Поскольку квадрат является и параллелограммом, и прямоугольником, и ромбом, то он обладает теми же свойствами, что и все перечисленные четырёхугольники.
У квадрата диагонали пересекаются и точкой пересечения делятся пополам.
У квадрата диагонали взаимно перпендикулярны.
У квадрата диагонали являются биссектрисами его углов.
У квадрата диагонали равны.
У квадрата стороны являются высотами.
Каждая диагональ квадрата делит его на равные прямоугольные треугольники.
Теперь определим признаки квадрата.
ТЕОРЕМА ( I признак). Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Так как – прямоугольник, то у него противолежащие стороны равны.
– квадрат (по определению), ч.т.д.
ТЕОРЕМА ( II признак). Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
по свойству диагоналей прямоугольника, значит, – медиана (по опред-нию).
ТЕОРЕМА ( III признак). Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
ТЕОРЕМА ( IV признак). Если в ромбе диагонали равны, то этот ромб является квадратом.
ТЕОРЕМА ( V признак). Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
ТЕОРЕМА ( VI признак). Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
2. Так как , то параллелограмм является квадратом (по V признаку квадрата), ч.т.д.
ТЕОРЕМА ( VII признак). Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
1. Так как , то четырёхугольник является ромбом (по V признаку ромба).
Если в прямоугольнике две его смежные стороны равны, то он является квадратом.
Если в прямоугольнике диагонали перпендикулярны, то этот прямоугольник является квадратом.
Если в прямоугольнике одна из диагоналей является биссектрисой его угла, то такой прямоугольник является квадратом.
Если в ромбе диагонали равны, то этот ромб является квадратом.
Если в параллелограмме диагонали перпендикулярны и равны, то такой параллелограмм является квадратом.
Если в четырёхугольнике диагонали равны, взаимно перпендикулярны и точкой пересечения делятся пополам, то такой четырёхугольник является квадратом.
Если в четырёхугольнике все стороны равны и среди внутренних углов есть один прямой угол, то такой четырёхугольник является квадратом.
В четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что отрезки, соединяющие середины противоположных сторон, равны.
В равнобедренный прямоугольный треугольник, каждый катет которого равен см, вписан квадрат, имеющий с ним один общий угол. Найдите периметр квадрата.
В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Определите сторону квадрата, если известно, что гипотенуза равна 30 дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них втрое больше другой и что диагональ квадрата равна дм.
В квадрат вписан прямоугольник так, что на каждой стороне квадрата находится одна вершина прямоугольника и стороны прямоугольника параллельны диагоналям квадрата. Определите стороны этого прямоугольника, зная, что одна из них вдвое больше другой и что диагональ квадрата равна см.
Через вершины квадрата проведены прямые, параллельные его диагоналям. Определите вид образованного ими четырёхугольника и вычислите его периметр, если диагональ квадрата равна см.
Найдите периметр квадрата по данным на рисунке.
Докажите, что параллелограмм у которого стороны и диагонали равны является квадратом помогите пожалуйста?
Докажите, что параллелограмм у которого стороны и диагонали равны является квадратом помогите пожалуйста!
По признаку прямоугольника, который звучит : Если в параллелограмме
Мы получили что данный параллелограмм является прямоугольником и все стороны равны = > ; по определению квадрата(Квадратом называется прямоугольник, у которого все стороны равны) имеем, что данный параллелограмм(у которого все стороны равны и диагонали равны) является квадратом.
Докажите что если в параллелограмме диагонали равны то параллелограмм является прямоугольником?
Докажите что если в параллелограмме диагонали равны то параллелограмм является прямоугольником.
Докажите что если в параллелограмме диагонали равны то параллелограм является прямоугольником?
Докажите что если в параллелограмме диагонали равны то параллелограм является прямоугольником.
Привет помогите пожалуйста с задачами?
Привет помогите пожалуйста с задачами!
ПОМОГИТЕ ПОЖАЛУЙСТА БУДУ ОЧЕНЬ БЛАГОДАРЕН?
ПОМОГИТЕ ПОЖАЛУЙСТА БУДУ ОЧЕНЬ БЛАГОДАРЕН!
Докажите, что параллелограмм у которого стороны и диагонали равны является квадратом.
В параллелограмме ABCD диагонали равны?
В параллелограмме ABCD диагонали равны.
Докажите что ABCD является прямоугольником.
Докажите, что параллелограмм, у которого стороны равны и диагонали равны является квадратом?
Докажите, что параллелограмм, у которого стороны равны и диагонали равны является квадратом.
Докажите, что если у ромба диагонали равны, то он является квадратом?
Докажите, что если у ромба диагонали равны, то он является квадратом.
Докажите, что параллелограмм является прямоугольником?
Докажите, что параллелограмм является прямоугольником.
Если диагонали образуют равные углы с одной из его сторон.
Немного хаотично, но думаю разберетесь.
Держи) Решение задачи на фото).
Нет наверное или да, с какой стороны посмотреть.
Решение в приложении.
Геометрия 8 класс Атанасян Задачи 399-423
Упражнения 399 — 423 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 3. Прямоугольник, ромб, квадрат
Задачи №№ 399 — 423:
Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
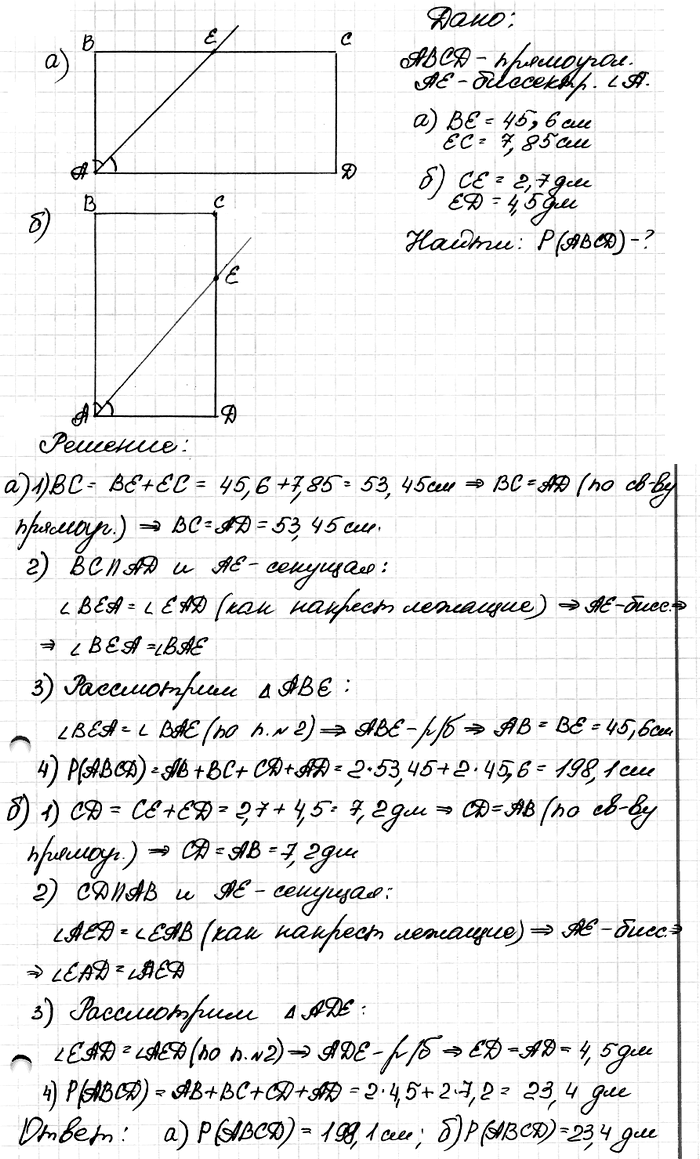
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.
Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.
Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.
Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.
Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.
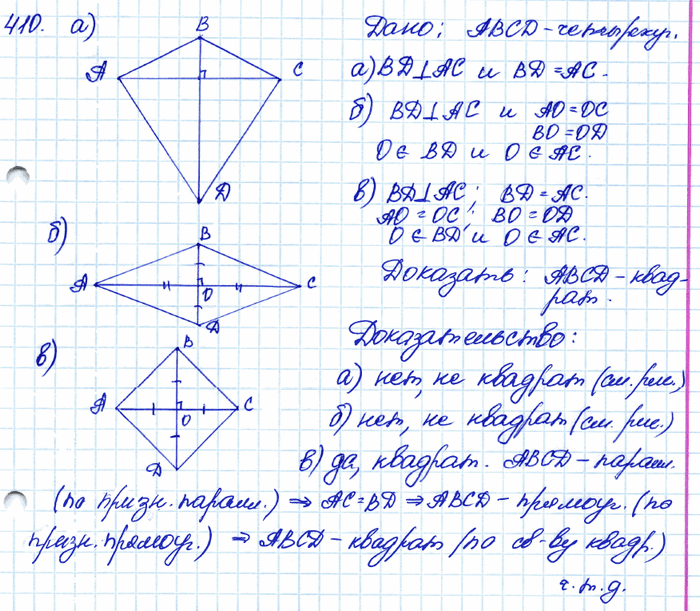
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.
Задача № 412. Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.
Задача № 413. □ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.
Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.
Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Задача № 417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.
Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.