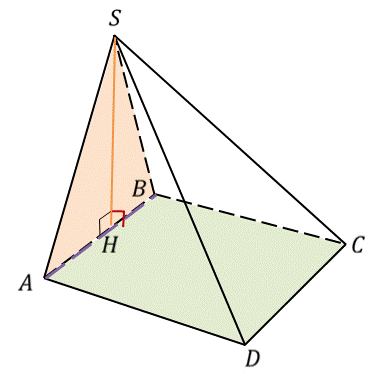
Докажите что плоскость перпендикулярная к прямой по которой пересекаются две данные плоскости

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №11. Перпендикулярность плоскостей

Перечень вопросов, рассматриваемых в теме.

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Перпендикуляры к ребру двугранного угла образуют линейный угол двугранного угла. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Если угол между пересекающимися плоскостями равен 90 градусом, то плоскости перпендикулярны.

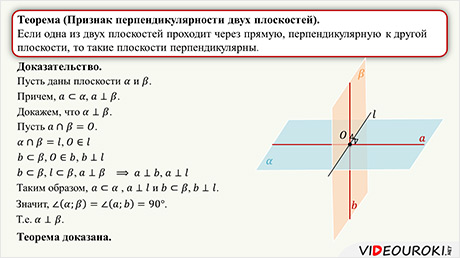
Признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Следствие из признака перпендикулярности плоскостей: Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Прямоугольный параллелепипед – фигура, у которой все боковые ребра перпендикулярны основанию.

Атанасян Л.С., Бутузов В.Ф. Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.

Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения

Двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей в виде прямой а, не принадлежащими одной плоскости. Полуплоскости, образующие двугранный угол, называются его гранями. Прямая а, которая является общей границей полуплоскостей, называется ребром двугранного угла (рис. 1а и 1б).

Двугранный угол с ребром CD, на разных гранях которого отмечены точки A и B называют двугранным углом CABD.

Перпендикуляры к ребру AO и BO образуют линейный угол двугранного угла AOB (рис. 1в). Так как луч ОА перпендикулярен прямой CD и луч OB перпендикулярен прямой CD, то плоскость АОВ перпендикулярна к прямой CD. Таким образом, плоскость линейного угла перпендикулярна к ребру двугранного угла. Двугранный угол имеет бесконечное множество линейных углов

Градусной мерой двугранного угла называется градусная мера его линейного угла. Так же как и плоские углы, двугранные углы могут быть прямыми, острыми и тупыми.

Все линейные углы двугранного угла равны друг другу.

Рассмотрим два линейных угла АОВ и А₁О₁В₁ (рис. 1г). Лучи ОА и О₁А₁, лежат в одной грани и перпендикулярны к прямой ОО₁, поэтому они сонаправлены. Точно так же сонаправлены лучи OB и O₁B₁. Поэтому углы АОВ и А₁О₁В₁ равны как углы с сонаправленными сторонами.

Две пересекающиеся плоскости образуют четыре двугранных угла с общим ребром.

Если один из этих двугранных углов равен фи, то другие три угла равны соответственно 180 градусов минус фи, фи и 180 градусов минус фи (рис. 2 а). В частности, если один из углов прямой, то и остальные три угла прямые. Если угол между пересекающимися плоскостями равен 90 градусом, будем называть такие плоскости перпендикулярными (рис. 2б).

Для доказательства теоремы рассмотрим плоскости альфа и бетта такие (рис. 3), что плоскость альфа проходит через прямую АВ, перпендикулярную к плоскости бетта и пересекающуюся с ней в точке А. Докажем, что плоскости альфа и бетта перпендикулярны. Плоскости альфа и бетта пересекаются по некоторой прямой АС. При этом прямая АВ перпендикулярна прямой АС, так как по условию прямая АВ перпендикулярна плоскости бетта, это означает, что прямая АВ перпендикулярна к любой прямой, лежащей в плоскости бетта.

Проведем в плоскости бетта прямую AD, перпендикулярную к прямой АС. Тогда угол BAD — линейный угол двугранного угла, образованного при пересечении плоскостей альфа и бетта. Но угол BAD равен 90 градусов так как прямая АВ перпендикулярна плоскости бетта. Следовательно, угол между плоскостями альфа и бетта равен 90 градусов. Что и требовалось доказать.

Из этой теоремы вытекает важное следствие:

Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

На рисунке 4 представлен прямоугольный параллелепипед. У этой фигуры все боковые ребра перпендикулярны основанию.

Его основаниями служат прямоугольники ABCD и A₁B₁C₁D₁, а боковые ребра АА₁,BB₁,CC₁ и DD₁ перпендикулярны к основаниям. Отсюда следует, что ребро АА₁ перпендикулярно к ребру АВ, т. е. боковая грань АА₁В₁В является прямоугольником. То же самое можно сказать и об остальных боковых гранях.

Таким образом, прямоугольный параллелепипед обладает следующими свойствами:

1) В прямоугольном параллелепипеде все шесть граней — прямоугольники.

2) Все двугранные углы прямоугольного параллелепипеда — прямые.

3) Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Измерениями прямоугольного параллелепипеда называются длины трех ребер, имеющих общую вершину.

Докажем последнее свойство.

Так как ребро СС₁ перпендикулярно к основанию ABCD, то угол АСС₁, прямой. Из прямоугольного треугольника АСС₁, по теореме Пифагора получаем

Следствием из этого свойства является то, что диагонали прямоугольного параллелепипеда равны.

Стоит отметить, что если у прямоугольного параллелепипеда все три измерения равны, то он называется, а все его грани являются равными друг другу квадратами.

Примеры и разбор решения заданий тренировочного модуля

Пример 1. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ (рис. 5) боковая грань DD₁C₁C – квадрат, DC равно 4 см, BD₁ равно 6 см. Найдите BC и докажите, что плоскости BCD₁ и DC₁ B₁ взаимно перпендикулярны.

Сначала найдем BC. Воспользуемся тем свойством прямоугольного параллелепипеда, что квадрат его диагонали равен сумме квадратов трех его измерений.

Тогда диагональ BD₁ в квадрате равна AD в квадрате плюс DD₁ в квадрате плюс DC в квадрате. BD₁ – известно из условия, DD₁ и DC – стороны квадрата и тоже известны из условия, тогда отсюда мы можем выразить ребро AD, которое ребру BC.Отсюда находим, что BC равно 2 сантиметрам.

Для доказательства перпендикулярности плоскостей BCD₁ и DC₁ B₁ воспользуемся признаком перпендикулярности плоскостей. Этот признак звучит следующим образом: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Заметим, что плоскость BCD₁ проходит через диагональ грани DD₁ C₁C – CD₁. Эта диагональ перпендикулярна плоскости DC₁ B₁ в соответствии с признаком перпендикулярности прямой и плоскости, так как CD₁ перпендикулярна второй диагонали квадрата – C₁D и перпендикулярна ребру прямоугольного параллелепипеда C₁ B₁. Что и требовалось доказать.

Тестовый вопрос №2. В прямом двугранном угле дана точка A. Расстояния от точки A до граней угла: AA₁=6 см и AB₁=8 см. Определите расстояние от точки A до ребра двухгранного угла.

Отрезки AA₁ и AB₁ перпендикулярны граням двугранного угла, поэтому AA₁BB₁ – прямоугольник. Искомое расстояние – диагональ этого прямоугольника, которую найдем с помощью теоремы Пифагора: сантиметров.

Тестовый вопрос №10. В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ длины рёбер: AB = 2, BC=3, AA₁ = 4. Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки A, B и C_​1​​.

Решение. Нарисуем рисунок.

В рассматриваемом прямоугольном параллелепипеде проведем отрезок BC_​1​​. Затем построим плоскость на прямых BC_​1​​ и AB. Так как плоскости прямоугольного параллелепипеда AA₁D₁D и BB₁C₁C параллельны, поэтому искомым сечением является прямоугольник ABC₁D₁.

Источник

Признак перпендикулярности двух плоскостей

Урок 23. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Признак перпендикулярности двух плоскостей»

· рассмотрим перпендикулярные плоскости;

· сформулируем и докажем признак перпендикулярности двух плоскостей.

Для начала давайте вспомним определение двугранного угла. Итак, двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости. Причем, полуплоскости, образующие двугранный угол, называются его гранями. А прямая а – общая граница полуплоскостей – называется ребром двугранного угла.

Введем понятие угла между плоскостями.

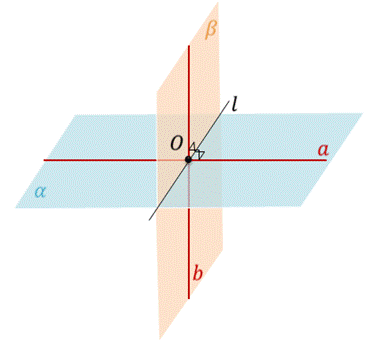
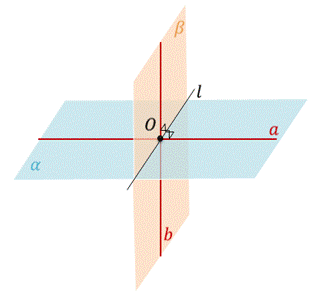
Определение. Углом между пересекающимися плоскостями называется угол между прямыми, проведенными в плоскостях перпендикулярно их линии пересечения через некоторую точку.

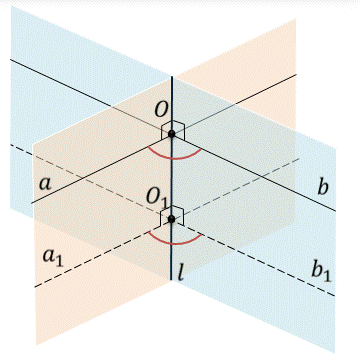
Заметим, что определение угла между плоскостями не зависит от выбора прямых а и b, проведенных в плоскостях и перпендикулярных их линии пересечения. Действительно, если в данных плоскостях провести какие-нибудь другие прямые a₁ и b₁ перпендикулярно их линии пересечения _l через точку O₁, то прямая а будет параллельна прямой a₁ и прямая b будет параллельна прямой b₁. А следовательно, угол между прямыми а и b равен углу между прямыми a₁ и b₁.

Если плоскости параллельны, то угол между ними считается равным 0°. Угол между плоскостями α и β обозначают следующим образом .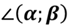

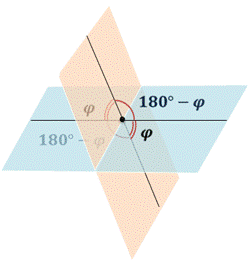
Если в пространстве пересекаются две плоскости, то они образуют четыре двугранных угла с общим ребром (аналогично как при пересечении двух прямых получаются четыре угла).

Если известен один из этих двугранных углов, то можно найти и другие три двугранных угла. Т.е. если один из этих двугранных углов равен φ, то другие три угла равны соответственно 180°-φ, φ и 180°-φ.

Если при пересечении плоскостей один из углов прямой (т.е. фи равен 90°), то и остальные три угла прямые. Такие плоскости называют перпендикулярными.

Если φ – тот из четырех углов, который не превосходит каждого из остальных, то говорят, что угол между пересекающимися плоскостями равен φ. Очевидно, что угол φ лежит в промежутке от 0° до 90°.

Определение. Две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен девяносто градусов.

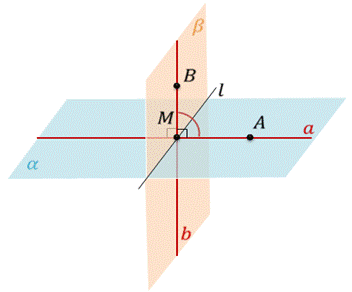
Пусть есть две плоскости α и β, которые пересекаются по прямой l. Отметим произвольную точку М на прямой l. Затем через точку М проведем две прямые а и b перпендикулярные к прямой l в плоскости α и в плоскости β соответственно. На построенных прямых отметим точки А и B соответственно. Обратите внимание, мы получили угол AMB. Угол AMB – это линейный угол двугранного угла. Если угол AMB равен 90°, то плоскости α и β называются перпендикулярными.

Действительно, прямая b перпендикулярна прямой l по построению. Прямая b перпендикулярна прямой а, так как угол между плоскостями α и β равен 90°. Следовательно, прямая b перпендикулярна двум пересекающимся прямым а и l из плоскости α. Значит, прямая b перпендикулярна плоскости α.

Аналогично можно показать, что прямая а перпендикулярна плоскости β. Прямая а перпендикулярна прямой l по построению. Прямая а перпендикулярна прямой b, так как угол между плоскостями α и β равен 90°. Отсюда следует, что прямая а перпендикулярна двум пересекающимся прямым b и l из плоскости β. Значит, прямая а перпендикулярна плоскости β.

Примером взаимно перпендикулярных плоскостей служат плоскости стены и пола комнаты.

Ясно, что все четыре двугранных угла, образованные взаимно перпендикулярными плоскостями, прямые.

Теорема. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Пусть даны плоскости α и β. Причем такие, что плоскость альфа проходит через прямую а, перпендикулярную к плоскости β. Докажем, что плоскости α и β перпендикулярны.

Пусть точка О – точка пересечения прямой а с плоскостью β. Точка О – общая точка плоскостей α и β, следовательно, данные плоскости пересекаются по прямой l, проходящей через точку О.

В плоскости β через точку О проведем прямую b, перпендикулярную прямой l.

Прямые b и l лежат в плоскости β и по условию прямая а перпендикулярна плоскости β. Следовательно, прямая а перпендикулярна прямой b и прямая а перпендикулярна прямой l. Таким образом, получаем, что прямая а лежит в плоскости α, перпендикулярна прямой l и прямая b лежит в плоскости β перпендикулярно прямой l. Значит, угол между плоскостями α и β равен углу между прямыми а и b и равен 90°. Т.е. получили, что плоскости α и β перпендикулярны.

Следствие. Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

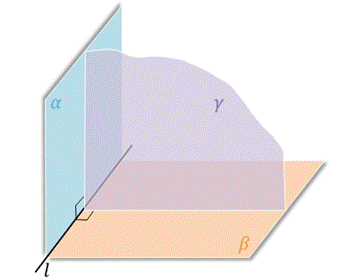
Доказательство. Пусть даны две перпендикулярные плоскости α и β, которые пересекаются по прямой l. И дана плоскость γ, которая перпендикулярна линии пересечения плоскостей α и β, т.е. перпендикулярна прямой l. Докажем, что каждая из плоскостей α и β перпендикулярна плоскости γ.

Прямая l перпендикулярна плоскости γ, а плоскость α проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости α и γ перпендикулярны.

Прямая l перпендикулярна плоскости γ, а плоскость β проходит через прямую l. Значит, по признаку перпендикулярности плоскостей, плоскости β и γ перпендикулярны.

Таким образом, получаем, что плоскость α перпендикулярна плоскости γ и плоскость β перпендикулярна плоскости γ.

Что и требовалось доказать.

Второе следствие. Прямая, проведенная в одной из двух перпендикулярных плоскостей перпендикулярно прямой, по которой они пересекаются, перпендикулярна другой плоскости.

Доказательство. Пусть даны две перпендикулярные плоскости α и β, которые пересекаются по прямой l. И дана прямая b, которая лежит в плоскости β и перпендикулярна линии пересечения плоскостей α и β, т.е. перпендикулярна прямой l. Докажем, что прямая b перпендикулярна плоскости α.

Обозначим буквой О точку пересечения прямой b с прямой l. Затем проведем в плоскости α через точку О прямую а перпендикулярно прямой l. Прямые а и b перпендикулярны прямой l, по которой пересекаются плоскости α и β. Следовательно, угол между прямыми а и b равен углу между плоскостями α и β. Значит, равен 90°.

Таким образом, прямая b перпендикулярна пересекающимся прямым а и l плоскости α. Следовательно, прямая b перпендикулярна плоскости α.

Что и требовалось доказать.

Что и требовалось доказать.

Подведем итоги урока. На этом уроке мы узнали, что две пересекающиеся плоскости называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен девяносто градусов. Сформулировали и доказали признак перпендикулярности двух плоскостей. А также вывели и доказали некоторые следствия.

Источник

Перпендикулярность плоскостей

Перпендикулярность плоскостей — это если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна к этой плоскости.

Определение: две плоскости называются взаимно перпендикулярными, если они образуют прямые двугранные углы.

Содержание:

Понятие перпендикулярности плоскостей

Две пересекающиеся плоскости образуют двугранные углы. Если эти двугранные углы прямые, то говорят, что плоскости взаимно перпендикулярны.

Определение. Две пересекающиеся плоскости называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых двугранных угла.

Можно доказать следующее свойство перпендикулярных плоскостей.

Теорема 4. Прямая, лежащая в одной из двух взаимно перпендикулярных плоскостей и перпендикулярная их линии пересечения, перпендикулярна другой плоскости. Верно и обратное свойство.

Теорема 5. Прямая, имеющая общую точку с одной из двух взаимно перпендикулярных плоскостей и перпендикулярная другой плоскости, лежит в первой из них.

Имеет место признак перпендикулярности двух плоскостей.

Теорема 6. Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то такие плоскости перпендикулярны.

Следствие. Плоскость, перпендикулярная прямой, по которой пересекаются две данные плоскости, перпендикулярна каждой из этих плоскостей.

На рисунке 2.391 плоскость перпендикулярна прямой , по которой пересекаются две плоскости и . Значит, согласно следствию, плоскость будет перпендикулярна плоскостям и .

С помощью свойств перпендикулярных плоскостей можно доказать еще один признак перпендикулярности прямой и плоскости.

Теорема 7. Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.

Пример:

Из условия теоремы имеем:

1. Прямая АВ принадлежит плоскости .

2. , АВ пересекает в точке В.

3. (требуется доказать).

4. Плоскости и имеют общую точку В, а значит, пересекаются по некоторой прямой CD (1, 2, аксиома 5) (рис. 2.392).

Нам нужно доказать перпендикулярность плоскостей и . Как это можно сделать? Ответ однозначный — только через рассмотрение двугранных углов и градусных мер их линейных углов (они должны быть прямые). У нас на рисунке нет нужных нам линейных углов. Это подсказывает следующее построение.

5. Проведем в плоскости прямую MN, перпендикулярную CD и проходящую через точку B (построение) (рис. 2.393).

6. , значит, — линейный угол двугранного угла с ребром CD (2, 5, определение линейного угла двугранного угла).

7. (2, 6).

8. (1, 7).

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник