Докажите что предел произведения двух сходящихся последовательностей равен произведению их пределов

Свойства сходящихся последовательностей

Лекция 2. Сходящиеся последовательности. Монотонные последовательности. Основные теоремы.

Свойства сходящихся последовательностей

Теорема 1

Сходящаяся последовательность имеет только один предел.

Пусть a и b – пределы сходящейся последовательности . Используя формулу (2) можно записать и , где , — бесконечно малые последовательности. Вычитая, получим Так как, все элементы последовательности имеют одно и тоже значение b-a, то по теореме 5 (см. ранее) b-a=0 и b=a. Теорема доказана.

Теорема 2

Сходящаяся последовательность ограничена.

Пусть последовательность сходящаяся и а – ее предел. Имеет место формула , — бесконечно малая последовательность. Так как бесконечно малая последовательность — ограничена (теорема 3), то справедливо . Поэтому для всех номеров n, что и означает ограниченность последовательности .

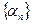
Ограниченная последовательность может быть и не сходящейся.

Например

Теорема 3

Сумма сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей и .

Пусть и . Тогда и , соответственно . Таким образом, последовательность — бесконечно малая, и поэтому последовательность сходится и имеет своим пределом a+b.

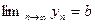
Теорема 4

Разность сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен разности пределов последовательностей и . Доказательство аналогичное.

Теорема 5

Произведение сходящихся последовательностей и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей и .

Пусть и . Тогда и , соответственно

Лемма

Если последовательность сходится, то есть , то, начиная с некоторого номера, определена последовательность , которая является ограниченной.

Пусть . Так как . Пусть N – номер, соответствующий этому , начиная с которого выполняется неравенство . Из этого неравенства следует, что при выполняется неравенство . Действительно

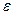
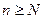
Поэтому, при 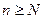имеем . Следовательно, начиная с этого номера N, можно рассматривать последовательность , и эта последовательность ограничена. Лемма доказана.

Теорема 6

Частное двух сходящихся последовательностей и при условии, что предел последовательности отличен от 0, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и .

Из леммы следует, что, начиная с некоторого номера N элементы не равны 0 и последовательность — ограничена. Начиная с этого номера, рассмотрим последовательность . Пусть и .

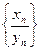
Докажем, что — бесконечно малая последовательность. Так как и ,

то . Так как — ограничена, а последовательность — бесконечно малая, то последовательность — бесконечно малая, то есть . Теорема доказана.

Источник

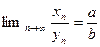
Предел последовательности. Свойства сходящихся последовательностей

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Отсюда следует, что добавление к последовательности конечного числа элементов или исключение из нее конечного числа элементов не влияет на ее сходимость и значение ее предела, изменяется лишь номер, начиная с которого все элементы последовательности попадают в выбранную ^-окрестность точки ft.

Пример 6.3. а:

Убедимся, что для (6.5) В силу очевидного неравенства 2+ (-!)» 3 п п примем N = [3/е]. Тогда при произвольном е > 0 для п > [3/е] будет выполнено условие в (6.7). в.

Предел последовательности

Свойства сходящихся последовательностей. В самом деле, при любом е > 0. Поэтому в (6.7) в качестве N можно выбрать любое натуральное число. Пример в.4. Проверим, что при а > 1 При предположим, что По определению логарифма, loga ап = п.

Отсюда Следствие 6.1. Сходящаяся последовательность, элементы которой знакопостоянны, не может иметь предел другого знака. В самом деле, если бы предел последовательности имел иной знак, то, согласно теореме 6.3, начиная с некоторого номера ее элементы приняли бы знак предела, что противоречит исходному условию. Пусть даны две последовательности <х„>и <уп>. Их суммой, произведением и частным называют последовательности <хп + Уп>, <х„у„>и <хп/у„>, а обратной к <у„>— последовательность <1>, причем последовательности <хп/уп>и <1 >определены лишь при условии уп ф 0 Vn € N. Ясно, что Теорема 6.4.

Если последовательности <хп>и <у„>сходятся соответственно к пределам а и 6, то Обозначим и выберем произвольное € > 0. Тогда: 1) для сходящихся последовательностей, по определению 6.3, что, согласно определению 6.3 предела последовательности, доказывает (6.10); 2) воспользуемся тождеством и с учетом (1.4) запишем по теореме 6.2 об ограниченности сходящейся последовательности и определению 6.2 ограниченной последовательности, для сходящихся последовательностей, согласно определению 6.3.

Ясно, что (6.10) и (6.11) нетрудно обобщить на любое конечное число слагаемых или сомножителей, если в их качестве •взять сходящиеся последовательности. Следствие в.2. При вычислении предела сходящейся последовательности один и тот же постоянный сомножитель в ее элементах можно выносить за символ предела.

Возможно вам будут полезны данные страницы:

Выполним предварительно тождественные преобразования а из (6.19) искомый предел равен 1/5. Пример 6.8. Введенные при доказательстве теоремы 6.4 величины Дяп = |а-яп| и Луп = |6-у„| можно рассматривать как абсолютные погрешности приближенных значений хп и уп соответственно величин а и Ь. Тогда полученные в ходе доказательства теоремы соотношения, приближенно заменяя в них а на |хп| и |6| на |уп|, можно использовать для оценки погрешностей, возникающих при суммировании, умножении, обращении и делении приближенных значений, а именно:

Наибольшая возможная (максимальная) погрешность алгебраической суммы равна сумме погрешностей слагаемых, т.е. Бели в качестве погрешностей слагаемых рассматривать ошибки округления, то значение Дтах(яп + Уп) наиболее чувствительно к погрешности наименее точного слагаемого. Поэтому, чтобы избежать лцшних вычислений, не следует сохранять в более точном слагаемом лишние значащие цифры.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Сходящиеся последовательности

Последовательность, у которой существует предел, называется сходящейся. Последовательность не являющаяся сходящейся называется расходящейся.

В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.

Можно, также, дать еще одно определение сходящейся последовательности: Последовательность называется сходящейся, если существует такое число а, что для любого положительного числа e можно указать номер N такой, что при n³ N все элементы x n этой последовательности удовлетворяют неравенству:

Некоторые свойства сходящихся последовательностей:

ТЕОРЕМА: Сходящаяся последовательность имеет только один предел.

ТЕОРЕМА: Сходящаяся последовательность ограничена.

Доказательство: Пусть — сходящаяся последовательность и а – ее предел. Представим ее в следующем виде:

ТЕОРЕМА: Сумма сходящихся последовательностей <х n >и есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей <х n >и .

Доказательство: Пусть а и b – соответственно пределы последовательностей <х n >и . Тогда:

ТЕОРЕМА: Разность сходящихся последовательностей <х n >и есть сходящаяся последовательность, предел которой равен разности пределов последовательностей <х n >и .

Доказательство: Пусть а и b – соответственно пределы последовательностей <х n >и .Тогда:

ТЕОРЕМА: Произведение сходящихся последовательностей <х n >и есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей <х n >и .

ЛЕММА: Если последовательность сходится и имеет отличный от ноля предел b, то, начиная с некоторого номера, определена последовательность , которая является ограниченной.

ТЕОРЕМА: Частное двух сходящихся последовательностей и при условии, что предел отличен от ноля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей и .

.

Так как последовательность ограничена, а последовательность бесконечно мала, то последовательность бесконечно малая. Теорема доказана.

Итак, теперь можно сказать, что арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.

ТЕОРЕМА: Если элементы сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравентству x n³ b (x n£ b), то и предел а этой последовательности удовлетворяет неравенству а³ b (a£ b).

Элементы сходящейся последовательности могут удовлетворять строгому неравенству x n >b, однако при этом предел а может оказаться равным b. Например, если x n =1/n, то x n >0, однако .

.

.

Следствие 2: Если все элементы сходящейся последовательности находятся на сегменте [a,b], то и ее предел с также находится на этом сегменте.

Это выполняется, так как а£ x n£ b, то a£ c£ b.

Итак, мы показали неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.

, и того, что .

(m, n = 1, 2, 3, … ),

,…

должна либо расходиться к , причем предел этой последовательности будет равен ее нижней грани.

,

тогда существует конечный предел

,

(n = 1, 2, 3, … ).

(*)

сходится, ибо в силу неравенства (*) он мажорируется сходящимся рядом:

запишем целое число n по двоичной системе:

.

Применяя теорему (1) для данных:

s 0 =0, s 1 =, s m-1 =, s m =, …, p n0 =0, p n1 =, …, p n, m-1 =,

, p n, m+1 =0, …,

заключаем, что . Наконец, в силу (*) имеем:

.

Если общий член ряда, не являющегося ни сходящимся, ни расходящимся в собственном смысле, стремится к нулю, то частичные суммы этого ряда расположены всюду плотно между их нижним и верхним пределами lim inf и lim sup.

Разобьем числовую прямую на l интервалов точками

.

Существуют в сколь угодно большом удалении конечные последовательности , произвольно медленно нисходящие от верхнего предела последовательности к ее нижнему пределу.

, …

заполняет замкнутый интервал (длина которого равна нулю, если эта последовательность стремится к пределу).

Числовая последовательность, стремящаяся к , имеет наименьший член.

Какое бы число мы ни задали, слева от него будет находиться лишь конечное число членов последовательности, а среди конечного множества чисел существует одно или несколько наименьших.

Сходящаяся последовательность имеет либо наибольший член, либо наименьший, либо и тот и другой.

При совпадении верхней и нижней граней рассматриваемой последовательности теорема тривиальна. Пусть поэтому они различны. Тогда по крайней мере одна из них отличается от предела последовательности. Она и будет равна наибольшему, соответственно наименьшему, члену последовательности.

Пусть числовые последовательности

обладают тем свойством, что

, .

Тогда существует бесконечно много номеров n, для которых одновременно выполняются неравенства

l n s n >l n-1 s n-1, l n s n >l n-2 s n-2, … l n s n >l 1 s 1,

Будем называть l m “выступающим” членом последовательности, если l m больше всех последующих членов. Согласно предположению в первой последовательности содержится бесконечно много выступающих членов; пусть это будут:

,…

,

(*)

отсюда заключаем, что

Если числовая последовательность ,… стремится к и А превышает ее наименьший член, то существует такой номер n (возможно несколько таких), n³ 1, что n отношений

все не больше А, а бесконечное множество отношений

,…

Имеем . Пусть минимум последовательности

u=1, 2, …, n; v=1, 2, 3, …; n=0 исключено в силу предложений относительно А.

.

.

,

Пусть, далее, l 1 >A>0. Тогда существует такой номер n, n ³ 1, что одновременно выполняются все неравенства

.

Если А® 0, то также n® 0.

Тогда . Последовательность

все положительны: коль скоро А меньше наименьшего из них, соответствующий А номер n больше или равен s. Точки (n, L n ) должны быть обтянуты теперь бесконечным выпуклым сверху полигоном.

Источник