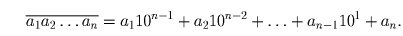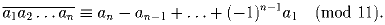Докажите что разность квадратов чисел 105 и 38 делится на 67

Самостоятельная работа «Делимость чисел»

Докажите, что разность квадратов чисел 105 и 38 делится на 67.

Вычеркните в числе 82584703 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите какое-нибудь одно такое число.

Докажите, что число 4·16 12 – 2 40 делится на 33.

Докажите, что сумма пяти последовательных натуральных чисел делится нацело на 5

Найдите трёхзначное число, сумма цифр ко­то­ро­го равна 25, если известно, что его квад­рат де­лит­ся на 16.

Докажите, что сумма кубов чисел 12 и 77 делится на 89.

Вычеркните в числе 181615121 три цифры так, чтобы по­лу­чив­ше­е­ся число де­ли­лось на 12. В от­ве­те ука­жи­те какое-нибудь одно такое число.

Докажите, что число 16 20 +2 76 делится на 17

Докажите что сумма трех последовательных четных чисел кратна 6

Найдите ше­сти­знач­ное на­ту­раль­ное число, ко­то­рое за­пи­сы­ва­ет­ся толь­ко циф­ра­ми 1 и 0 и де­лит­ся на 24.

Докажите, что разность кубов чисел 89 и 25 делится на 64.

Вычеркните в числе 32365427 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.

Докажите, что число 6 18 + 36 8 делится на 37

Докажите что, сумма трёх последовательных нечётных чисел кратна 3.

Найдите четырёхзначное число, крат­ное 75, все цифры ко­то­ро­го раз­лич­ны и нечётны. В от­ве­те ука­жи­те какое-нибудь одно такое число.

Докажите, что разность квадратов чисел 102 и 83 делится на 19.

Вычеркните в числе 141565041 три цифры так, чтобы по­лу­чив­ше­е­ся число де­ли­лось на 30. В от­ве­те ука­жи­те ровно одно по­лу­чив­ше­е­ся число.

Докажите, что число 3 24 – 9 11 + 27 7 делится на 25

Докажите что, сумма четырех последовательных нечётных чисел делится на 8.

Найдите пя­ти­знач­ное число, крат­ное 25, со­сед­ние цифры ко­то­ро­го от­ли­ча­ют­ся на 2. В от­ве­те ука­жи­те какое-нибудь одно такое число.

Докажите, что разность квадратов чисел 102 и 21 делится на 123.

Вычеркните в числе 74513527 три цифры так, чтобы по­лу­чив­ше­е­ся число де­ли­лось на 15. В от­ве­те ука­жи­те ровно одно по­лу­чив­ше­е­ся число.

Докажите, что число 3 19 – 27 6 +9 8 делится на 57

Докажите, что разность квадратов двух последовательных нечетных чисел делится на 8.

Приведите при­мер четырёхзначного числа, крат­но­го 15, про­из­ве­де­ние цифр ко­то­ро­го боль­ше 35, но мень­ше 45. В от­ве­те ука­жи­те ровно одно такое число

Докажите, что сумма кубов чисел 14 и 62 делится на 76.

Вычеркните в числе 123456 три цифры так, чтобы по­лу­чив­ше­е­ся трёхзначное число де­ли­лось на 27. В от­ве­те ука­жи­те по­лу­чив­ше­е­ся число.

Докажите, что число 2 23 – 4 11 + 8 7 делится на 48

Докажите что, сумма четырёх последовательных натуральных чисел не кратна 4.

Приведите при­мер шестизначного на­ту­раль­но­го числа, ко­то­рое записывается толь­ко цифрами 1 и 2 и де­лит­ся на 72. В от­ве­те укажите ровно одно такое число.

Докажите, что разность квадратов чисел 115 и 86 делится на 29.

Вычеркните в числе 75416303 три цифры так, чтобы получившееся число делилось на 30. В ответе укажите какое-нибудь одно получившееся число.

Докажите, что число 4 7 –8 3 делится на 31

Докажите, что сумма трех последовательных натуральных чисел делится на 6.

Найдите четырёхзначное число, крат­ное 18, про­из­ве­де­ние цифр ко­то­ро­го равно 24. В от­ве­те ука­жи­те какое-нибудь одно такое число.

Докажите, что разность кубов чисел 79 и 45 делится на 34.

Вычеркните в числе 23462141 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.

Докажите, что число 9 9 + 27 5 делится на 84

Докажите, что сумма кубов трех последовательных натуральных чисел делится на 9

Приведите при­мер ше­сти­знач­но­го на­ту­раль­но­го числа, ко­то­рое за­пи­сы­ва­ет­ся толь­ко циф­ра­ми 2 и 0 и де­лит­ся на 24. В от­ве­те ука­жи­те ровно одно такое число.

Докажите, что разность квадратов чисел 78 и 21 делится на 99.

Вычеркните в числе 53164018 три цифры так, чтобы по­лу­чив­ше­е­ся число де­ли­лось на 15. В от­ве­те ука­жи­те ровно одно по­лу­чив­ше­е­ся число.

Докажите, что число 2 56 + 16 15 делится на 17

Докажите, что сумма шести последовательных натуральных нечётных чисел делится на 12.

Найдите наи­мень­шее четырёхзначное число, крат­ное 11, у ко­то­ро­го про­из­ве­де­ние его цифр равно 12.

Докажите, что сумма кубов чисел 13 и 36 делится на 49.

Вычеркните в числе 14563743 три цифры так, чтобы получившееся число делилось на 22. В ответе укажите какое-нибудь одно получившееся число.

Докажите, что число 10 10 + 10 делится на 11

Докажите, что сумма пяти последовательных нечётных чисел делится на 5.

Найдите пятизначное натуральное число, кратное 3, сумма цифр которого равна их произведению. В ответе укажите какое-нибудь одно такое число.

Докажите, что разность квадратов чисел 105 и 36 делится на 69.

Вычеркните в числе 123456 три цифры так, чтобы по­лу­чив­ше­е­ся трёхзначное число де­ли­лось на 27.

Докажите, что число 444 88 +888 44 делится на 148

Докажите, что сумма шести последовательных натуральных нечётных чисел делится на 4.

Найдите четырёхзначное на­ту­раль­ное число, крат­ное 11, сумма цифр ко­то­ро­го на 1 мень­ше их произведения.

Докажите, что разность кубов чисел 93 и 45 делится на 48.

Докажите, что число 6 8 + 216 2 делится на 37

Найдите четырёхзначное число, крат­ное 88, все цифры ко­то­ро­го раз­лич­ны и чётны.

Докажите, что разность квадратов чисел 105 и 41 делится на 64.

Вычеркните в числе 89767581 три цифры так, чтобы получившееся число делилось на 18.

Докажите, что число 9 15 –3 27 делится на 26

Найдите че­ты­рех­знач­ное число, крат­ное 66, все цифры ко­то­ро­го раз­лич­ны и четны. В от­ве­те ука­жи­те какое-нибудь такое число

Источник

Докажите что разность квадратов чисел 105 и 38 делится на 67

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .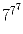

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник

Докажите что разность квадратов чисел 105 и 38 делится на 67

Задача 24:

Докажите, что любое натуральное число сравнимо со своей последней цифрой по модулю а) 10; б) 2; в) 5.

Решение:

Вычтем из числа его последнюю цифру и получим число, оканчивающееся нулем, т.е. делящееся на 10 (а значит, и на 5, и на 2).

Задача 25:

Докажите, что .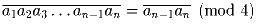

Решение:

Указание: все степени десяти, начиная со 100, делятся на 4.

Задача 26:

Решение:

Число делится на 2 n (на 5 n ) тогда и только тогда, когда число, образованное его последними n цифрами, делится на 2 n (на 5 n ).

Задача 27:

Последняя цифра квадрата натурального числа равна 6. Докажите, что его предпоследняя цифра нечетна.

Решение:

Так как последняя цифра 6, то возводимое в квадрат число четно. Раз оно является квадратом, то оно делится и на 4. Следовательно, число, составленное из двух его последних цифр, должно делиться на 4. Все требуемые двузначные числа легко выписать: 16, 36, 56, 76, 96.

Задача 28:

Предпоследняя цифра квадрата натурального числа – нечетная. Докажите, что его последняя цифра 6.

Решение:

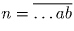
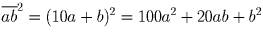
Две последние цифры квадрата числа n зависят только от двух последних цифр числа n. Пусть . Тогда . Ясно, что цифра десятков числа b² должна быть нечетной. Прямой перебор показывает, что цифра единиц должна тогда быть равной 6.

Задача 29:

Докажите, что степень двойки не может оканчиваться четырьмя одинаковыми цифрами.

Решение:

Рассмотрите остатки по модулю 16.

Задача 30:

Найдите 100-значное число без нулевых цифр, которое делится на сумму своих цифр.

Решение:

Подберем число так, чтобы сумма его цифр равнялась 125. Делимость числа на 125 определяется тремя его последними цифрами. Следовательно, годится число 111 … 11599125 (в начале записи единица написана 94 раза).

Задача 31:

Докажите, что любое натуральное число сравнимо с суммой своих цифр по модулю а) 3; б) 9.

Решение:

Ясно, что 10 ≡ 1 (mod %)%9. Поэтому 10 k ≡ 1 (mod 9) для любого натурального k. Таким образом, a ₁ 10 n – 1 + a ₂ 10 n – 2 + … + a _{n – 1} 10¹ + a _n ≡ a ₁ + a ₂ + … + a _n (mod %)%9. Рассуждения для числа 3 совершенно аналогичны.

Задача 32:

Решение:

а) нет; б) нет. Рассмотрите остатки по модулю 9.

Задача 33:

У числа 2¹ºº нашли сумму цифр, у результата снова нашли сумму цифр и т.д. В конце концов получилось однозначное число. Найдите его.

Решение:

Задача 34:

Докажите, что если записать в обратном порядке цифры любого натурального числа, то разность исходного и нового числа будет делиться на 9.

Решение:

Эти числа имеют одинаковые суммы цифр и, значит, одинаковые остатки по модулю 9.

Задача 35:

К числу 15 припишите слева и справа по одной цифре так, чтобы полученное число делилось на 15.

Решение:

Это можно сделать шестью способами: 1155, 4155, 7155, 3150, 6150, 9150.

Задача 36:

Сколько имеется четырехзначных чисел, которые делятся на 45, а две средние цифры у них – 97?

Решение:

Два числа: 6975, 2970.

Задача 37:

Найдите наименьшее натуральное число, делящееся на 36, в записи которого встречаются все 10 цифр.

Решение:

Это число 1023457896.

Задача 38:

Докажите, что произведение последней цифры числа 2 n и суммы всех цифр этого числа, кроме последней, делится на 3.

Решение:

Разберите два случая: последняя цифра равна или не равна 6.

Задача 39:

Может ли сумма цифр точного квадрата равняться 1970?

Решение:

Нет. Рассмотрите остатки по модулю 3.

Задача 40:

Из трехзначного числа вычли сумму его цифр. С полученным числом проделали то же самое и так далее, 100 раз. Докажите, что в результате получится нуль.

Решение:

Задача 41:

Решение:

Задача 42:

Решение:

Указание: 10 ≡ – 1 (mod 11).

Задача 43:

Докажите, что число 111 … 11 (2n единиц) – составное.

Решение:

Это число делится на 11.

Задача 44:

Докажите, что число 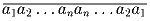– составное.

Решение:

Это число делится на 11.

Задача 45:

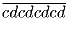
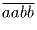
Пусть a, b, c, d – различные цифры. Докажите, что не делится на .

Решение:

делится на 11, а – нет.

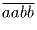
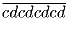
Задача 46:

A – шестизначное число, в записи которого по одному разу встречаются цифры 1, 2, 3, 4, 5, 6. Докажите, что A не делится на 11.

Решение:

Цифры 1, 2, 3, 4, 5, 6 нельзя разбить на две тройки, разность сумм в которых делится на 11.

Задача 47:

Докажите, что разность числа, имеющего нечетное количество цифр, и числа, записанного теми же цифрами, но в обратном порядке, делится на 99.

Решение:

Эти два числа имеют одинаковые остатки как при делении на 9, так и при делении на 11.

Задача 48:

Можно ли составить из цифр 2, 3, 4, 9 (каждую цифру можно использовать сколько угодно раз) два числа, одно из которых в 19 раз больше другого?

Решение:

Нельзя. Проследите за последней цифрой.

Задача 49:

Сумма двух цифр a и b делится на 7. Докажите, что число 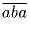также делится на 7.

Решение:

.

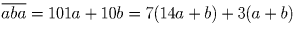
Задача 50:

Сумма цифр трехзначного числа равна 7. Докажите, что это число делится на 7 тогда и только тогда, когда две его последние цифры равны.

Решение:

, так как 2(a + b + c) ≡ 0 (mod 7). Значит, делится на 7 тогда и только тогда, когда b – c делится на 7. Но так как b, c

Источник

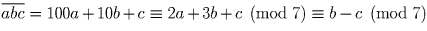
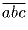
Докажите что разность квадратов чисел 105 и 38 делится на 67

Логический прием, использованный в приведенном доказательстве, называется принципом Дирихле – по имени Петера Густава Дирихле (1805-1895) немецкого математика, автора описанного метода.

Вот общая форма принципа Дирихле:

Если k∙n+1 предмет разложен в k ящиков, то, по крайней мере, в одном из ящиков лежит не меньше, чем n+1 предмет.

По традиции в популярной литературе принцип Дирихле объясняют на примере “зайцев” и “клеток’:

Если N зайцев сидят в n клетках и N>n, то хотя бы в одной клетке сидит более одного зайца.

Этим принципом в неявном виде пользовался, например, Ферма в XVII веке; но широко применяться в доказательствах он стал лишь с прошлого века! Несмотря на свою простоту, это рассуждение оказалось чрезвычайно плодотворным. Вот только один пример. Если делить одно целое число на другое, например 1 на 7, что мы получим? Будем делить в столбик, получая все новые и новые остатки. Но поскольку остатками от деления на 7 могут быть лишь числа 1, 2, 3, 4, 5, 6 и 0, мы либо должны на каком-то шаге получить 0 и остановиться, либо после шестого деления один из остатков обязан повториться. Дальше делить нет смысла — этот остаток мы уже разделили на 7, и все результаты у нас перед глазами. Ясно, что деление будет продолжаться бесконечно, но мы будем получать снова и снова одну и ту же последовательность цифр — период.

Выходит, при делении целого числа на целое мы получим либо конечную десятичную дробь, либо периодическую — и более ничего!

Как видим – все гениальное просто, и к этому же относится и принцип Дирихле.

В лесу растет миллион елок. Известно, что на каждой из них не более 600000 иголок. Докажите, что в лесу найдутся две елки с одинаковым числом иголок.

Перед нами миллион «кроликов»-елок и, увы, всего лишь 600001 клетка с номерами от 0 до 600000. Каждый «кролик»-елка сажается нами в клетку с номером, равным количеству иголок на этой елке. Так как «кроликов» гораздо больше, чем клеток, то в какой-то клетке сидит по крайней мере два «кролика» – если бы в каждой сидело не более одного, то всего «кроликов»-елок было бы не более 600001 штук. Но ведь, если два «кролика»-елки сидят в одной клетке, то количество иголок у них одинаково.

Дано 12 целых чисел. Докажите, что из них можно выбрать два, разность которых делится на 11.

Остатки по модулю 11 – «клетки», числа – «кролики».

В городе Ленинграде живет более 5 миллионов человек. Докажите, что у каких-то двух из них одинаковое число волос на голове, если известно, что у любого человека на голове менее миллиона волос.

Постройте миллион клеток с номерами от 0 до 999999 и рассадите там людей, поместив каждого ленинградца в клетку, номер которой равен количеству волос на его голове.

В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта.

25 ящиков-«кроликов» рассадим по 3 клеткам-сортам. Так как 25 = 3 • 8 + 1, то применим «обобщенный принцип Дирихле» для N = 3, k = 8 и получим, что в какой-то клетке-сорте не менее 9 ящиков.

В стране Курляндии m футбольных команд (по 11 футболистов в каждой). Все футболисты собрались в аэропорту для поездки в другую страну на ответственный матч. Самолет сделал 10 рейсов, перевозя каждый раз по m пассажиров. Еще один футболист прилетел к месту предстоящего матча на вертолете. Докажите, что хотя бы одна команда была целиком доставлена в другую страну.

Так как перевезено всего 10m + 1 футболистов, то, рассадив их по клеткам-командам, получаем, что в какой-то клетке сидит 11 футболистов.

Дано 8 различных натуральных чисел, не больших 15. Докажите, что среди их положительных попарных разностей есть три одинаковых.

Различных разностей может быть 14 – от 1 до 14 – это те 14 клеток, в которые мы будем сажать кроликов. Кто же будет нашими кроликами? Ими, конечно, должны быть разности между парами данных нам натуральных чисел. Однако имеется 28 пар и их можно рассадить по 14 клеткам так, что в каждой клетке будет сидеть ровно два «кролика» (и значит, в каждой меньше трех). Здесь надо использовать дополнительное соображение: в клетке с номером 14 может сидеть не более одного кролика, ведь число 14 можно записать как разность двух натуральных чисел, не превосходящих 15, лишь одним способом: 14 = 15 – 1. Значит, в оставшихся 13 клетках сидят не менее 27 кроликов, и применение обобщенного принципа Дирихле дает нам желаемый результат.

Докажите, что в любой компании из 5 человек есть двое, имеющие одинаковое число знакомых в этой компании.

Вариантов числа знакомых всего 5: от 0 до 4. Осталось заметить, что если у кого-то 4 знакомых, то ни у кого не может быть 0 знакомых.

Несколько футбольных команд проводят турнир в один круг. Докажите, что в любой момент турнира найдутся две команды, сыгравшие к этому моменту одинаковое число матчей.

Пусть всего команд n. Тогда вариантов числа команд, с которыми сыграла данная команда n: от 0 до n – 1. Осталось заметить, что если одна команда сыграла со всеми n – 1-й, то никакая другая команда не могла ни с кем не сыграть.

10 школьников на олимпиаде решили 35 задач, причем известно, что среди них есть школьники, решившие ровно одну задачу, школьники, решившие ровно две задачи и школьники, решившие ровно три задачи. Докажите, что есть школьник, решивший не менее пяти задач.

Из условий следует, что найдутся 7 школьников, решивших 35 – 6 = 29 задач. Так как 29 = 4 • 7 + 1, то найдется школьник, решивший не менее пяти задач.

Какое наибольшее число королей можно поставить на шахматной доске так, чтобы никакие два из них не били друг друга?

Ответ: 16 королей. Разобьём доску на 16 квадратиков, в каждом может быть не более одного короля.

Докажите, что равносторонний треугольник нельзя покрыть двумя меньшими равносторонними треугольниками.

Каждый из меньших треугольников не может накрывать более одной вершины большого треугольника.

В квадрат со стороной 1 метр бросили 51 точку. Докажите, что какие-то три из них можно накрыть квадратом со стороной 20 см.

Разобьем наш квадрат на 25 квадратов со стороной 20 см. По обобщенному принципу Дирихле, в какой-то из них попадет по крайней мере три точки из 51 брошенной.

Пятеро молодых рабочих получили на всех зарплату – 1500 рублей. Каждый из них хочет купить себе магнитофон ценой 320 рублей. Докажите, что кому-то из них придется подождать с покупкой до следующей зарплаты.

Если бы каждый из рабочих мог купить магнитофон, то у них в сумме было бы не менее 5 • 320 = 1600 рублей.

В бригаде 7 человек и их суммарный возраст – 332 года. Докажите, что из них можно выбрать трех человек, сумма возрастов которых не меньше 142 лет.

Покрасим всю сушу в синий цвет, а все точки, диаметрально противоположные суше – в красный. Тогда обязательно есть точка, которая покрашена в оба цвета. В ней и надо рыть туннель.

Докажите, что среди степеней двойки есть две, разность которых делится на 1987.

Рассмотрите 1988 степеней и их остатки по модулю 1987.

Докажите, что из 52 целых чисел всегда найдутся два, разность квадратов которых делится на 100.

Квадраты при делении на 100 могут давать лишь 51 остаток, так как остатки x и 100 – x при возведении в квадрат дают один и тот же остаток.

Докажите, что среди чисел, записываемых только единицами, есть число, которое делится на 1987.

Рассмотрим 1988 чисел-«кроликов» 1, 11, 111, …, 111 … 11 (1988 единиц) и посадим их в 1987 клеток с номерами 0, 1, 2, …, 1986 – каждое число попадает в клетку с номером, равным остатку от деления этого числа на 1987. Тогда (по принципу Дирихле) найдутся два числа, которые имеют одинаковые остатки при делении на 1987. Пусть это числа 11 … 11 (m единиц) и 11 … 11 (n единиц), причем m > n. Но их разность, которая делится на 1987, равна 11 … 1100 … 00 (m – n единиц и n нулей). Сократим все нули – ведь они не имеют никакого отношения к делимости на 1987 – и получим число из одних единиц, которое делится на 1987.

Докажите, что существует степень тройки, оканчивающаяся на 001.

Если 3m и 3n – степени тройки, дающие один и тот же остаток при делении на 1000, то 3m – 3n = 3n(3m – n – 1) делится на 1000 (мы считаем для определенности, что m > n).

Эти суммы могут принимать лишь 7 разных значений: от – 3 до 3.

Сто человек сидят за круглым столом, причем более половины из них – мужчины. Докажите, что какие-то два мужчины сидят друг напротив друга.

Разобьем всех людей на 50 пар так, что в каждой паре – два человека, сидящих друг напротив друга. Ясно, что в одной из этих пар-«клеток» оба человека – мужчины.

15 мальчиков собрали 100 орехов. Докажите, что какие-то два из них собрали одинаковое число орехов.

Если это не так, то, очевидно, что мальчики собрали не менее, чем 0 + 1 + 2 + … + 14 = 105 орехов – противоречие.

Цифры 1, 2, …, 9 разбили на три группы. Докажите, что произведение чисел в одной из групп не меньше 72.

Произведение чисел во всех группах равно 9! = 362880, а 71? = 357911.

Поскольку от любой клетки до любой другой можно добраться, не более 19 раз сдвинувшись в соседнюю клетку, то все числа находятся между числами a и a + 95, где a – минимальное из всех расставленных чисел. Значит, среди этих чисел не более 96 различных.

Докажите, что среди любых 6 человек есть либо трое попарно знакомых, либо трое попарно незнакомых.

У данного человека среди остальных пяти есть либо не менее трех знакомых, либо не менее трех незнакомых ему. Разберем, например, первый случай. Среди этих трех людей есть либо двое знакомых – тогда они вместе с выбранным нами исходно человеком образуют нужную тройку, либо они все трое попарно незнакомы.

На клетчатой плоскости дано 5 произвольных узлов сетки. Докажите, что середина одного из отрезков, соединяющих какие-то две из этих точек, также является узлом сетки.

Рассмотрите координаты этих точек и их остатки при делении на 2.

На складе имеется по 200 сапог 41, 42 и 43 размеров, причем среди этих 600 сапог 300 левых и 300 правых. Докажите, что из них можно составить не менее 100 годных пар обуви.

В каждом размере каких-то сапог меньше: правых или левых. Выпишем эти типы сапог по размерам. Какой-то тип, например, левый, повторится по крайней мере дважды, например, в 41 и 42 размерах. Но так как количество левых сапог в этих размерах суммарно не меньше 100 (почему?), то мы имеем не менее 100 годных пар обуви в этих размерах.

В алфавите языка племени Ни-Бум-Бум 22 согласных и 11 гласных, причем словом в этом языке называется произвольное буквосочетание, в котором нет двух согласных подряд и ни одна буква не использована дважды. Алфавит разбили на 6 непустых групп. Докажите, что из всех букв одной из групп можно составить слово.

Докажите, что в одной из групп разность между числом согласных и числом гласных не больше 1.

Докажите, что среди любых 10 целых чисел найдется несколько, сумма которых делится на 10.

Рассмотрите 10 сумм: x₁, x₁ + x₂, …, x₁ + x₂ + … + x₁₀ и их остатки при делении на 10.

Дано 11 различных натуральных чисел, не больших 20. Докажите, что из них можно выбрать два числа, одно из которых делится на другое.

Разбейте числа от 1 до 20 на 10 наборов, в каждом из которых в любой паре чисел одно делится на другое: 11, 13, 15, 17, 19, 1,2,4,8,16, 3,6,12, 5,10,20, 7,14, 9,18.

Источник