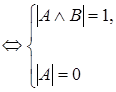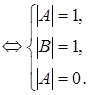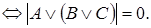Докажите что следующая формула является тавтологией
1. Высказывания, формулы, тавтологии
Определение. Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).
То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.
Пример. “Москва – столица России” – истинное высказывание.
“5 –четное число” – ложное высказывание.
“

“Студент второго курса” не высказывание (не является утверждением).
Высказывания бывают элементарные и составные.
Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.
Пример. “Число 22 четное” – элементарное высказывание.
“Число 22 четное и делится на 11” – составное высказывание.
Высказывания обозначают заглавными буквами латинского алфавита: 

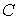
При фиксированном множестве букв 




Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.
К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются Формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.
Таблицы истинности основных логических операций.
Более строго формула определяется так.
Определение. 1) Всякая буква есть формула.
2) Если 




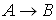
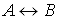
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).
В классической логике формулы принято заключать в круглые скобки, но в мы этого делать не будем. Для всякой формулы можно построить таблицу истинности.
Значение формулы 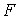




Часть формулы, которая сама является формулой, называется Подформулой данной формулы.
Определение. Формула называется Тавтологией, если она принимает только истинные значения при любых значениях букв.
Другими словами, тавтология – это тождественно истинная формула.
Установить, является ли формула тавтологией, можно:
– по таблице истинности,
– используя свойства логических операций.
Из курса дискретной математики известны основные логические эквивалентности (свойства логических операций), которые являются примерами тавтологий.
1. Коммутативность: 





4. Идемпотентность: 

5. Закон двойного отрицания: 
6. Закон исключения третьего: 
7. Закон противоречия: 
8. Законы де Моргана:


9. Свойства операций с логическими константами:




Здесь 

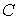
Примеры. 1. Доказать, что формула 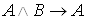
Доказательство. Допустим, что при некоторых значениях букв (то есть в некоторой интерпретации)
Приходим к противоречию, которое доказывает, что исходная формула – тавтология.
2. Доказать, что формула 
Доказательство. Эквиваленция истинна, если левая и правая части принимают одинаковые значения на некотором наборе значений букв.
Допустим, что при некоторых значениях букв
Следовательно, исходная формула – тавтология.
3. Доказать, что формула 
Доказательство. Допустим, что при некоторых значениях букв
Следовательно, исходная формула – тавтология.
Таким образом, тождественную истинность импликации удобно доказывать от противного, а тождественную истинность эквиваленции установлением равенства значений левой и правой части.
Теорема. Пусть формулы 
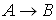

Доказательство. Пусть 



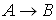






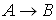







Теорема. Пусть формула 








Доказательство аналогично доказательству предыдущей теоремы.
Докажите,что следующие формулы являются тавтологиями

Всем привет! Подскажите пожалуйста как быть с данным заданием: Спасибо
Докажите, что в описанном ниже исчислении высказываний для любых формул F, G и H выводимы следующие формулы
Мне нужна помощь, как выполнить доказательство? Подскажите кто чем может (по теме). Докажите.
Записать формулы, выражающие следующие утверждения
Пусть предметная область D — это множество людей, на котором определены такие предикаты: E(x, y) —.
Добавлено через 6 минут

Определить, являются ли следующие функции самодвойственными(Вложения) Подскажите правильные ли.
Выяснить, являются ли верными следующие выводы формул
Заранее всем спасибо за Ваши ответы! Буду очень благодарен 🙂

Приведите к предваренной нормальной форме следующие формулы логики предикатов.
Приведите к предваренной нормальной форме следующие формулы логики предикатов
Добрый день\вечер, не могли ли вы мне пожалуйста помочь с данной задачей потому что я тупой и не.
04. Тавтология и противоречие
Определение. Тавтологией Называется составное высказывание, истинное при Всех Наборах истинностных значений составляющих его простых высказываний.
Определение. Противоречием называется составное высказывание, ложное при Всех Наборах истинностных значений составляющих его простых высказываний.
Пример. Доказать, что высказывание 

Решение. Для доказательства составим общую таблицу истинности для этих формул.
При всех истинностных значениях высказывания А высказывание 

Теорема 1.3. Отрицанием тавтологии является противоречие, отрицанием противоречия является тавтология.
Доказательство. 1) Рассмотрим формулу, являющуюся тавтологией. По определению, при всех наборах истинностных значений составляющих её простых высказываний она принимает значение «истина». Тогда, по определению, отрицание данной формулы при всех наборах истинностных значений составляющих её простых высказываний принимает значение «ложь». Значит, отрицание тавтологии является противоречием.
2) Рассмотрим формулу, являющуюся противоречием. По определению, при всех наборах истинностных значений составляющих её простых высказываний она принимает значение «ложь». Тогда, по определению, отрицание данной формулы при всех наборах истинностных значений составляющих её простых высказываний принимает значение «истина». Значит, отрицание противоречия является тавтологией. ■
Задачи и упражнения
1.14. Докажите, что следующие составные высказывания являются тавтологиями:
1) 
2) 
3) 
4) 
5) 
1.15. Докажите, что следующие составные высказывания являются противоречиями:
1) 


Доказать двумя способами,что следующая формула является тождественно истинной (тавтологией)
Выяснить двумя способами, является ли данная формула тавтологией
1. Выяснить 2-мя способами(при помощи равносильных преобразований и таблиц истинности) являются ли.

Добрый день! Подскажите, как решать такие задания: (A\supset C)\supset ((B\supset C)\supset ((A.
Установить, является ли данная формула тождественно-истинной
Установить, является ли данная формула тождественно-истинной. Пример Подскажите с чего начать?
Доказать, что формула не является логически истинной
помогите.у меня получается тождественно истинна вот так у меня вот крупнее
Добавлено через 6 минут
или так:

Нужно доказать, что данная формула является тавтологией: (А => (B => C)) => ((A =>B) => (A =>C)).

Доказать, что формула является тавтологией F=¬(А->¬( B&A))->AVB с помощью эквивалентных.
Глава 1. Высказывания, формулы, тавтологии
Определение.Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).
То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.
Пример.“Москва – столица России” – истинное высказывание.
“5 –четное число” – ложное высказывание.
“ 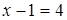
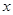
“Студент второго курса” не высказывание (не является утверждением).
Высказывания бывают элементарные и составные.
Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.
Пример.“Число 22 четное” – элементарное высказывание.
“Число 22 четное и делится на 11” – составное высказывание.
Высказывания обозначают заглавными буквами латинского алфавита: 
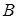
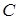
При фиксированном множестве букв 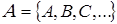
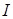
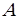
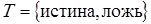

Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.
К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.
Таблицы истинности основных логических операций.
 | 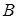 | 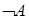 |  |  |  |  |
Более строго формула определяется так.
Определение.1) Всякая буква есть формула.
2) Если 
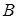
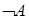
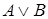
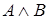
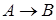
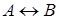
3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).
В классической логике формулы принято заключать в круглые скобки, но в мы этого делать не будем. Для всякой формулы можно построить таблицу истинности.
Значение формулы 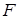
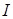
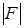


Часть формулы, которая сама является формулой, называется подформулой данной формулы.
Определение. Формула называется тавтологией, если она принимает только истинные значения при любых значениях букв.
Другими словами, тавтология – это тождественно истинная формула.
Установить, является ли формула тавтологией, можно:
– по таблице истинности,
– используя свойства логических операций.
Из курса дискретной математики известны основные логические эквивалентности (свойства логических операций), которые являются примерами тавтологий.
1. Коммутативность: 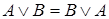
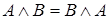
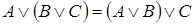

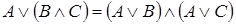

4. Идемпотентность: 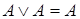
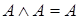
5. Закон двойного отрицания: 
6. Закон исключения третьего: 
7. Закон противоречия: 
8. Законы де Моргана:
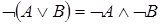

9. Свойства операций с логическими константами:
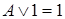
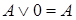

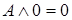
Здесь 
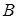
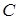
Примеры.1. Доказать, что формула 
Доказательство. Допустим, что при некоторых значениях букв (то есть в некоторой интерпретации)

Приходим к противоречию, которое доказывает, что исходная формула – тавтология.
2. Доказать, что формула 
Доказательство. Эквиваленция истинна, если левая и правая части принимают одинаковые значения на некотором наборе значений букв.
Допустим, что при некоторых значениях букв
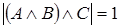
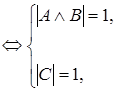
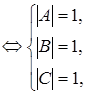
Следовательно, исходная формула – тавтология.
3. Доказать, что формула 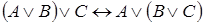
Доказательство. Допустим, что при некоторых значениях букв
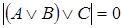
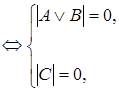

Следовательно, исходная формула – тавтология.
Таким образом, тождественную истинность импликации удобно доказывать от противного, а тождественную истинность эквиваленции установлением равенства значений левой и правой части.
Теорема.Пусть формулы 
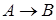
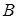
Доказательство. Пусть 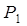
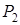
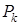

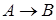

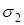


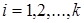

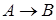
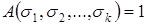
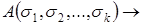
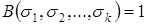
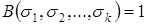

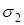

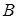
Теорема. Пусть формула 
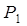
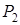



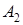
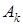

Доказательство аналогично доказательству предыдущей теоремы.