Докажите что сумма квадратов двух нечетных чисел не является квадратом целого числа
Докажите что сумма квадратов двух нечетных чисел не является квадратом целого числа
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Решение
Первый способ. Остаток от деления на 4 квадрата нечётного числа равен 1, а остаток квадрата чётного числа равен 0. Поэтому указанная сумма при делении на 4 даёт остаток 2 или 3, то есть не является квадратом.
Второй способ. (n – 2)² + (n – 1)² + n² + (n + 1)² + (n + 2)² = 5n² + 10 = 5(n² + 2), а n² + 2 не делится на 5.
Источники и прецеденты использования
| книга | |
| Автор | Генкин С.А., Итенберг И.В., Фомин Д.В. |
| Год издания | 1994 |
| Название | Ленинградские математические кружки |
| Издательство | Киров: «АСА» |
| Издание | 1 |
| глава | |
| Номер | 4 |
| Название | Делимость и остатки |
| Тема | Теория чисел. Делимость |
| задача | |
| Номер | 040 |
| книга | |
| Автор | Алфутова Н.Б., Устинов А.В. |
| Год издания | 2002 |
| Название | Алгебра и теория чисел |
| Издательство | МЦНМО |
| Издание | 1 |
| глава | |
| Номер | 4 |
| Название | Арифметика остатков |
| Тема | Деление с остатком. Арифметика остатков |
| параграф | |
| Номер | 3 |
| Название | Сравнения |
| Тема | Деление с остатком. Арифметика остатков |
| задача | |
| Номер | 04.099 |
Теория чисел
В теории чисел есть множество разнообразных задач, как решенных, так и нет, как очень сложных, так и доступных любому, кто имеет начальный уровень в математике. Их решение зачастую не требует каких-то специальных знаний и навыков, необходим лишь здравый смысл и присутствие логики.
В конце статьи приведен список литературы, которая послужила источником приведенных здесь задач.
Задачи на делимость
Задача Найти число делителей и сумму делителей числа 720.
Решение: Каноническое раpложение числа 720 = 2 4 *3 2 *5
Найдем сумму делителей по формуле:
Найдем число делителей числа 720:
N = (4+1)(2+1)(1+1) = 30
Задача Если сумма двух трехзначных чисел делится на 37, то и шестизначное число, составленное приписыванием одного из них к другому, также делится на 37.
Доказательство: Если N1=abc и N2=def, то abcdef=N1*10 3 + N2 = (N1 + N2) + 999N1.
(N1 + N2) делится на 37 по определению, а 999 кратно 37.
Задачи на нахождение наибольшего общего делителя (НОД) и наименьшего общего кратного [НОК]
Задача Найти НОД для следующих чисел:
1. d = (a,b) и m = [a,b]
2. ab и m = [a,b]
3. a+b и m=[a,b]
Решение:
1. (d, m) = (d, [dx, dy]) = d(1, [x, y]) = d
2. (ab, m) = (dm, m)=m(d, 1) = m, где d=(a, b)
3. Пусть (a, b)=d и a = dx, b = dy, где (x, y) = 1. Тогда (a+b, m) = (d(x+y), dxy) = (d(x+y, xy) = d. Следовательно, (а+b, [a, b]) = (a, b).
Задача Решить систему уравнений:
x+y=150
(x,y)=30
Решение:
Второе уравнение равносильно системе из 3 уравнений:
x=30u
y=30v
(u,v)=1
После подстановки в первое уравнение получаем: u+v=5, откуда u может принимать значения 1,2,3,4. Отсюда x=30,60,90,120. y=120,90,60,30.
Задачи о простых числах
Задача Разложить на простые множители число 30!
Решение:
Разложение имеет вид:
30! = 2 a1 + 3 a2 + 5 a3 + 7 a4 + 11 a5 + 13 a6 + 17 a7 + 19 a8 + 23 a9 + 29 a10
Найдем a1 = |30/2| + |30/4| + |30/8| + |30/16| = 26
Найдем a2 = |30/3| + |30/9| + |30/27| = 14
Найдем a3 = |30/5| + |30/25| = 7
И т.д. В результате
30! = 2 26 + 3 14 + 5 7 + 7 4 + 11 2 + 13 2 + 17 + 19 + 23 + 29
Задача Доказать, что по модулю 4 множество всех простых чисел может быть разбито на два подмножества: на простые числа вида 4п+1 и на простые числа вида 4n+3
Доказательство: Множество всех натуральных чисел по модулю 4 может быть разбито на 4 подмножества (по числу возможных остатков): на числа вида 4п, 4n+1, 4n+2 и 4n+З. Числа вида 4п и вида 4n+2 составные. Следовательно, все простые числа содержатся среди натуральных чисел вида 4n+l и вида 4n+З.
Разные задачи
Задача Дано целое число A, у которого есть взаимно-простые с ним числа n. Также у этого числа A имеются простые делители p. Убедиться в справедливости следующего равенства:
S = ∑ μ(d)*Sd
Введение (стр. 2 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Поскольку сумма никаких двух из чисел 1,4,5,6,7,9, 11, 16 и 17 не кратна 19, приходим к выводу: сумма квадратов двух целых чисел кратна 19 в том и только том случае, когда слагаемые кратны 19.
Свойство простых чисел, не являющихся суммами двух квадратов
Как относиться к трудностям? В области неведомого надо рассматривать трудности как скрытый клад! Обычно: чем труднее, тем полезнее. Не так ценно, если трудности возникают от твоей борьбы с самим собой. Но когда трудности исходят от увеличившегося сопротивления предмета — это прекрасно!!
Чем больше по величине простое число р, тем больше квадратичных вычетов по модулю р. Поэтому пора менять метод исследования: если мы не желаем погрязнуть в нескончаемых вычислениях, то должны каким-то одним общим рассуждением охватить числа 3, 7, 11, 19 и многие другие простые числа.
Пока не вполне ясно, что это за числа и чем они отличаются от чисел 2, 5, 13, 17. Впрочем, одно отличие очевидно: числа 3,7,11,19 не представимы, а числа 2, 5, 13,17 представимы в виде суммы квадратов двух целых чисел. Кроме того, простые числа р = 3, 7, 11, 19 обладают, как мы уже доказали, тем свойством, что если сумма квадратов целых чисел кратна р, то каждое из слагаемых кратно р. Продолжив (довольно утомительные, если не использовать компьютер) вычисления, можно доказать это свойство для р = 23, 31, 43, 47, 59, 67, 71, 79, 83, 87. Осечки ни разу не будет:
Теорема 2. Если простое число р не представимо в виде суммы двух квадратов и если сумма квадратов х2 + у2 кратна р, то каждое из целых чисел х, у кратно р.
Мы получим эту теорему как одно из следствий теории целых гауссовых чисел. Поскольку это не так уж просто, давайте отвлечемся на некоторое время от теоремы 2 и обратим внимание на другое свойство рассматриваемых простых чисел 3, 7, 11. 83, 87: при делении на 4 они дают остаток 3.
Числа вида 4n + 3
В виде суммы двух квадратов не представимы не только простые числа, которые при делении на 4 дают остаток 3, но и вообще все числа 3,7, 11, 15, 19,23,27.
Теорема 3. Всякое представимое в виде суммы квадратов двух целых чисел нечетное число при делении на 4 дает остаток 1, а не 3.
Доказательство. Из двух квадратов, сумма которых нечетна, обязательно один четен, а другой нечетен. Квадрат четного числа нацело делится на 4, а квадрат нечетного числа при делении на 4 дает остаток 1 (проверьте!).
Произведение сумм квадратов
Мы уже нашли несколько признаков непредставимости числа в виде суммы двух квадратов. Не менее важны признаки представимости. Начнем с того, что если n = x2 + y2, то
Значит, вместе с каждым представимым числом n представимо и число 2n. Далее,
Легко проверить и формулы
Все они являются частными случаями общей формулы, которая представляет произведение сумм двух квадратов в виде суммы двух квадратов. Чтобы получить ее, раскроем скобки
прибавим и отнимем 2аbху и изменим порядок слагаемых:
Упражнение 8. Докажите, что
а) если четное число n есть сумма квадратов двух целых чисел, то и число n/2 представимо в виде суммы квадратов двух целых чисел;
б)* если кратное 5 число n есть сумма квадратов двух целых чисел, то число n/5 тоже представимо в таком виде;
в)* если 13k = х2 + у2, где k, х, у — целые числа, то хотя бы одна из формул 
Теорема Ферма — Эйлера
Поскольку мы научились представлять произведение сумм двух квадратов в виде суммы двух квадратов, очень важно выяснить, какие простые числа представимы в виде суммы двух квадратов целых чисел, а какие не представимы. Числа вида 4n + 3, как утверждает теорема 3, не представимы. Поэтому рассмотрим простые числа, которые при делении на 4 дают остаток 1. Это: 5 = 22 + 12, 13 = 32 + 22, 17 = 42 + 12, 29 = 52 + 22, 37 = 62 + 12, 41 = 52 + 42, 53 = 72 + 22.
Теорема 4. Любое простое число р, которое при делении на 4 дает остаток 1, представимо в виде суммы квадратов двух натуральных чисел.
Мы приведем доказательство, состоящее из следующих двух лемм.
Лемма 1. Для любого простого числа р == 4n + 1, где 
Лемма 2. Любой простой делитель р числа m2 + 1, где m — целое, представим в виде суммы квадратов двух натуральных чисел.
Упражнение 9. Пользуясь формулой (1), объясните, почему в лемме 2 слова «любой простой» можно заменить на «любой натуральный».
Лемму 1 мы выведем из теоремы Вильсона (1741- 1793), лемму 2 — из теории делимости целых гауссовых чисел. Но сначала сформулируем ответ на один важный вопрос.
Какие натуральные числа — суммы двух квадратов?
По теоремам 3 и 4, простое число р > 2 не представимо в виде суммы двух квадратов, если оно имеет вид р = 4k + 3, и представимо — если р = 4k + 1, где k — целое. Вспомнив формулу (1) и применив (еще не доказанную нами) теорему 2, получаем следующий элегантный критерий: натуральное число представимо в виде суммы квадратов двух целых чисел тогда и только тогда, когда в его разложение на простые множители любой простой множитель вида 4k + 3 входит в четной степени.
Этот критерий впервые был сформулирован голландцем Альбером Жираром (1595-1632) в следующем виде: натуральное число представимо в виде суммы двух квадратов тогда и только тогда, когда оно является или квадратом, или числом 2, или простым числом, которое на 1 больше, чем некоторое кратное 4, или произведением нескольких вышеперечисленных чисел. Скорее всего, Жирар опирался лишь на изучение таблиц и не претендовал на то, что может доказать необходимость и достаточность своих условий.
Доказательство леммы 1
В качестве числа m в лемме 1 годится m = (2n)!, т. е. произведение первых 2n натуральных чисел. Чтобы это увидеть, рассмотрим число
Оно дает при делении на р такой же остаток, как и число
Докажите что сумма квадратов двух нечетных чисел не является квадратом целого числа
Задача 15:
Найдите остатки от деления
а) 1989 1990 1991 + 1992³ на 7;
Решение:
Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.
Задача 16:
Докажите, что n³ + 2n делится на 3 для любого натурального n.
Решение:
Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.
Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.
Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.
Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.
Задача 17:
Докажите, что n 5 + 4n делится на 5 при любом натуральном n.
Решение:
Указание: Переберите остатки от деления на 5.
Задача 18:
Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 3.
Задача 19:
Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 9.
Задача 20:
Докажите, что n³ – n делится на 24 при любом нечетном n.
Решение:
Указание: Докажите, что указанное число делится и на 3, и на 8.
Задача 21:
а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.
б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.
Решение:
Указание: Докажите, что указанные числа делятся и на 3 и на 8.
Задача 22:
Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.
Решение:
Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.
Задача 23:
a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.
Решение:
Проверьте, что и a и b делятся и на 3 и на 7.
Задача 24:
a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.
Решение:
Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.
Задача 25:
Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.
Решение:
Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.
Задача 26:
Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.
Решение:
Выясните возможные остатки квадратов при делении на 8.
Задача 27:
Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.
Решение:
Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.
Задача 28:
Решение:
Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 9 = 81), а за 1 – 9 (1 9 = 9).
Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.
Задача 29:
Решение:
Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.
Задача 30:
Решение:
Задача 31:
Найдите остаток от деления 2¹ºº на 3.
Решение:
Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».
Задача 32:
Найдите остаток от деления 3 1989 на 7.
Решение:
Задача 33:
Докажите, что 2222 5555 + 5555²²²² делится на 7.
Решение:
Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.
Задача 34:
Найдите последнюю цифру числа 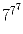
Задача 35:
а) p, p + 10, p + 14 – простые числа. Найдите p.
б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.
Решение:
Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.
Задача 36:
p и 8p² + 1 – простые числа. Найдите p.
Решение:
Задача 37:
p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.
Решение:
Задача 38:
Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.
Решение:
Рассмотрите остатки по модулю 3.
Задача 39:
а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?
б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 40:
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 41:
p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.
Ответ: p = 5. Рассмотрите остатки при делении на 5.
Задача 42:
Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.
Решение:
Это число дает остаток 7 от деления на 9.
Задача 43:
Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.
Решение:
Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.
Задача 44:
Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.
Решение:
Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.
Задача 45:
x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.
Решение:
Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.
Применение свойств квадрата целого числа в решении задач на делимость
Разделы: Математика
Цель: формирование знаний, умений и навыков при решении в целых числах уравнений, содержащих квадрат целого числа; создание условий для преодоления у выпускников трудностей при решении заданий ( 
Задачи:
Тип занятия: урок изучения нового материала.
Ход урока
I. Постановка цели
В 2009-2010 учебном году на ЕГЭ по математике задания 
II. Актуализация опорных знаний
При решении задач нам пригодятся признаки делимости чисел, с которыми вы познакомились ещё в 6-ом и последующих классах, а также определение числа
Напомните, пожалуйста, признаки делимости:
И ещё вопрос: что такое 
n! = 1
2
3
4
5
6
…
n – произведение первых n натуральных чисел.
1! = 1
2! = 12 = 2
3! = 12
3 = 6
4! = 12
3
4 = 24
5! = 12
3
4
5 = 120
6! =12
3
4
5
6 = 720 и т.д.
При n≥5 число n! всегда оканчивается нулём.
III. Ознакомление с новым материалом
Рассмотрим таблицу квадратов натуральных чисел. Все свойства точного квадрата числа спрятаны в этой таблице. Нам только надо проявить наблюдательность при анализе данных в таблице.
| к | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | … |
Обратите внимание на последние цифры квадратов чисел. Что вы заметили?
На какие натуральные числа может делиться точный квадрат числа?
Свойства квадрата целого числа
Точный квадрат целого числа не может оканчиваться цифрами 2, 3, 7, 8, а также нечётным количеством нулей.
Первое свойство очевидное и доказательства не требует.
Квадрат натурального числа либо делится на 4, либо при делении на 8 даёт остаток 1.
Доказательство:
Если а – число чётное, то есть а = 2к, то 


Если а – число нечётное, то есть а = 2к + 1, то 


Квадрат натурального числа либо делится на 9, либо при делении на 3 даёт остаток 1.
Доказательство:
Если число а кратно 3, значит а = 3к, тогда 


Если же число а не кратно 3, то оно имеет вид а = 3к ± 1, тогда 


Вот мы и сформулировали свойства точного квадрата числа. Теперь вашему вниманию я предлагаю ряд задач, в решении которых используются вышеперечисленные свойства.
1. Найти все натуральные n, при которых число 
Решение:
Если n=1, то
– не является точным квадратом.
Если n=2, то– не является точным квадратом.
Если n=3, то– не является точным квадратом.
Если n=4, то, значит, при n=4 число
является точным квадратом числа.
Если, то
оканчивается 0, тогда
оканчивается 7, но по свойству (1) квадрат целого числа не может оканчиваться цифрой 7. Значит, других натуральных чисел n, удовлетворяющих данному условию, не существует.
Ответ: при n=4.
Эта задача могла быть сформулирована иначе:
Решить в целых числах уравнение 
Способ решения тот же. Только надо помнить, что по определению
Ответ: 
2. Решить в целых числах уравнение: 
Решение:
Так как
– произведение первых
натуральных чисел, значит,
, а целым может быть только k.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то

Но по свойству (1) квадрат целого числа не может оканчиваться ни 3, ни 8, значит, других целых решений уравнение не имеет.
Ответ: 
3. Решить в целых числах уравнение: 
Решение:
В решении этого уравнения надо использовать тот же приём, что и в предыдущих. Его легко решить устно.

Но тогдаоканчивается 8 или 3, а это противоречит свойству (1). Значит, при
уравнение не имеет решений в целых числах. Поэтому решения уравнения следует искать для

Если n=1, то
Если n=2, то.
Если n=3, то.
Если n=4, то.
Как видим, ни при какомчисло
не является точным квадратом.
Ответ: уравнение не имеет целых решений.
4. Решить уравнение в целых числах: 
Решение:


Значит,оканчивается 7, но тогда и
оканчивается 7.
Но квадрат целого числа не может оканчиваться 7, значит,целых решений нет.
Значит, решения уравнения следует искать при= 1, 2, 3, 4.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то
Ответ: 
5. Решить в натуральных числах уравнение 
Решение:
В этом уравнении 

Но квадрат целого числа не может оканчиваться 3, значит, принатуральных решений уравнение не имеет. Остаётся проверить наличие решений при
=1, 2, 3, 4.
Если n=1, то
Если n=2, то
Если n=3, то
Если n=4, то
Ответ:
6. Решить уравнение в целых числах: 1!+2!+3!+…+
Решение:
Если
=1, то 1! =
, тогда


Если=2, то 1!+2! =

– число не целое.
Если=3, то 1!+2!+3! =




Если=4, то 1!+2!+3!+4! =

– число не целое.
Если, то 1!+2!+3!+4!+…+х! оканчивается цифрой 3, но квадрат целого числа не может оканчиваться 3.
Значит, при
Ответ: 




7. Доказать, что уравнение 
Доказательство:
если
делится на 5, а это возможно, если
оканчивается 0 или 5, тогда

Но квадрат целого числа не может оканчиваться ни цифрой 3, ни цифрой 8.
Значит, уравнение не имеет целых решений. Что и требовалось доказать.
8. Решить в целых числах уравнение 
Решение:
Если n=1, то

Если n=2, то
Если n=3, то
Если n=4, то
Еслиуравнение целых решений не имеет, так как при чётном

1
2
3
4
…
(
1
2
3
4
…
(
=
=12
3
4
…
(

При нечётном
1
2
3
4
…
(
1
2
3
4
…
(
=1
2
3
4
…
(
– не делится на 4, а при делении на 8 даёт остаток 3, а не 1.
Ответ: 1)
9. Решить уравнение в целых числах: 
Решение:
Если
=1, то


Если=4, то

При(1
2
4
5
…
+1) =
– левая часть уравнения делится на 3, значит, число
должно делиться на 9.
Но1
2
4
5
…
+1 на 3 не делится, поэтому левая часть уравнения не кратна 9 Значит, при
уравнение не имеет целых решений.
Ответ: 1) 

10. Решить в целых числах уравнение:
Решение:

1) Если m – число чётное, то– числа нечётные и их произведение
– тоже число нечётное, но правая часть уравнения
– чётное число. Значит, при чётном m уравнение не имеет решений.
2) Если m – число нечётное, то– числа чётные, причем,
– два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда
, значит,
, но квадрат целого числа делится на 4 или при делении на 8 даёт остаток 1. А
лишь в единственном случае, если n=0. При n=0 уравнение примет вид:
Ответ: 
11. Решить в целых числах уравнение:
Решение:

1) Если n – число четное, то– числа нечётные, значит,
– тоже нечетное число, а это возможно лишь тогда, когда
, т.е.
. При всех других чётных
уравнение целых решений не имеет.
2) Если n – число нечётное, то – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда их произведение. Значит, и левая часть уравнения
, но
– число нечётное, значит, только
. Это возможно, если
. При
.
При,
.
Если же, то
, а правая часть уравнения
, значит, других решений уравнение не имеет.
Ответ: 1) 
12. Решить в целых числах уравнение:
Решение:
– имеет решение, если:
1)= 0, тогда

— число нечётное,
. Тогда,
,

.
() – нечётное число при
. Значит,
тоже должно быть нечётным, а это возможно, если
. Тогда при
исходное уравнение примет вид
.
Ответ: 1) 
13. Доказать, что число, оканчивающееся двумя одинаковыми цифрами, отличными от 0 и 4, не может быть точным квадратом.
Доказательство:
Так как квадрат любого числа может оканчиваться цифрами: 0; 1; 4; 5; 6; 9, то кроме 0 и 4 последними цифрами могут быть: 11; 55; 66; 99.

— число чётное, тогда
.

Значит, не существует таких чисел, что
оканчивается 55, 66, 11 или 99.
Что и требовалось доказать.
14. Доказать, что тысячезначное число, все цифры которого пятёрки, за исключением, быть может, одной, не является точным квадратом.
Доказательство:
а) Если число оканчивается 5, то предпоследняя цифра может быть только 2, тогда 55….525 – число нечётное, оно не кратно 4, значит, при делении на 8 должно дать в остатке 1, но
. Значит, число не может быть точным квадратом.
б) Если последняя цифра не 5, то это может быть 0; 1; 4; 6; 9, тогда
– не может быть, т.к.
оканчиваться чётным числом нулей.
– не может быть, т.к.
.
– чётно, но не кратно 4, т.к. 54 не делится на 4.
– нечётное, но при делении на 8 даёт остаток 7, а не 1.
– чётно и делится нацело на 4, но не всякое чётное число, кратное 4, является точным квадратом. Проверим, выполняется ли свойство (3) квадрата целого числа.
сумма цифр
не делится на 9, а при делении на 3 в остатке 0.
Таким образом, ни одно из перечисленных чисел не может быть точным квадратом. Что и требовалось доказать.



 2
2 3
3 4
4 5
5 6
6 …
… n – произведение первых n натуральных чисел.
n – произведение первых n натуральных чисел.  2 = 2
2 = 2  2
2 3 = 6
3 = 6  2
2 3
3 4 = 24
4 = 24  2
2 3
3 4
4 5 = 120
5 = 120  2
2 3
3 4
4 5
5 6 = 720 и т.д.
6 = 720 и т.д. – не является точным квадратом.
– не является точным квадратом.  – не является точным квадратом.
– не является точным квадратом.  – не является точным квадратом.
– не является точным квадратом.  , значит, при n=4 число
, значит, при n=4 число  является точным квадратом числа.
является точным квадратом числа.  , то
, то  оканчивается 0, тогда
оканчивается 0, тогда  оканчивается 7, но по свойству (1) квадрат целого числа не может оканчиваться цифрой 7. Значит, других натуральных чисел n, удовлетворяющих данному условию, не существует.
оканчивается 7, но по свойству (1) квадрат целого числа не может оканчиваться цифрой 7. Значит, других натуральных чисел n, удовлетворяющих данному условию, не существует.
 – произведение первых
– произведение первых  натуральных чисел, значит,
натуральных чисел, значит,  , а целым может быть только k.
, а целым может быть только k. 





 оканчивается 8 или 3, а это противоречит свойству (1). Значит, при
оканчивается 8 или 3, а это противоречит свойству (1). Значит, при  уравнение не имеет решений в целых числах. Поэтому решения уравнения следует искать для
уравнение не имеет решений в целых числах. Поэтому решения уравнения следует искать для 

 .
.  .
.  .
.  число
число  не является точным квадратом.
не является точным квадратом.
 оканчивается 7, но тогда и
оканчивается 7, но тогда и  оканчивается 7.
оканчивается 7.  целых решений нет.
целых решений нет.  = 1, 2, 3, 4.
= 1, 2, 3, 4. 




 натуральных решений уравнение не имеет. Остаётся проверить наличие решений при
натуральных решений уравнение не имеет. Остаётся проверить наличие решений при  =1, 2, 3, 4.
=1, 2, 3, 4. 





 =1, то 1! =
=1, то 1! = , тогда
, тогда 

 =2, то 1!+2! =
=2, то 1!+2! = 
 – число не целое.
– число не целое.  =3, то 1!+2!+3! =
=3, то 1!+2!+3! = 



 =4, то 1!+2!+3!+4! =
=4, то 1!+2!+3!+4! = 
 – число не целое.
– число не целое.  , то 1!+2!+3!+4!+…+х! оканчивается цифрой 3, но квадрат целого числа не может оканчиваться 3.
, то 1!+2!+3!+4!+…+х! оканчивается цифрой 3, но квадрат целого числа не может оканчиваться 3. 


 если
если  делится на 5, а это возможно, если
делится на 5, а это возможно, если  оканчивается 0 или 5, тогда
оканчивается 0 или 5, тогда 




 уравнение целых решений не имеет, так как при чётном
уравнение целых решений не имеет, так как при чётном 
 1
1 2
2 3
3 4
4 …
…  (
( 1
1 2
2 3
3 4
4 …
…  (
(  =
=  2
2 3
3 4
4 …
…  (
( 

 1
1 2
2 3
3 4
4 …
…  (
( 1
1 2
2 3
3 4
4 …
…  (
(  =1
=1 2
2 3
3 4
4 …
…  (
(  – не делится на 4, а при делении на 8 даёт остаток 3, а не 1.
– не делится на 4, а при делении на 8 даёт остаток 3, а не 1.
 =1, то
=1, то 

 =4, то
=4, то 
 (1
(1 2
2 4
4 5
5 …
…  +1) =
+1) =  – левая часть уравнения делится на 3, значит, число
– левая часть уравнения делится на 3, значит, число  должно делиться на 9.
должно делиться на 9.  1
1 2
2 4
4 5
5 …
…  +1 на 3 не делится, поэтому левая часть уравнения не кратна 9 Значит, при
+1 на 3 не делится, поэтому левая часть уравнения не кратна 9 Значит, при  уравнение не имеет целых решений.
уравнение не имеет целых решений.


 – числа нечётные и их произведение
– числа нечётные и их произведение  – тоже число нечётное, но правая часть уравнения
– тоже число нечётное, но правая часть уравнения  – чётное число. Значит, при чётном m уравнение не имеет решений.
– чётное число. Значит, при чётном m уравнение не имеет решений.  – числа чётные, причем,
– числа чётные, причем,  – два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда
– два последовательных чётных числа, одно из которых кратно 2, а другое – 4. Тогда  , значит,
, значит,  , но квадрат целого числа делится на 4 или при делении на 8 даёт остаток 1. А
, но квадрат целого числа делится на 4 или при делении на 8 даёт остаток 1. А  лишь в единственном случае, если n=0. При n=0 уравнение примет вид:
лишь в единственном случае, если n=0. При n=0 уравнение примет вид: 


 – числа нечётные, значит,
– числа нечётные, значит,  – тоже нечетное число, а это возможно лишь тогда, когда
– тоже нечетное число, а это возможно лишь тогда, когда  , т.е.
, т.е.  . При всех других чётных
. При всех других чётных  уравнение целых решений не имеет.
уравнение целых решений не имеет.  . Значит, и левая часть уравнения
. Значит, и левая часть уравнения  , но
, но  – число нечётное, значит, только
– число нечётное, значит, только  . Это возможно, если
. Это возможно, если  . При
. При 
 .
. 
 ,
,  .
.  , то
, то 
 , а правая часть уравнения
, а правая часть уравнения  , значит, других решений уравнение не имеет.
, значит, других решений уравнение не имеет.

 – имеет решение, если:
– имеет решение, если:  = 0, тогда
= 0, тогда 
 — число нечётное,
— число нечётное,  . Тогда,
. Тогда,  ,
, 
 .
.  ) – нечётное число при
) – нечётное число при  . Значит,
. Значит,  тоже должно быть нечётным, а это возможно, если
тоже должно быть нечётным, а это возможно, если  . Тогда при
. Тогда при  исходное уравнение примет вид
исходное уравнение примет вид  .
.


 — число чётное, тогда
— число чётное, тогда  .
. 
 , что
, что  оканчивается 55, 66, 11 или 99.
оканчивается 55, 66, 11 или 99. . Значит, число не может быть точным квадратом.
. Значит, число не может быть точным квадратом.  – не может быть, т.к.
– не может быть, т.к.  оканчиваться чётным числом нулей.
оканчиваться чётным числом нулей.  – не может быть, т.к.
– не может быть, т.к.  .
.  – чётно, но не кратно 4, т.к. 54 не делится на 4.
– чётно, но не кратно 4, т.к. 54 не делится на 4.  – нечётное, но при делении на 8 даёт остаток 7, а не 1.
– нечётное, но при делении на 8 даёт остаток 7, а не 1.  – чётно и делится нацело на 4, но не всякое чётное число, кратное 4, является точным квадратом. Проверим, выполняется ли свойство (3) квадрата целого числа.
– чётно и делится нацело на 4, но не всякое чётное число, кратное 4, является точным квадратом. Проверим, выполняется ли свойство (3) квадрата целого числа.  сумма цифр
сумма цифр  не делится на 9, а при делении на 3 в остатке 0.
не делится на 9, а при делении на 3 в остатке 0.